Suites numériques

Suites Numériques

1 p 14

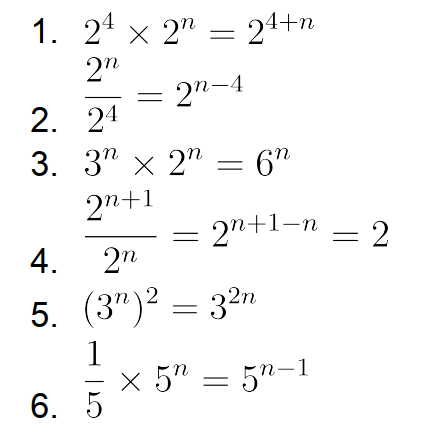
2 p 14

0,99^6\approx 0,9415

\text{CM }= 1+t\text{ donc }t = \text{ CM}-1

0,9415-1 = -0,0585

donc le taux global est égal $-5,85$%.

3 p 14

4 p 14

h(1)=\dfrac{1}{1}=1~;~h(2)=\dfrac{1}{2}=0,5~;~h(3)=\dfrac{1}{3}~;~h(4)=\dfrac{1}{4}=0,25~;~

h(5)=\dfrac{1}{5}=0,2

n>0\text{ et }n+1>0\text{ donc }U(n)<0

On observe que la suite de nombres est décroissante si

h(n+1)-h(n)<0.

5 p 14

\text{1) } 7+0,5 \times 1 = 7,5

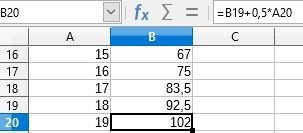
Le nombre affiché dans la cellule B2 sera donc 7,5.

2) La cellule B20 contiendra la formule = B19 + 0,5*A20

6 p 14

L'algorithme affecte successivement à la variable U les nombres 1, 3, 5... 17, 19.

Question supplémentaire : Traduire l'algorithme en Python avec en plus un affichage des nombres précédents.

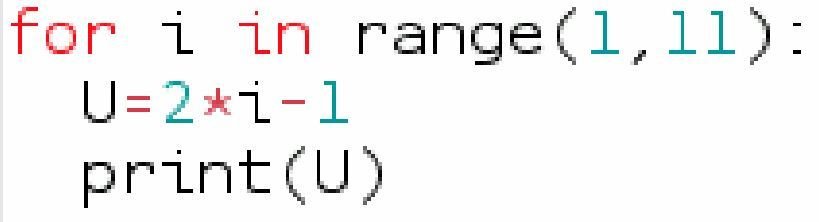
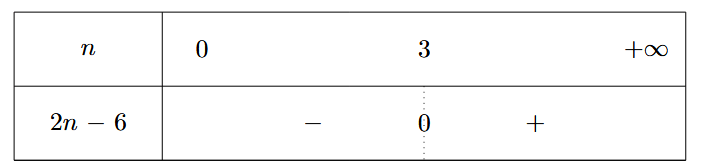
7 p 14

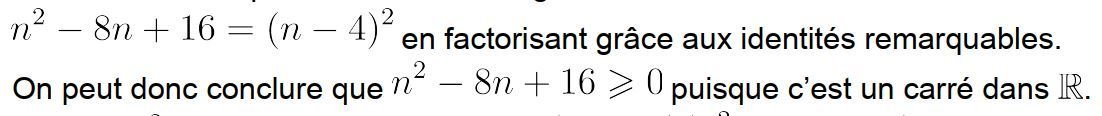
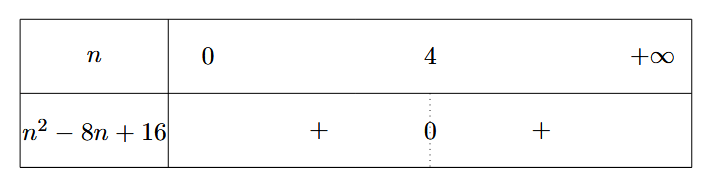
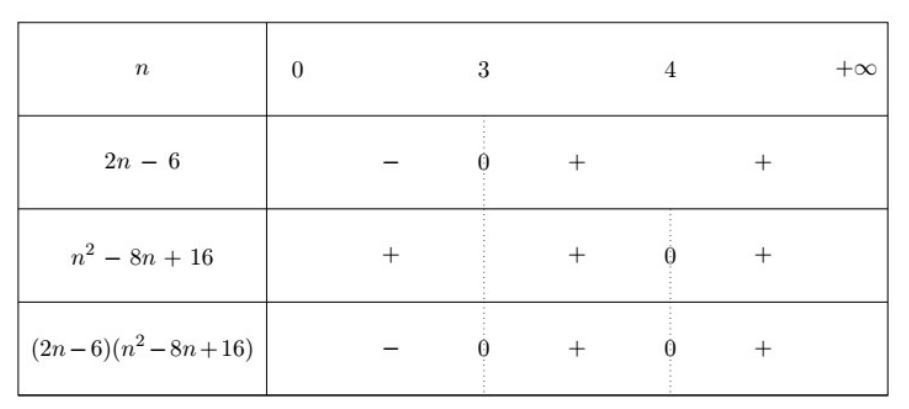
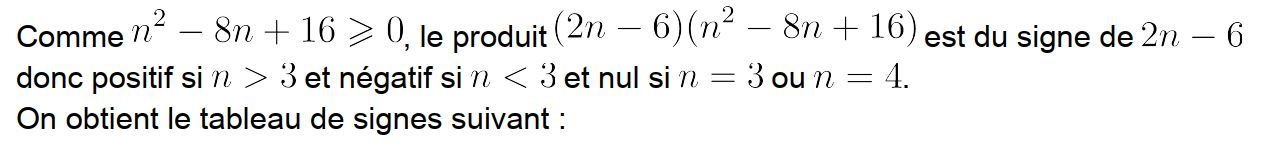
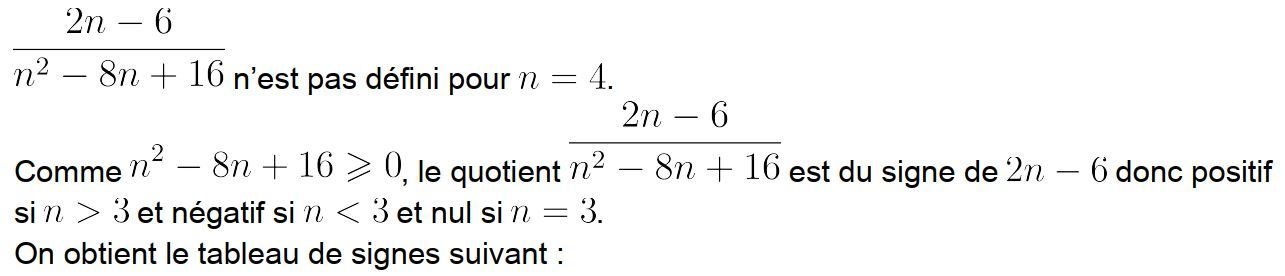
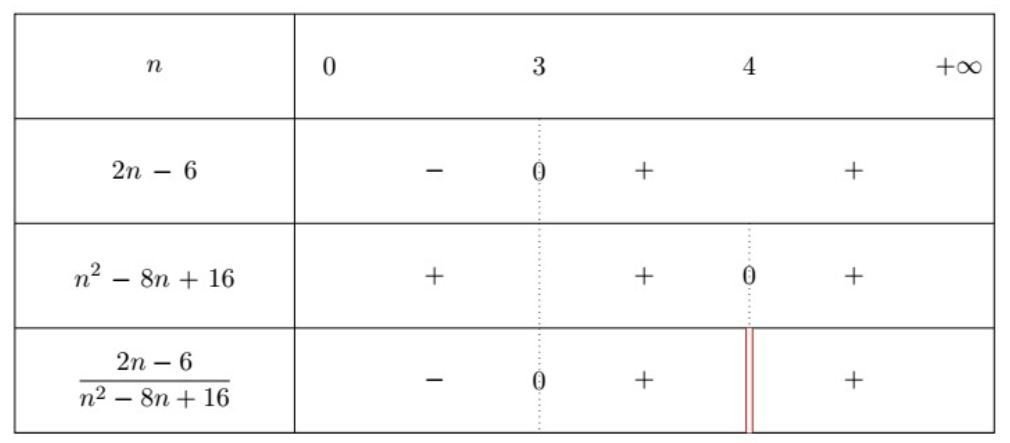
8 p 14

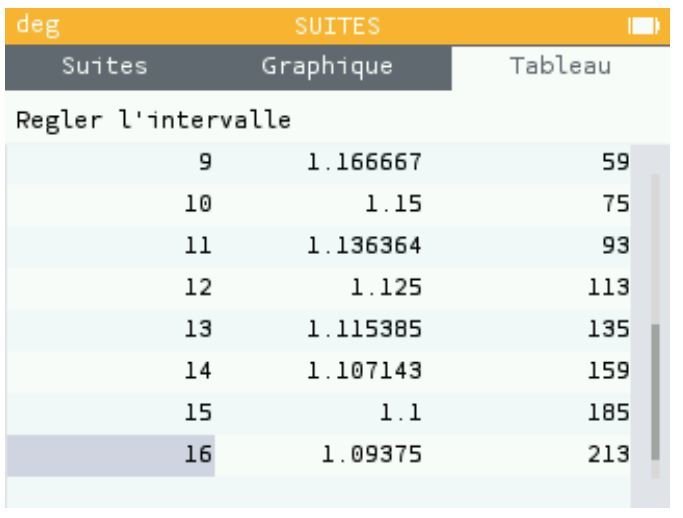
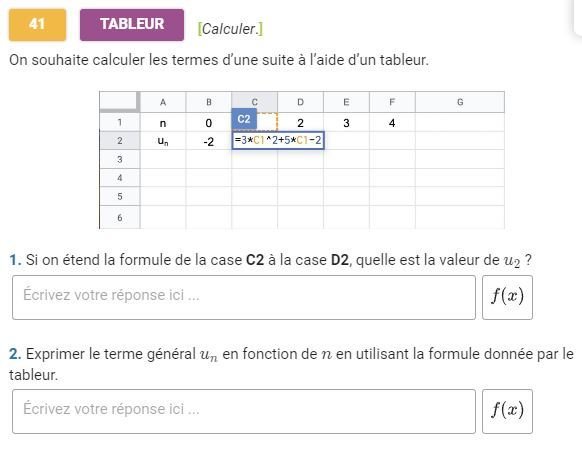
On souhaite introduire la notion de suite à l’aide d’un tableur afin de pouvoir trouver une expression du terme général en fonction de $n .$ On considère la feuille de calcul suivante.

Act A p 16 : Soyons explicite

22 p 31

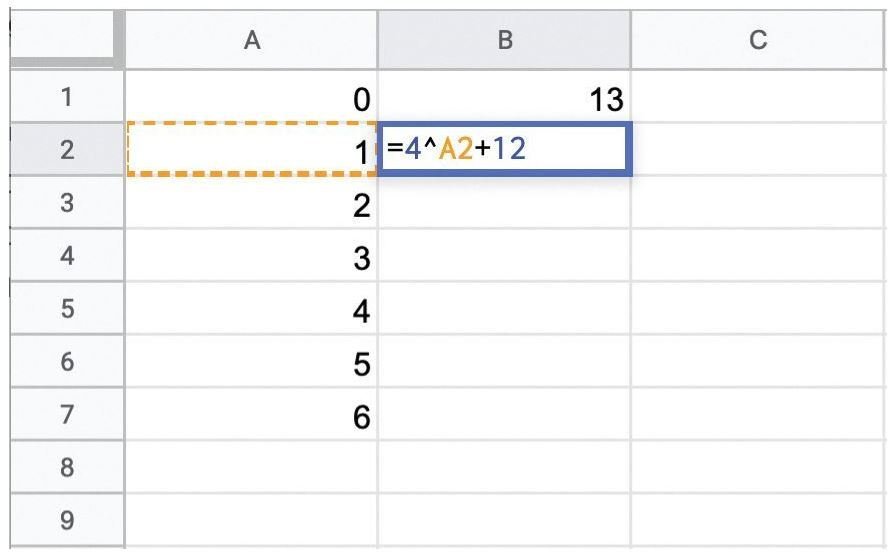
u_{n+1}=\dfrac{3^{n+1+1}}{2^{n+1}}=\dfrac{3^{n+2}}{2^{n+1}}

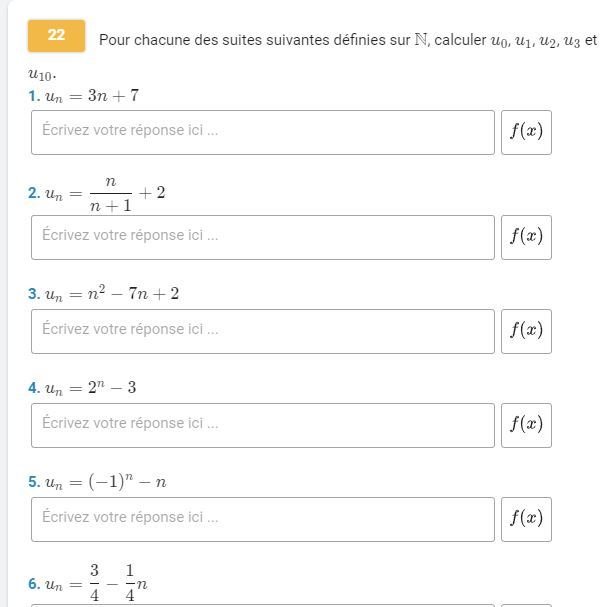
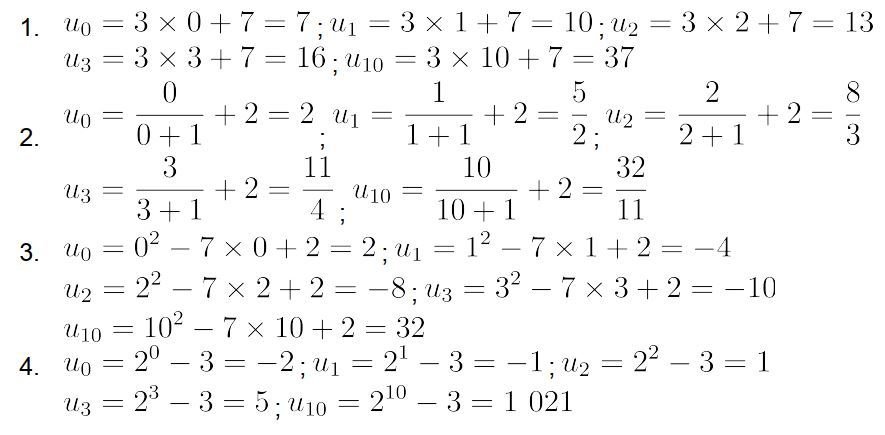
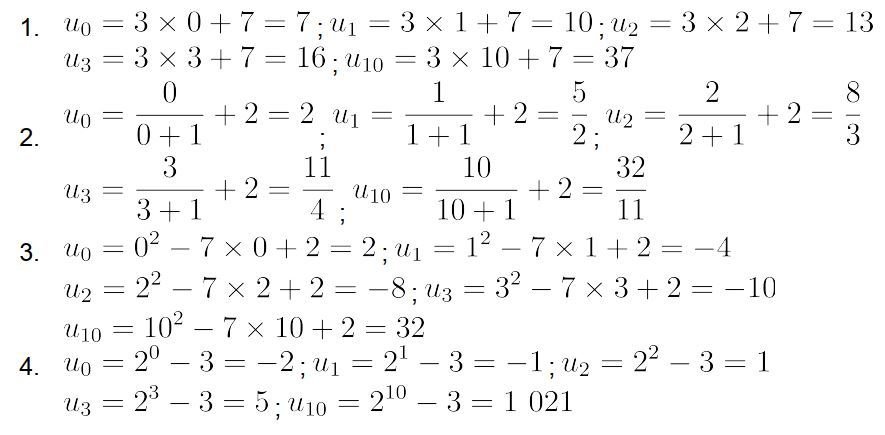
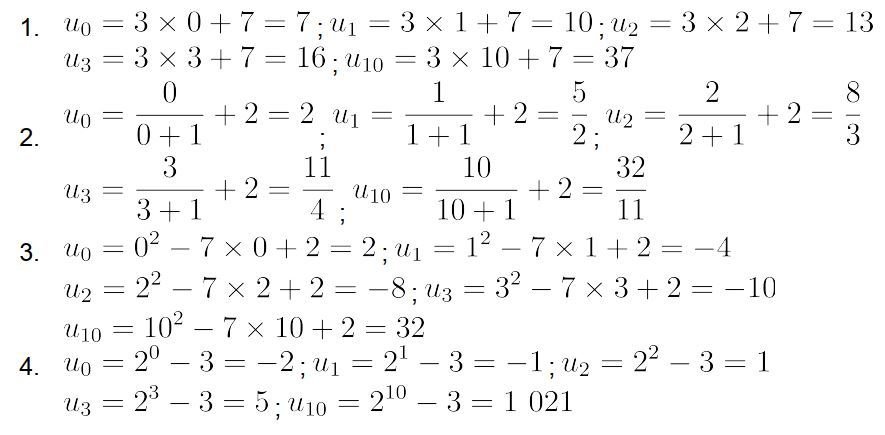
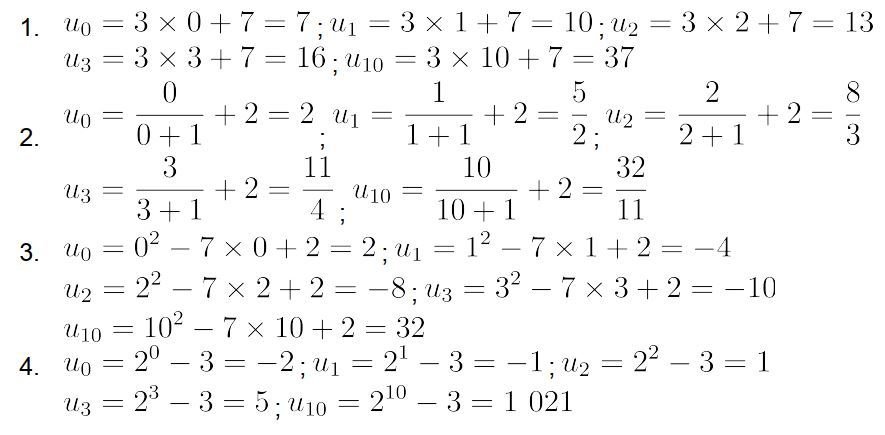
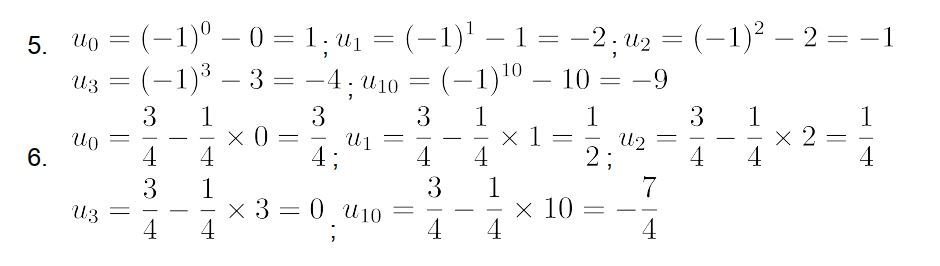
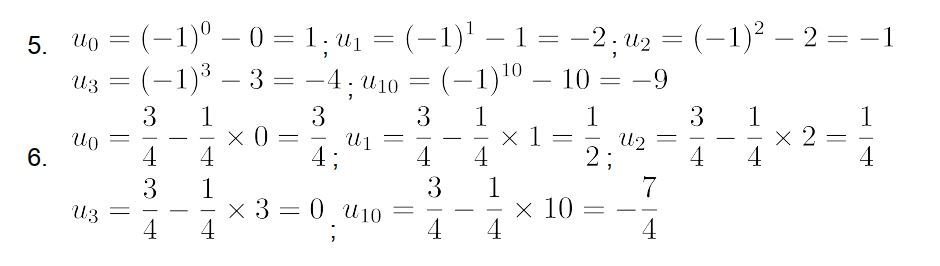
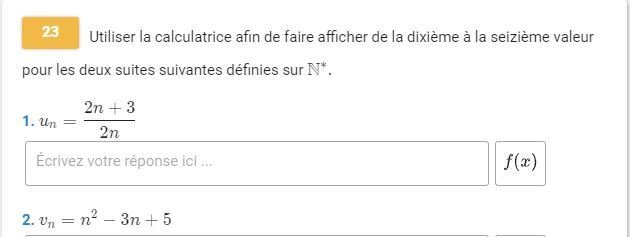
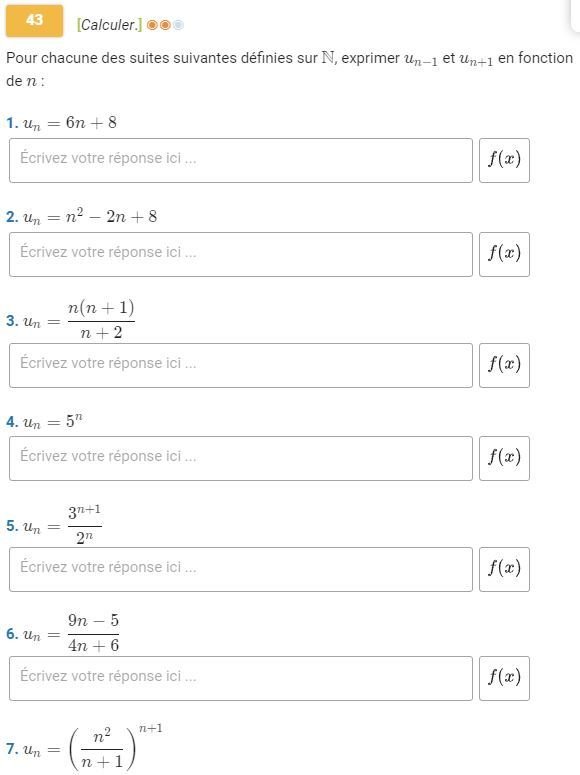
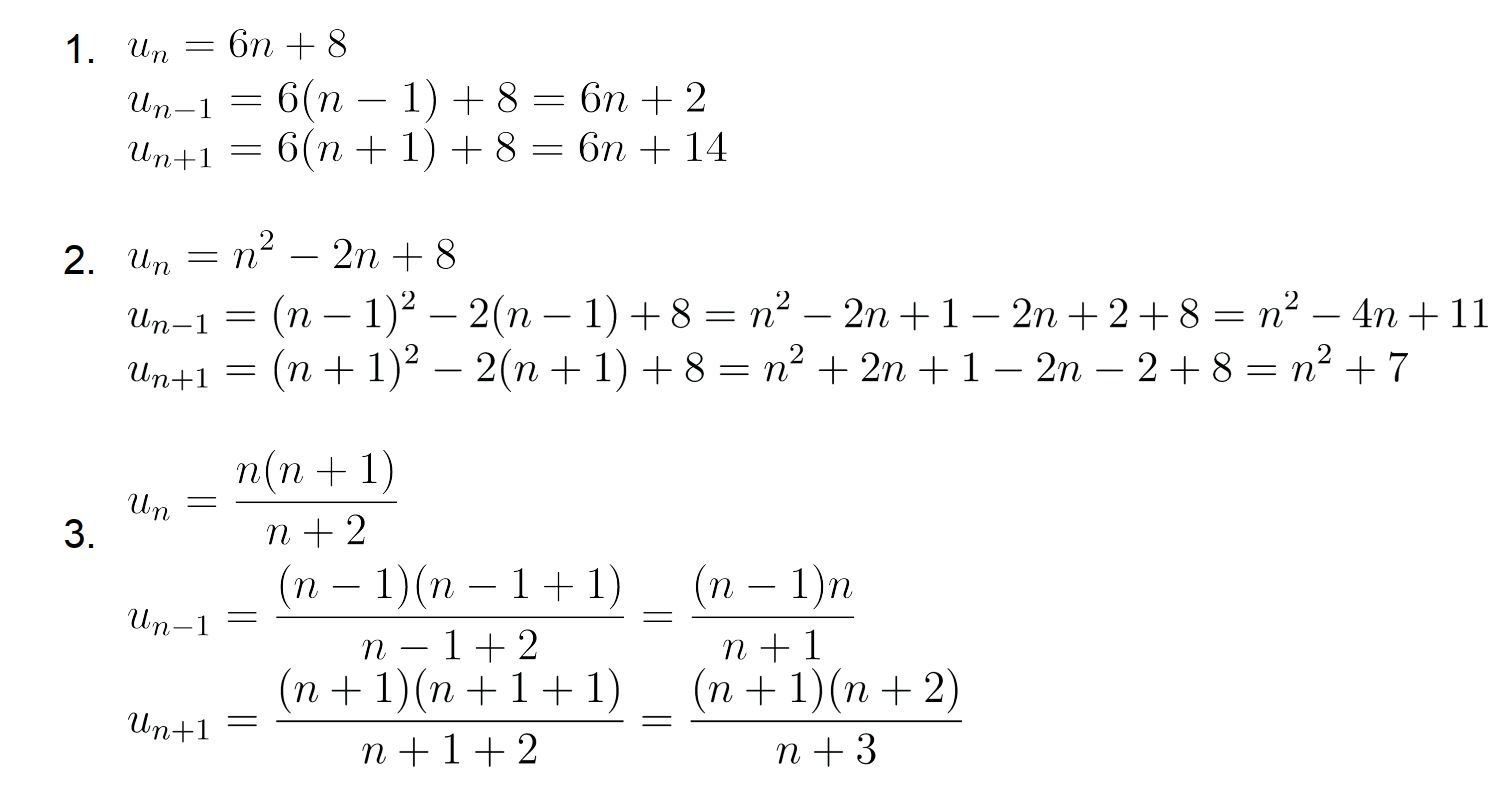
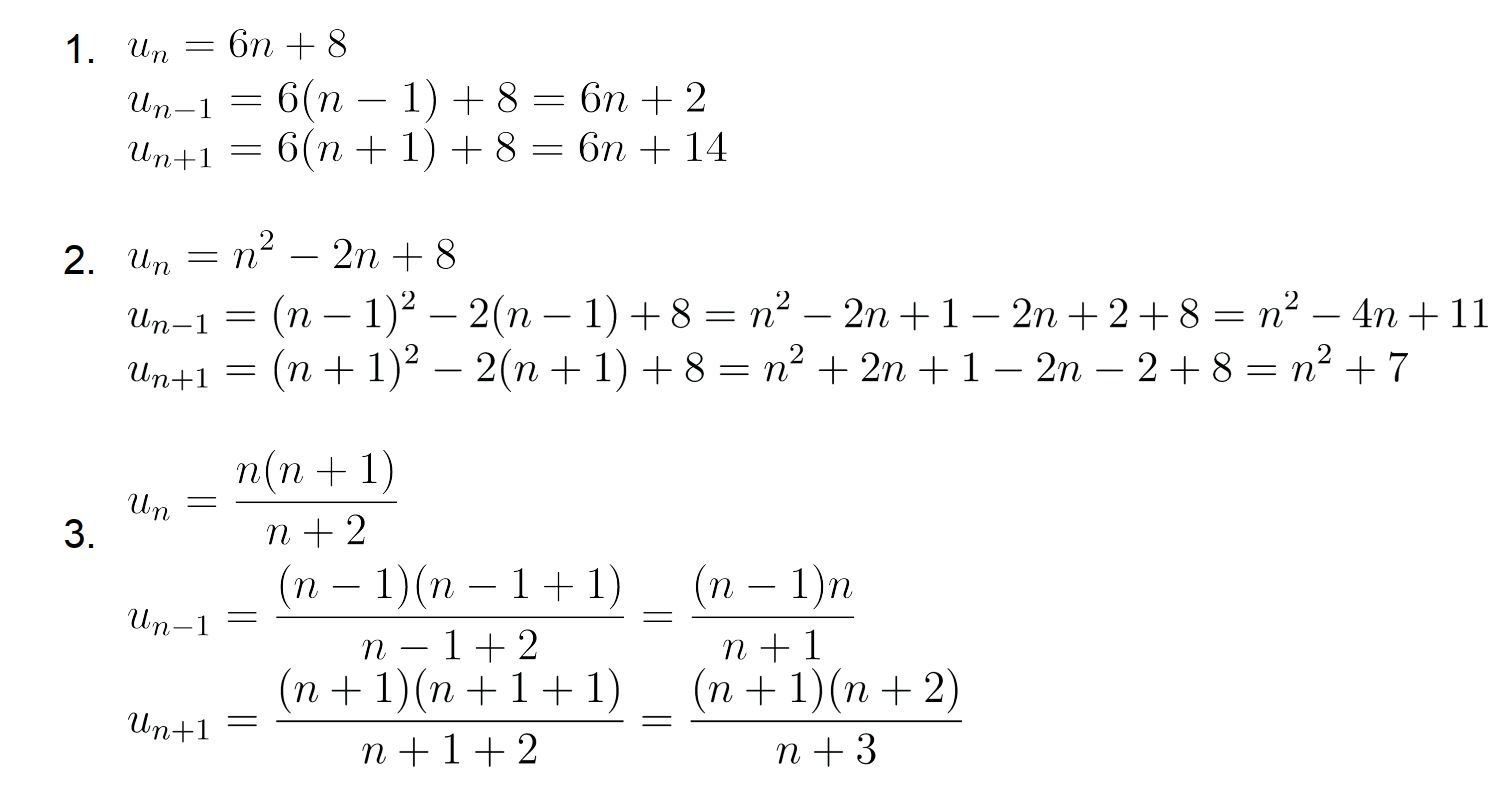
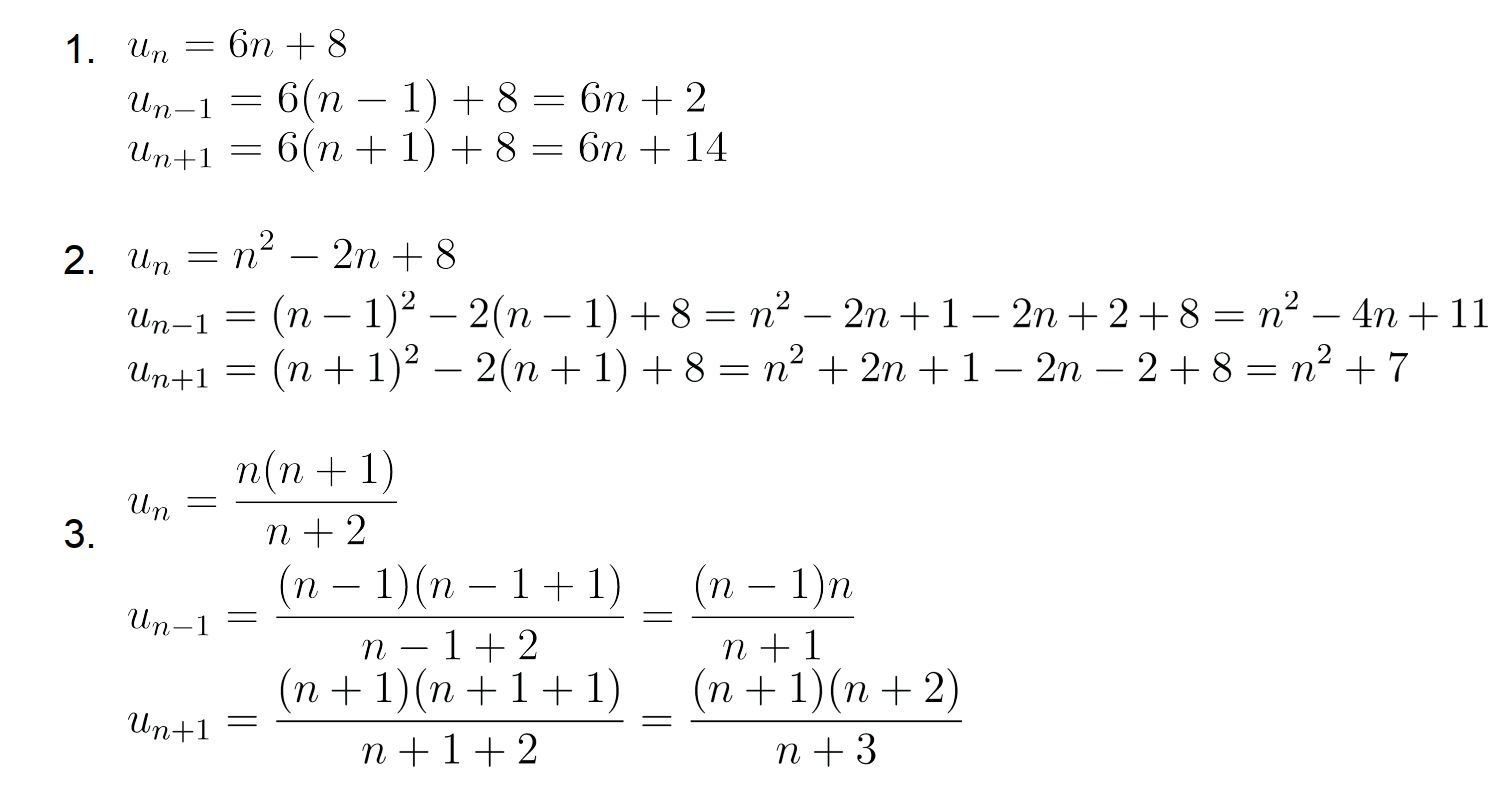
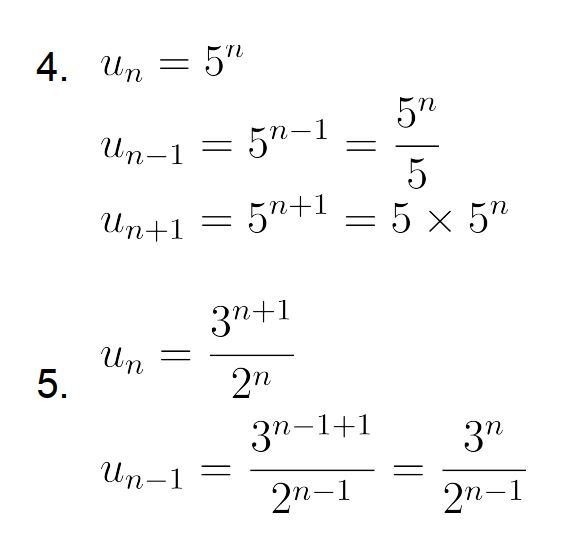
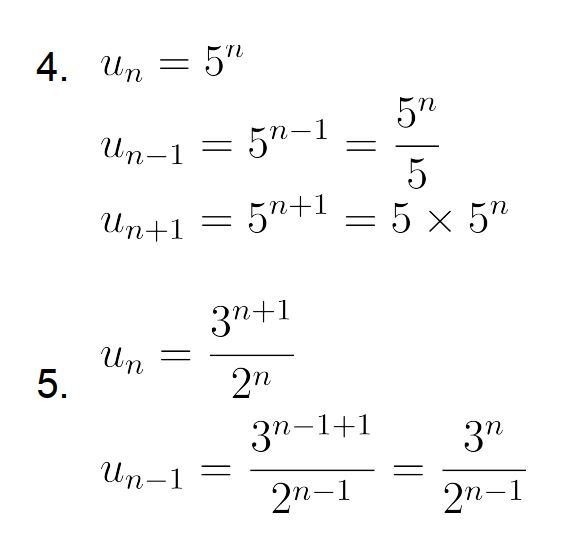
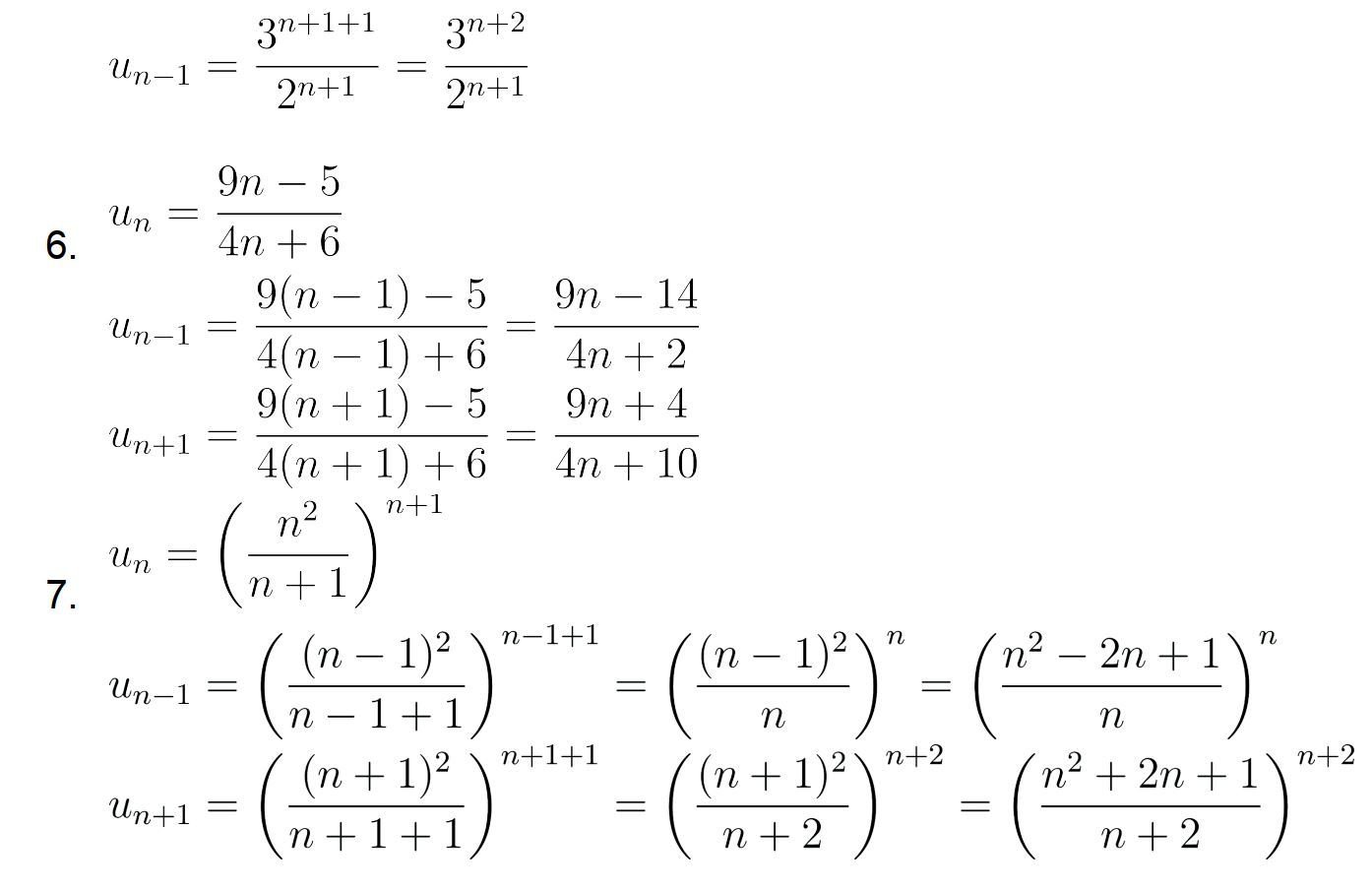
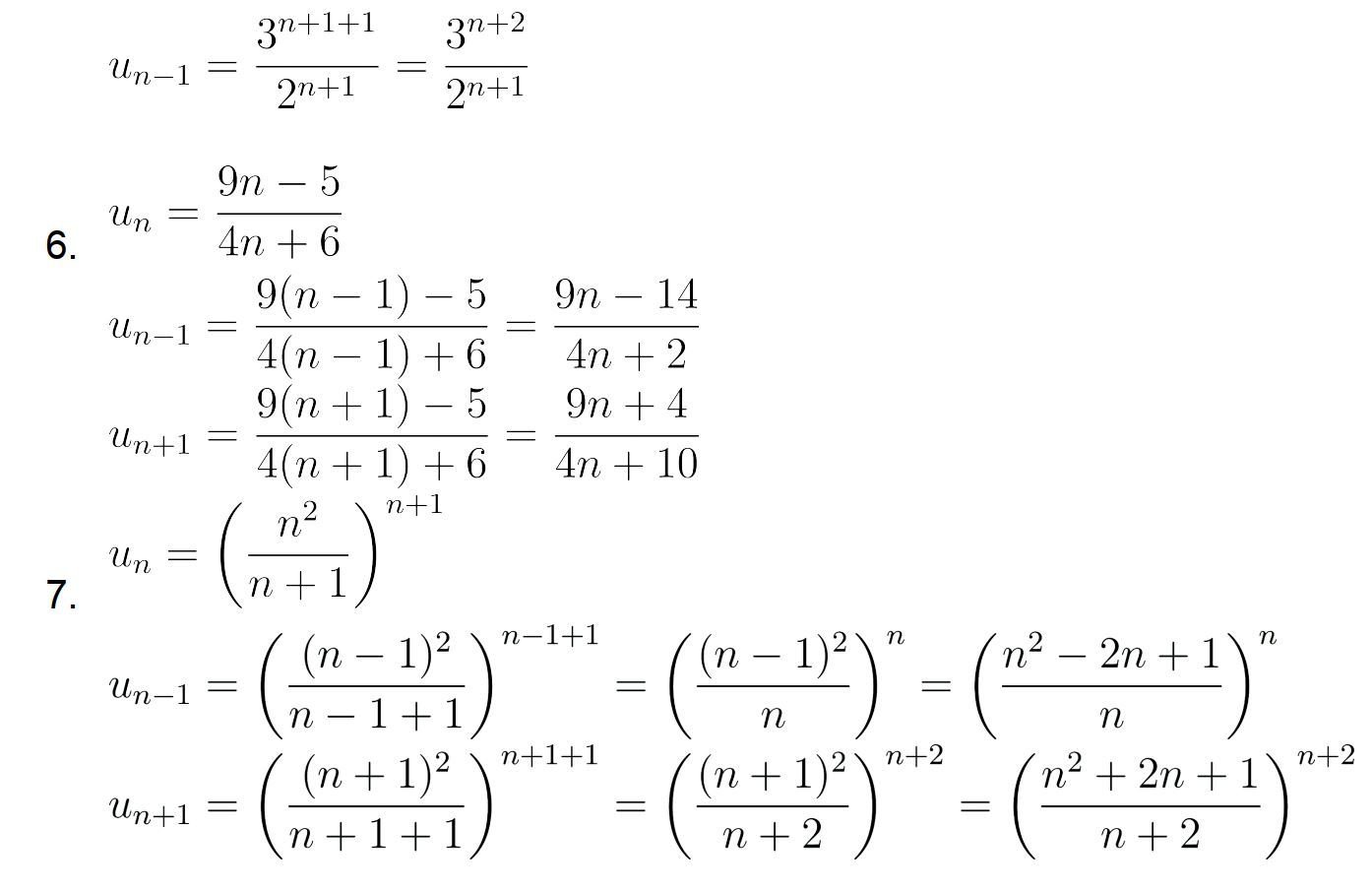
Activité B p 16 : Suite définie par une relation de récurrence

\text{EX0 : On considère la suite } (u_n) \text{ définie par : }

u_0= 3 \text{ et } u_{n+1}=4u_n-1.

\text{Calculer }u_1, u_2 \text{ et }u_3.

u_{1}=4u_0-1=4\times 3-1 = 11

u_{2}=4u_1-1=4\times 11-1 = 43

u_{3}=4u_2-1=4\times 43-1 = 171

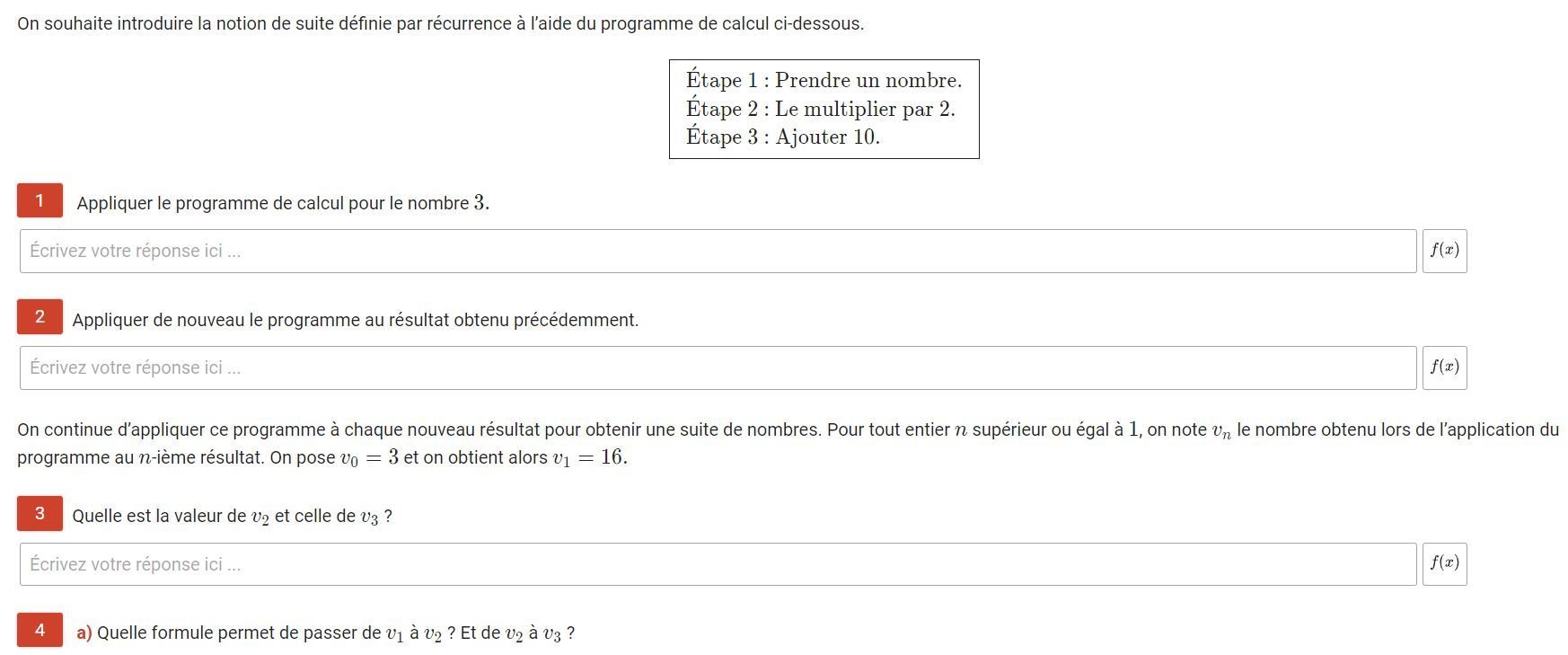
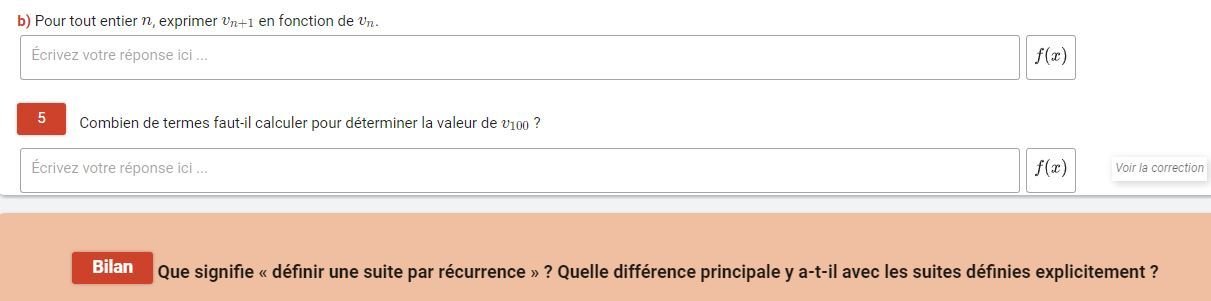
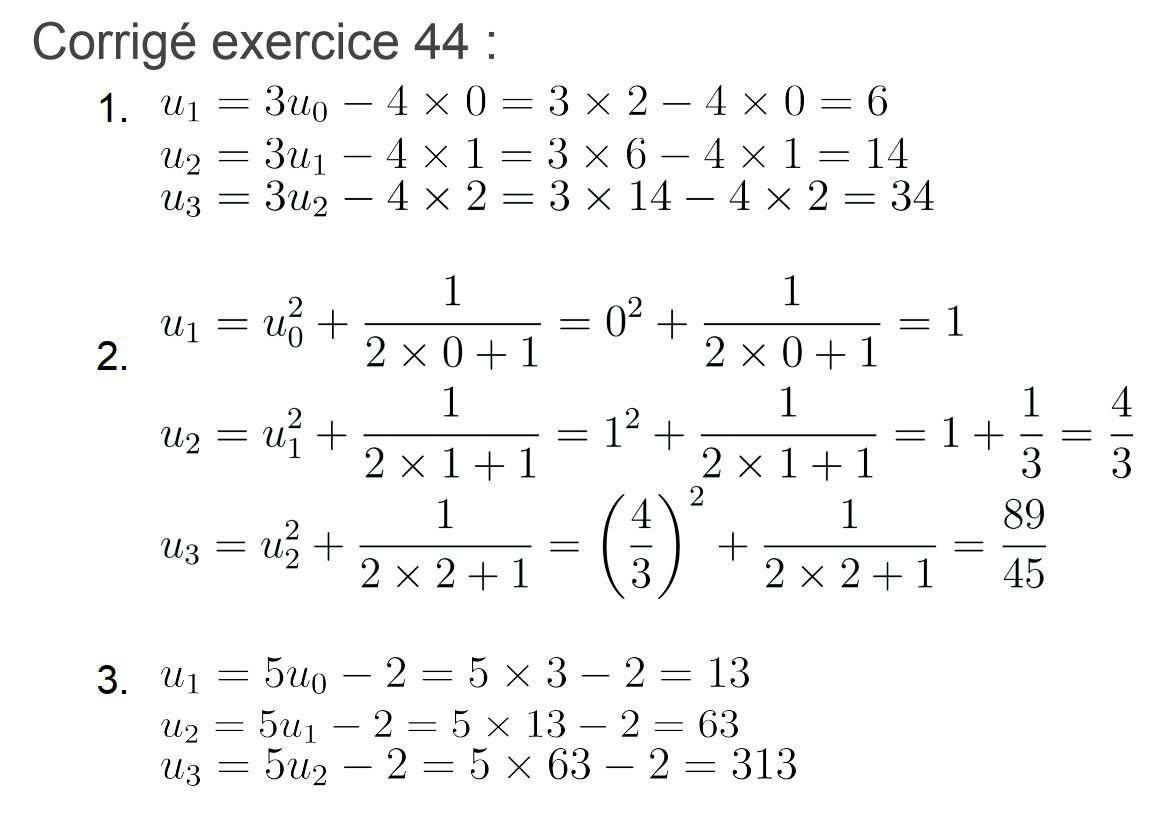
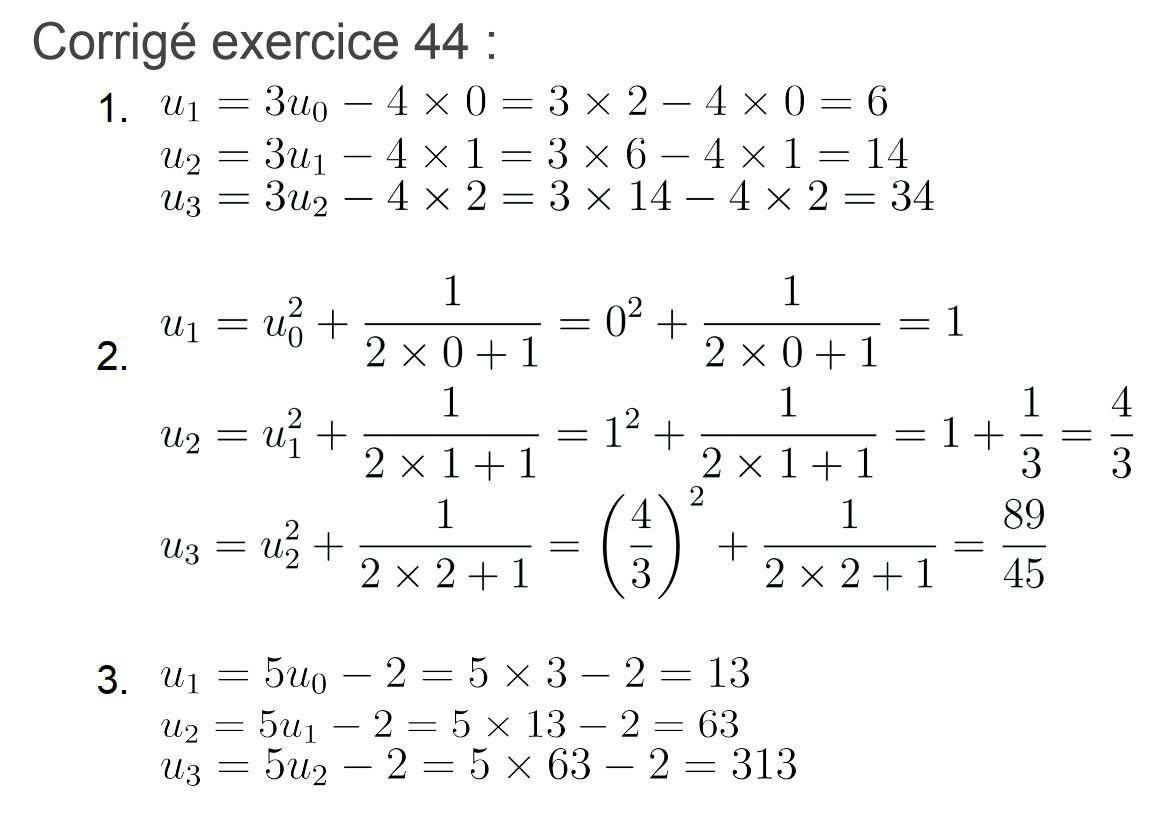
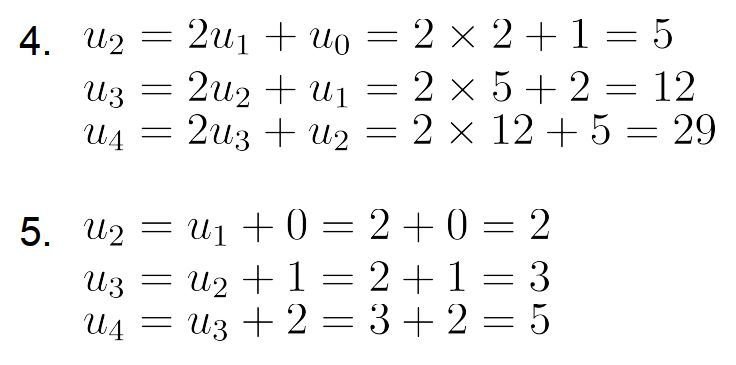
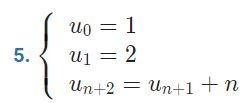
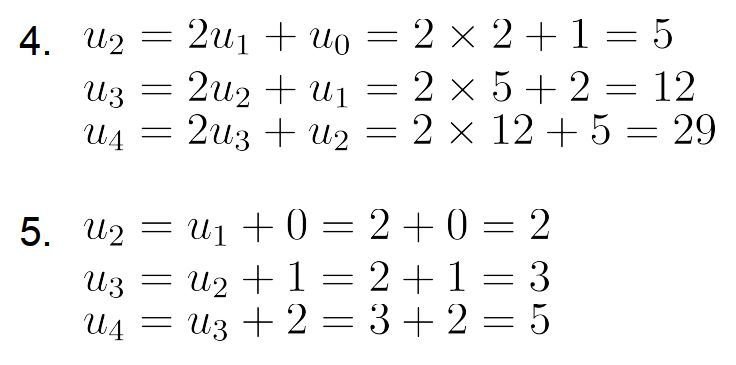
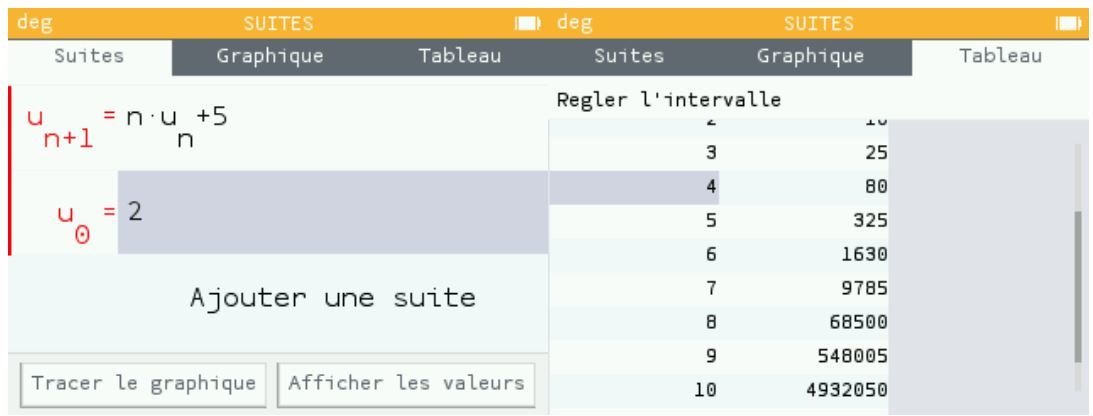
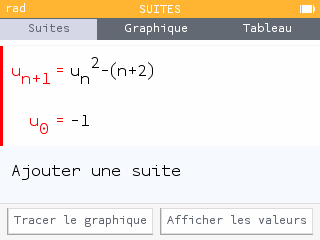
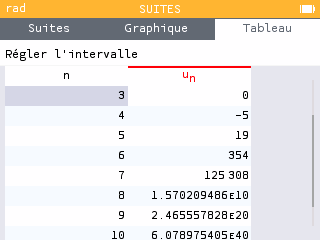
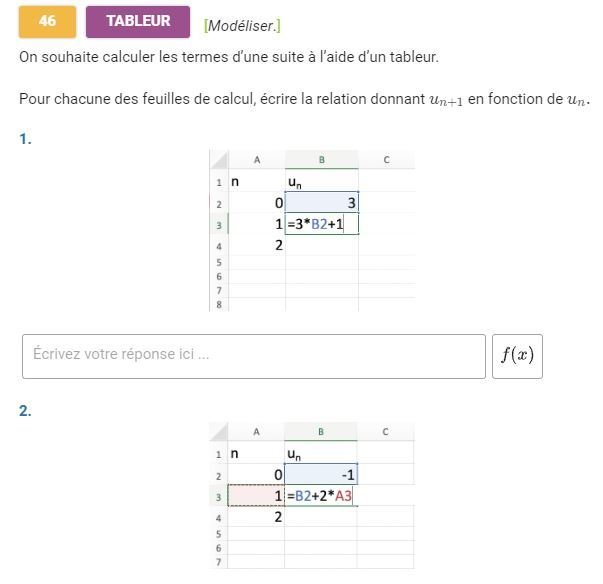
(préciser en plus le premier terme de la suite)

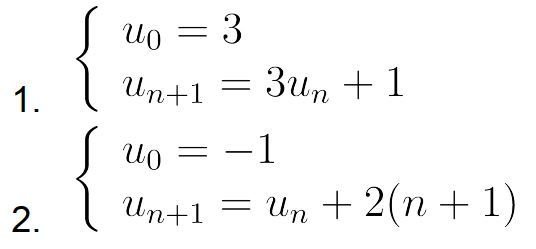
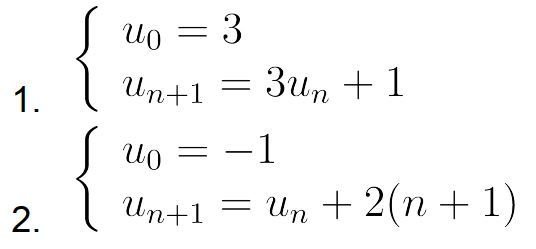
Les termes de u1 à u10 d'une suite définie par récurrence dont le premier terme est u0 = 1.

u_{n+1}=\dfrac{u_n-1}{ u_n-2}.

Question supplémentaire : Programmer l'algorithme en Python avec affichage de $u_{10}$

Programmation de l'algorithme en Python :

u \leftarrow 1 \\ pour \;i\leftarrow1\;à\;10\;faire \\ u\leftarrow\dfrac{u-1}{u-2}\\ fin

u = 1
for i in range(10):
    u = (u-1)/(u-2)
print(u)

(on affiche uniquement u10)

u_{10}\approx 0,382.

Le programme affiche

Vérification avec le mode suite de la calculatrice :

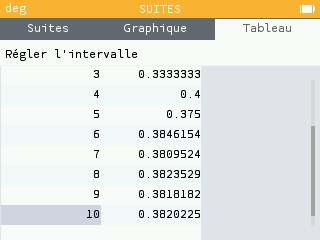
Variations d'une suite

*\; \text{Etudier le signe de }u_{n+1}-u_n .

*\; \text{Comparer }\dfrac{u_{n+1}}{u_n} \text{ à 1}

\text{(pour les suites strictement positives)}.

*\; \text{Si }u_{n}=f(n) \text{, on peut utiliser les variations de}f.

u_{n+1}-u_n=-(n-4)^2

\text{Pour tout }n\in\N,u_{n+1}-u_n\leqslant0 \text{ donc la suite }(u_n) \text{ est décroissante.}

\text{Pour tout entier naturel }n,(n-4)^2\geqslant0 \text{ donc }-(n-4)^2\leqslant0.

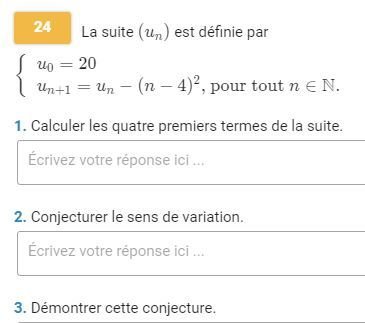
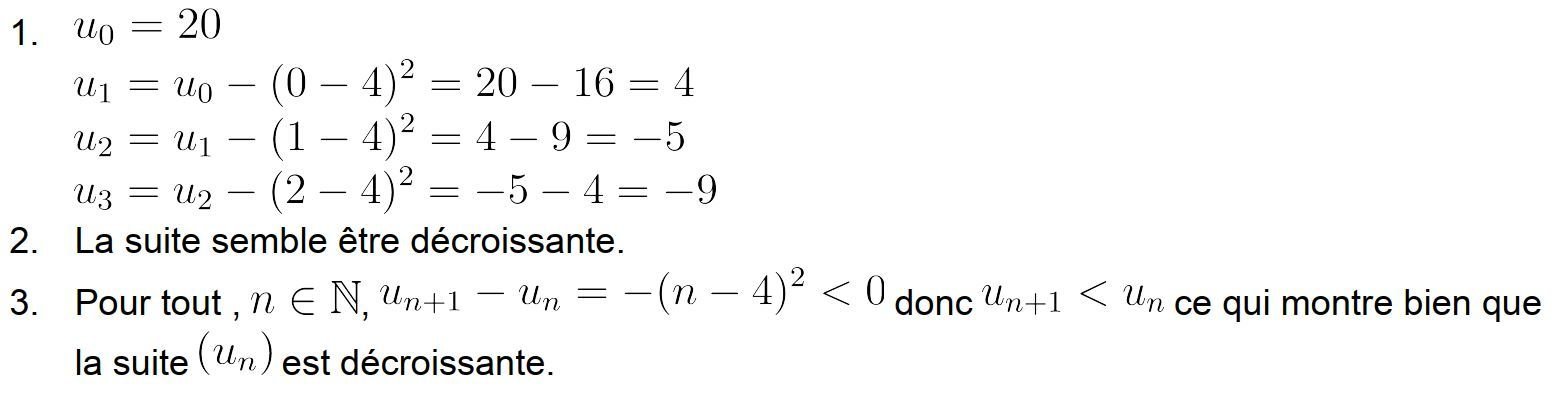
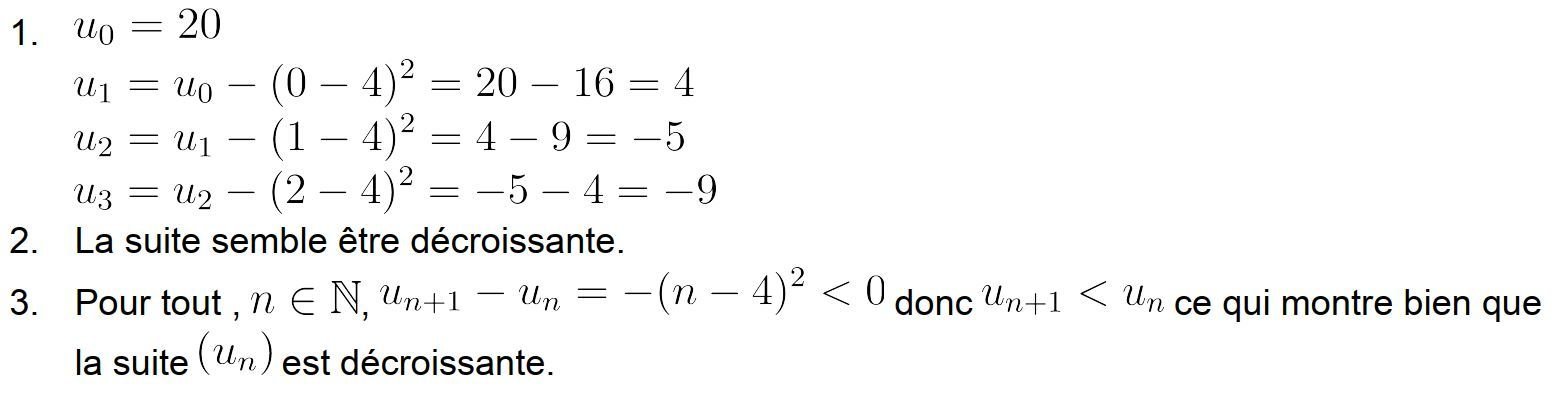
Ex 49 p 33 : Dans chaque cas, déterminer le sens de variation de la suite (un) définie par :

a.\;u_n=\frac{n+1}{n+2}\;pour\;tout\; n\in\mathbb{N}.

\text{On a }u_{n+1}=\frac{n+2}{n+3}.

u_{n+1}-u_n=\frac{n+2}{n+3}-\frac{n+1}{n+2}

Donc

=\frac{(n+2)^2-(n+1)(n+3)}{(n+3)(n+2)}

=\frac{n^2+4n+4-(n^2+4n+3)}{(n+3)(n+2)}

=\frac{1}{(n+3)(n+2)}

n+3>0\;et\;n+2>0.

Donc pour tout entier naturel $n$,

u_{n+1}-u_n > 0.

On en déduit que la suite (un) est strictement croissante.

https://colab.research.google.com/drive/12roRCPe0poyDFOMLsn0GzB6jOA39bS6G

Représentation graphique :

b.\;u_n=\frac{3^n}{n}\;pour\;tout\; n\geqslant1.

\text{On a }u_{n+1}=\frac{3^{n+1}}{n+1}.

u_{n+1}-u_n=\dfrac{3^{n+1}}{n+1}-\dfrac{3^n}{n}

Méthode 1 :

=\frac{3^{n+1}\times n }{n(n+1)}-\frac{3^{n}(n+1) }{n(n+1)}

=\frac{3^{n}\times 3n -3^{n}(n+1)}{n(n+1)}

=\frac{3^{n+1}\times n }{n(n+1)}-\frac{3^{n}(n+1) }{n(n+1)}

=\frac{3^{n+1}\times n -3^{n}(n+1)}{n(n+1)}

u_{n+1}-u_n=\frac{3^{n}(3n -(n+1))}{n(n+1)}

=\frac{3^{n}(3n -n-1)}{n(n+1)}

=\frac{3^{n}(2n -1)}{n(n+1)}

3^n>0\text{ et }n(n+1)>0.

\text{ On sait que }n\geqslant 1 \text{ donc }2n\geqslant 2 \text{ d'où }2n-1\geqslant 1.

Donc pour tout entier naturel $n$,

u_{n+1}-u_n > 0.

On en déduit que la suite (un) est strictement croissante.

\text{donc }\dfrac{3n}{n+1}>1.

donc la suite (un) est strictement croissante.

b.\;u_n=\frac{3^n}{n}\;pour\;tout\; n\geqslant1.

\text{On a }u_{n+1}=\frac{3^{n+1}}{n+1}.

Les termes de la suite (un) sont strictement positifs donc on peut comparer

\dfrac{u_{n+1}}{u_n}\;à\;1.

\dfrac{u_{n+1}}{u_n}=\dfrac{\frac{3^{n+1}}{n+1}}{\frac{3^n}{n}}=\frac{3^{n+1}}{n+1}\times \frac{n}{3^n}=\frac{3n}{n+1}

n\geqslant1\text{ donc }n+n\geqslant n+1\Leftrightarrow2n\geqslant n+1.

\text{Si }n\geqslant1\text{ alors } 3n>2n.\text{ On en déduit que } 3n>n+1

\text{Pour tout }n\in \N,\dfrac{u_{n+1}}{u_n}>1

Méthode 2 :

Par conséquent la suite (un) est croissante à partir de n = 1.

c.\;u_n=n^2-3n+12\;pour\;tout\; n\in\mathbb{N}.

On \;a\;u_{n+1}=(n+1)^2-3(n+1)+12.

On \;a\;u_{n+1}-u_n=(n+1)^2-3(n+1)-(n^2-3n)

=n^2+2n+1-3n-3-n^2+3n

=2n-2.

2n-2\geqslant0\Leftrightarrow n\geqslant1.

d.\;u_n=\dfrac{1}{n}-\dfrac{1}{n+1}\;pour\;tout\; n\geqslant1.

u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}

Méthode 1 :

u_{n+1}-u_n=\dfrac{1}{n+1}-\dfrac{1}{n+2}-\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)

=\dfrac{2}{n+1}-\dfrac{1}{n+2}-\dfrac{1}{n}

=\dfrac{2n(n+2)}{n(n+1)(n+2)}-\dfrac{n(n+1)}{n(n+1)(n+2)}-\dfrac{(n+1)(n+2)}{n(n+1)(n+2)}

=\dfrac{2n(n+2)-n(n+1)-(n+1)(n+2)}{n(n+1)(n+2)}

=\dfrac{2n^2+4n-n^2-n-(n^2+3n+2)}{n(n+1)(n+2)}

u_{n+1}-u_n=\dfrac{-2}{n(n+1)(n+2)}

n(n+1)(n+2)>0 \text{ donc } \dfrac{-2}{n(n+1)(n+2)}<0.

u_{n+1}-u_n < 0.

On en déduit que la suite (un) est strictement décroissante.

\text{Pour tout entier naturel }n,

d.\;u_n=\dfrac{1}{n}-\dfrac{1}{n+1}\;pour\;tout\; n\geqslant1.

Pour\;tout\; n\geqslant1,\;\dfrac{1}{n}>\dfrac{1}{n+1}\;donc\;u_n>0.

u_n=\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1}{n(n+1)}.

u_{n+1}=\dfrac{1}{(n+1)(n+2)}.

\dfrac{u_{n+1}}{u_n}=\dfrac{\dfrac{1}{(n+1)(n+2)}}{\dfrac{1}{n(n+1)}}=\dfrac{n}{(n+2)}.

n+2>n\;donc\;\dfrac{n}{(n+2)}<1.

Pour\;tout\; n\geqslant1,\;\dfrac{u_{n+1}}{u_n}<1

donc la suite (un) est strictement décroissante.

Méthode 2 :

50 p 33

1. Reproduire la figure et représenter les cinq premiers termes de la suite sur l’axe des abscisses.

u_0

u_1

u_2

u_3

u_4

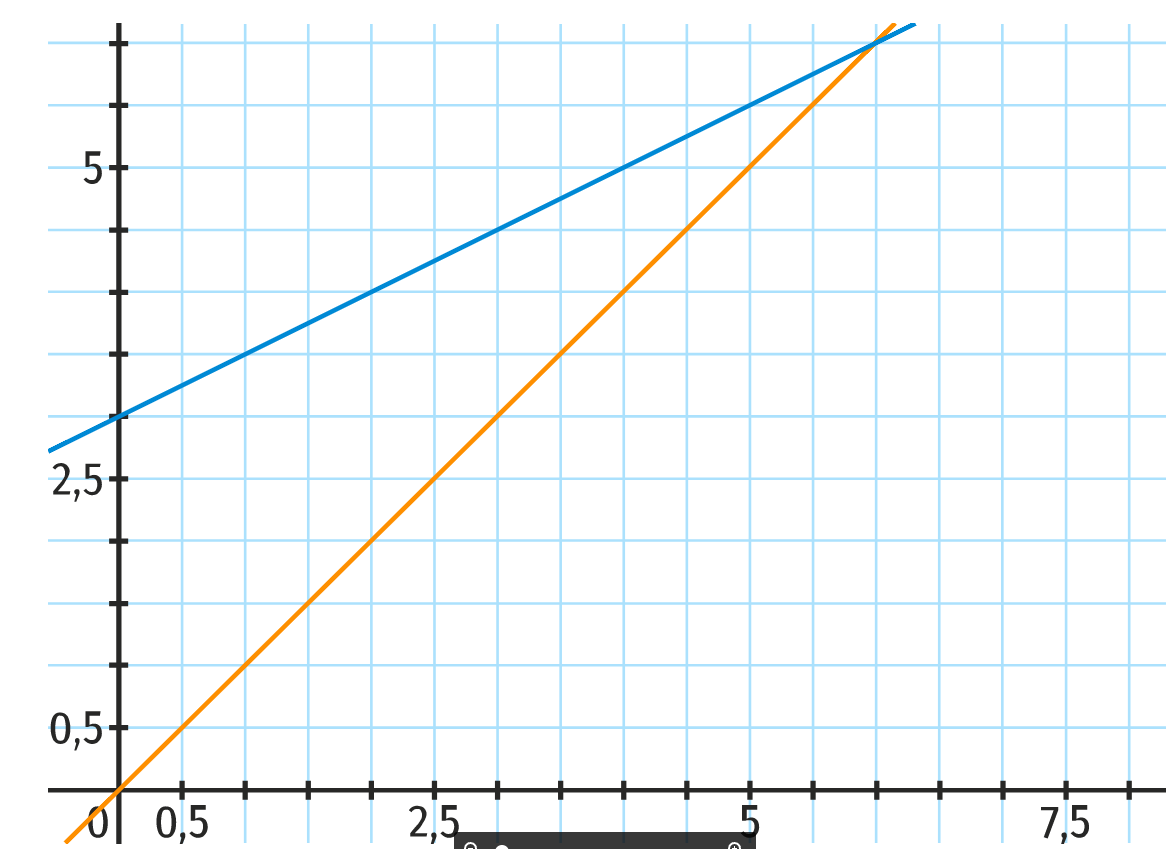
2. Conjecturer le sens de variation de la suite ($u_n$).

3. Conjecturer la limite de la suite.

La suite ($u_n$) semble croissante.

La limite de la suite ($u_n$) semble être 6.

52 p 34 :

Soit (un) la suite définie pour tout entier naturel n par

Représentation graphique :

u_n=\frac{3n-2}{n+1}.

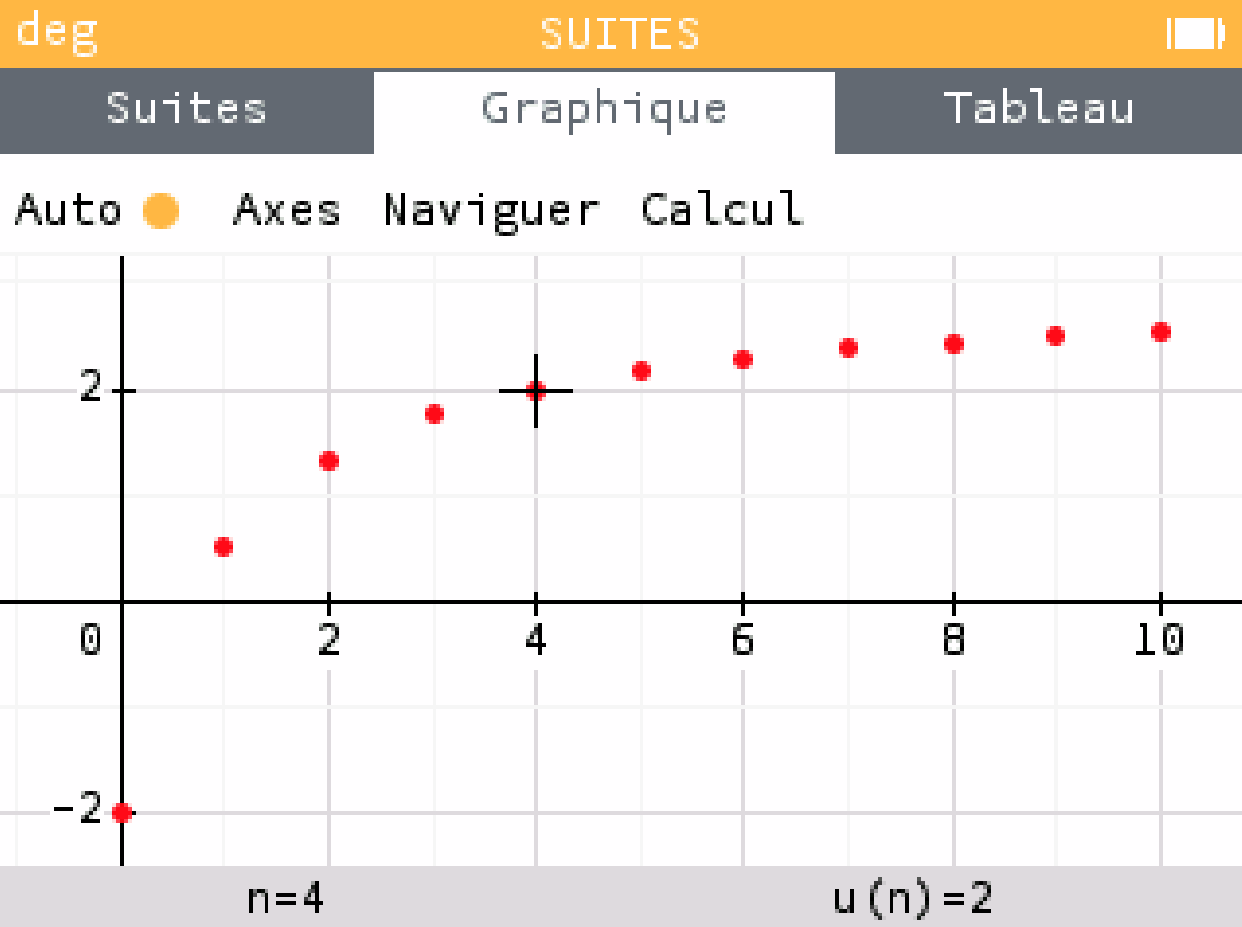
On conjecture que la suite est croissante et que sa limite est 3.

2. Prouver que la suite (un) est croissante.

On \;a\;u_{n}=\frac{3n-2}{n+1}\text{ et }u_{n+1}=\frac{3(n+1)-2}{(n+1)+1}=\frac{3n+3-2}{n+1+1}=\frac{3n+1}{n+2}.

u_{n+1}-u_n=\frac{(3n+1)(n+1)-(3n-2)(n+2)}{(n+2)(n+1)}

Par suite :

u_{n+1}-u_n=\frac{3n+1}{n+2}-\frac{3n-2}{n+1}

u_{n+1}-u_n=\frac{3n^2+3n+n+1-(3n^2+6n-2n-4)}{(n+2)(n+1)}

u_{n+1}-u_n=\frac{3n^2+3n+n+1-3n^2-6n+2n+4}{(n+2)(n+1)}

u_{n+1}-u_n=\frac{5}{(n+2)(n+1)}

Pour tout entier naturel n,

(n+2)(n+1)>0

On en déduit que la suite (un) est strictement croissante.

\text{donc }u_{n+1}-u_n>0.

3. Montrer que pour tout $n\geqslant 0,\;-2\leqslant u_n \leqslant 3$.

La suite ($u_n)$ est croissante et $u_0=-2$ donc pour tout entier $n$, $u_n\geqslant -2$.

u_{n}-3=\frac{3n-2}{n+1}-3

u_{n}-3=\frac{3n-2}{n+1}-\frac{3(n+1)}{n+1}

u_{n}-3=\frac{3n-2-3n-3}{n+1}

u_{n}-3=\frac{-5}{n+1}

Pour tout entier naturel $n$,

n+1>0

On en déduit que pour tout entier naturel $n$, $u_n<3$ .

\text{donc }u_n-3<0.

\dfrac{3n-2}{n+1}\geqslant 2,8

3n-2\geqslant 2,8 (n+1)

3n-2\geqslant 2,8 n+2,8

3n-2,8n\geqslant 2,8 +2

0,2n\geqslant 4,8

n\geqslant \dfrac{4,8}{0,2}

n\geqslant 24

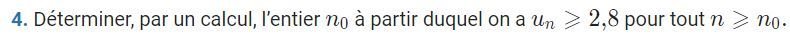
A partir de $n_0=24$ on a $u_n\geqslant 2,8$ pour tout $n\geqslant n_0$.

53 p 34 :

Soit (un) la suite définie pour tout entier naturel n par

u_n=5+\dfrac{3}{2n+1}.

Calculer les cinq premiers termes de la suite :

u_0=8\;;u_1=6\;;u_2=\dfrac{28}{5}\;;u_3=\dfrac{38}{7}\;;u_4=\dfrac{16}{3}.

2. Déterminer le sens de variation de (un).

On \;a\;u_{n+1}=5+\frac{3}{2n+3}.

u_{n+1}-u_n=\frac{3}{2n+3}-\frac{3}{2n+1}=\frac{3(2n+1)-3(2n+3)}{(2n+3)(2n+1)}

Par suite :

=\frac{-6}{(2n+3)(2n+1)}

Pour tout entier naturel n,

u_{n+1}-u_n<0

donc la suite (un) est strictement décroissante.

3. Calculer le plus petit entier

n_0\;tel\;que\;|u_n-5|\leqslant 0,001.

u_n-5 = \dfrac{3}{2n+1}>0\text{ donc }|u_n-5| = u_n-5 =\dfrac{3}{2n+1}

|u_n-5|\leqslant 0,001

\dfrac{2n+1}{3}\geqslant 1000

\dfrac{3}{2n+1}\leqslant \dfrac{1}{1000}

\text{donc }a\leqslant b\text{ si et seulement si }\dfrac{1}{a}\geqslant\dfrac{1}{b}

La fonction inverse est décroissante sur

]0\;;+\infty[\text{ et sur }]-\infty\;;0[

\text{On obtient }2n+1\geqslant 3000

\dfrac{2999}{2}=1499,5.

n\geqslant \dfrac{2999}{2} ;

\text{On a donc }n_0=1500.

On peut conjecturer que la limite de la suite (un) est 5.

\text{Quand }n\text{ devient grand, }\dfrac{3}{2n+1}\text{ se rapproche de }0.

4. Conjecturer la limite de la suite.

u_n =5+ \dfrac{3}{2n+1}

5. a) Algorithme ...

def limite(eps):
  n = 0
  u =  8
  while abs(u-5) > eps:
    n = n+1
    u =  5 + 3/(2*n+1)
  return n

print(limite(0.001), limite(1e-5), limite(1e-6))

# affiche 1500 150000 1500000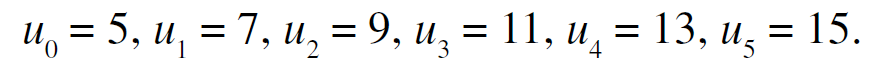

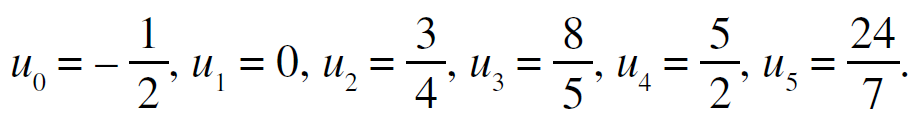
EX 1 : Dans chaque cas calculer les termes de u0 à u5 (Suites définie par une formule explicite) :

Exercices 2019

a) La suite (un) est définie pour tout entier naturel n par :

u_n=2n+5

b) La suite (un) est définie pour tout entier naturel n par :

u_n=\dfrac{n^2-1}{n+2}.

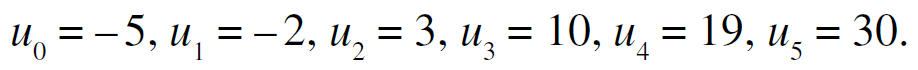
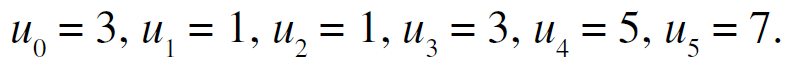
EX 2 : Dans chaque cas calculer les termes de u0 à u5 (Suites définie par une formule explicite) :

a) La suite (un) est définie pour tout entier naturel n par :

u_n=n^2+2n-5

b) La suite (un) est définie pour tout entier naturel n par :

u_n=|3-2n|

u_1=\dfrac{2\times u_0}{u_0+1}=\dfrac{10}{5+1}=\dfrac{5}{3}

u_2=\dfrac{2\times u_1}{u_1+1}=\dfrac{\frac{10}{3}}{\frac{5}{3}+1}=\dfrac{5}{4}

u_3=\dfrac{2\times u_2}{u_2+1}=\dfrac{\frac{10}{4}}{\frac{5}{4}+1}=\dfrac{10}{9}

u_4=\dfrac{2\times u_3}{u_3+1}=\dfrac{\frac{20}{9}}{\frac{10}{9}+1}=\dfrac{20}{19}

u_5=\dfrac{2\times u_4}{u_4+1}=\dfrac{\frac{40}{19}}{\frac{20}{19}+1}=\dfrac{40}{39}

\left\{\begin{array}{l} u_0 = 5 \\ u_{n+1} = \dfrac{2u_n}{u_n+1} \end{array}\right.

EX 3 : Dans chaque cas calculer les termes de u1 à u5 (Suites définie par une relation de récurrence) :

a) La suite (un) est définie pour tout entier naturel n par :

b)\;f(x)=(x+1)^2

u_1=(u_0+1)^2=(-1+1)^2=0

u_2=(u_1+1)^2=(0+1)^2=1

u_3=(u_2+1)^2=(1+1)^2=4

u_4=(u_3+1)^2=(4+1)^2=25

u_5=(u_4+1)^2=(25+1)^2=676

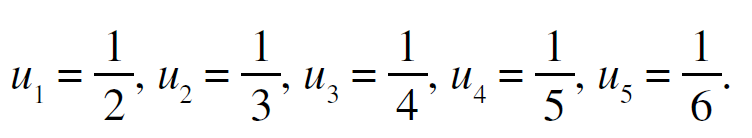
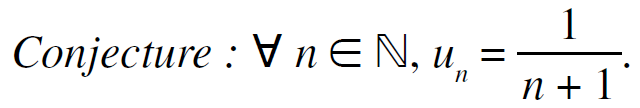
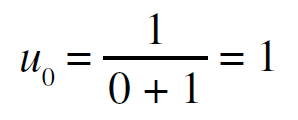
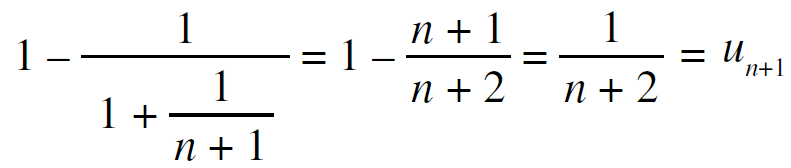
EX 4 :

1-\dfrac{1}{1+u_n}=

\left\{\begin{array}{l} u_0 = 1 \\ u_1 = 2 \\ u_{n+2} = 2u_{n+1}+u_n \end{array}\right.

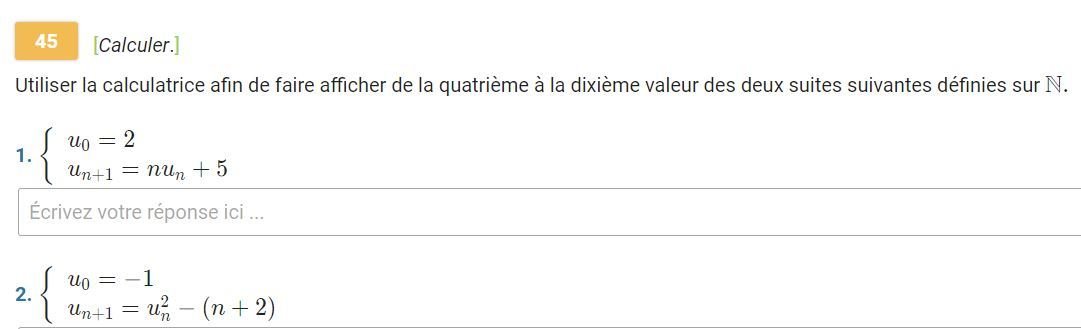
EX 5 : Calculer les termes de (u2) à (u4) dans les deux cas suivants :

a) La suite (un) est définie pour tout entier naturel n par :

Pour\;n=0,\;on\;a\;u_2=2u_1+u_0=2\times 2+1 =5

Pour\;n=1,\;on\;a\;u_3=2u_2+u_1=2\times 5+2 =12

Pour\;n=2,\;on\;a\;u_4=2u_3+u_2=2\times 12+5 =29

\left\{\begin{array}{l} u_0 = 1 \\ u_1 = 2 \\ u_{n+2} = u_{n+1}+n \end{array}\right.

b) La suite (un) est définie pour tout entier naturel n par :

Pour\;n=0,\;on\;a\;u_2=u_1+0= 2+0=2

Pour\;n=1,\;on\;a\;u_3=u_2+1=2+1 =3

Pour\;n=2,\;on\;a\;u_4=u_3+2=3+2 =5

EX 6 : On considère L'algorithme suivant :

u \leftarrow 1 \\ pour \;i\leftarrow1\;à\;10\;faire \\ u\leftarrow\dfrac{u-1}{u-2}\\ fin

Que calcule cet algorithme ?

u_{n+1}\;et\; u_n.

Écrire une relation entre

Les termes de u1 à u10 d'une suite définie par récurrence dont le premier terme est u0 = 1.

u_{n+1}=\dfrac{u_n-1}{ u_n-2}.

EX 8 : Représentation graphique d'une suite définie par récurrence

u_0 = 1

u_{n+1} = \dfrac{1}{2}u_n+1

u_{n+1} =f(u_n)\;avec\;f(x) =\dfrac{1}{2}x+1

f est une fonction affine, sa représentation graphique est la droite d'équation :

y=\dfrac{1}{2}x+1

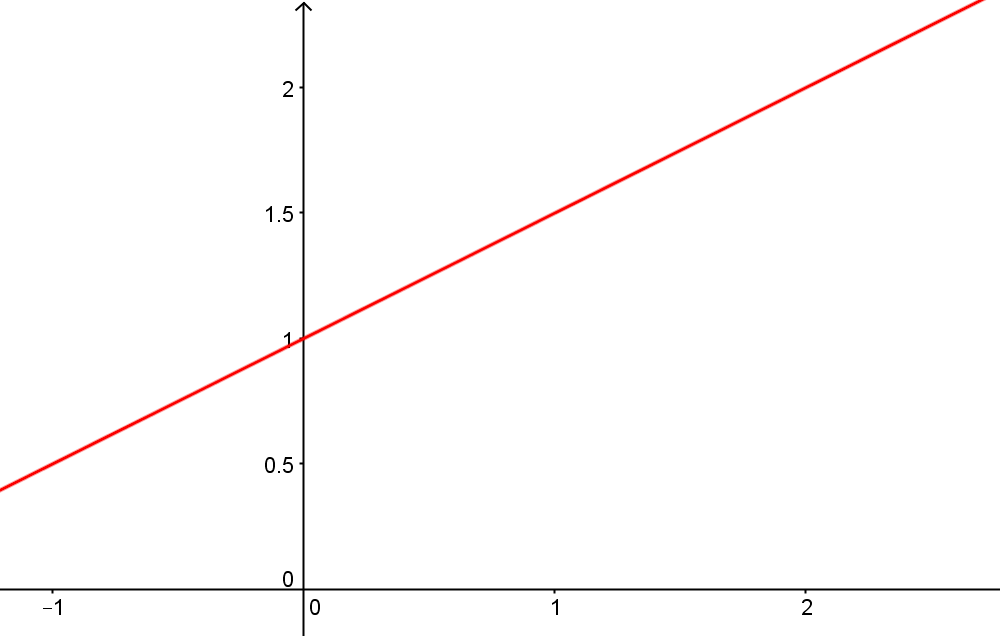
On construit ensuite la droite d'équation y = x

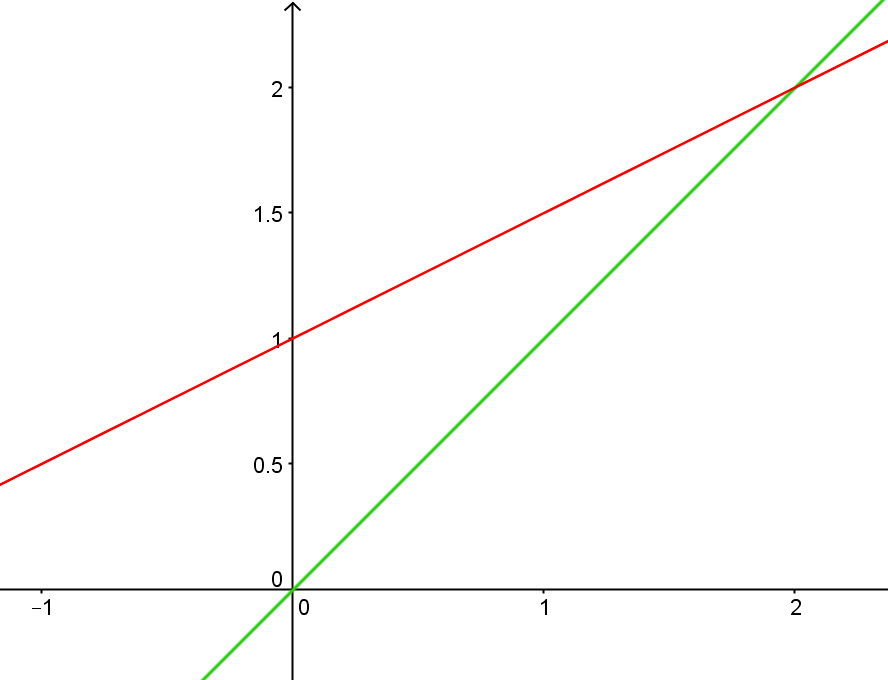
On repère u0 sur l'axe des abscisses

u_0

u_1 = f(u_0)

u_1

On reporte ensuite u1 sur l'axe des abscisses

On recommence...

u_0

u_1

u_2= f(u_1)

u_2

u_3= f(u_2)

u_3

u_4

On conjecture que la suite est croissante et converge vers 2.

\text{4. Déterminer l'entier }n_0\text{ à partir duquel on a }u_n\geqslant 2,8 \text{ pour tout } n\geqslant n_0.

\frac{3n-2}{n+1}\geqslant 2,8

3n-2\geqslant 2,8(n+1)

n+1>0\text{ donc}

3n-2\geqslant 2,8n+2,8

0,2n\geqslant 4,8

n\geqslant \dfrac{4,8}{0.2}

n\geqslant 24

\text{A partir de }n_0=24\text{, on a pour tout } n\geqslant n_0,\;u_n\geqslant 2,8.

Quantificateurs logiques

pour tout (ou quelque soit)

\forall

il existe

\exists

il n'existe pas

\nexists