Arithmétique

p 29

p 29

p 29

Compléments sur le PGCD et le PPCM

PGCD de 275 et 75 avec l'algorithme d'Euclide

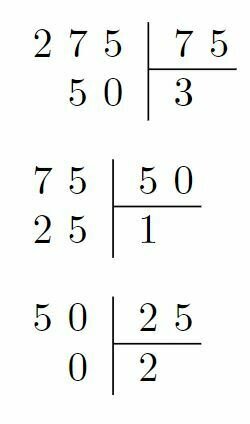
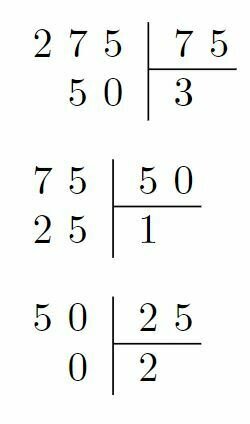
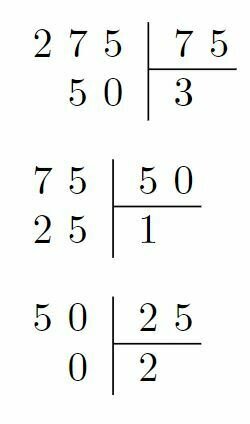
On commence par diviser 275 par 75.

On continue en prenant le diviseur et le reste de la division précédente soit 75 et 50 .

On continue en prenant le diviseur et le reste de la division précédente soit 50 et 25.

On s'arrête lorsque le reste est égal à 0.

On cherche le Plus Grand Diviseur Commun à 275 et 75.

Le PGCD est le dernier reste non nul.

Ici le PGCD de 275 et 75 est donc 25.

PGCD de 275 et 75 avec avec décomposition en facteurs premiers

275=5\times 55 =5\times 5 \times 11 = 5^2 \times 11
75=3\times 25 =3\times 5^2

On cherche le Plus Grand Commun Diviseur  à 275 et 75.

Le PGCD de 275 et 75 est :

5^2=25

PGCD de 35000 et 1200 avec avec décomposition en facteurs premiers

35000=35\times 1000 =7\times 5 \times (10)^3 = 7 \times 5 \times 2^3\times 5^3= 2^3\times 5^4\times 7
1200=3\times 4 \times 100 = 3\times 2^2 \times 10^2=3\times 2 ^2\times 2^2\times 5^2=2^4\times 3 \times 5^2

Le PGCD de 35000 et 1200 est :

2^3\times 5^2=200
35000= 2^3\times 5^2\times 5^2 \times 7
1200= 2^3\times 5^2\times 2 \times 3

PPCM de 275 et 75 avec avec décomposition en facteurs premiers

275=5\times 55 =5\times 5 \times 11 = 5^2 \times 11
75=3\times 25 =3\times 5^2

On cherche le Plus Petit Multiple Commun à 275 et 75.

Le PPCM de 275 et 75 est :

3\times 5^2 \times 11=825

(en nombres de dalles)

x \text{ et }x+5 \text{ sont des diviseurs positifs de 36}
1 \times 36 = 36 \text{ ; si }x=1 \text{ alors }x+5=36 \Leftrightarrow x= 31 \text{ : impossible }
2 \times 18 = 36 \text{ ; si }x=2 \text{ alors }x+5=18 \Leftrightarrow x= 13 \text{ : impossible }
3 \times 12 = 36 \text{ ; si }x=3 \text{ alors }x+5=12 \Leftrightarrow x= 7 \text{ : impossible }
4 \times 9 = 36 \text{ ; si }x=4 \text{ alors }x+5=9 \Leftrightarrow x= 4 \text{ : 4 est solution }
6\times 6 = 36 \text{ ; si }x=6 \text{ alors }x+5=6 \Leftrightarrow x=1 \text{ : impossible }
\text{Cette équation admet une unique solution entière, }x= 4.

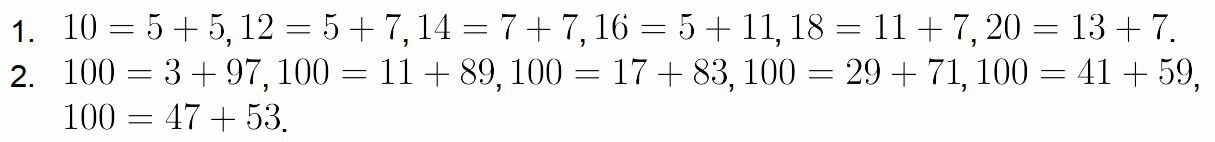
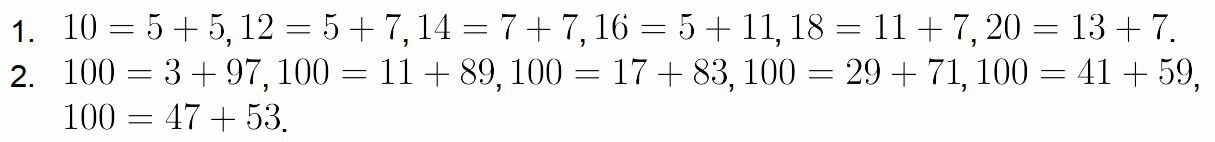
On procède comme dans l'exercice précédent.

\text{Cette équation admet une unique solution entière, }x= 3.
\text{Cette équation admet une unique solution entière, }x= 6.

Raisonnement par disjonction des cas :

Lorsque la démonstration d'une propriété dépend de la valeur de n, on sépare le raisonnement suivant toutes les valeurs que peut prendre n. On peut, comme ci-dessus, séparer les cas où n est un entier pair des cas où n est impair, ou encore séparer les cas où n est un réel positif des cas où il est strictement négatif.

Made with Slides.com