Échantillonnage & Simulation
1 Simulation d’expérience
1.1 Un exemple pour comprendre
On lance un dé équilibré à 6 faces, numérotées de 1 à 6, et on note le numéro obtenu.
Il s'agit d'une expérience aléatoire, on connait toutes les issues possibles {1, 2, 3, 4, 5, 6} mais on ne peut prévoir avec certitude laquelle va se réaliser.
On s'intéresse à l'événement : "Obtenir un 6"
Sa probabilité est de 1/6.
Si on lance 6 fois un dé, est-on sûr d'obtenir un 6 ?
Si on lance 50 fois le même dé, combien de fois va-t-on obtenir le 6 ?
Si on lance 5000 fois le même dé, combien de fois va-t-on obtenir le 6 ?
On s'intéresse à la fréquence d'apparition du 6 lorsque l'on réalise un grand nombre de lancers, c'est à dire lorsque l'on répète un grand nombre de fois la même expérience aléatoire.
1.2 Notion d'échantillon
On reprend l'exemple précédent. On considère le lancer du dé comme une expérience aléatoire à deux issues :
- "obtenir un 6", appelée succès.
- "ne pas obtenir un 6", appelée échec.
Lorsque l'on répète 50 fois cette expérience, la donnée des résultats, s'appelle un échantillon de taille 50.
Pour des raisons pratiques, il est nécessaire de simuler l'expérience.
On peut notamment utiliser un tableur ou une calculatrice.
La répétition de 5000 lancers nous donne un échantillon de taille 5000...
1.3 Fluctuation d'échantillonnage
Un tableur possède un générateur de nombres aléatoires.
La fonction ALEA( ) permet d’obtenir un nombre au hasard compris entre 0 et 1 et distinct de 1.
La fonction ENT est la fonction partie entière.
La fonction 6*ALEA( ) permet donc d’obtenir un nombre au hasard compris entre 0 et 6 et distinct de 6.
La fonction 6*ALEA( ) + 1 permet d’obtenir un nombre au hasard compris entre 1 et 7 et distinct de 7.
La fonction ENT(6*ALEA( ) + 1) permet au final d’obtenir un nombre entier au hasard entre 1 et 6.
Afin d'observer ce phénomène, nous allons créer des échantillons à l'aide d'un tableur.
Entrer la formule =ENT(6*ALEA( ) + 1) dans la cellule A1 d'une feuille de calcul :
Simulation de 6 lancers sur un tableur :
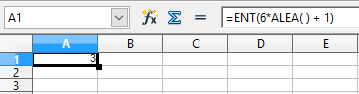
ici le tableur renvoie de façon aléatoire un 3.
Tirer sur la poignée jusqu'à la ligne 6 :

Nous avons créé un échantillon de taille 6.
Ici, la fréquence observée d'apparition du 6 est égale à 0 (0/6=0). Et pour votre échantillon ?
La fréquence observée fluctue d'un échantillon à l'autre, on parle de fluctuation d’échantillonnage.
La fréquence observée fluctue autour de la probabilité théorique d'obtenir un 6, 1/6 soit environ 0,17.
Quelle est la fréquence maximale observée ?
Simulation de 50 lancers sur un tableur :
Tirer sur la poignée jusqu'à la ligne 50.
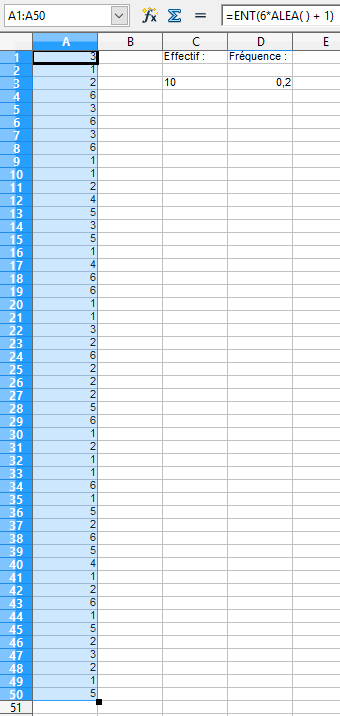
Nous avons créé un échantillon de taille 50.
Sur cet échantillon de taille 50, pour compter le nombre de fois où le 6 est apparu (l'effectif du 6) on utilise la fonction NB.SI(plage;critère)
Ici entrer =NB.SI(A1:A50;6) dans la cellule C3.
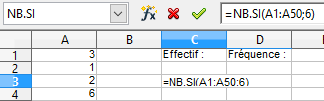
Pour calculer la fréquence observée d'apparition du 6 :
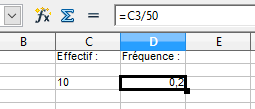
Entrer =C3/50 dans la cellule D3.
Il est aisé de créer un autre échantillon de même taille en simulant 50 nouveaux lancers... Pour cela presser la touche F9.
Ici, la fréquence observée d'apparition du 6 est égale à 0,2 (10/50=0,2). Et pour votre échantillon ?
On constate une nouvelle fois que la fréquence observée fluctue autour de 1/6.
Quelle est la fréquence minimale observée ?
Quelle est la fréquence maximale observée ?
Simulation de 5000 lancers sur un tableur :
Entrer la formule =ENT(6*ALEA( ) + 1) dans la cellule A1 d'une nouvelle feuille de calcul.
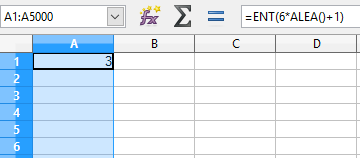
Entrer A1:A5000 dans la zone de saisie des plages de cellules :
Puis cliquer sur Ctrl+D
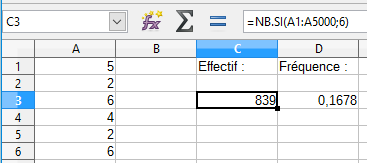
On procède de la même façon pour déterminer l'effectif et la fréquence du 6 dans l'échantillon de taille 5000 ainsi créé :
Entrer =NB.SI(A1:A5000;6) dans la cellule C3 puis =C3/5000 dans la cellule D3 :
Ici, la fréquence observée d'apparition du 6 est égale à 0,1678 (839/5000=0,1678). Et pour votre échantillon ?
On constate une nouvelle fois que la fréquence observée fluctue autour de 1/6.
Quelle est la fréquence minimale observée ?
Quelle est la fréquence maximale observée ?
Nous avons observé lors de nos simulations que plus la taille de l'échantillon augmente moins la fréquence observée fluctue. Les valeurs se stabilisent autour de la probabilité théorique de 1/6.
Plus généralement, on a la propriété suivante :
Propriété : (admise)
Soit un caractère dont la proportion dans une population donnée est p.
alors dans 95 % des échantillons de taille \(n\) la fréquence observée du caractère appartiendra à l’intervalle :
Cet intervalle est appelé intervalle de fluctuation au seuil de 95 %.
2 Intervalle de fluctuation au seuil de 95%
Exemple : On reprend nos deux échantillons précédents, respectivement de taille 50 et de taille 5000 :
2.1 Intervalle de fluctuation
Remarque :
Plus la taille de l'échantillon augmente plus la longueur de l'intervalle diminue ce qui correspond à la baisse de la fluctuation d'échantillonnage observée lors de nos simulations.
- Pour un échantillon de taille 50, un intervalle de fluctuation de la fréquence au seuil de 95% est l'intervalle :
Cela signifie que pour 95% des échantillons de taille 50 la fréquence d'apparition du 6 appartient à l'intervalle I.
- Pour un échantillon de taille 5000, un intervalle de fluctuation de la fréquence au seuil de 95% est l'intervalle :













2.2 Intervalle de confiance
Définition - Propriété :
on peut estimer que la proportion p du caractère dans la population totale vérifie :
avec une probabilité d'au moins 0,95.
Cet intervalle est appelé intervalle de confiance au seuil de 95%.
Soit un caractère dont la proportion p dans une population est inconnue. On cherche à estimer p en étudiant un échantillon de taille n dans lequel la fréquence observée du caractère est f.
Exemple :

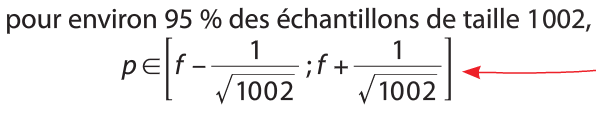
intervalle de confiance au seuil de 95%




