Équations de droites
Automatismes
Introduction
Exercices
Automatismes
Série 1 : 15 questions




























5) Quel est le coefficient directeur de la droite (HE) ?


6) Quel est le coefficient directeur de la droite (AF) ?


7) Quelle est l'ordonnée à l'origine de la droite (HE) ?


8) Quelle est l'ordonnée à l'origine de la droite (AF) ?


9) Donner l'équation réduite de la droite (AF)


10) Donner l'équation réduite de la droite (HE)
Automatismes
Série 2 : 13 questions
Quelle est l'ordonnée du point de \(d\) d'abscisse 4 ?
Quelle est l'abscisse du point de \(d\) d'ordonnée 11 ?
Quelle est son coefficient directeur ?
Quelle est son ordonnée à l'origine ?
Le point de coordonnées \( (7~;~5) \) appartient-il à \(d\) ?
Quelle est son équation réduite ?
\(d\) et \(d'\) sont-elles sécantes ou parallèles ?
Quelles sont les coordonnées du point d'intersection de \(d\) et \(d'\) ?
\(d\) et \(d'\) sont-elles sécantes ou parallèles ?
Déterminer une équation réduite de la droite (AB).
Équations de droites
Introduction :
On considère les points \(A(1~;-5)\) et \(B(-3~;2)\) du plan muni d'un repère.
Que peut-on dire des points \(M(x~;~y)\) tels que \(\overrightarrow{AM}\) et \(\overrightarrow{AB}\) sont colinéaires ?
Ils appartiennent à la droite (AB).
Existe-t-il une relation qui caractérise les coordonnées \(x\) et \(y\) d'un point M de la droite (AB) ?
\(A(1~;-5)\) ; \(B(-3~;2)\) ; \(M(x~;y)\)
Cette relation s'appelle équation cartésienne de la droite (AB).
Cette relation est vérifiée par les couples de coordonnées des points de la droite (AB) et par eux seuls.
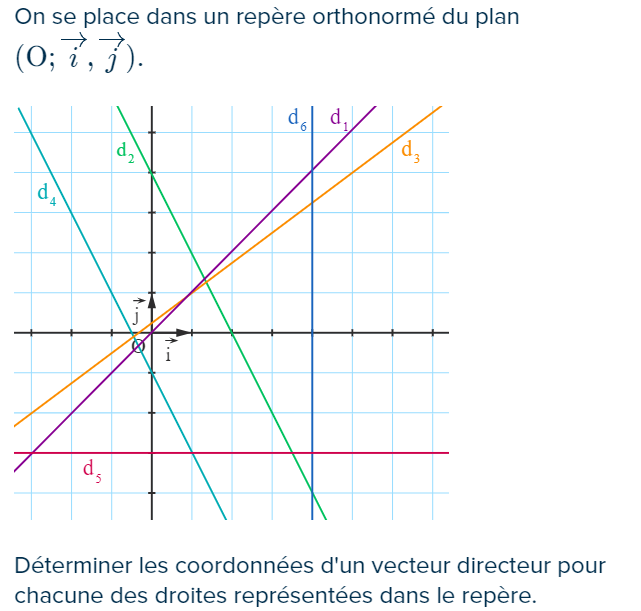
37 p 230

38 p 230

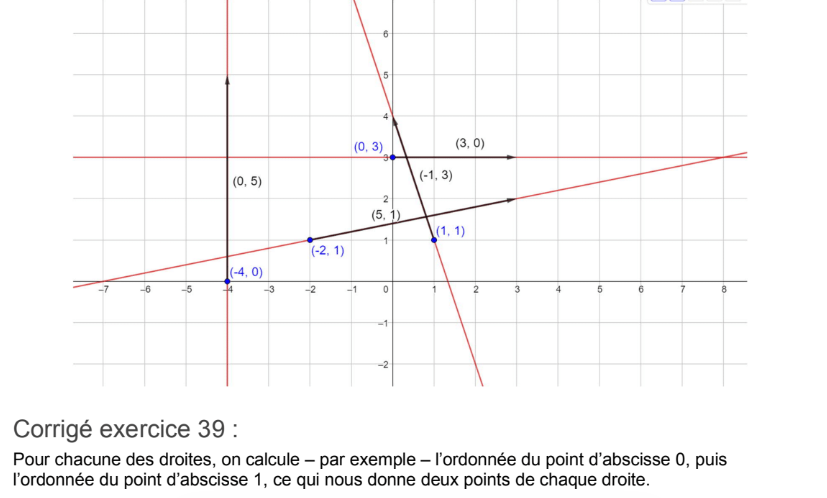
39 p 230


Rq. On peut aussi calculer l'abscisse du point de \(d_1\) d'ordonnée 0, on a le choix.
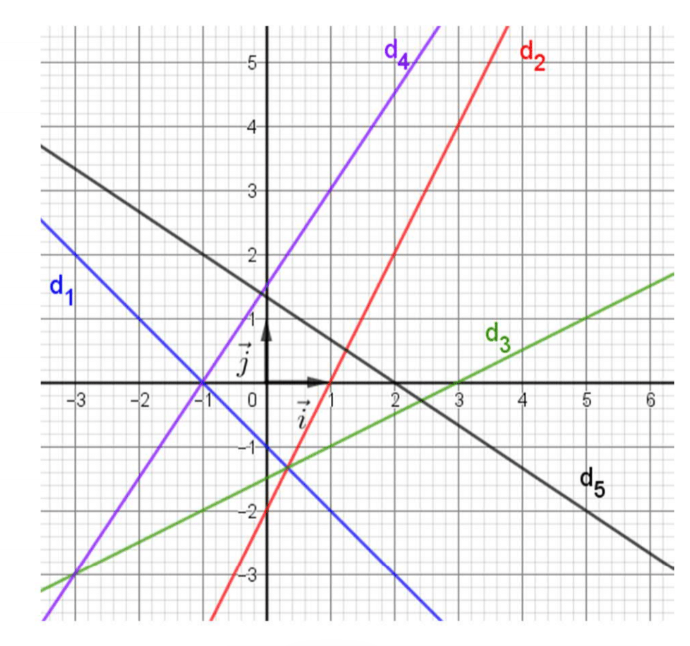
44 p 230

On regarde si les coordonnées du point A vérifient ou pas l'équation de la droite d :






45 p 230









48 p 230







57 p 233

Coefficient directeur d'une droite

Coefficient directeur de la droite (AB)

La droite "monte"
Un autre exemple :
La droite "descend"
Un autre exemple :

D'autres exemples :



D'autres exemples :



57 p 233



Méthode 1 :
Méthode 2 :
59 p 233

Méthode : placer le point A puis "compter les carreaux "
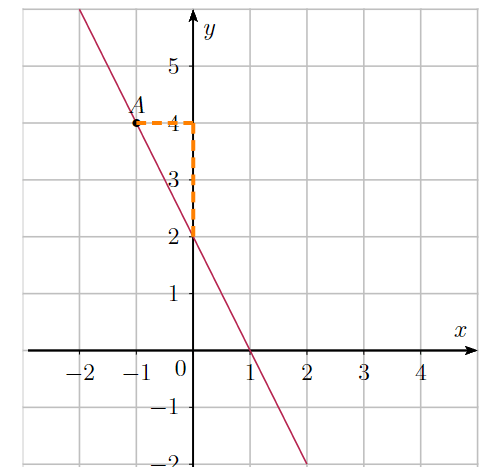
59 p 233

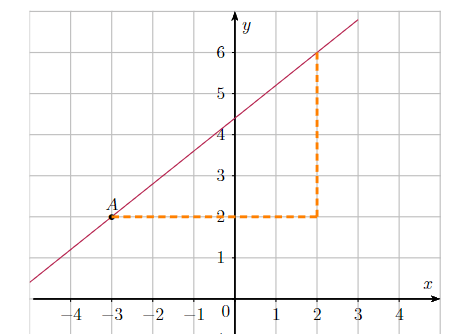

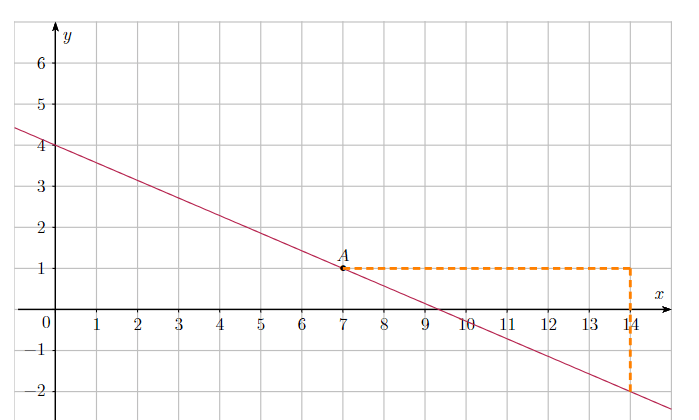
60 p 233
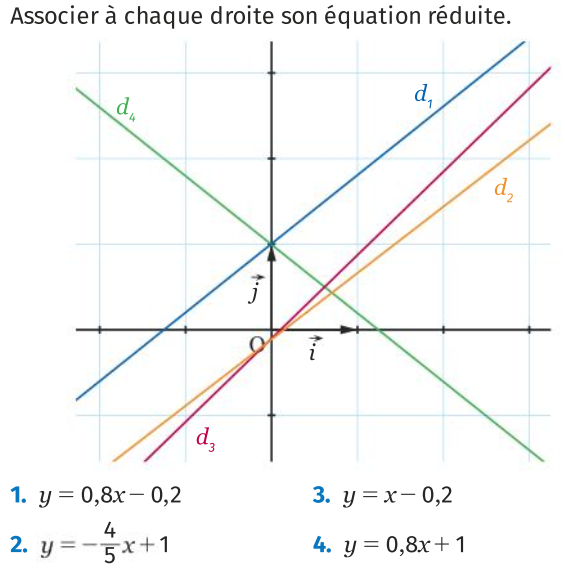

61 p 233

Méthode 1 : Comme pour les équations cartésiennes, on détermine deux points de chaque droite en choisissant des valeurs pour remplacer \(x\) ou \(y\) :
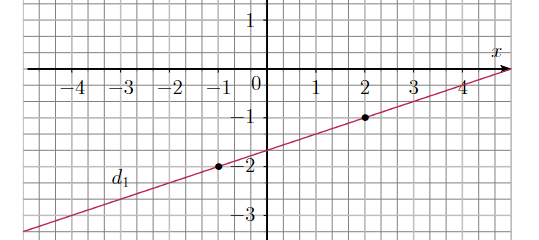
61 p 233

Méthode 2 : On procède comme dans l'exercice 59 p 233 :
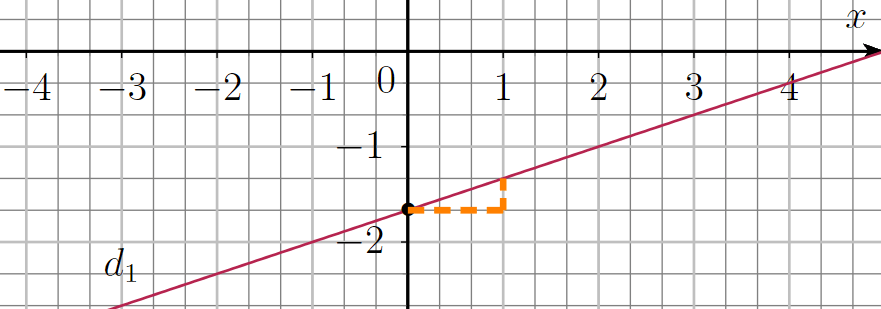

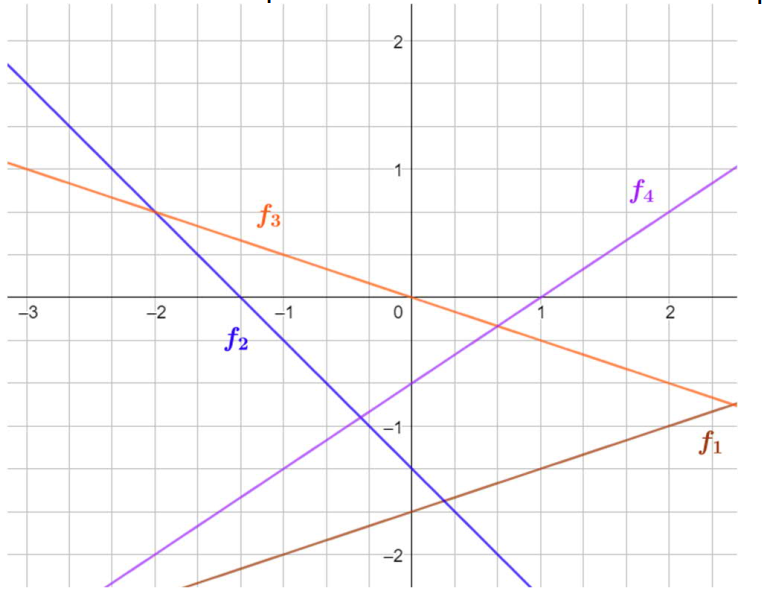



donc la droite \((AB)\) a une équation de la forme
b) On calcule m le coefficient directeur de la droite :
1. Méthode :
a) On commence par comparer les abscisses des 2 points :

2. \(x_A=x_B=5\) donc \((AB)\) a pour équation réduite \(x=5\).

3. \(x_A\ne x_B\) donc la droite \((AB)\) a une équation de la forme \(y=mx+p\).
78 p 235

Résolution du système avec la méthode par substitution :
Dans la première équation on exprime \(y\) en fonction de \(x\) :
Dans la deuxième équation on substitue à \(y\) l'expression obtenue :
On résout l'équation :
On détermine la deuxième inconnue :
Conclusion :
Le couple \((1~;~4)\) est la solution du sytème\(\left\{\begin{array}{rcl} x-y+3&=&0 \\ 3x+4y-19&=&0\end{array}\right.\).
Les droites d'équations respectives \(x-y+3=0\) et \(3x+4y-19=0\) sont donc sécantes et leur point d'intersection a pour coordonnées \((1~;~4)\).
Résolution du système avec la méthode par combinaisons :
On soustrait membre à membre les deux équations :
On obtient une équation à une inconnue que l'on peut résoudre :
On ajoute membre à membre les deux équations :
On obtient une équation à une inconnue que l'on peut résoudre :
82 p 236
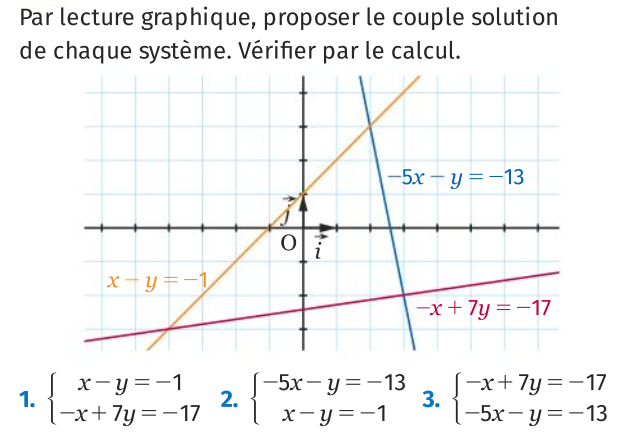

Précédente version
65 p 233

Les droites \(d\) et \(d'\) sont parallèles donc un vecteur directeur de \(d\) est aussi un vecteur directeur de \(d'\).
On en déduit que \(d'\) a une équation de la forme \(2x+y+c=0\).
C'est la cas du vecteur \(\overrightarrow{u}\begin{pmatrix} -1\\ 2 \end{pmatrix}\).
\(A\in d'\) donc \(2\times (-1)+5+c=0\).
On obtient \(c=-3\).
En conclusion, une équation cartésienne de \(d'\) est donc \(2x+y-3=0\).





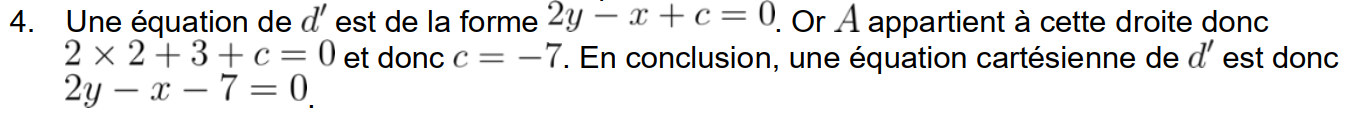
69 p 233


1 Rappels sur les fonctions affines
Définition : Soient m et p deux réels.
La fonction f définie sur par est une fonction affine.
Le coefficient m est appelé coefficient directeur.
Le coefficient p est appelé ordonnée à l’origine.

Propriété : La représentation graphique de la fonction affine f définie sur par est une droite.
Cette droite passe par le point de coordonnées (0 ; p).

Équations de droites
2 Équations de droites
Propriété : Dans un repère (O ; I ; J), toute droite D non parallèle à l’axe des ordonnées est la représentation graphique d’une fonction affine.
Elle admet donc une équation de la forme y = mx + p.
Le coefficient m est appelé coefficient directeur.
Le coefficient p est appelé ordonnée à l’origine.
Démonstration :
La droite D n’étant pas parallèle à l’axe des ordonnées, elle le coupe en un point A.

D
Elle coupe aussi la parallèle à l’axe des ordonnées passant par le point I.
On note B le point d’intersection.
On a donc A (0 ; p) et B (1 ; q).
Soit f la fonction affine définie par
La représentation graphique de la fonction affine f est donc une droite qui passe par A(0 ; p) et B(1 ; q).
Comme la seule droite passant par les points A et B est la droite D, la droite D est la représentation graphique de la fonction affine f et admet comme équation y = mx + p (en posant m = q – p).
On a :
et
Remarque :
L'équation d'une droite est l'équation vérifiée par les coordonnées (x ; y) de chacun de ses points et eux seuls.
Propriété : Dans un repère (O ; I ; J), toute droite parallèle à l’axe des ordonnées admet une équation de la forme .
Démonstration :
La droite étant parallèle à l’axe des ordonnées, elle coupe l’axe des abscisses en un point A.

Un point M (x ; y) est sur si et seulement si il a la même abscisse que A.
La droite admet donc comme équation .
3 Coefficient directeur d’une droite
Propriété :
Dans un repère, on considère les points
Le coefficient directeur de la droite (AB) est :
avec
Démonstration :
Comme , la droite (AB) n’est pas parallèle à l’axe des ordonnées. Elle admet donc une équation de la forme
Comme les points A et B sont sur cette droite, on a :
Comme , on peut diviser cette expression par

On obtient
Méthodes : Déterminer l'équation d'une droite
a) graphiquement
Il s'agit de lire sur un graphique m, le coefficient directeur de la droite ainsi que p, son ordonnée à l'origine.
Pour la lecture de m, le coefficient directeur de la droite on repère 2 nœuds de quadrillage appartenant à la droite :

La droite "monte"

La droite "descend"





Cas particulier :

Pour la lecture de p, on lit l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées :





b) par le calcul
Méthode : Déterminer une équation de droite
b) par le calcul

1. Méthode 1 :
donc la droite (AB) a une équation de la forme
On continue en calculant m :
On commence par regarder les abscisses des 2 points :
On remplace m par sa valeur dans l'équation :
Pour calculer p, on remplace dans l'équation x et y par les coordonnées de A ou de B :
3 = -2 x 1 + p ou 7 = -2 x (-1) + p
ce qui nous donne p = 5.
Conclusion : (AB) a pour équation :
1. Méthode 2 :
Soit M(x ; y) un point de la droite (AB) :
Les vecteurs et sont colinéaires donc
Équation cartésienne
Équation réduite
2.
Le point C (2 ; y) appartient à la droite (AB) donc ses coordonnées vérifient l'équation de (AB) : y = -2 x 2 + 5.
3.
De même le point D (x ; -2) appartient à la droite (AB) donc ses coordonnées vérifient également l'équation de (AB) :
On obtient y = 1. L'ordonnée de C est 1.
On résout l'équation et on obtient
L'abscisse de D est


1
2



4 Positions relatives de deux droites
Théorème 1 (admis) : Dans un repère, on considère la droite D d’équation y = mx + p et la droite D' d’équation y = m'x + p.
Dire que D et D' sont parallèles équivaut à m = m'.
Théorème 2 : Dans un repère, on considère la droite D d’équation y = mx + p et la droite D' d’équation y = m'x + p.
Dire que D et D' sont sécantes équivaut à
Théorème 3 : Dans un repère, on considère trois points A, B et C tels que l’abscisse de A soit différente de celle de B et de celle de C.
Les points A, B et C sont alignés si et seulement si les coefficients directeurs de (AB) et (AC) sont égaux.
Démonstration :
Comme l’abscisse de A est différente de celle de B et de C, les droites (AB) et (AC) ne sont pas parallèles à l’axe des ordonnées.
Donc, d’après le Théorème 1, dire que (AB) // (AC) équivaut à dire que les coefficients directeurs de (AB) et (AC) sont égaux.
De plus, comme les droites (AB) et (AC) ont un point commun (le point A), dire qu’elles sont parallèles revient à dire qu’elles sont confondues et donc que les points A, B et C sont alignés.

d1 a pour coef. directeur :
d2 a pour coef. directeur :
donc les droites d1 et d2 ne sont pas parallèles.


est parallèle à d donc a le même coefficient directeur que d. il s'agit simplement de trouver p, son ordonnée à l'origine.










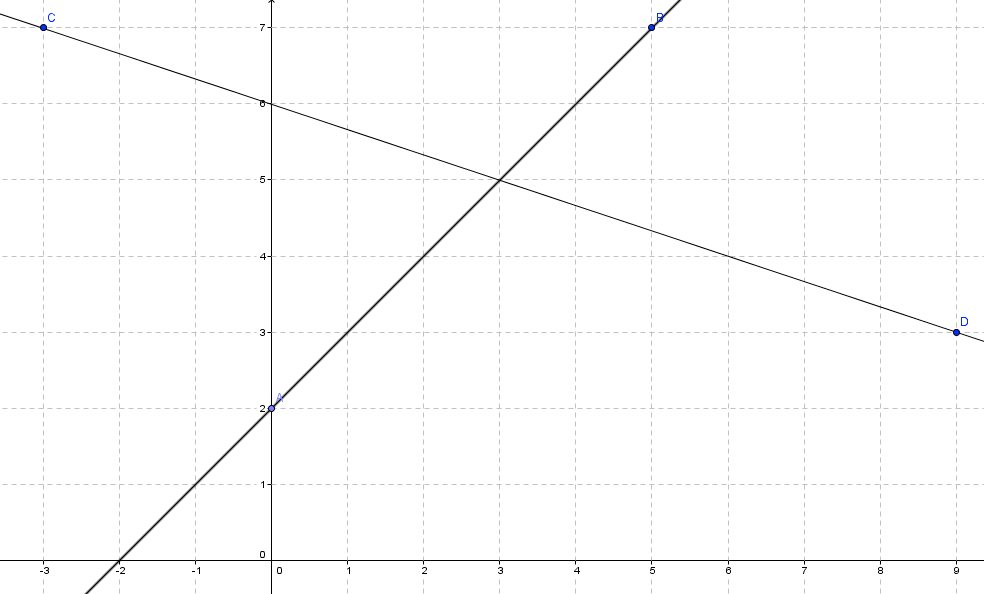

Pour démontrer que deux droites sont sécantes, on montre que leurs coefficients directeurs sont différents :

1
1
3
-1


p'= 6
p= 2


M
Soit M(x ; y) le point d'intersection des droites (AB) et (CD).







