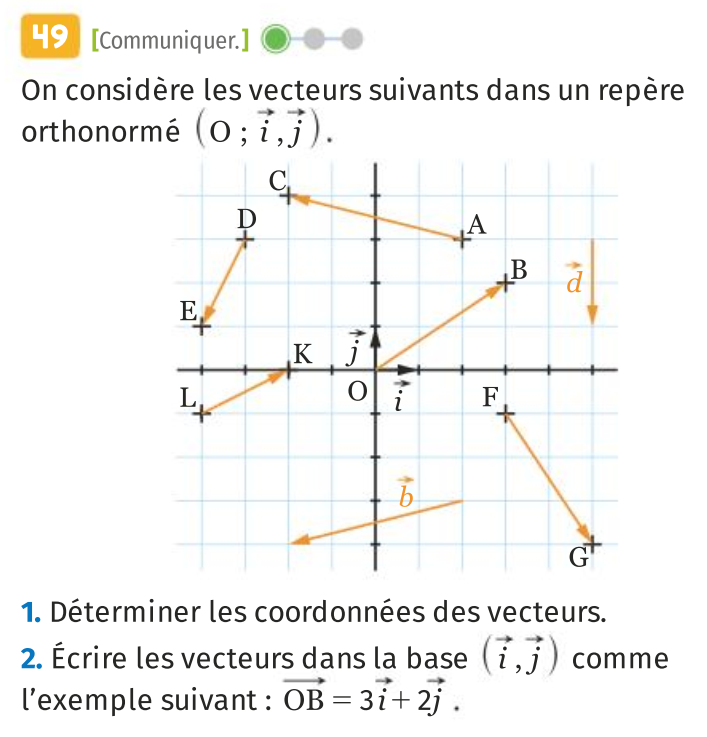
Configurations du plan
Act. A p 172



H


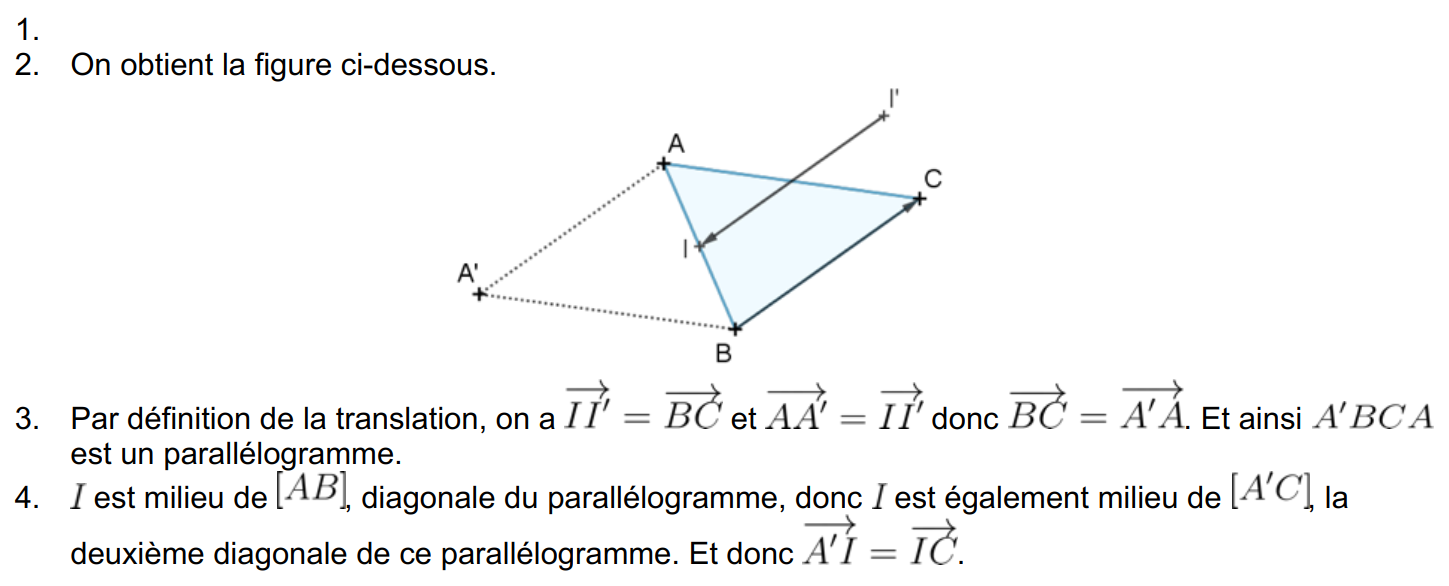
V






H
V
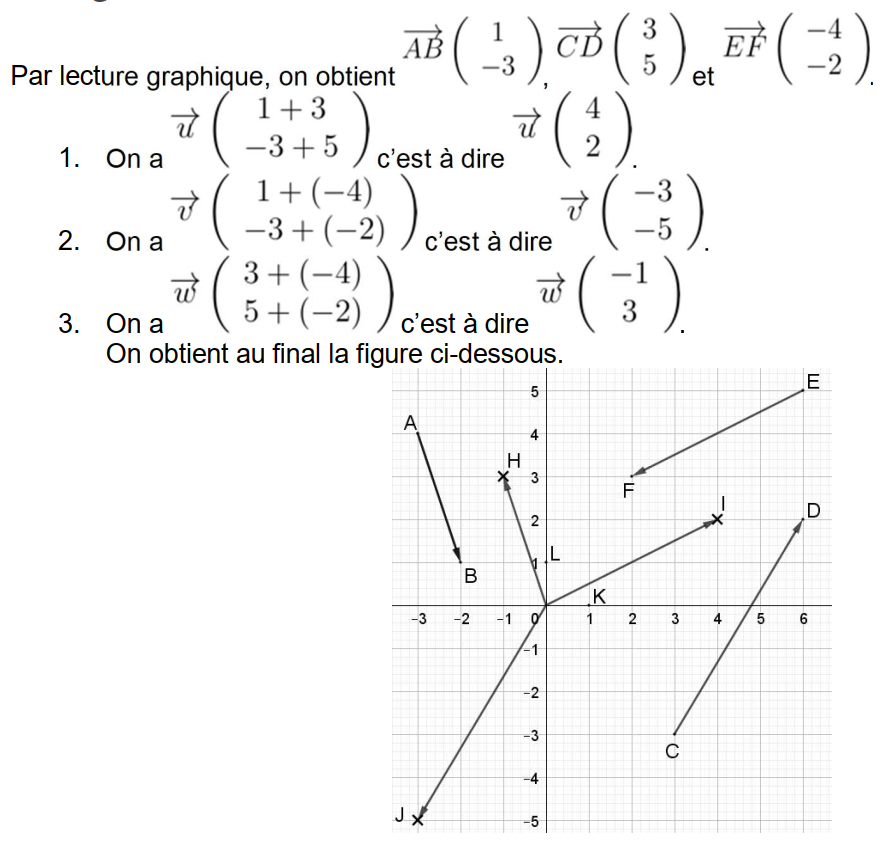
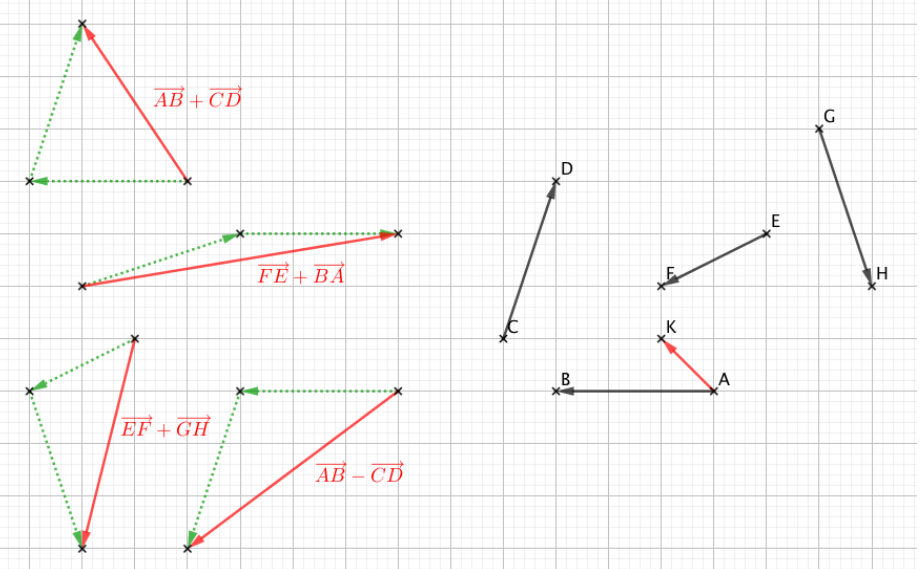
On peut écrire par exemple :
- Si \(EDAH\) est un parallélogramme alors les vecteurs \(\overrightarrow{ED}\) et \(\overrightarrow{HA}\) sont égaux.
- Si le point F est l’image du point V par la translation de vecteur \(\overrightarrow{DA}\) alors VDAF est un parallélogramme.


I
J

On peut passer du point H au point J par la translation de vecteur \(\overrightarrow{DM}\).
- Les trois caractéristiques d’un vecteur sont sa direction, son sens et sa norme (sa longueur).
- Pour représenter un vecteur \(\overrightarrow{AB}\) on trace une flèche dont le point initial est \(A\) et l’extrémité est le point \(B\).
- Pour construire une somme de vecteurs, on représente le premier vecteur puis, à partir de l’extrémité de ce vecteur, on construit le deuxième. Le vecteur somme est défini par l’origine du premier vecteur et l’extrémité du second.







Démontrer avec des vecteurs
EX. 1


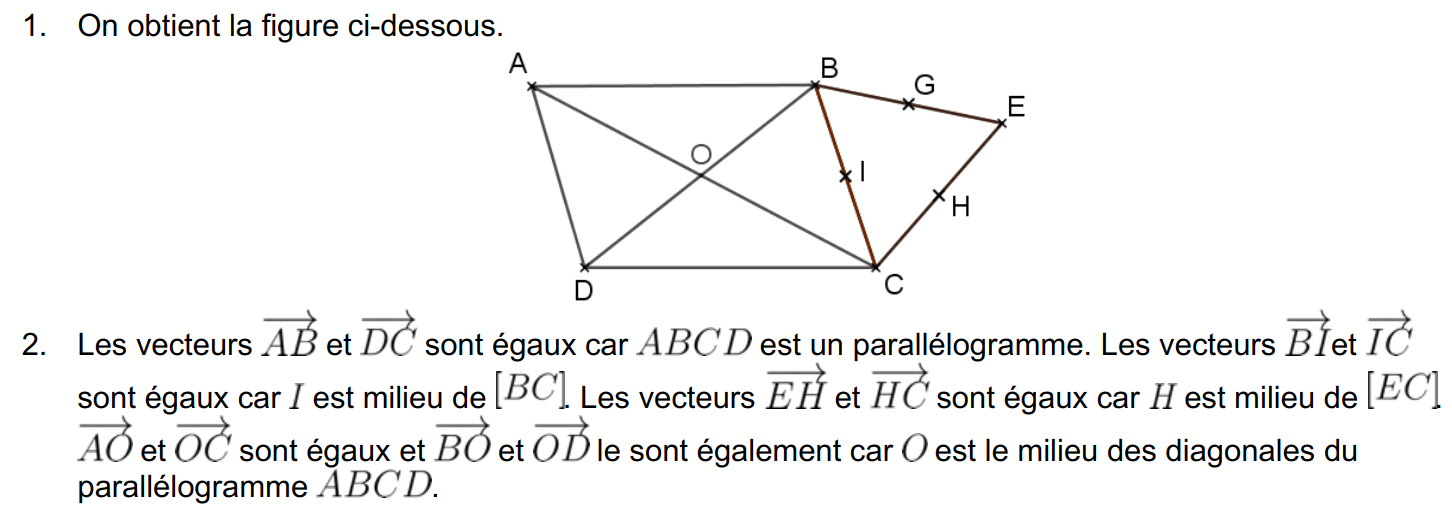
A
B
C
M
N
Construction des points :

A
B
C
M
N
A
B
C
M
N
A
B
C
M
N
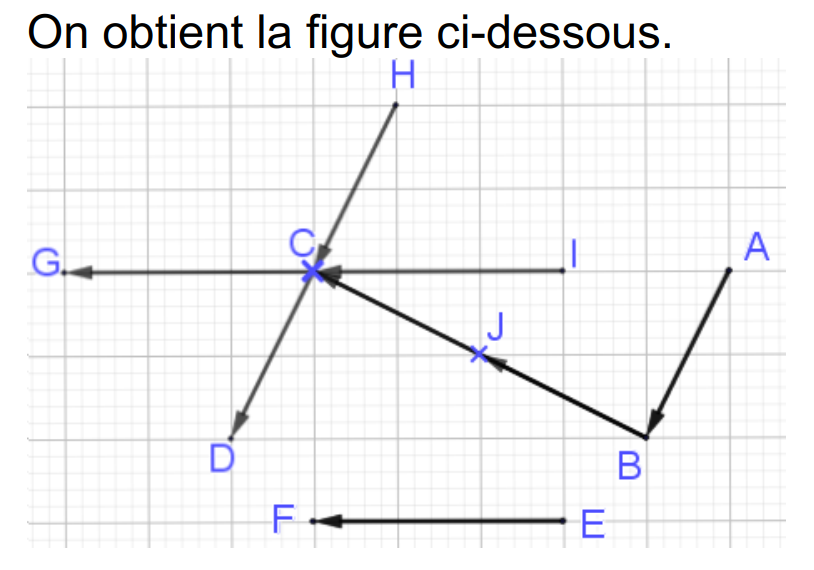
EX. 2




Règle du parallélogramme
Rq. Ici ABDC a un angle droit donc c'est un rectangle.


d'après la relation de Chasles.
On met les vecteurs "bout à bout"


d'après la relation de Chasles.
On met les vecteurs "bout à bout" à partir de A

On peut inverser les deux vecteurs dans une somme cela ne modifie pas le résultat
d'après la relation de Chasles.



On conjecture que le quadrilatère DEFG est un rectangle.
Nous allons utiliser les vecteurs pour montrer que ses diagonales se coupent en leur milieu, A.

On montre de la même façon
que donc que
A est aussi le milieu de [GE].
Les diagonales du quadrilatère DEFG se coupent en leur milieu donc DEFG est un parallélogramme.

On a vu que ABDC est un rectangle donc
Le parallélogramme DEFG a un angle droit donc c'est un rectangle.
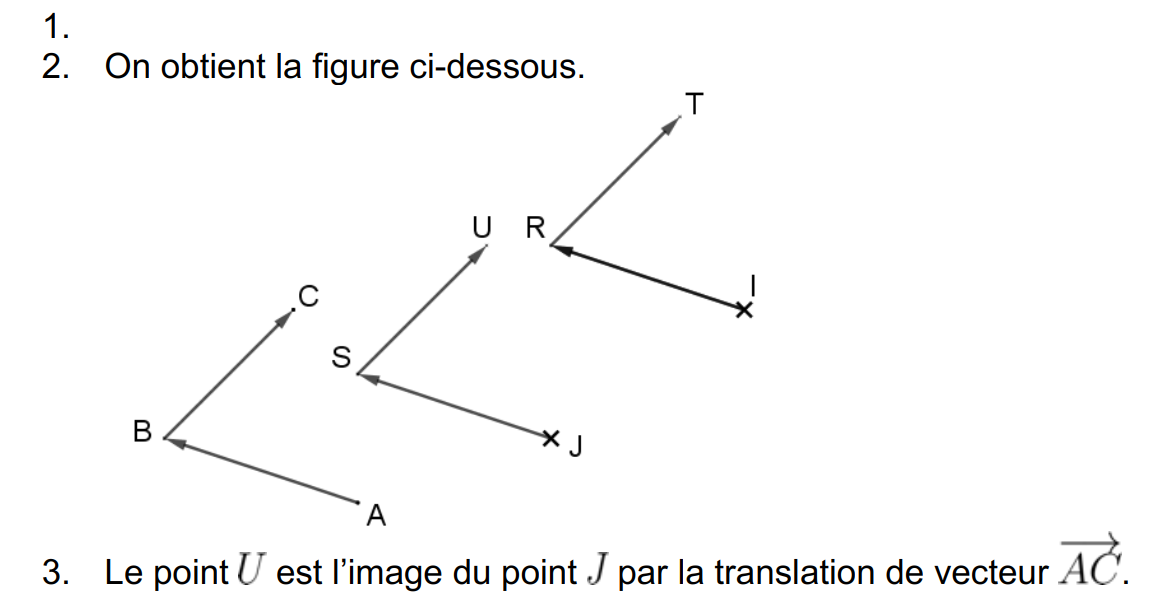
EX. 3
On va utiliser la relation de Chasles pour décomposer les vecteurs du premier membre de l'égalité afin de faire apparaître ceux du deuxième membre :
d'après la
relation de Chasles.
On a donc
d'après la relation de Chasles.
soit
donc
d'où


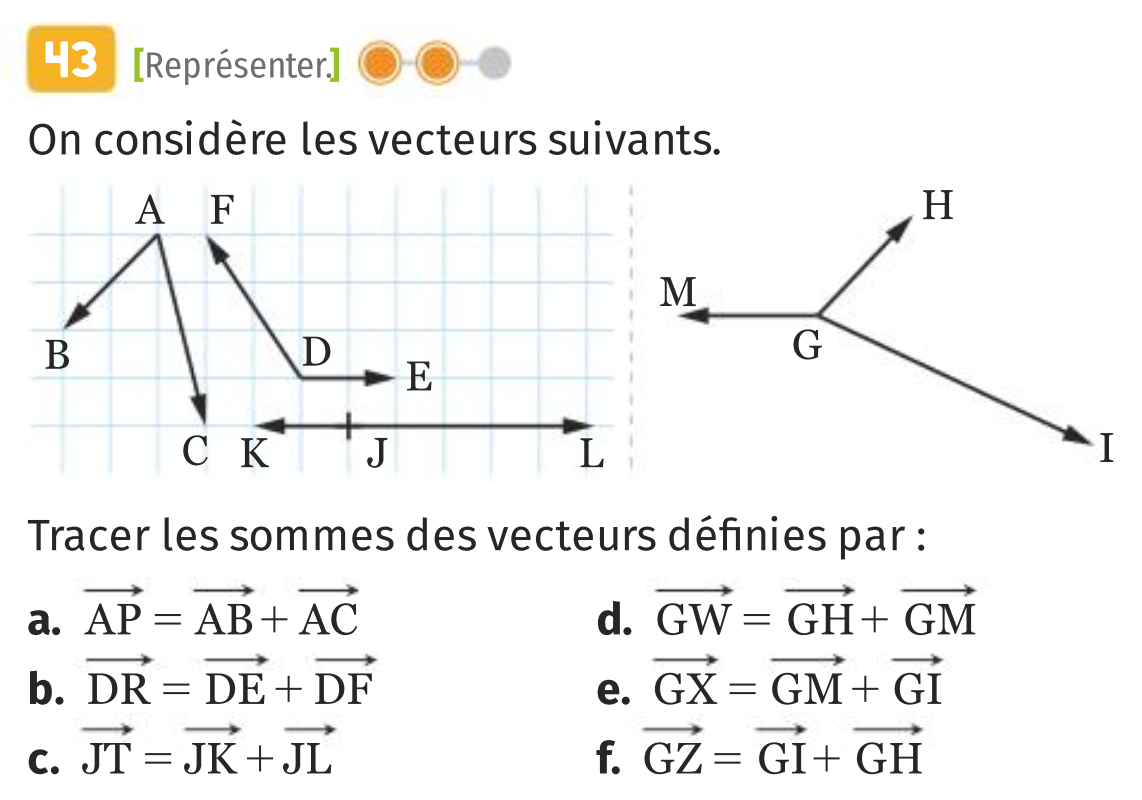
41 p 186
Exemple :

Exemple :

Exemple :


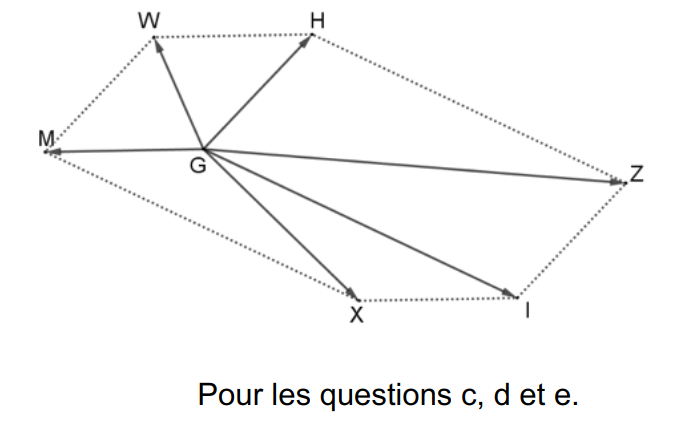
42 p 187



Géométrie
Repérée
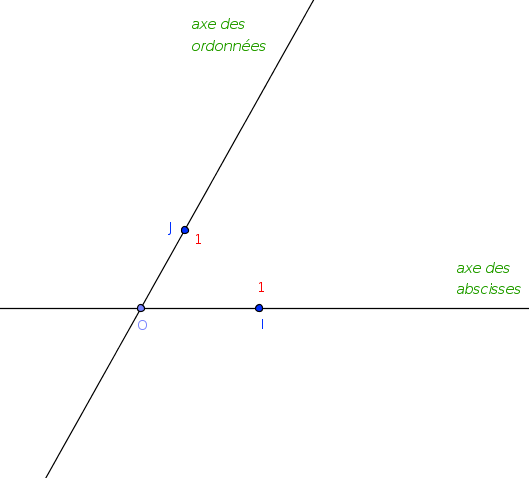
Un repère quelconque
Définir un repère du plan, c’est choisir 3 points non alignés dans un ordre précis : O, I, J.
On note ce repère (O, I , J)
(OI) :
(OJ) :
Origine du repère
Repères
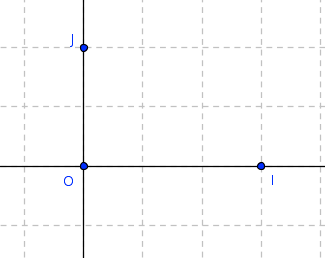
Repère orthogonal
Des repères particuliers :
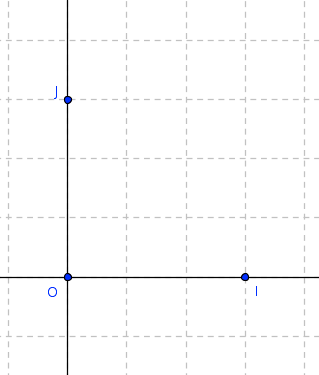
Repère orthonormé
(OI)⊥(OJ)
(OI)⊥(OJ) et OI = OJ
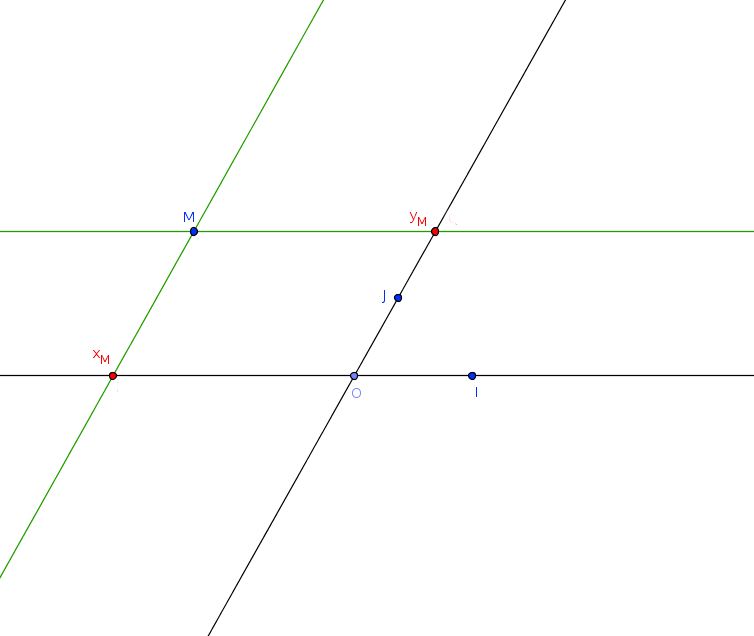
abscisse
du point M
ordonnée
du point M
(xM ; yM) : coordonnées du point M dans le repère (O, I , J).
Exemples : Dans le repère (O, I , J), on a :
O (0 ; 0) ; I (1 ; 0) ; J (0 ; 1) ; A (3 ; 2) ; B (−2 ; 3) et C (−1 ; −2).
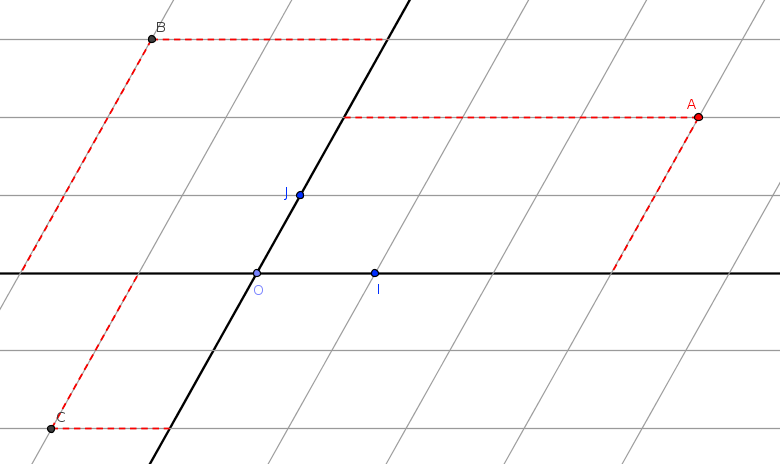
Coordonnées du milieu d’un segment
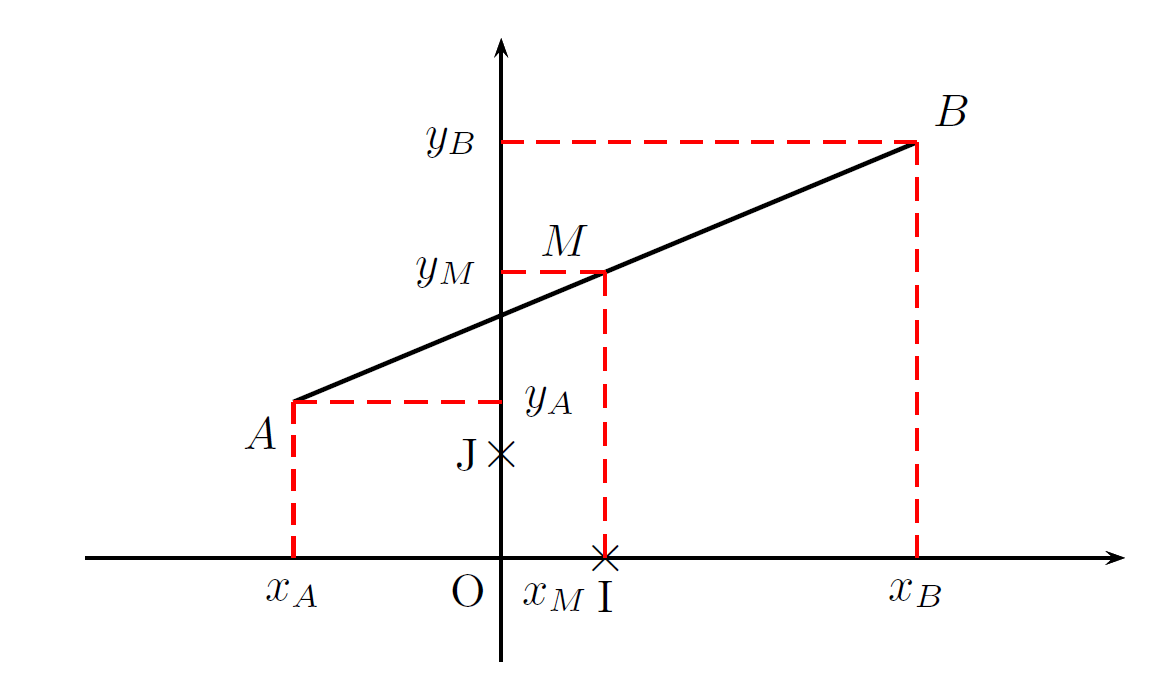
Coordonnées du milieu d’un segment
Soit (O, I , J) un repère du plan et A (xA ; yA) et B (xB ; yB) deux points du plan.
Les coordonnées du milieu M de [AB] sont :
et
Exemples :
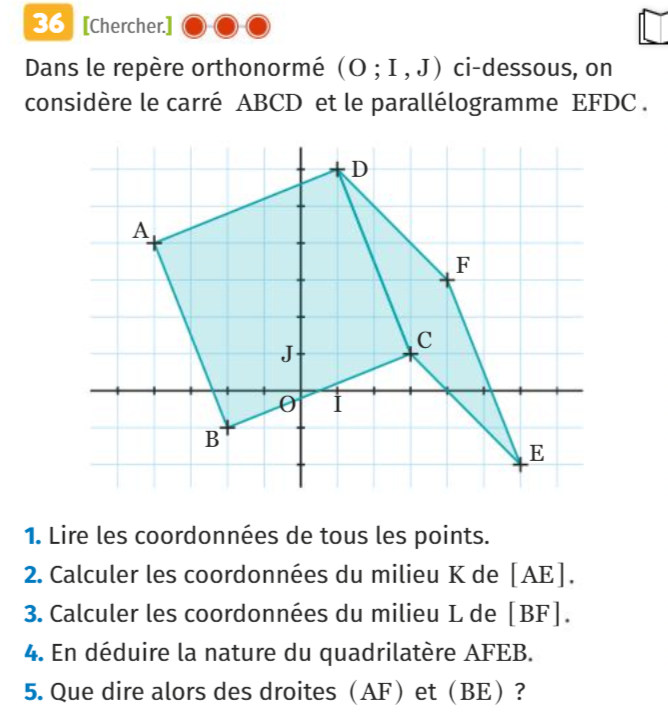
1) C(−5 ; 7) et E(9 ; −4) sont deux points du plan muni d'un repère (O ; I, J).
Calculer les coordonnées du milieu K du segment [CE].
et
et
et
Exemples :
2) M(−1 ; 3) et K(2 ; −3) sont deux points du plan muni d'un repère (O ; I, J).
Soit N le point du plan tel que K soit le milieu du segment [MN]. Calculer les coordonnées du point N.
et
et
et
Exemples :
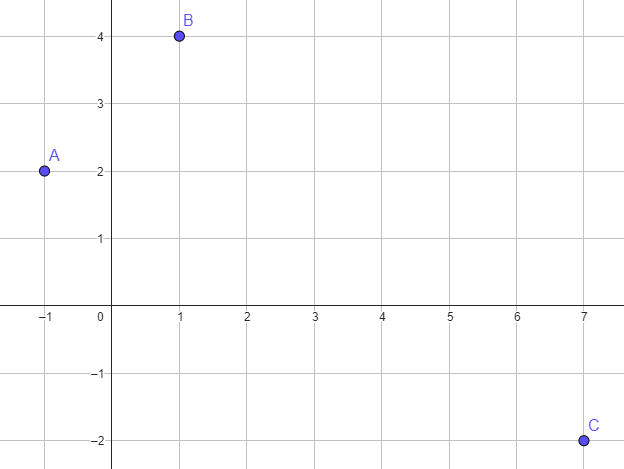
3) A(−1 ; 2), B(1 ; 4) et C(7 ; −2) sont trois points du plan muni d'un repère (O ; I, J).
Calculer les coordonnées du point D tel que ABCD soit un parallélogramme.
Étape 1:
On calcule les coordonnées de K, le milieu de [AC], diagonale du parallélogramme ABCD.
et
et
et
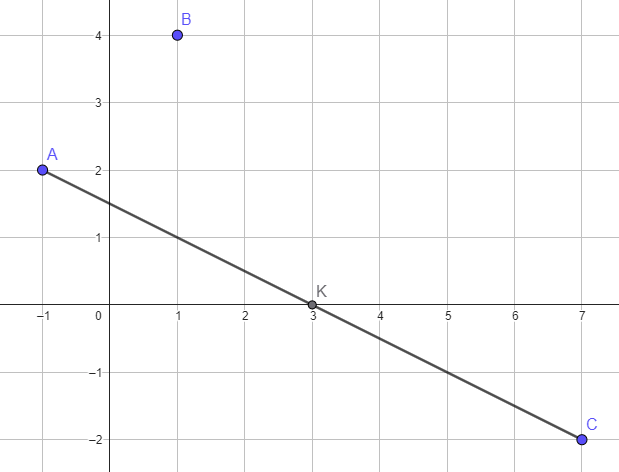
Étape 2:
K est aussi le milieu de la diagonale [BD], donc on a :
et
et
et
et
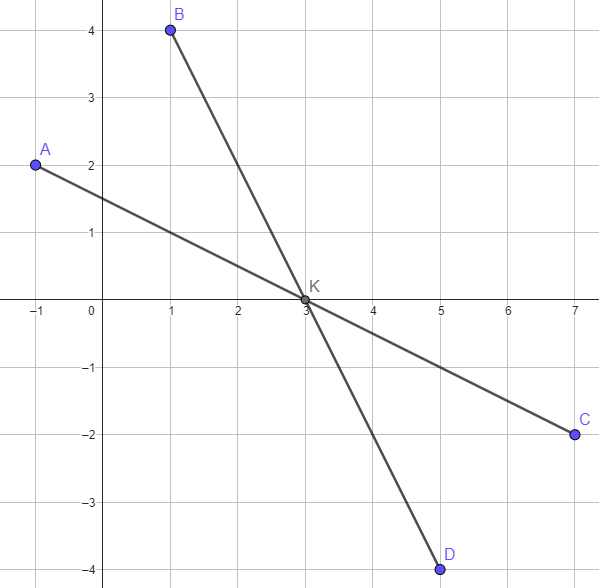

V
F
V
F




Vrai
Faux
Faux









(A, B et C uniquement)

et

Le point D est le symétrique du point A par rapport au point K si et seulement si le point K est le milieu de [AD] :
et
et
et

Les diagonales [BC] et [AD] du quadrilatère ABCD ont le même milieu K donc ABCD est un parallélogramme.




Distance
Soit (O, I , J) un repère orthonormé du plan.
A (xA ; yA) et B (xB ; yB) deux points du plan.
La distance AB vérifie :

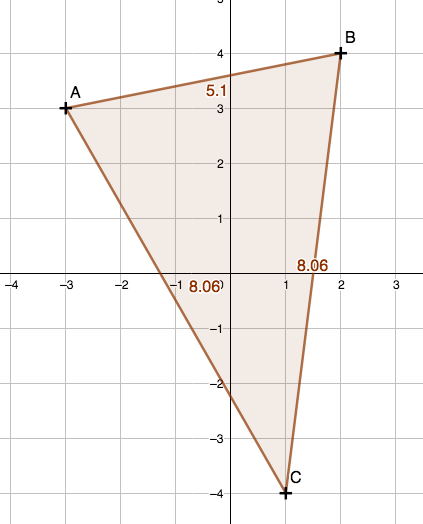
Le triangle ABC semble isocèle en C.

On calcule les distances AC et BC pour montrer qu'elles sont égales :

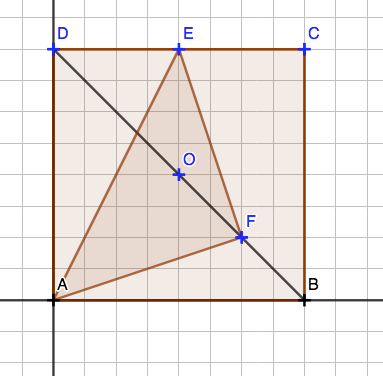
Dans le repère \( (A\;;B\;,D)\) on a :
Le repère étant orthonormé on peut utiliser la formule de calcul d’une distance :

D'après la question 3., \(EF=AF\) donc le triangle AEF est isocèle en F.
donc d'après la réciproque du théorème de Pythagore le triangle AEF est rectangle en F.
Conclusion : le triangle AEF est isocèle rectangle en F.


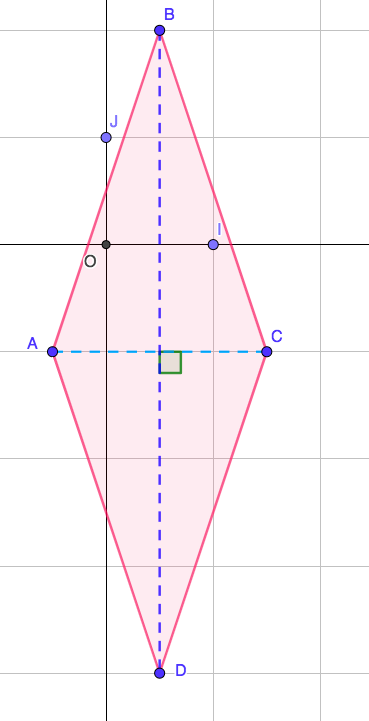
2. D’après la figure ci-contre, on peut conjecturer que le quadrilatère est un losange.
3. On peut montrer que [BD] et [AC] se coupent en leur milieu et que AB = BC...

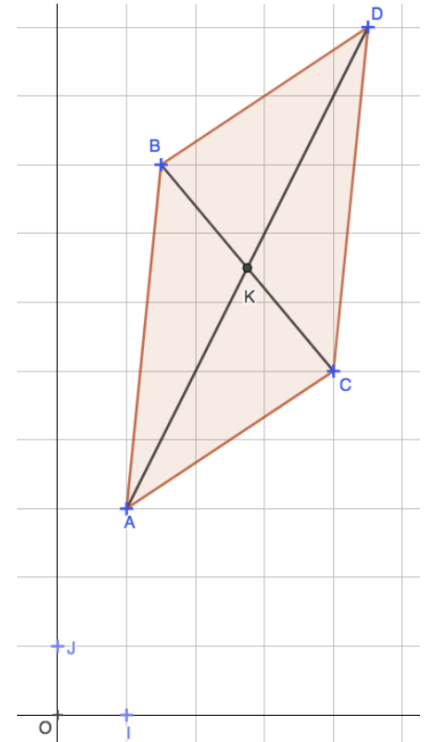
Les points K et L sont confondus donc le quadrilatère ABCD est un parallélogramme.
On a AB = BC ; Le parallélogramme ABCD a deux côtés consécutifs de même longueur donc c'est un losange.
Vecteurs
et coordonnées
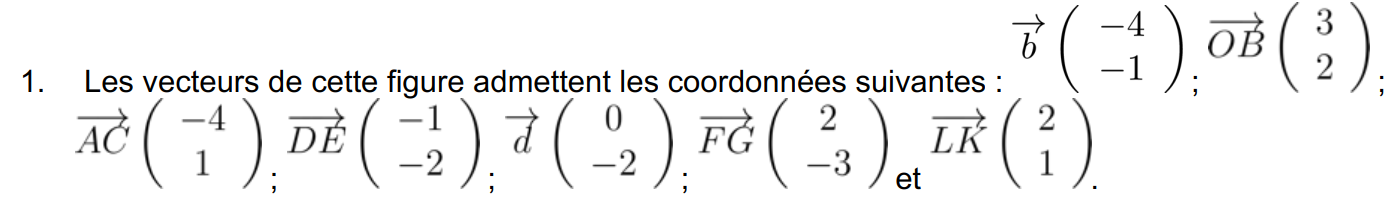


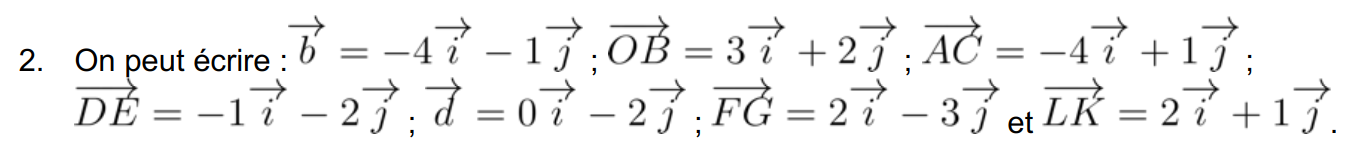









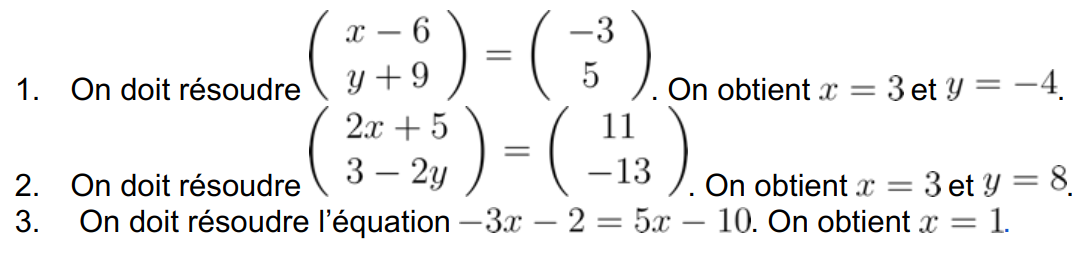


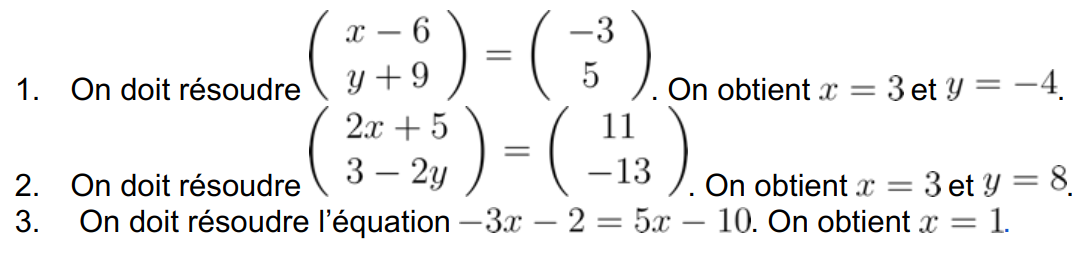

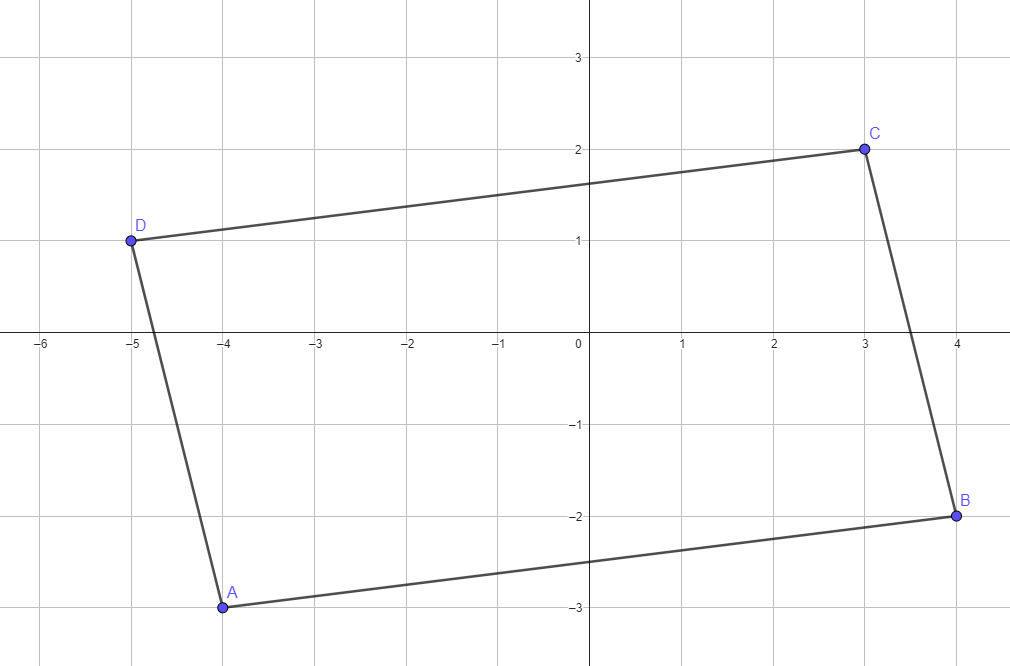
On conjecture que ABCD est un parallélogramme.


Pour le démontrer on va prouver que \( \overrightarrow{AB}=\overrightarrow{DC}\).


Pour le démontrer on va prouver que \( \overrightarrow{BC}=\overrightarrow{CE}\).

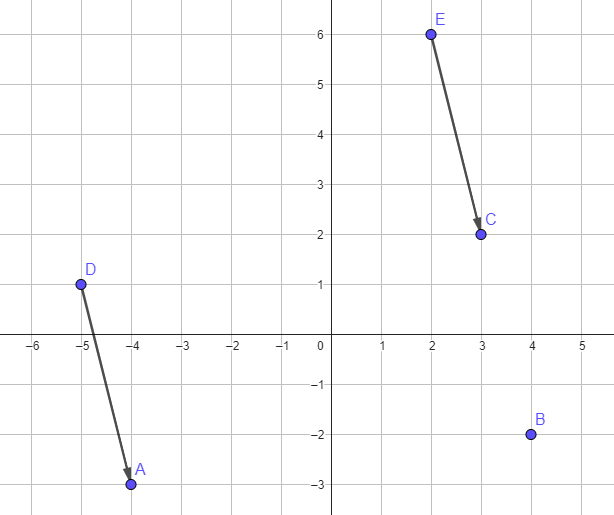
Pour le démontrer on va prouver que \( \overrightarrow{EC}=\overrightarrow{DA}\).