Automatismes : Fonctions
Séance 1
Question 1 :
Question 2 :
Question 3 :
Question 4 :
Question 5 :
Question 6 :
Question 7 :
Question 8 :
Question 9 :
Question 10 :
Question 11 :
Question 12 :

Question 13 :

Question 14 :

Question 15 :

Question 16 :

Question 17 :
Question 18 :
Question 19 :
Question 20 :
Automatismes : Fonctions
Séance 2
Question 1 :
Question 2 :
Question 3 :
Question 4 :
Question 5 :
Question 6 :
Question 7 :
Question 8 :
Question 9 :
Question 10 :
Question 11 :
Question 12 :

Question 13 :

Question 14 :

Question 15 :
Question 16 :

Question 17 :

Question 18 :
Question 19 :
Question 20 :
Automatismes : Fonctions
Séance 3



Question 1 :

(le domaine de définition des fonctions \(f\) et \(g\).)

Question 2 :


Question 3 :


Question 4 :

Hulk

Question 5 :

Question 6 :

Question 7 :

Question 8 :

Question 9 :

Question 10 :
Question 11 :



Question 12 :



Question 13 :



Question 14 :

Dresser le tableau de signes de chacune de ces fonctions.
Question 15 :

Dresser le tableau de variations de chacune de ces fonctions.
Automatismes : Fonctions
Séance 4
Question 1 :
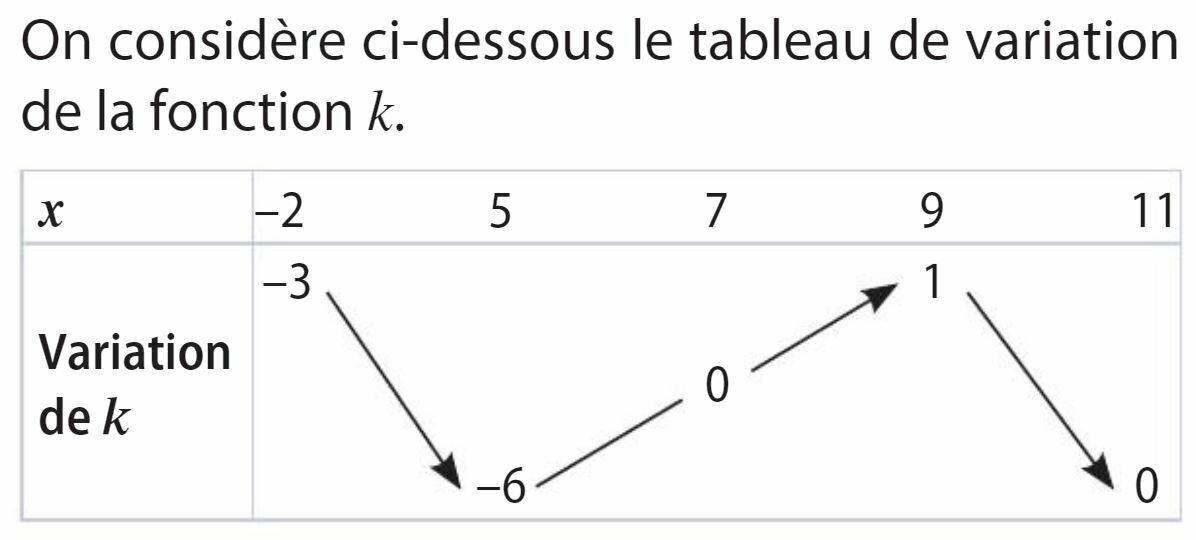
Quel est l'ensemble de définition de la fonction \(k\) ?
Question 2 :

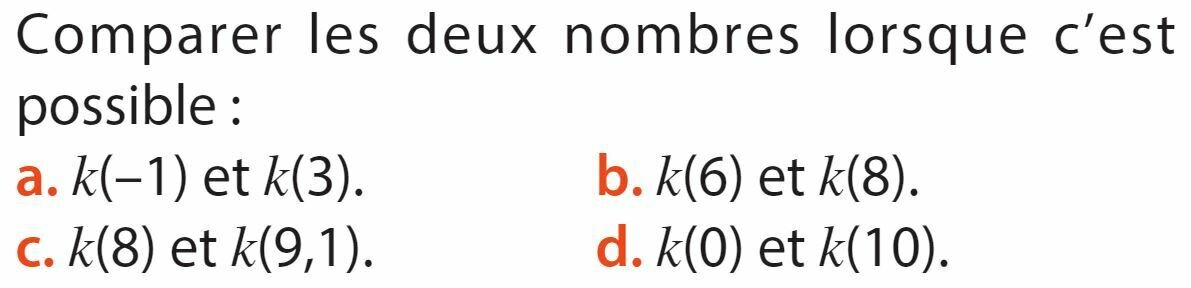
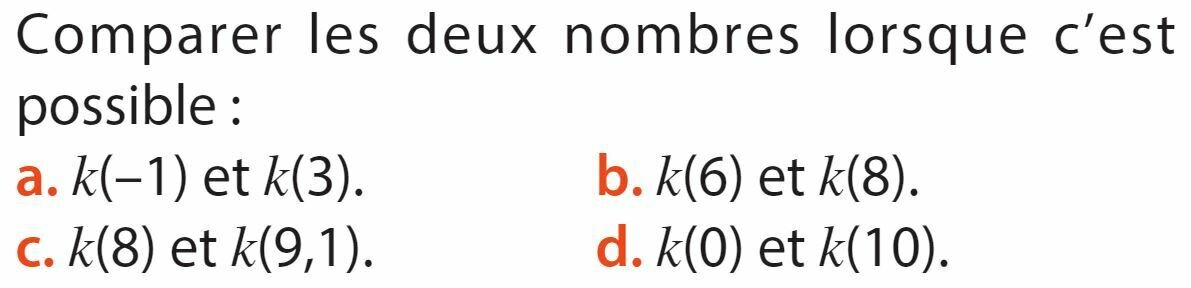
Question 3 :

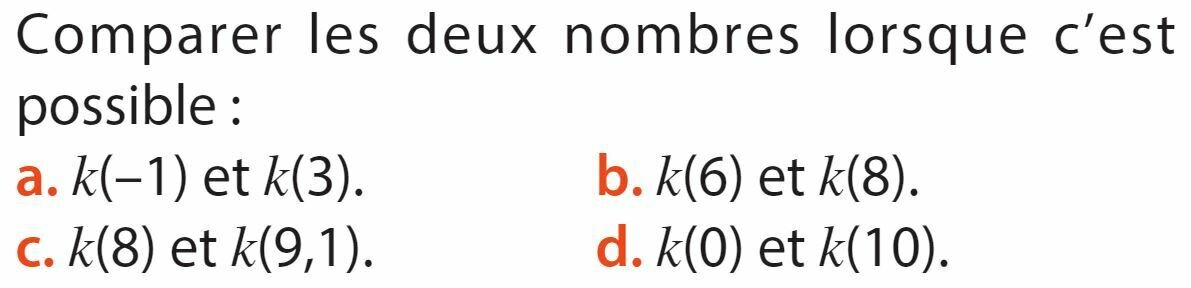
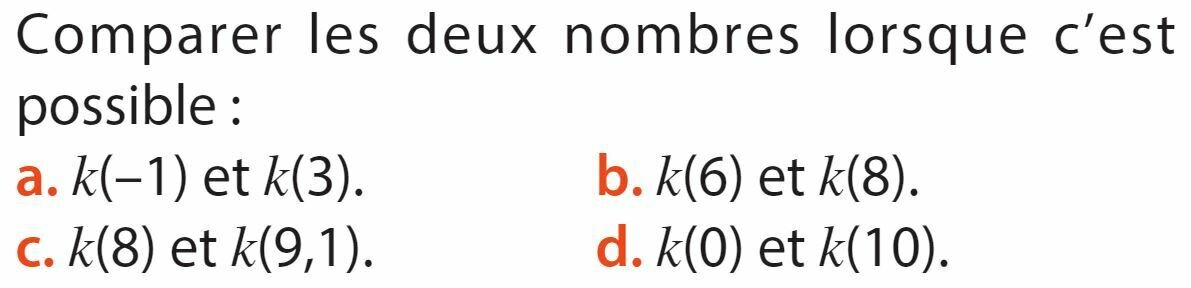
Question 4 :

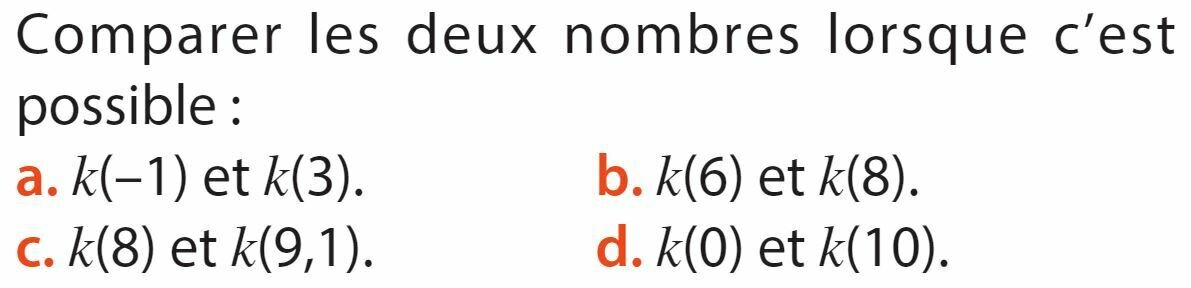
Question 5 :

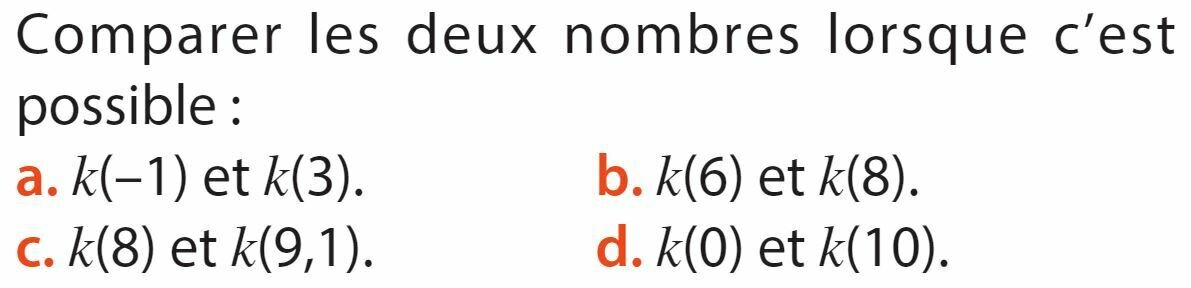
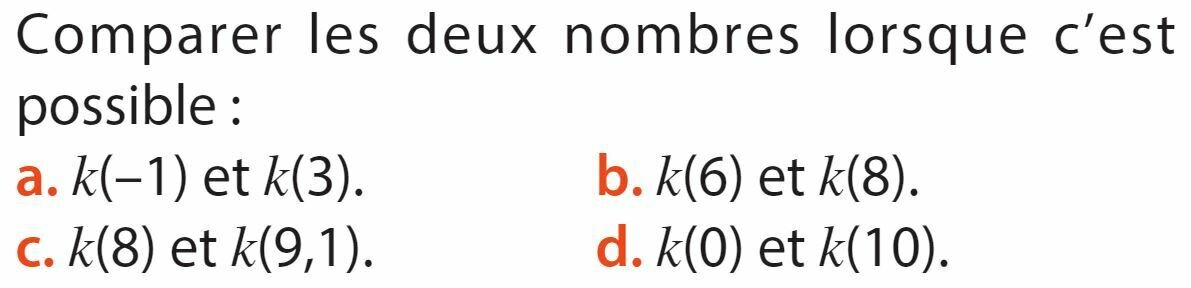
Question 6 :

Question 7 :

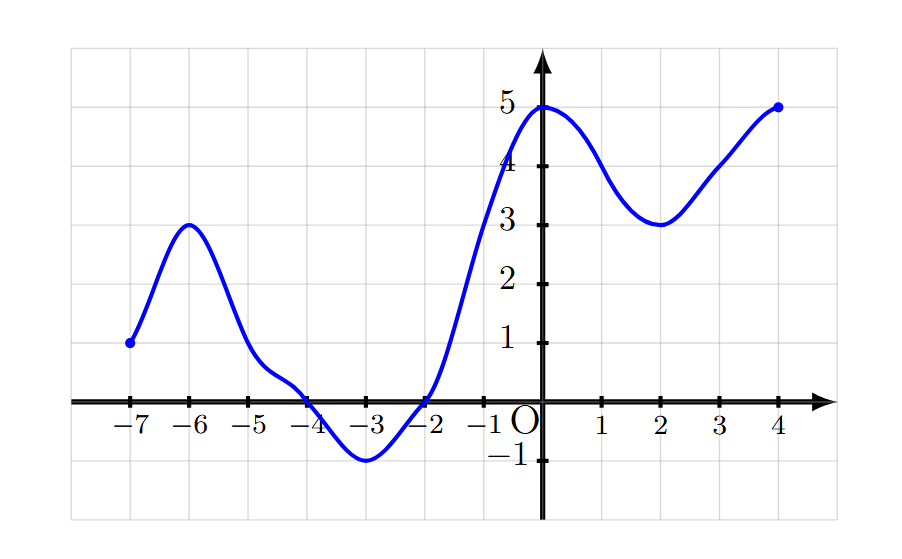
Quel est l'ensemble de définition de la fonction \(f\) ?
Question 8 :

Quel est le minimum de \(f\) sur son ensemble de définition ?
Question 9 :

Quel est le maximum de \(f\) sur son ensemble de définition ?
Question 10 :

Quel est le maximum de \(f\) sur l'intervalle \([-3~;~2]\) ?
Question 11 :

Quel est le minimum de \(f\) sur l'intervalle \([0~;~4]\) ?
Question 12 :

Donner le nombre de solutions de l'équation \(f(x)=0\).
Question 13 :



Question 14 :



Question 15 :



Question 16 :



Question 17 :



Question 18 :



Automatismes : Fonctions
Séance 5
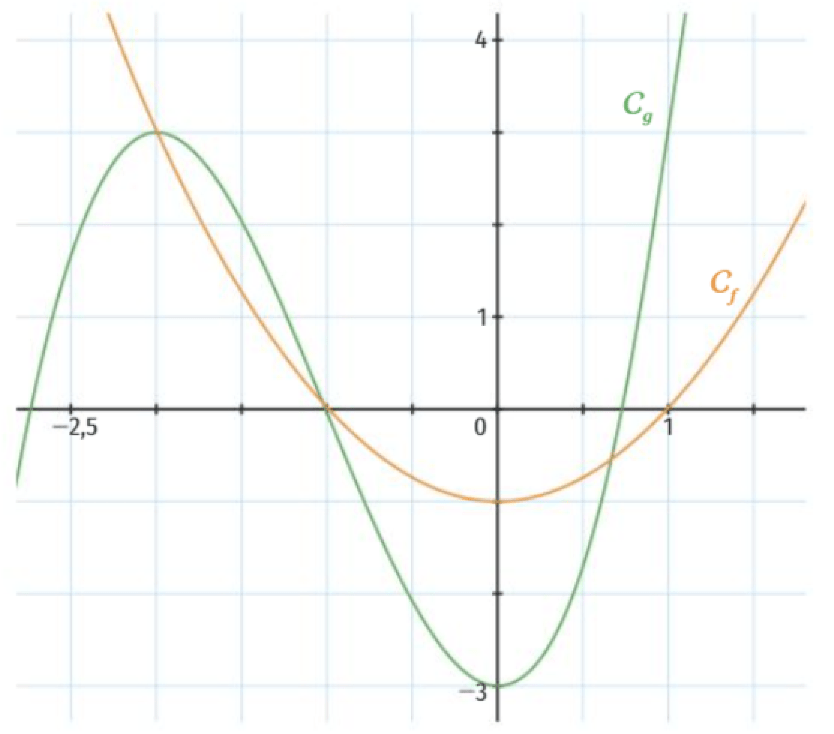
Question 1 : Résoudre l'équation \(g(x)=3\)

Question 1 : Il s'agit de trouver les antécédents de 3 par \(g\)
3

3
Question 2 : Résoudre \(g(x)>3\)

3
Question 2 : Quels sont les réels \(x\) ayant une image par la fonction \(g\) strictement supérieure à \(3\).

3
Question 3 : Déterminer les extremums de la fonction \(g\) sur \([-2~;~1]\).

Question 3 : Déterminer les extremums de la fonction \(g\) sur \([-2~;~1]\).

Question 4 : Résoudre graphiquement l'inéquation \(g(x)\geqslant 0\).

Question 4 : Il s'agit de déterminer les réels \(x\) qui ont une image positive par \(g\).

Question 5 : Résoudre graphiquement l'inéquation \(f(x)<0\).

Question 5 : Il s'agit de déterminer les réels \(x\) qui ont une image strictement négative par \(f\).

Question 6 : Résoudre graphiquement l'inéquation \(f(x)\leqslant g(x)\).

Question 6 : Il s'agit de déterminer les abscisses \(x\) des points de \(C_f\) qui sont en-dessous de \(C_g\).
Question 7 :
Question 8 :
Question 9 :
Question 10 :
Question 11 :

2 a pour image par \(f\) :
Question 12 :

4 a pour image par \(f\) :
\(f\) est définie sur \([-3~;~3]\) donc 4 n'a pas d'image par \(f\).
Question 13 :

Des antécédents de 2 par \(f\) sont :
Question 14 :

Des antécédents de 3 par \(f\) sont :
Question 15 :
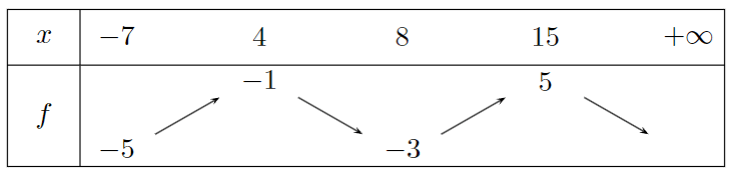
Le maximum de \(f\) sur \([-7~;~+\infty[\) est :
Question 16 :

Le minimum de \(f\) sur \([-7~;~+\infty[\) est :
Question 17 :

Le minimum de \(f\) sur \([-7~;~20]\) est :
On ajoute que \(f(20)=2\).
Question 18 :

\(f\) est décroissante sur :
Question 19 :

\(f\) est croissante sur :
Question 20 :

On peut affirmer que :
Question 21 :

Pour tout \(x\in[4~;~15]\), \(f(x)\) appartient à :
Quels sont les extremums de \(f\) sur \([4~;~15]\) ?
\(f(x) \in [-3~;~5]\)
Automatismes : Fonctions
Séance 6
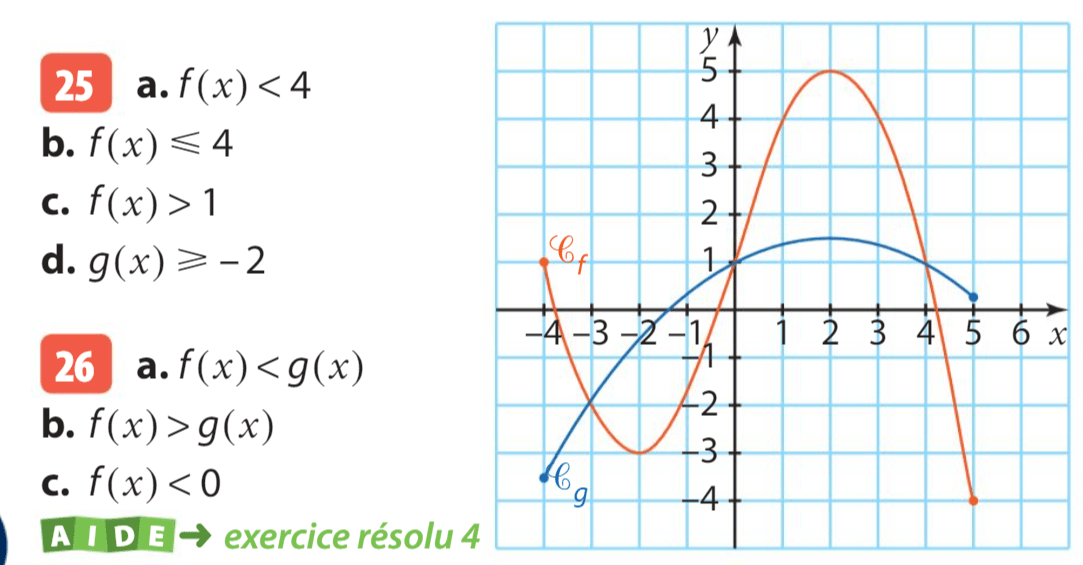
Question 1 :

Question 2 :

Question 3 :

Question 4 :

Question 5 :

Question 6 :
Question 7 :

Question 8 :

Question 9 :

Question 10 :

Question 11 :

Question 12 :