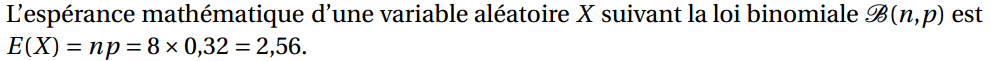Révisions pour le BAC

Mode examen :

Amérique du nord 2016

Ex 3 : QCM

1) \frac{20-15}{50-10}= \frac{1}{8}
2) (1-\frac{t}{100})^2=0,5 \Leftrightarrow 1-\frac{t}{100}=\sqrt{0,5} \Leftrightarrow t=100(1-\sqrt{0,5})

4. Lors d’un sondage, 53,5 % des personnes interrogées ont déclaré qu’elles voteront pour le candidat A aux prochaines élections. L’intervalle de confiance au seuil de 95 % donné par l’institut de sondage est [51 % ; 56 %]. Le nombre de personnes qui ont été interrogées est alors :

a. 40      b. 400      c. 1 600      d. 6 400

\frac{2}{\sqrt{n}}= 0,05\Leftrightarrow \frac{\sqrt{n}}{2}= 20\Leftrightarrow \sqrt{n}=40\Leftrightarrow n=40^2

Ex 4 : Fonctions

c.

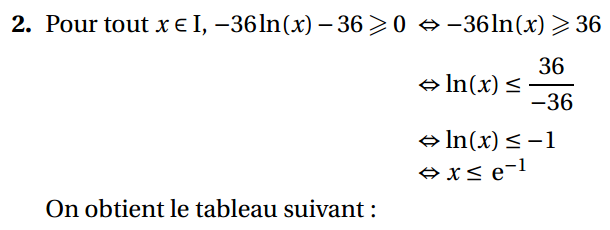
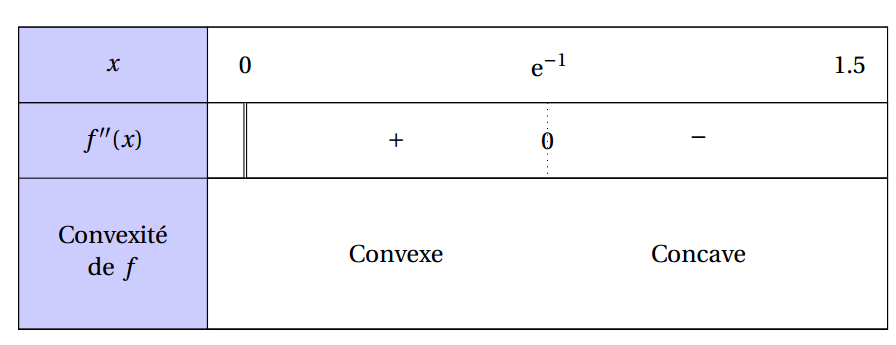
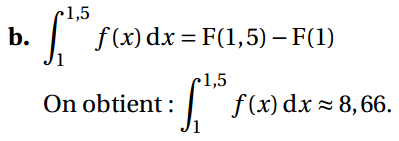
Amérique du nord 2016

Ex 2 : Suites

Une société propose un service d’abonnement pour jeux vidéo sur téléphone mobile. Le 1er janvier 2016, on compte 4 000 abonnés. À partir de cette date, les dirigeants de la société ont constaté que d’un mois sur l’autre, 8 % des anciens joueurs se désabonnent mais que, par ailleurs, 8 000 nouvelles personnes s’abonnent.

Diminuer de 8% revient à multiplier par 0,92. On obtient donc le nombre d’abonnés au 1er février 2016 en effectuant le calcul suivant : 4000 × 0,92 + 8000 = 11680.

Le nombre d’abonnés au 1er février 2016 est de 11 680.

1. Calculer le nombre d’abonnés à la date du 1er février 2016.

2. On considère l’algorithme suivant : 

Pour la suite de l’exercice, on modélise cette situation par une suite numérique (un) où un représente le nombre de milliers d’abonnés au bout de n mois après le 1er janvier 2016. La suite (un) est donc définie par :

u0 = 4 et, pour tout entier naturel n, un+1 = 0,92un +8.

3. On considère la suite (vn) définie pour tout entier naturel n par vn = un −100.

a. Montrer que la suite (vn) est géométrique de raison 0,92 et calculer son premier terme v0.

Pour tout entier naturel n,

v_{n+1} = u_{n+1} - 100
v_{n+1} = 0,92u_n+8 - 100
v_{n+1} = 0,92u_n-92
v_{n+1} = 0,92(u_n-\frac{92}{0,92})
v_{n+1} = 0,92(u_n-100)
v_{n+1} = 0,92v_n

La suite (vn) est donc bien une suite géométrique de raison q = 0,92.

v_0 = u_0- 100=4-100=-96

Son premier terme est v0 = −96.

b. Donner l’expression de vn en fonction de n.

v_n =(-96)\times 0,92^n

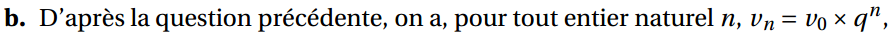
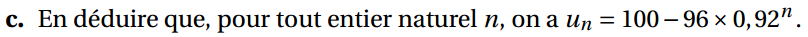
Soit

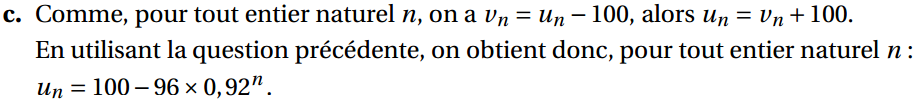
4. En résolvant une inéquation, déterminer la date (année et mois) à partir de laquelle le nombre d’abonnés devient supérieur à 70 000.

On cherche le premier entier naturel n vérifiant un > 70.

100-96\times0,92^n> 70
-96\times0,92^n>-30
0,92^n<\frac{-30}{-96}

On divise par un nombre négatif, le sens de l'inégalité change !

0,92^n<0,3125
ln(0,92^n) < ln (0,3125)
n\;ln(0,92) < ln (0,3125)
n> \frac{ln (0,3125)}{ln(0,92)}

On divise par un nombre négatif, le sens de l'inégalité change !

\frac{ln (0,3125)}{ln(0,92)}\approx13,95.

Le premier entier qui convient est donc 14.

C’est donc au 1er mars 2017 que la nombre d’abonnés deviendra supérieur à 70 000.

Polynésie 2016

Ex 2 : Suites

 u1 = 5000, or u1 = a × u0 + b = b car u0 = 0 donc b = 5000

b. En supposant de plus que u2 = 11000, montrer que pour tout entier naturel n, on a : un+1 = 1,2 × un +5000.

u2 = 11000, et u2 = a × u1 + b = a × u1 + 5000 donc

11000 = a × 5000 + 5000 d’où a = (11000 - 5000)/5000 = 1,2

Donc, pour tout entier n, on a : un+1 = 1,2 × un +5000.

2. a. Calculer u3 et u4.

   b. En 2013 et 2014, l’entreprise a vendu respectivement 18 000 et 27 000 écrans 3D. La modélisation semble-t-elle pertinente ?

Dans toute la suite, on fait l’hypothèse que le modèle est une bonne estimation du nombre d’écrans 3D que l’entreprise va vendre jusqu’en 2022.

a. u3 = 1,2 × u2 + 5000 = 18200 ; u4 = 1,2 × u3 +5000 = 26840.

b. En 2013 et 2014, l’entreprise a vendu respectivement 18 000 et 27 000 écrans 3D. La modélisation semble pertinente car u3 ≃ 18000 et u4 ≃ 27000.

3. On considère la suite (vn) définie pour tout entier naturel n par :

vn = un +25000.

a. Démontrer que la suite (vn) est une suite géométrique de raison 1,2. Préciser la valeur de son premier terme v0.

Pour tout entier naturel n, vn+1 = un+1 + 25000

                                                      = 1,2un + 5000 + 25000

                                                      = 1,2un + 30000

                                                      = 1,2(un + 30000/1,2)

                                                      = 1,2(un + 25000)

                                                vn+1 = 1,2vn

La suite (vn)n∈N est donc bien une suite géométrique de raison q = 1,2.

v0 = u0 +25000 = 25000 Son premier terme est v0 = 25000.

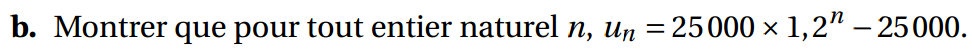
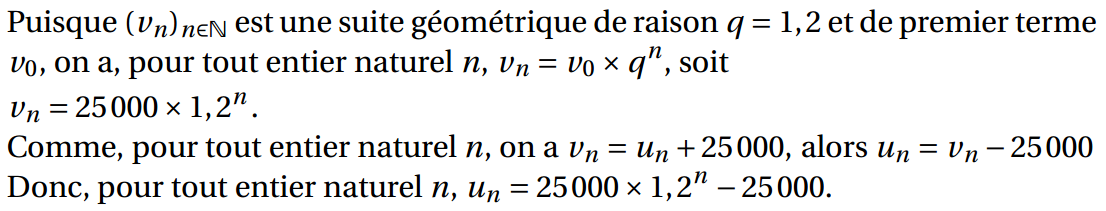
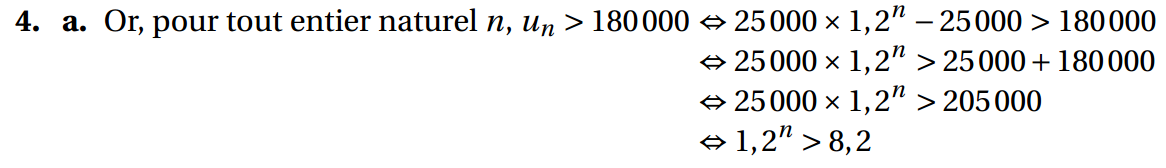
Résoudre l'inéquation :

1,2^n>8,2\Leftrightarrow ln1,2^n>ln8,2
\Leftrightarrow nln1,2>ln8,2
\Leftrightarrow n>\dfrac{ln8,2}{ln1,2}
\dfrac{ln8,2}{ln1,2}\approx 11,54
n\geq12

1

W\leq8,2

n prend la valeur n+1

n

n = 12

d. À partir de 2023, l’entreprise prévoit une baisse de 15 % par an du nombre de ses ventes d’écrans 3D. Combien d’écrans 3D peut-elle prévoir de vendre en 2025 ?

Asie 2016

Ex 2 (Partie A) : proba. 

Dans ce qui suit, les résultats approchés sont à arrondir au millième.

Une entreprise produit en grande série des clés USB pour l’industrie informatique. On prélève au hasard 100 clés dans la production de la journée pour vérification. La production est assez grande pour que l’on puisse assimiler ce prélèvement à un tirage avec remise de 100 clés.

On admet que la probabilité qu’une clé USB prélevée au hasard dans la production d’une journée soit défectueuse est égale à 0,015.

On considère la variable aléatoire X qui, à tout prélèvement ainsi défini, associe le nombre de clés défectueuses de ce prélèvement. 

1. Justifier que la variable aléatoire X suit une loi binomiale dont on déterminera les paramètres.

Le prélèvement d'une clé, est une expérience aléatoire à deux issues : la clé est défectueuse, avec une probabilité p = 0,015, ou elle n’est pas défectueuse, avec la probabilité 1− p.

C'est une épreuve de Bernoulli.

La production est assez grande pour que l’on puisse assimiler le prélèvement de 100 clés à un tirage avec remise.

Il s'agit de la répétition de 100 épreuves de Bernoulli identiques et indépendantes. C'est un schéma de Bernoulli.

La variable aléatoire X qui donne le nombre de clés défectueuses dans le lot de 100 clés suit donc la loi binomiale de paramètres n = 100 et p = 0,015.

2. Calculer les probabilités p(X = 0) et p(X = 1).

Avec une TI : 2de - var (distrib) binomFdp

Avec une CASIO : menu STAT - F5 (DIST) - F5(BINM) - F1 (BPD) Réglages : Data : Variable ; x : 0 (puis 1) ; Numtrial : 100 ; p : 0.015

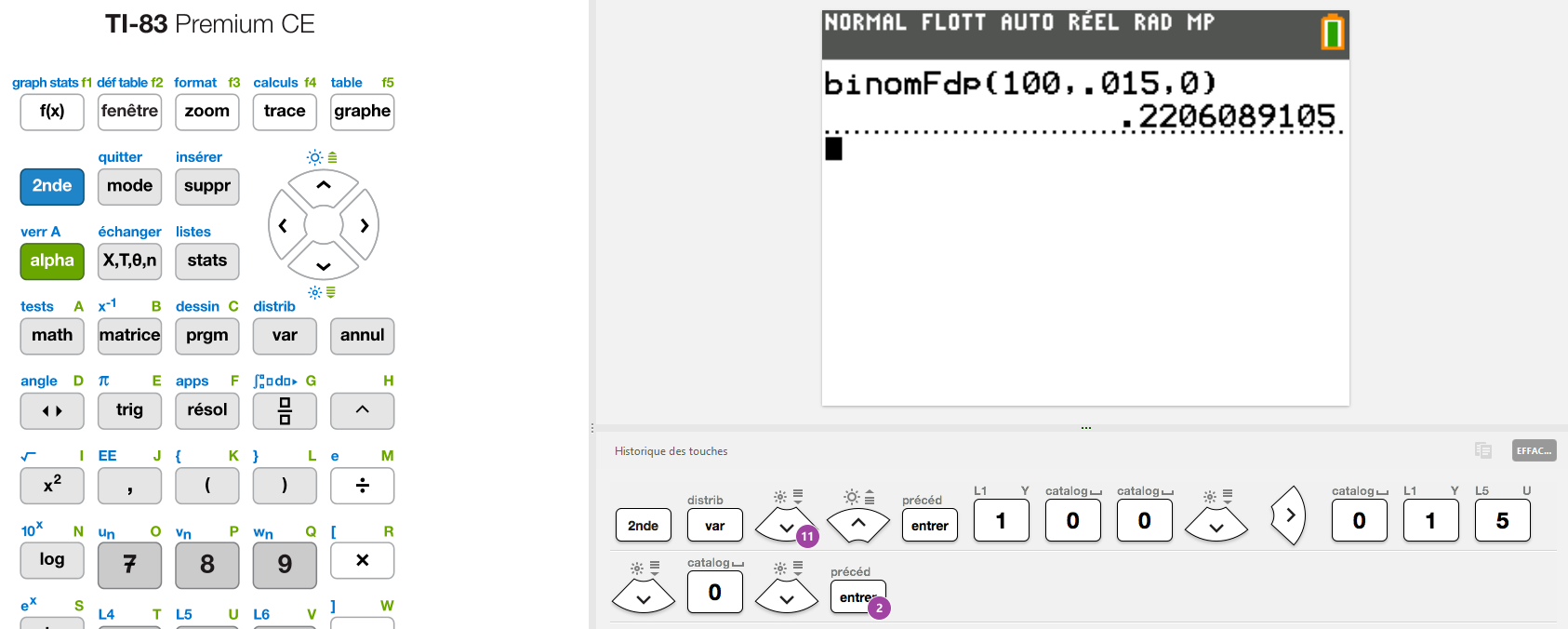
p(X = 0) ≈ 0,221

p(X = 1) ≈ 0,336

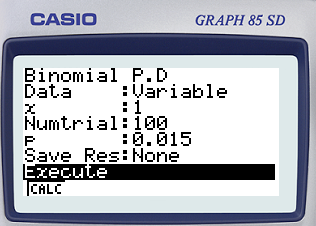
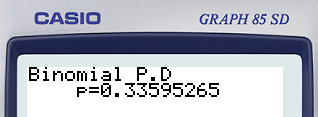
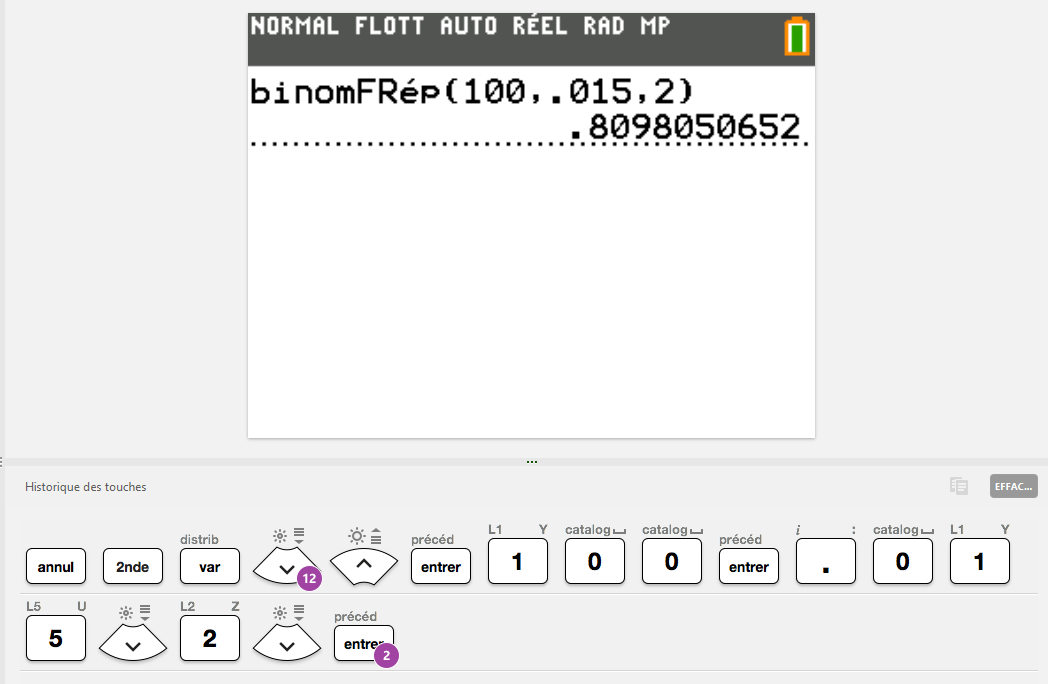
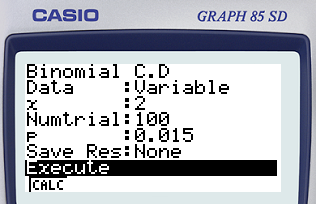
3. Calculer la probabilité que, dans un tel prélèvement, au plus deux clés soient défectueuses.

On doit déterminer  : 

p(X\leq 2)

Avec une TI : 2de - var (distrib) binomFRép

Avec une CASIO : menu STAT - F5 (DIST) - F5(BINM) - F2 (BCD) Réglages : Data : Variable ; x : 2 ; Numtrial : 100 ; p : 0.015

p(X\leq 2) \approx 0,810

Amsud nov 2016

Ex 1 (3) : proba. 

NB : p(X<2)=p(X\leq2)-p(X=2)
= p(X=0) + p(X=1)
p(X\geq2)=1-p(X<2)

Liban mai 2015

Ex 3 (partie A) : proba. 

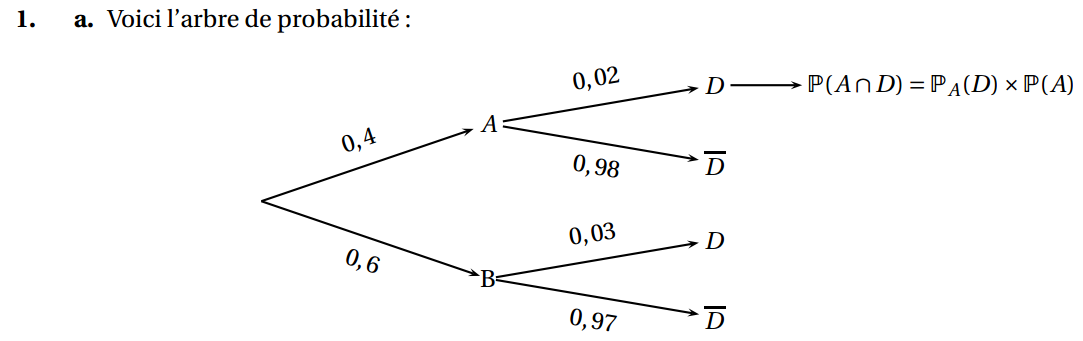
b. Montrer que la probabilité qu’une médaille soit défectueuse est égale à 0,026.

c. Calculer la probabilité qu’une médaille soit produite par la machine MA sachant qu’elle est défectueuse.

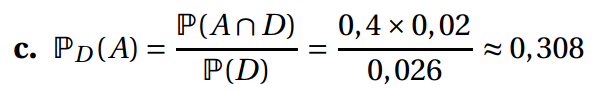
2. Les médailles produites sont livrées par lots de 20. On prélève au hasard un lot de 20 médailles dans la production. On suppose que la production est assez importante pour que l’on puisse assimiler ce prélèvement à un tirage aléatoire avec remise. Les tirages sont supposés indépendants. On note X la variable aléatoire prenant pour valeur le nombre de médailles défectueuses contenues dans ce lot.

a. Préciser la loi que suit X et donner ses paramètres.

b. Calculer la probabilité qu’il y ait au plus une médaille défectueuse dans ce lot.

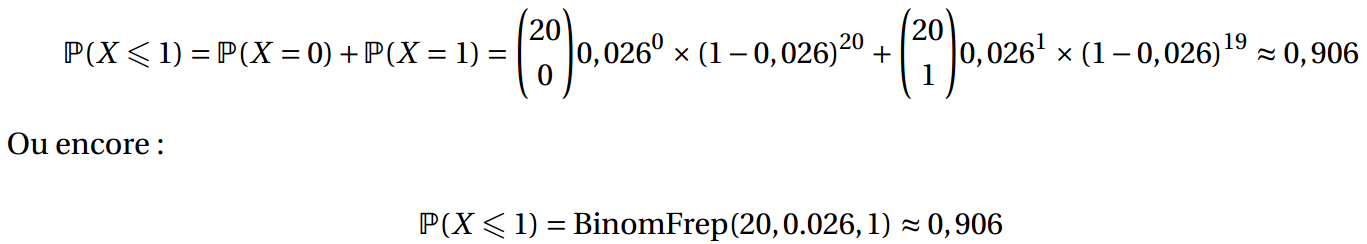
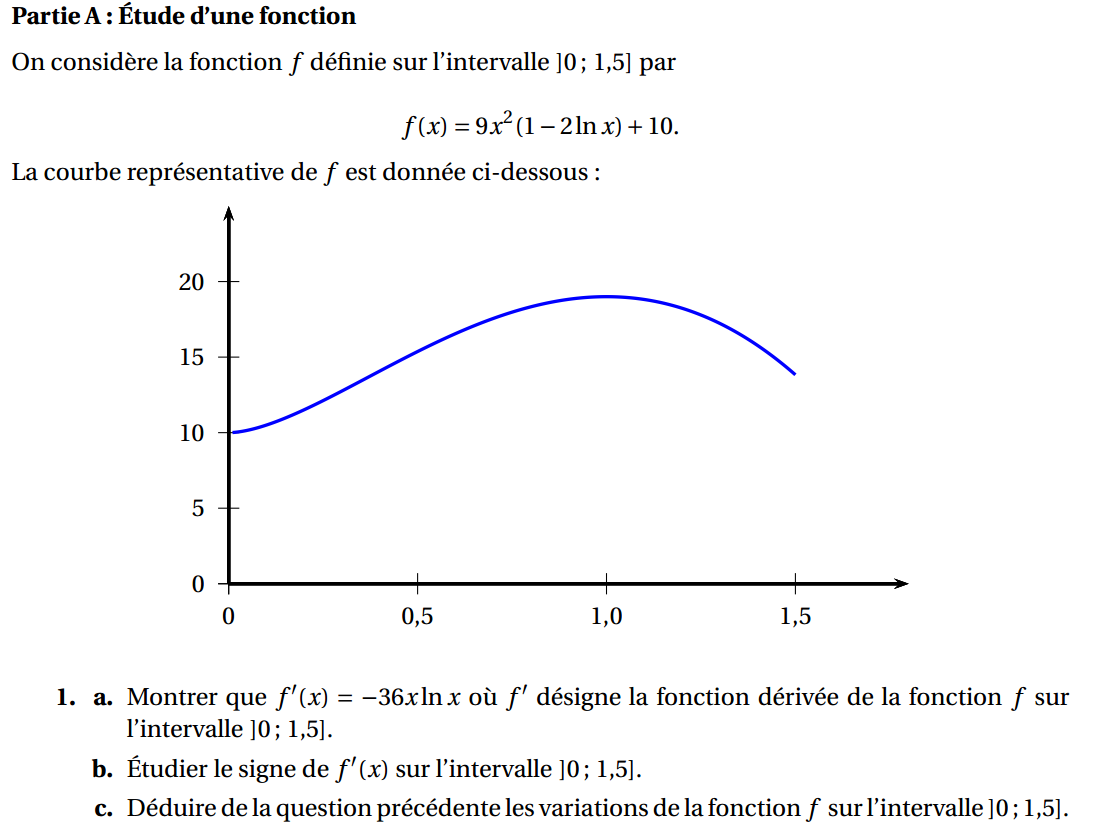
Une entreprise artisanale produit des parasols. Elle en fabrique entre 1 à 18 par jour. Le coût de fabrication unitaire est modélisé par une fonction f définie et dérivable sur l’intervalle [1 ; 18].

On note x le nombre de parasols produits par jour et f (x) le coût de fabrication unitaire exprimé en euros.

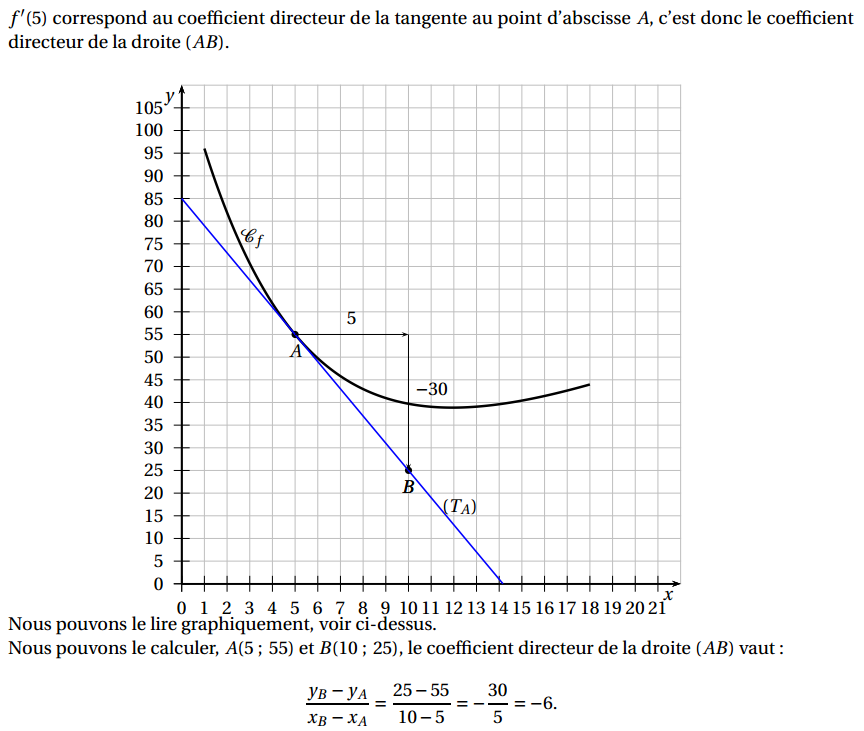
Dans le repère orthogonal ci-après, on a tracé la courbe représentative C de la fonction f et la tangente TA au point A(5 ; 55). Le point B(10 ; 25) appartient à la tangente TA.

On admet que :

Ex 2 : Fonctions 

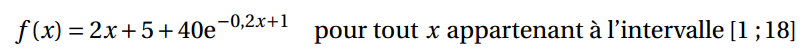
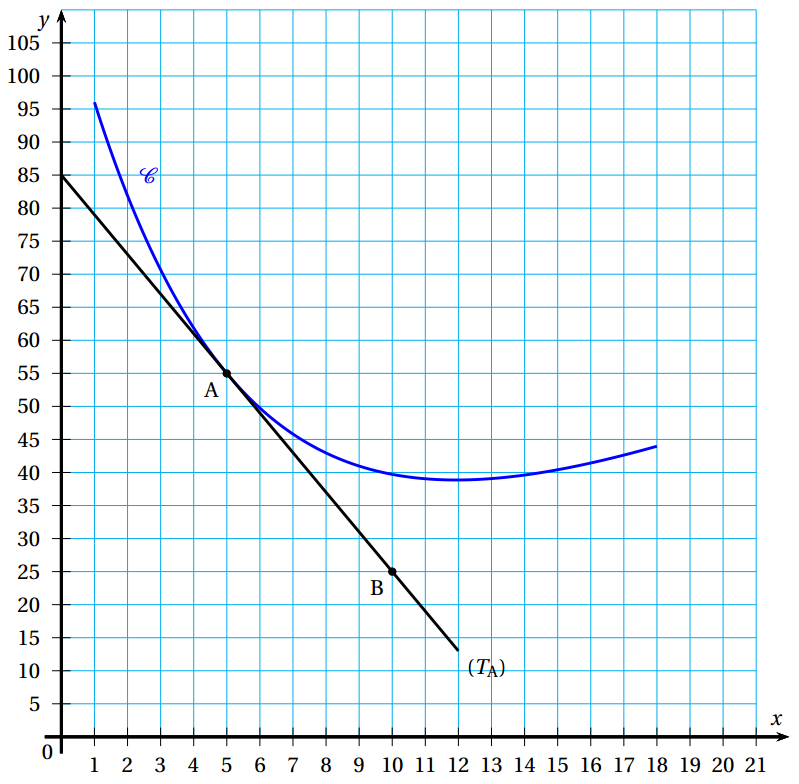
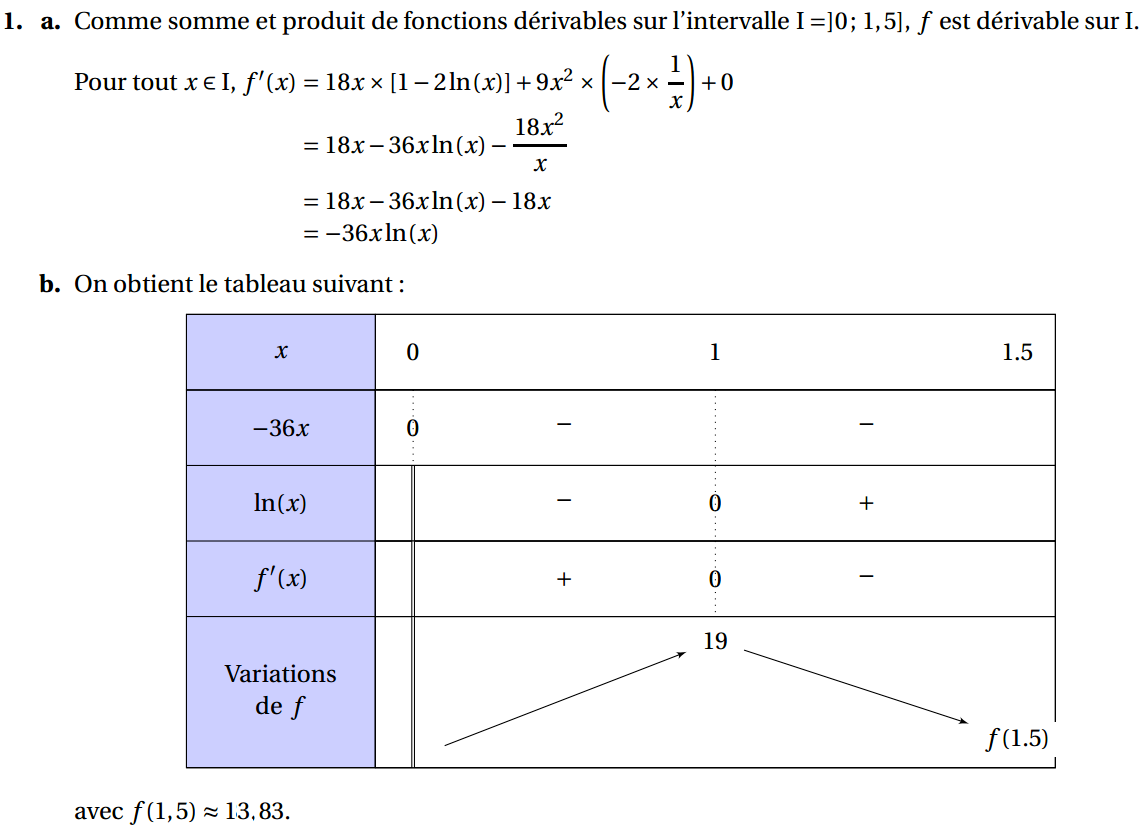
1. a. Déterminer graphiquement la valeur de f ′ (5) en expliquant la démarche utilisée.

b. Déterminer l’expression de f'(x) pour tout x appartenant à l’intervalle [1 ; 10].

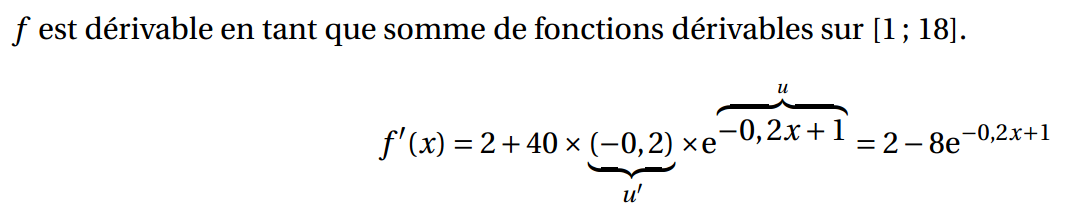
c. Expliquer comment retrouver la réponse obtenue dans la question 1. a.

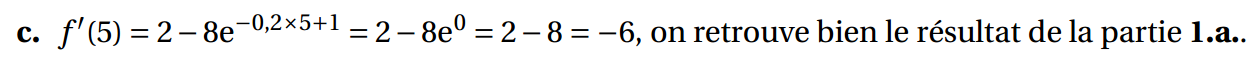
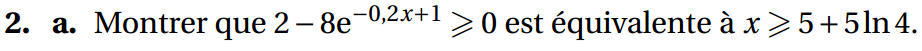
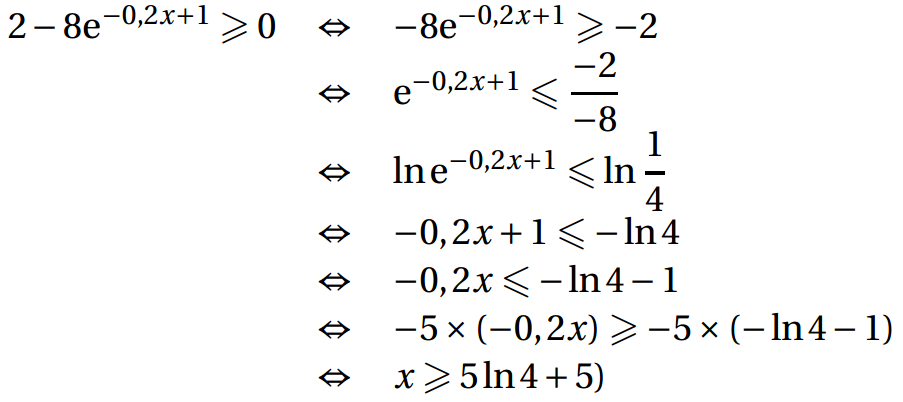
b. En déduire le signe de f′(x) et le tableau de variations de f sur [1 ; 18]. Les valeurs seront arrondies au centime d’euro dans le tableau de variations.

3. Déterminer, par le calcul, le nombre de parasols que doit produire l’entreprise pour que le coût de fabrication unitaire soit minimal.

I = \displaystyle\int_{5}^{15}f(x)\text{d}x =\left[F(x)\right]_5^{15}=F(15)-F(5)
=15^2+5\times 15-200e^{-3+1}-\left(5^2+5\times 5-200e^{-1+1}\right)
=300-200e^{-2}-(-150)=450-200e^{-2}

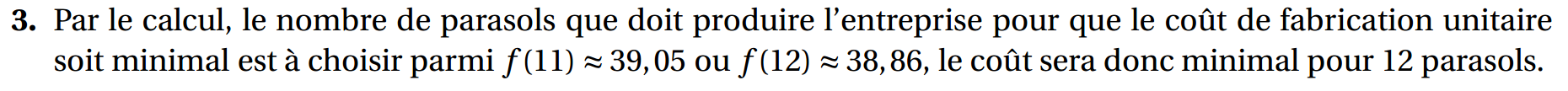
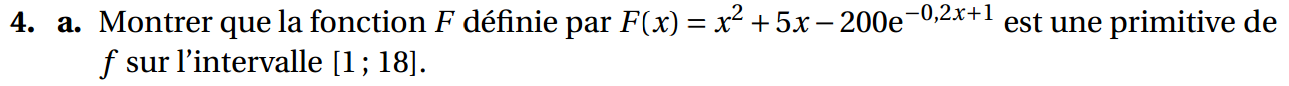
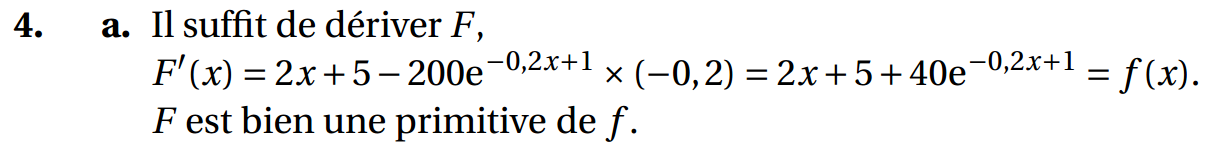
b.

C.

Rappel : la valeur moyenne de \(f\) sur \( \left[ a~;~b \right] \) vaut :

\mu= \dfrac{1}{b-a }~\displaystyle\int_{a}^{b}f(x)\text{d}x
\dfrac{1}{10}~I =\dfrac{1}{15-5}~\displaystyle\int_{5}^{15}f(x)\text{d}x

C'est la valeur moyenne de f sur l'intervalle [5 ; 15] et celle-ci vaut :

45-20e^{-2}\approx 42,29

C'est le coût de production unitaire moyen.

Amérique du sud 2015

Ex 1 : Proba.

Les probabilités demandées seront données à 0,001 près. Une étude est menée par une association de lutte contre la violence routière. Des observateurs, sur un boulevard d’une grande ville, se sont intéressés au comportement des conducteurs d’automobile au moment de franchir un feu tricolore.

Partie A

Dans cette partie, on s’intéresse au respect de la signalisation par les automobilistes. Sur un cycle de deux minutes (120 secondes), le feu est à la couleur « rouge » pendant 42 secondes, « orange » pendant 6 secondes et « vert » pendant 72 secondes. Par ailleurs, les observateurs notent que les comportements diffèrent selon la couleur du feu : 

  • lorsque le feu est rouge, 10 % des conducteurs continuent de rouler et les autres s’arrêtent ;
  • lorsque le feu est orange, 86 % des conducteurs continuent de rouler et les autres s’arrêtent ;
  • lorsque le feu est vert, tous les conducteurs continuent de rouler.

On s’intéresse à un conducteur pris au hasard, et on observe son comportement selon la couleur du feu. On note :

  • R l’évènement « le feu est au rouge » ;
  • O l’évènement « le feu est à l’orange » ;
  • V l’évènement « le feu est au vert » ;
  • C l’évènement « le conducteur continue de rouler ».

1. Modéliser cette situation par un arbre pondéré.

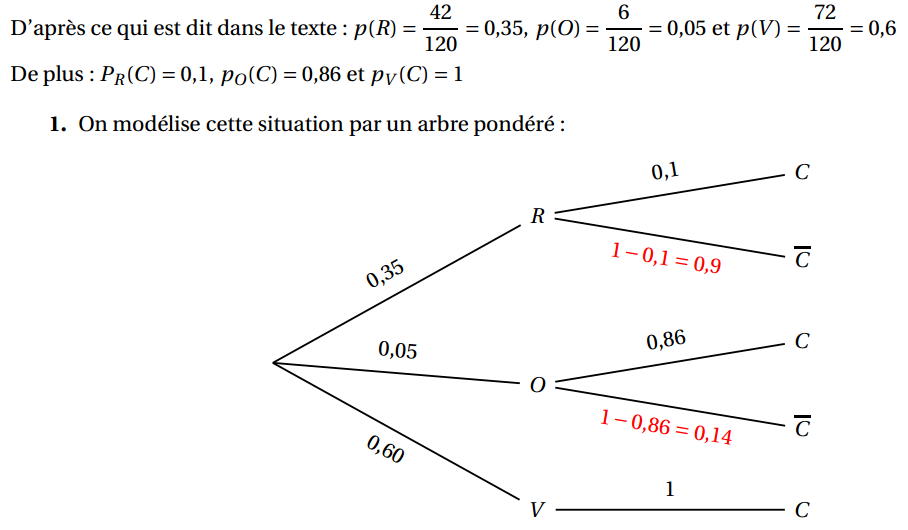
2. Montrer que la probabilité que le conducteur continue de rouler au feu est 0,678.

3. Sachant qu’un conducteur continue de rouler au feu, quelle est la probabilité que le feu soit vert ?

Ex 2 : Fonctions - Partie A

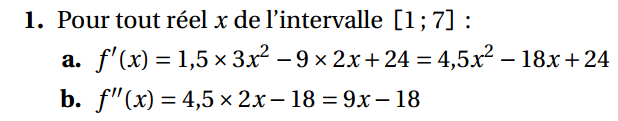
Partie B

Une entreprise fabrique et commercialise un article dont la production est comprise entre 1 000 et 7 000 articles par semaine. On modélise le coût de fabrication, exprimé en milliers d’euros, par la fonction f définie dans la partie A où \(x\) désigne le nombre de milliers d’articles fabriqués. On note \(c\) la fonction définie sur [1 ; 7] représentant le coût moyen par article fabriqué, exprimé en euros. On a, par conséquent, pour tout x de [1 ; 7] :

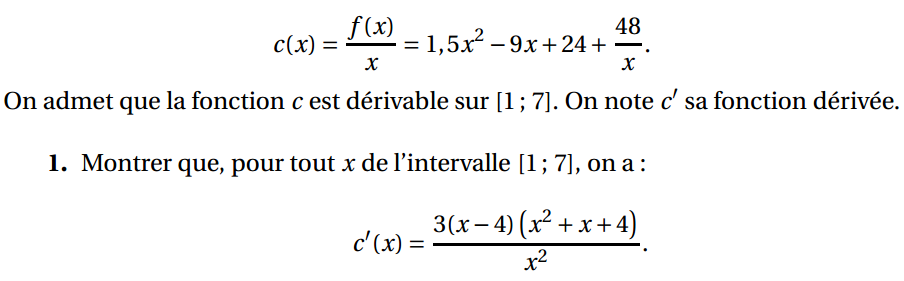
2. a. Étudier les variations de la fonction c sur l’intervalle [1 ; 7].

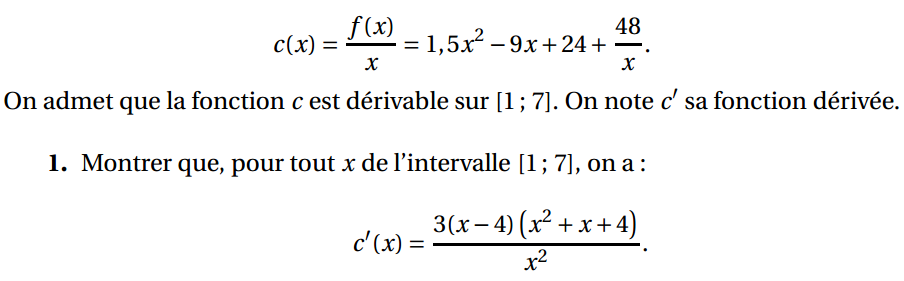
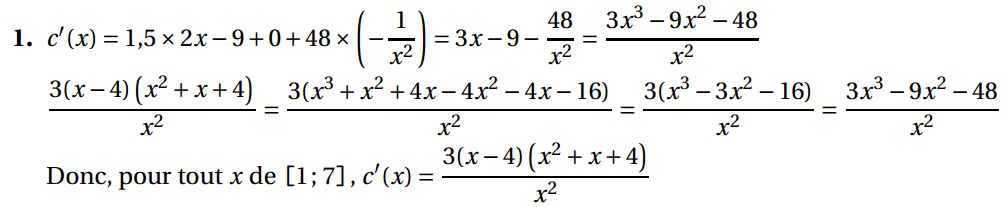
b. Déterminer, en milliers, le nombre d’articles à fabriquer pour que le coût moyen par article soit minimal.

Le minimum de la fonction c est atteint pour x = 4 donc pour 4000 articles à fabriquer ; le coût moyen par article est alors de 24×1000 soit 24000 euros.

Ex 3 : Suites 

Claudine est une passionnée de lecture abonnée à l’hebdomadaire littéraire « La Lecture ». Elle se rend une fois par semaine à la bibliothèque et elle demande ou non l’avis du bibliothécaire sur le livre mis en valeur dans l’hebdomadaire « La Lecture ». Son souhait de demander un avis change d’une semaine sur l’autre selon le plaisir qu’elle a eu à lire le livre et selon la pertinence du conseil donné par le bibliothécaire la semaine précédente. La première semaine, on suppose que la probabilité que Claudine demande un avis vaut 0,1.

Pour tout nombre entier naturel n strictement positif, on note an la probabilité que Claudine demande un avis la n-ième semaine. On a ainsi a1 = 0,1. On admet que, pour tout nombre entier naturel n strictement positif, on a : an+1 = 0,5an +0,4.

1. Calculer la probabilité a2 que Claudine demande un avis la deuxième semaine.

a2 = 0,5a1 +0,4 = 0,5 × 0,1+ 0,4 = 0,45. La probabilité que Claudine demande un avis la deuxième semaine est égale à 0,45.

2. Pour tout nombre entier naturel n strictement positif, on définit la suite (vn) par : vn = an −0,8.

a. Montrer que la suite (vn) est une suite géométrique de raison 0,5. Préciser son premier terme v1.

v_{n+1} = a_{n+1} - 0,8
v_{n+1} = 0,5a_n+0,4 - 0,8
v_{n+1} = 0,5a_n-0,4
v_{n+1} = 0,5(a_n-\frac{0,4}{0,5})
v_{n+1} = 0,5(a_n-0,8)
v_{n+1} = 0,5v_n
Pour \; n\geq1

La suite (vn) est donc bien une suite géométrique de raison q = 0,5.

v_1 = a_1- 0,8=0,1-0,8=-0,7

Son premier terme est v1 = −0,7.

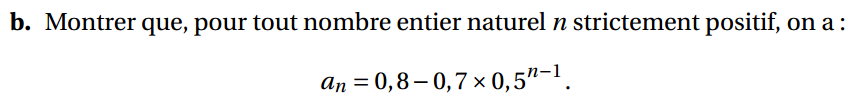
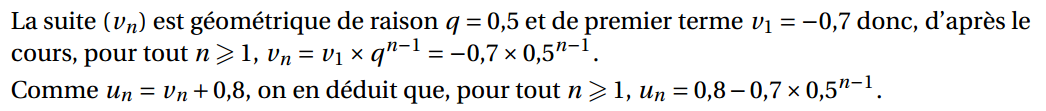
La suite (vn) est géométrique de raison q = 0,5 ; or 0 < 0,5 < 1 donc la suite (vn) est convergente et a pour limite 0.

c. Déterminer la limite de la suite (vn).

d. En déduire la limite de la suite (an). Interpréter ce résultat.

b. En déduire l’affichage de N obtenu en sortie d’algorithme quand la valeur de L est 0,7.

L’affichage de N obtenu en sortie d’algorithme quand la valeur de L est 0,7 est donc 4.

c. Dans le contexte de cet exercice, expliquer comment on peut interpréter le nombre N obtenu en sortie de l’algorithme quand le nombre L est compris strictement entre 0,1 et 0,8.

Le nombre N obtenu par l’algorithme quand le nombre L est compris entre 0,1 et 0,8 est le nombre de semaines à partir duquel la probabilité que Claudine demande un avis est supérieur à L.

4. Déterminer le nombre de semaines à partir duquel la probabilité que Claudine demande un avis soit supérieure à 0,799.

2 méthodes :

  1. Utiliser le mode suite de la calculatrice

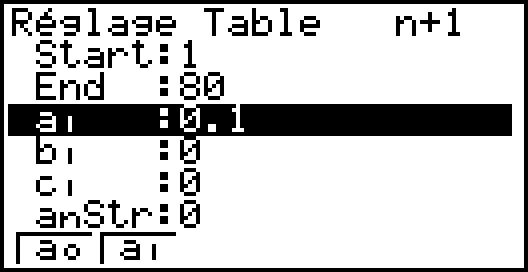
n = 11 . Le nombre de semaines à partir duquel la probabilité que Claudine demande un avis est supérieure à 0,799 est 11.

2. Utiliser le programme seuil

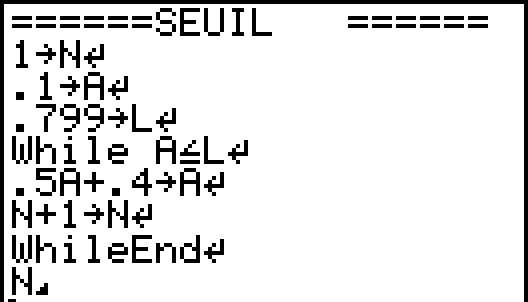
Métropole septembre 2017

Dans cet exercice, on étudie le tirage moyen journalier des quotidiens français d’information générale et politique, c’est-à-dire le nombre moyen d’exemplaires imprimés par jour. Le tableau suivant donne, entre 2007 et 2014, pour chaque année ce tirage moyen journalier, en milliers d’exemplaires :

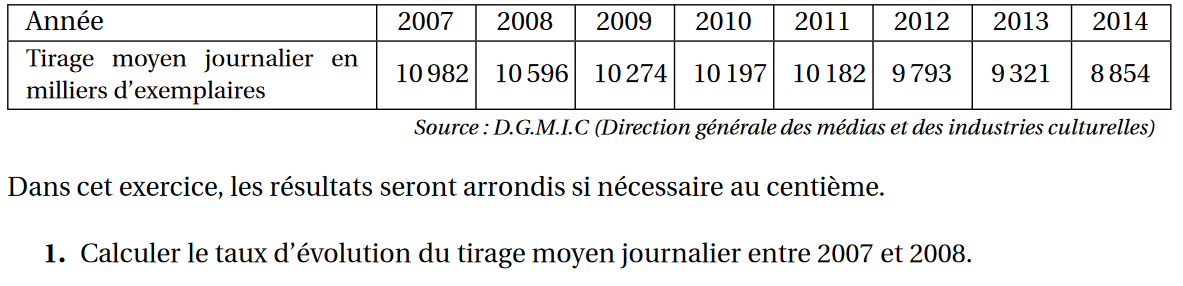
t = \frac{V_f-V_i}{V_i}= \frac{10596-10982}{10982}\approx -0,035

Le taux d'évolution est -0,035 soit -3,5%

-0,035\times 100=-3,5
V_1=0,96V_0+100=0,96\times10982+100=10642,72
V_2=0,96V_1+100=0,96\times10642,72+100=10317,01
W_{n+1} = V_{n+1} - 2500
W_{n+1} = 0,96V_n+100 - 2500
W_{n+1} = 0,96V_n-2400
W_{n+1} = 0,96(V_n-\frac{2400}{0,96})
W_{n+1} = 0,96(V_n-2500)
W_{n+1} = 0,96W_n
Pour\; tout\; n\in\mathbb{N}\;:

On a montré que la suite (Wn) est géométrique de raison 0,96.

Son\; premier\; terme \;est\;W_0=V_0-2500 = 10982−2500=8482.
Wn=8482\times 0,96^n
Wn=V_n-2500\Leftrightarrow V_n = W_n+2500
\Leftrightarrow V_n =8482\times 0,96^n +2500

a. Le tirage moyen journalier prévu pour l'année 2017 correspond à V10 :

V_{10} = 8482\times 0,96^{10} +2500=8139,11

Soit 8139,11 milliers d'exemplaires.

\textbf{b.} 0,96<1 \;donc\; (W_n)\; converge\; vers\;0
et\;(V_n)\;converge\;vers\;2500.

Année après année, le tirage moyen journalier va se rapprocher de 2500 milliers d'exemplaires.

Proposer un algorithme affichant le tirage moyen journalier, à partir de 2007 jusqu’à l’année (2007+n), pour un nombre d’années n saisi par l’utilisateur.

Pour i variant de 0 à n

   

afficher \;8482\times 0,96^i +2500

fin pour

algo 1 : avec la formule explicite

Pour i variant de 1 à n

afficher\; V

fin pour

algo 2 : avec la relation de récurrence

V               10982

Ici ce n'est pas un problème de seuil  avec une boucle non bornée tant que (while) mais des calculs de termes avec une boucle bornée pour (for).

afficher V

V              0,96V +100

V prend la valeur 10982

V           10982

Notation depuis l'an 2018 :

Polynésie 2019

Ex 3 : Suites

\dfrac{60}{150}=0,4

donc par 150 les capsules coûtent 0,40 € l'unité.

La réduction est donc de 0,20 sur 0,60 soit un tiers donc environ 33,33 %.

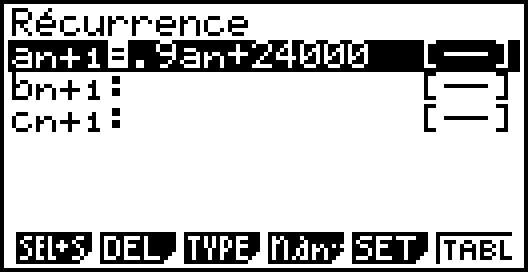
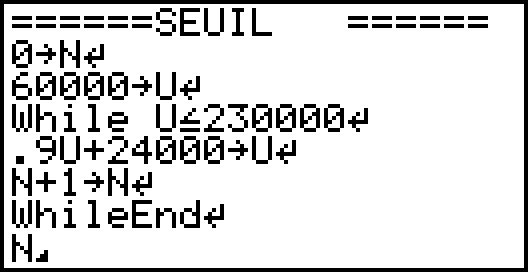
Au 1er janvier 2017, on comptait 60 000 utilisateurs de cette machine à café donc u0 = 60 000.

Retirer 10%  c’est multiplier par 0,9. On passe du mois n au mois n+1 en multipliant par 0,9 puis en ajoutant 24 000. On peut donc dire que pour tout entier n :

u_{n+1} = 0,9u_n + 24 000
v_{n+1} = u_{n+1} - 240000
v_{n+1} = 0,9u_n+24000- 240000
v_{n+1} = 0,9u_n-216000
v_{n+1} = 0,9(u_n-\frac{216000}{0,9})
v_{n+1} = 0,9(u_n-240000)
v_{n+1} = 0,9v_n
Pour\; tout\; n\in\mathbb{N}\;:

On a montré que la suite (vn) est géométrique de raison 0,9.

Son\; premier\; terme \;est\;v_0=u_0-240000 = 60000-240000=-180000.
a.\;v_n=-180000\times 0,9^n
b.\;v_n=u_n-24000\;donc\; u_n =240000+v_n=240000-180000\times 0,9^n

méthode 1 : Utiliser le mode suite de la calculatrice

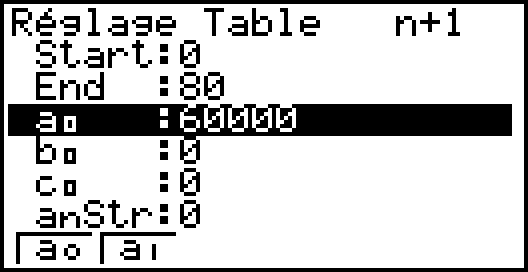
Le nombre d’utilisateurs dépassera la première fois 230 000 le 28e mois.

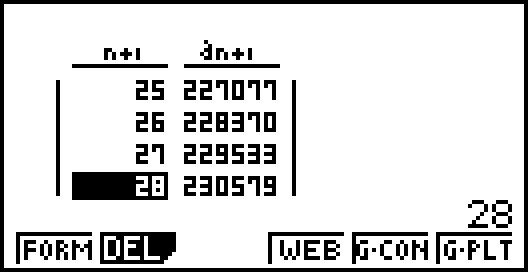
méthode 2 : Utiliser le programme seuil

On détermine la limite de (un) :

u_n=240000-180000\times 0,9^n
0,9<1 \;donc\; (v_n)\; converge\; vers\;0.
On\;en\;déduit\;que\;(u_n)\;converge\;vers\;240000.

D'après ce modèle l'entreprise ne touchera jamais plus de 240 000 utilisateurs donc on peut penser que cette affirmation est fausse.

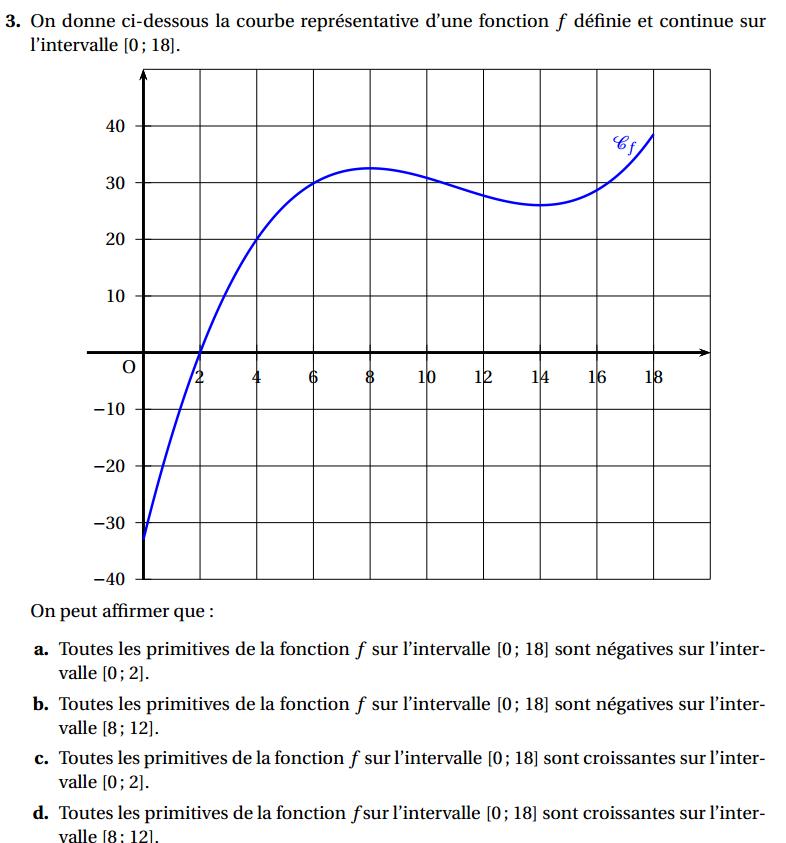
Ex 4 : QCM 

Pour la fête du village de Boisjoli, le maire a invité les enfants des villages voisins. Les services de la mairie ayant géré les inscriptions dénombrent 400 enfants à cette fête ; ils indiquent aussi que 32 % des enfants présents sont des enfants qui habitent le village de Boisjoli.

1. Le nombre d’enfants issus des villages voisins est :

a. 128     b. 272     c. 303     d. 368

Lors de cette fête, huit enfants sont choisis au hasard afin de former une équipe qui participera à un défi sportif. On admet que le nombre d’enfants est suffisamment grand pour que cette situation puisse être assimilée à un tirage au hasard avec remise. On appelle X la variable aléatoire prenant pour valeurs le nombre d’enfants de l’équipe habitant le village de Boisjoli.

Amérique du sud 2015

2. La variable aléatoire X suit la loi binomiale de paramètres :

a. n = 400 et p = 0,32         b. n = 8 et p = 0,32

c. n = 400 et p = 8               d. n = 8 et p = 0,68

3. La probabilité que dans l’équipe il y ait au moins un enfant habitant le village de Boisjoli est :

a. 0,125     b. 0,875     c. 0,954     d. 1

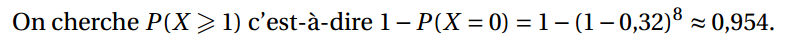
4. L’espérance mathématique de X est :

a. 1,740 8     b. 2,56     c. 87,04     d. 128

Made with Slides.com