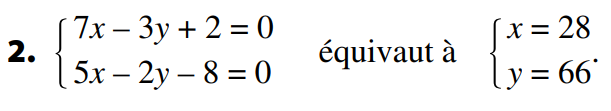1S : Vecteurs - colinéarité

Vecteurs - Colinéarité

donc le quadrilatère BDCA est un parallélogramme.

\vec{BD}=\vec{AC}

On en déduit que

\vec{BA}=\vec{DC}.

Il en résulte que

\vec{AE}=\vec{DC}

et le quadrilatère ADCE est un parallélogramme.

Vecteurs - Colinéarité

1 Colinéarité de deux vecteurs

1.1 Vecteurs colinéaires

Remarque : On conviendra que le vecteur nul est colinéaire à tous les vecteurs.

\vec{0}

Applications :

Deux droites (AB) et (CD) sont parallèles si et seulement si les vecteurs sont colinéaires.
Trois points A, B et C sont alignés si et seulement si les vecteurs sont colinéaires.

\vec{AB}\;et\;\vec{CD}

\vec{AB}\;et\;\vec{AC}

1.2 Expression de la colinéarité dans un repère

Remarque :

Cette propriété est due au fait que deux vecteurs sont colinéaires si et seulement si leurs coordonnées sont proportionnelles.

2 Décomposition d’un vecteur

2.1 Décomposer un vecteur suivant deux vecteurs non colinéaires

Exemples :

1) Sur la figure ci-dessous on a :

\vec{w}=3\vec{u}+2\vec{v}

Théorème 2 : (admis) Soit A, B et C trois points du plan non alignés. Alors, pour tout point M du plan, il existe un unique couple de réels (x ; y) tel que :

\vec{AM}=x\vec{AB}+y\vec{AC}

Remarques :

Cette décomposition est souvent obtenue grâce à la relation de Chasles.
On utilise souvent ce type de décomposition pour des problèmes de colinéarité (voir exercice résolu B page 172 TransMath 2011)

2.2 Une nouvelle notation pour les repères

Soit O, I, J trois points non alignés. Ils forment donc le repère (O ; I ; J).

Les vecteurs ne sont pas colinéaires, donc d’après le 2.1, pour tout point M du plan, il existe un unique couple (x ; y) tel que : Ce couple (x ; y) est en fait le couple de coordonnées du point M dans le repère (O ; I ; J)

On notera donc ce repère sous la forme :

\vec{OM}=x\vec{i}+y\vec{j}

\vec{i}\;et\;\vec{j}

(O;\vec{i};\vec{j})

Remarque : Le choix d’un point et de deux vecteurs non colinéaires permet donc de définir un repère du plan. Choisir un repère peut permettre de résoudre plus facilement des problèmes liés à la colinéarité (voir exercice résolu F page 176 TransMath).

5\vec{AD}=3\vec{AB}+2\vec{AC}\Leftrightarrow 5(\vec{AB}+\vec{BD})=3\vec{AB}+2\vec{AC}

\Leftrightarrow 5\vec{AB}+5\vec{BD}=3\vec{AB}+2\vec{AC}

\Leftrightarrow 5\vec{BD}=-2\vec{AB}+2\vec{AC}

\Leftrightarrow \vec{BD}=\frac{2}{5}\vec{AC}-\frac{2}{5}\vec{AB}

\Leftrightarrow \vec{BD}=\frac{2}{5}(\vec{AC}-\vec{AB})

\Leftrightarrow \vec{BD}=\frac{2}{5}(\vec{AC}+\vec{BA})

\Leftrightarrow \vec{BD}=\frac{2}{5}\vec{BC}

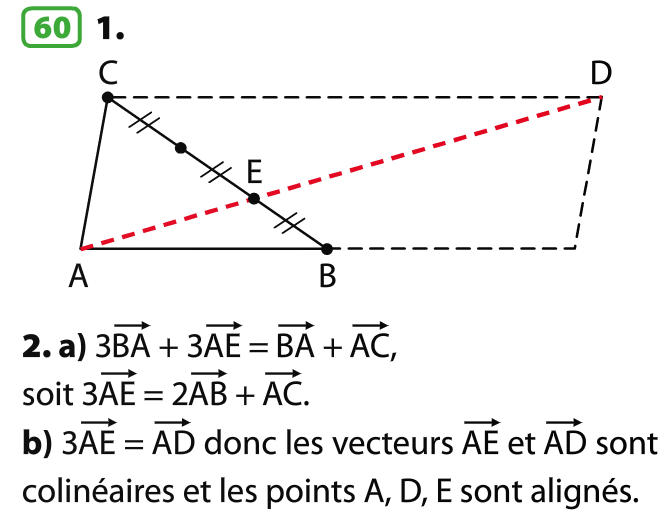
2 (a) (b)

Les vecteurs sont colinéaires donc les points B, C et D sont alignés.

\vec{BD}\;et\;\vec{BC}

\vec{IJ}=\vec{IA}+\vec{AJ}

2 (a)

=\vec{AJ}-\vec{AI}

=2\vec{AB}+\vec{AC}-\vec{AB}-2\vec{AC}

=\vec{AB}-\vec{AC}

\vec{IJ}=\vec{CA}+\vec{AB}

donc les droites (IJ) et (BC) sont parallèles.

\vec{IJ}=\vec{CB}

2 (b)

\vec{AG}=\vec{AF}+\vec{AE}

AEGF est un parallélogramme donc

\vec{AG}=3\vec{AD}+\vec{AB}+\vec{BE}

\vec{AG}=3\vec{AD}+3\vec{AB}

\vec{AG}=3(\vec{AD}+\vec{AB})

\vec{AG}=3\vec{AC}

(ABCD, parallélogramme)

Les vecteurs

sont colinéaires donc

les points A, C et G sont alignés.

\vec{AG} \;et\;\vec{AC}

\vec{u}=\frac{3}{2}\vec{i}+2\vec{j}

\vec{v}=\vec{i}-3\vec{j}

\vec{w}=-\frac{3}{2}\vec{i}-4\vec{j}

\vec{AD}=3\vec{AB}-2\vec{AC}\Leftrightarrow \vec{AB}+\vec{BD}=3\vec{AB}-2\vec{AC}

\Leftrightarrow \vec{BD}=2\vec{AB}-2\vec{AC}

2 (a)

2 (b)

\vec{BD}=2\vec{AB}-2\vec{AC}\Leftrightarrow \vec{BD}=2\vec{CA}+2\vec{AB}

\Leftrightarrow \vec{BD}=2(\vec{CA}+\vec{AB})

\Leftrightarrow \vec{BD}=2\vec{CB}

\Leftrightarrow \vec{BD}=-2\vec{BC}

Les vecteurs sont colinéaires donc les points B, C et D sont alignés.

\vec{BD}\;et\;\vec{BC}

\vec{IJ}=\vec{IB}+\vec{BA}+\vec{AJ}

=-\frac{1}{2}\vec{AB}-\vec{AB}+3\vec{AD}

\vec{IJ}=-\frac{3}{2}\vec{AB}+3\vec{AD}

2 (a)

\vec{IC}=\vec{IB}+\vec{BC}

=-\frac{1}{2}\vec{AB}+\vec{AD}

(ABCD est un parallélogramme donc )

\vec{BC}=\vec{AD}

2 (b)

\vec{IJ}=3\vec{IC}

\vec{IJ}\;et\;\vec{IC}

sont colinéaires

donc I, J et C sont alignés.

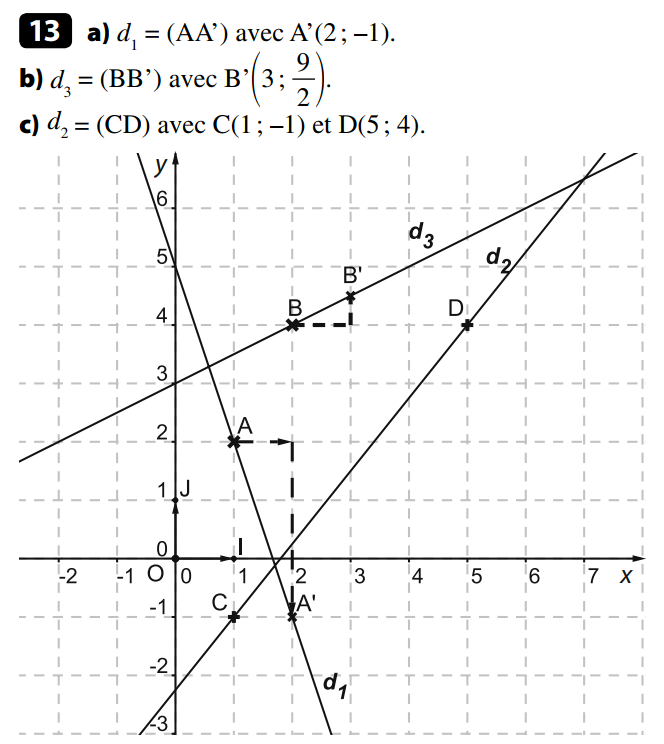
\vec{AE}=\dfrac{2}{3}\vec{AB}+\dfrac{1}{3}\vec{AC}

1.\;\vec{AP}=\vec{AB}-2\vec{AC}\Leftrightarrow \vec{AP}=\vec{AB}-2(\vec{AI}+\vec{IC})

\Leftrightarrow \vec{AP}=\vec{AB}-2\vec{AI}-2\vec{IC}

I est le milieu de [AB] donc

\vec{AB}=2\vec{AI}

On en déduit que

\vec{AP}=-2\vec{IC}

Les vecteurs sont donc colinéaires et les droites (AP) et (CI) sont parallèles.

\vec{AP}\;et\;\vec{IC}

\vec{AQ}=\frac{1}{3}\vec{CA}-\vec{CA}=\frac{2}{3}\vec{AC}

\vec{AR}=\vec{AC}+\vec{CR}

=-\frac{1}{3}\vec{AB}-\frac{4}{3}\vec{CA}

=\vec{CR}-\vec{CA}

=-\frac{1}{3}\vec{CA}-\frac{1}{3}\vec{AB}-\vec{CA}

=-\frac{1}{3}\vec{AB}+\frac{4}{3}\vec{AC}

\vec{CI}=\vec{CB}+\vec{BI}=-\vec{CK}+2\vec{CJ}

3 Équation cartésienne d’une droite

3.1 Vecteur directeur d’une droite

Définition : Soit d une droite.
On dit que le vecteur est un vecteur directeur de d si sa direction est celle de d .

\vec{u}

Remarques :

Tout vecteur non nul, colinéaire à est aussi un vecteur directeur de la droite d.
Si A et B sont deux points distincts de d, alors est un vecteur directeur de d.
La droite d est entièrement déterminée par la donnée d’un point A et d’un vecteur directeur

\vec{AB}

\vec{u}.

Propriété : Soit d et d' deux droites de vecteurs directeurs respectifs d et d' sont parallèles si et seulement si sont colinéaires.

\vec{u}\;et\;\vec{u'}.

\vec{u}\;et\;\vec{u'}

3.2 Équation cartésienne d’une droite

Théorème : Dans un repère :

Toute droite admet une équation de la forme ax + by + c = 0.
Réciproquement, toute équation de la forme ax + by + c = 0 (avec a et b non simultanément nuls) est une équation de droite. Cette équation est appelée équation cartésienne de la droite.

(O;\vec{i};\vec{j})

Remarque : Il n’y a pas unicité de l’équation cartésienne d’une droite. La droite D d’équation x − y + 1 = 0 admet aussi comme équation 2x − 2y + 2 = 0 ou −x + y − 1 = 0 par exemple.

D’après la démonstration précédente, on a la propriété suivante :

Propriété : Soit D la droite d’équation ax + by + c = 0.

Le vecteur est un vecteur directeur de D.

\vec {u}\begin{pmatrix} -b \\ a \end{pmatrix}

Exercice résolu : Trouver une équation cartésienne de la droite D passant par A (1 ; 2) et de vecteur directeur :

\vec {u}\begin{pmatrix} -1 \\ 3 \end{pmatrix}

\begin{pmatrix} -b \\ a \end{pmatrix} =\begin{pmatrix} -1 \\ 3 \end{pmatrix}donc \;a=3 \;et\;b=1

a) d est parallèle à \(\Delta\) donc d a une équation de la forme

\( 2x-y+c=0\) et \(A(0~;1) \in d\) donc \( 2\times 0-1+c=0\Leftrightarrow c=1\)

Une équation cartésienne de d : \( 2x-y+1=0\)

b) d est parallèle à \(\Delta\) donc d a une équation de la forme

\dfrac{4}{5}x-\dfrac{5}{7}y+c=0

A\left(\dfrac{7}{4}~;\dfrac{8}{5}\right) \in d\;donc

\dfrac{4}{5}\times \dfrac{7}{4}-\dfrac{5}{7}\times \dfrac{8}{5}+c=0\Leftrightarrow \dfrac{7}{5}-\dfrac{8}{7}+c=0\Leftrightarrow c=-\dfrac{9}{35}

\dfrac{4}{5}x-\dfrac{5}{7}y-\dfrac{9}{35}=0\Leftrightarrow 28x-25y-9=0

\( 28x-25y-9=0\) est une équation cartésienne de d.

3.3 Lien entre équation réduite et équation cartésienne

Propriété 1 : Soit D une droite d’équation cartésienne

ax + by + c = 0 (avec a et b non simultanément nuls).

Si b = 0, alors D est une droite parallèle à l’axe des ordonnées, qui admet une unique équation réduite de la forme x = k, avec k ∈ R.
Si b ≠ 0, alors la droite D n’est pas parallèle à l’axe des ordonnées ; elle admet une unique équation réduite de la forme y = mx + p avec m, p ∈ R.

Propriété 2 : Dans un repère

Toute droite parallèle à l’axe des ordonnées, qui admet une unique équation réduite de la forme x = k, avec k ∈ R, a comme vecteur directeur
Toute droite non parallèle à l’axe des ordonnées qui admet une unique équation réduite de la forme y = mx + p avec m, p ∈ R, a comme vecteur directeur

(O;\vec{i};\vec{j}) :

\vec {u}\begin{pmatrix} 0 \\ 1 \end{pmatrix}.

\vec {u}\begin{pmatrix} 1 \\ m \end{pmatrix}.

a=m \;et\;b=-1\;donc\begin{pmatrix} -b \\ a \end{pmatrix} =\begin{pmatrix} 1 \\ m \end{pmatrix}