La fonction exponentielle
Rappels sur le nombre dérivé

On considère une fonction \(f\), dérivable sur son ensemble de définition.
En tout point \(A(a~;~f(a))\) de la courbe représentative de \(f\), on peut tracer une tangente à la courbe.

Au voisinage du point A, la courbe et sa tangente sont quasiment confondues.
Le nombre dérivé \(f'(a)\) est le coefficient directeur de la tangente au point d'abscisse \(a\).

\(\vec{u}\left(\begin{array}{c}{1} \\ {f'(a)}\end{array}\right)\) est un vecteur directeur de la tangente.

Questions flash
30 s par question.
Question 1
La courbe \(C_𝑓\) représente une fonction 𝑓.
Donner \(𝑓(−4)\) et \(𝑓' (−4)\), \(𝑓(3)\) et \(𝑓' (3)\).

Question 2
Associer à chaque phrase une des égalités proposées
- La courbe \(𝐶_𝑓\) passe par le point (2 ; 3).
- Le coefficient directeur de la tangente en 3 est 2.
- Le vecteur \(\vec{u}\left(\begin{array}{c}{1} \\ {3}\end{array}\right)\) est un vecteur directeur de la tangente à \(𝐶_𝑓\) au point d’abscisse 2.
a. \(𝑓'(2)=3\)
b. \(𝑓'(3)=2\)
c. \(𝑓(3)=2\)
d. \(𝑓(2)=3\)
Question 3
Que peut-on dire d’une fonction définie sur ℝ telle que, pour tout réel \(a\), \(f(a)=2\) ?
Question 4
Quelles sont les fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=2\) ?
Correction
Question 1
\(𝑓(−4)=3\) ; \(𝑓' (-4)=−\frac{1}{2}\)

Question 1

\(𝑓(3)=-1\) et \(𝑓' (3)=2\).
Question 2
Associer à chaque phrase une des égalités proposées
- La courbe \(𝐶_𝑓\) passe par le point (2 ; 3).
- Le coefficient directeur de la tangente en 3 est 2.
- Le vecteur \(\vec{u}\left(\begin{array}{c}{1} \\ {3}\end{array}\right)\) est un vecteur directeur de la tangente à \(𝐶_𝑓\) au point d’abscisse 2.
a. \(𝑓'(2)=3\)
b. \(𝑓'(3)=2\)
c. \(𝑓(3)=2\)
d. \(𝑓(2)=3\)
Question 3
Que peut-on dire d’une fonction définie sur ℝ telle que, pour tout réel \(a\), \(f(a)=2\) ?

Une seule fonction convient, la fonction constante égale à 2.
Question 4

Quelles sont les fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=2\) ?
Question 4
Quelles sont les fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=2\) ?

Une infinité de fonctions conviennent :
Les fonctions affines de la forme \(f(x) = 2x+b\) où b est un réel.
Equations différentielles, première approche


Fonctions solutions d'une équation différentielle
Dans la question 4) nous nous sommes demandés : "Quelles sont les fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=2\) ?"
Une relation de ce type s'appelle une équation différentielle.
On peut la noter : \(y'=2\)
C'est une équation dans laquelle l'inconnue ne désigne pas un nombre mais une fonction.
Fonctions solutions d'une équation différentielle
1) Existe-t-il des fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=a\) ?
Pour tout réel \(a\), le coefficient directeur de la tangente au point d’abscisse \(a\) est \(a\).
Comment traduire cette contrainte graphiquement ?

Fonctions solutions d'une équation différentielle
Pour tout réel \(a\), \(f'(a)=a\). On obtient un champ de tangentes.

Fonctions solutions d'une équation différentielle

Pour tout réel \(a\), \(f'(a)=a\).
Une infinité de fonctions conviennent.
Fonctions solutions d'une équation différentielle
Pour tout réel \(a\), \(f'(a)=a\).
Si on ajoute une condition comme par exemple \(f(-1)=0\)
alors il existe une unique
solution au problème.

Fonctions solutions d'une équation différentielle
2) Existe-t-il des fonctions définies et dérivables sur ℝ telles que, pour tout réel \(a\), \(f'(a)=f(a)\) ?
On a \(f'(x)=0\) pour tout \(x\in\R\).
Donc pour tout réel \(a\), \(f'(a)=f(a)\).
La fonction constante égale à 0 est solution de l'équation différentielle \(y'=y\).
Existe-t-il d'autres fonctions telles que, pour tout réel \(a\), \(f'(a)=f(a)\) ?
Pour tout réel \(a\), le coefficient directeur de la tangente au point d’abscisse \(a\) est \(f(a)\).
Comment traduire cette contrainte graphiquement ?

Pour tout réel \(a\), \(f'(a)=f(a)\)
Fonctions solutions d'une équation différentielle
Pour tout réel \(a\), \(f'(a)=f(a)\). On obtient un autre champ de tangentes.

Fonctions solutions d'une équation différentielle
Pour tout réel \(a\), \(f'(a)=f(a)\).
Une infinité de fonctions conviennent.

Fonctions solutions d'une équation différentielle
Pour tout réel \(a\), \(f'(a)=f(a)\).
Si on ajoute une condition comme par exemple \(f(3)=4\)
alors il existe une unique
solution au problème.

Fonction exponentielle : fonction \(f\) définie et dérivable sur \(\R\) qui vérifie pour tout nombre réel \(x\) :
La fonction exponentielle
La fonction exponentielle est notée exp :
\(\exp(0) = 1\) et pour tout \(x\in\R\), \(\exp'(x) = \exp(x)\).
Démonstration partielle : Activités A et B p 158
\(f(0)=1\) et \(f'(x)=f(x)\)
N.B. elle est unique.
Construction de la courbe : méthode d'Euler
Construction de la courbe : méthode d'Euler


Équation de \(T_a\), la tangente à la courbe au point d'abscisse \(a\) :
Ordonnée du point de \(T_a\) d'abscisse \(a+h\) :
Au voisinage de \(a\), la courbe et la tangente sont très proches donc :
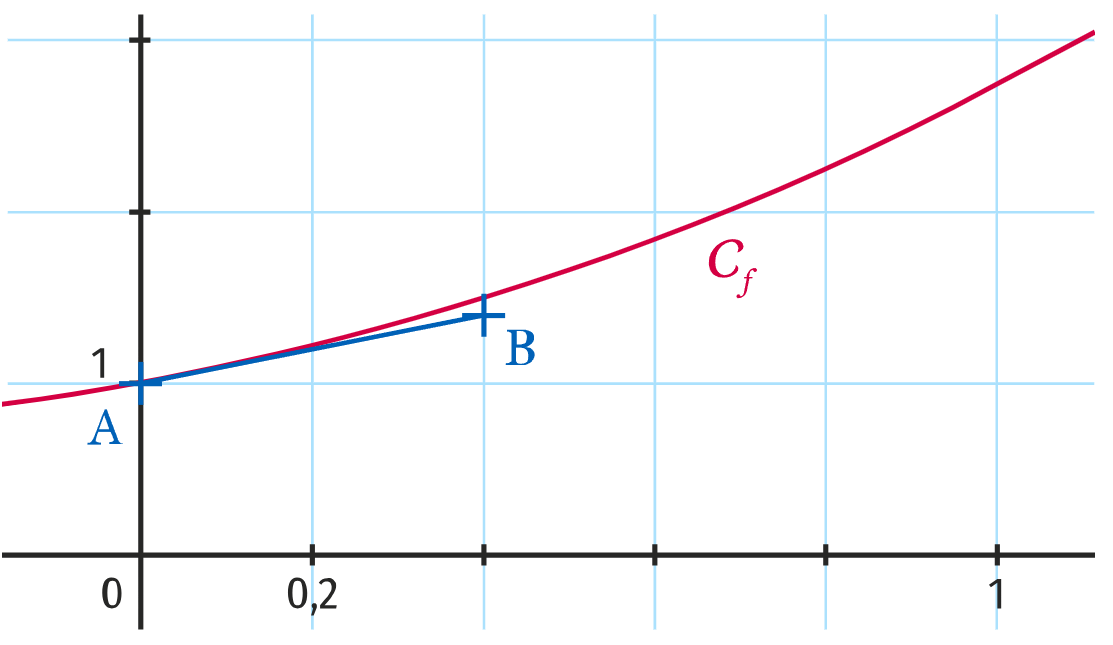




une approximation affine est une approximation d'une fonction au voisinage d'un point à l'aide d'une fonction affine.
approximation affine


On procède comme précédemment :
from matplotlib import pyplot as plt
n = 10
x = [] #liste des abscisses
y = [] #liste des ordonnées
x = x + [0]
y = y + [1]
for k in range(1, n + 1):
a = float(x[k - 1]) + 1/n
x = x + [a]
b = (1 + 1/n)*float(y[k - 1])
y = y + [b]
# Affichage des points dans le repère
plt.clf()
plt.plot(x, y, marker='o', linestyle='-')
plt.show()

Les lignes 9 à 13 servent à calculer les valeurs successives de la fonction :
- A la ligne 10 : calcul de l’abscisse suivante en ajoutant le pas à l'abscisse précédente.
- A la ligne 11 : ajout de cette abscisse à la liste des abscisses
- A la ligne 12 : calcul de l’ordonnée correspondante en multipliant l’ordonnée du point précédent par 1+ le pas
- A la ligne 13 : ajout de cette ordonnée à la liste des ordonnées.
import matplotlib.pyplot as plt
import numpy as np
from math import *
#Paramètres modifiables pour le tracé final.
#Prendre un pas négatif pour voir l'approximation pour les abscisses négatives.
pas=0.1
n=10
# Tracé de exp
x = np.linspace(0,1,100)
plt.plot(x,e**x,"c")
def expEuler(pas,n):
listeX = [i*pas for i in range(n+1)]
listeY = [(pas+1)**i for i in range(n+1)]
plt.plot(listeX,listeY,"o-")
expEuler(pas,n)Un autre script avec en plus l'affichage de la fonction exponentielle :




La fonction exponentielle est strictement positive sur \(\R\). Pour tout réel \(x\),
La fonction exponentielle est strictement croissante sur \(\R\).
Courbe représentative :
\(\exp(x)>0\).
Signe :
Variations :
Propriétés algébriques :
Pour tous réels \(x\) et \(y\) et pour tout entier relatif \(n\) :
- \(\exp (x+y)=\exp(x)\times \exp(y)\)
- \(\exp(-x)=\dfrac{1}{\exp(x)}\)
- \(\exp(x-y)=\dfrac{\exp(x)}{\exp(y)}\)
- \(\exp(nx)=(\exp(x))^n\)
Comme les puissances :
Nouvelle notation :
L'image de \(1\) par la fonction exponentielle est notée \(\text{e}\) (Nombre d'Euler).
\(\exp(1)=\text{e}\)
Avec la calculatrice on obtient :

Comme \(\pi\) ou \(\sqrt{2}\), c'est un nombre irrationnel.
On a vu que \(\exp(nx)=(\exp(x))^n\)
Pour \(x=1\), \(\exp(n)=\exp(n\times 1)=(\exp(1))^n=\text{e}^n\)
On généralise cette notation à tout réel \(x\) :
Nouvelle notation :
Propriétés algébriques avec la nouvelle notation :
Pour tous réels \(x\) et \(y\) et pour tout entier relatif \(n\) :
Les méthodes...


Simplifier des expressions :
Les méthodes...


Étudier des fonctions :


Maximum :



Les méthodes...
Étudier des fonctions :

Rappel : Équation de la tangente au point d'abscisse a :



Les méthodes...
Résoudre des équations ou des inéquations :

OK ou Paste

Avec la calculatrice, on obtient :

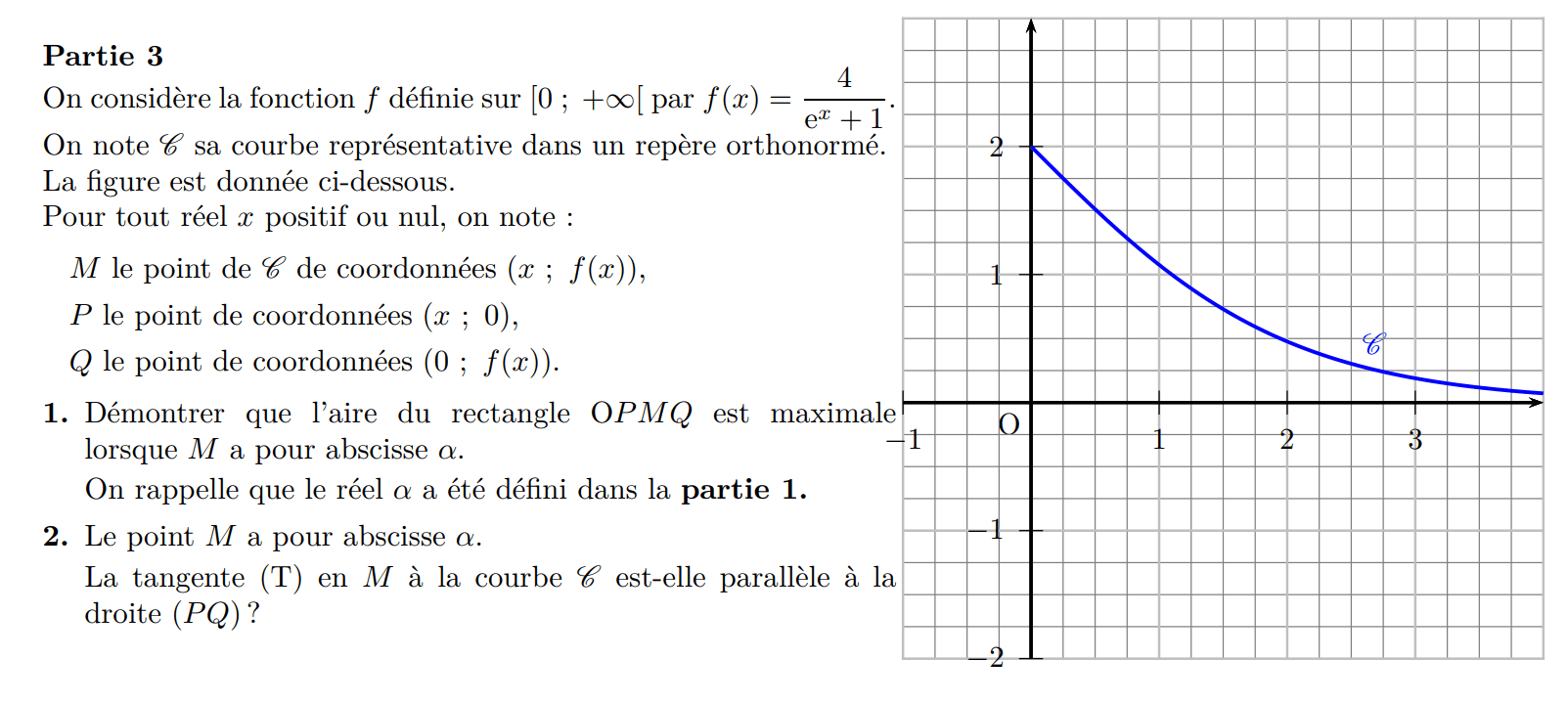
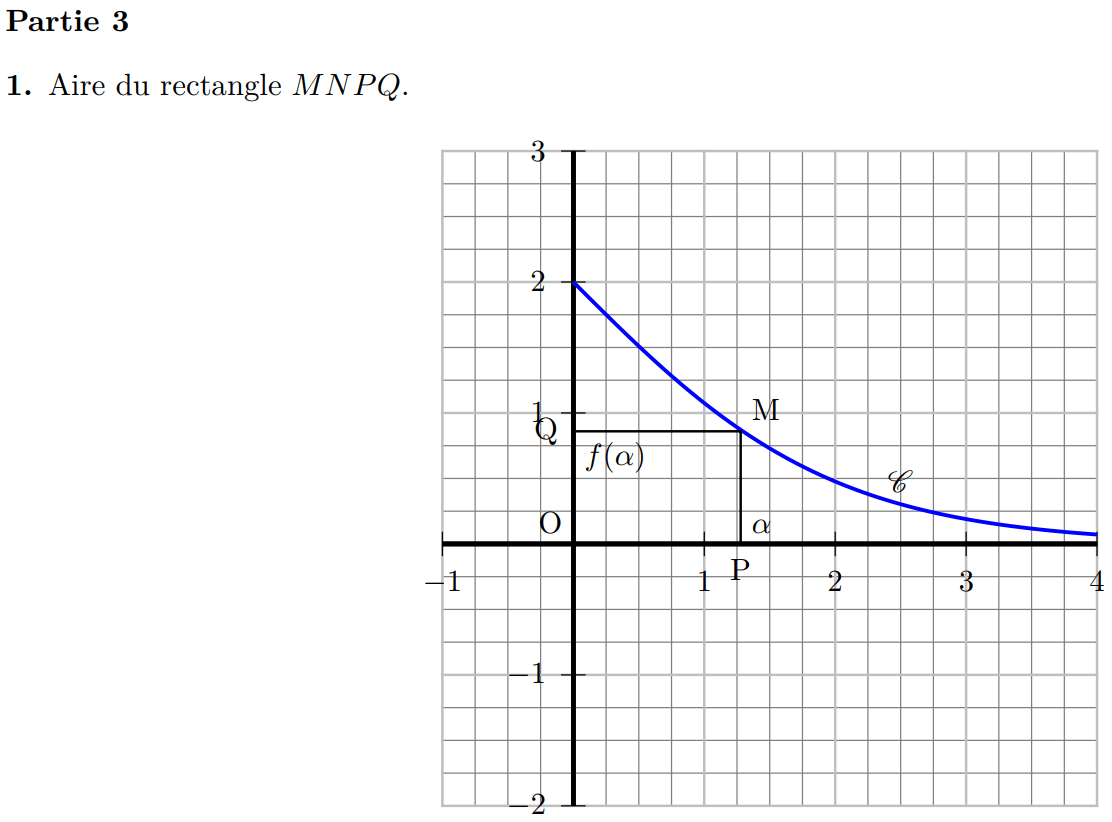
Ex 3 (fiche 2)







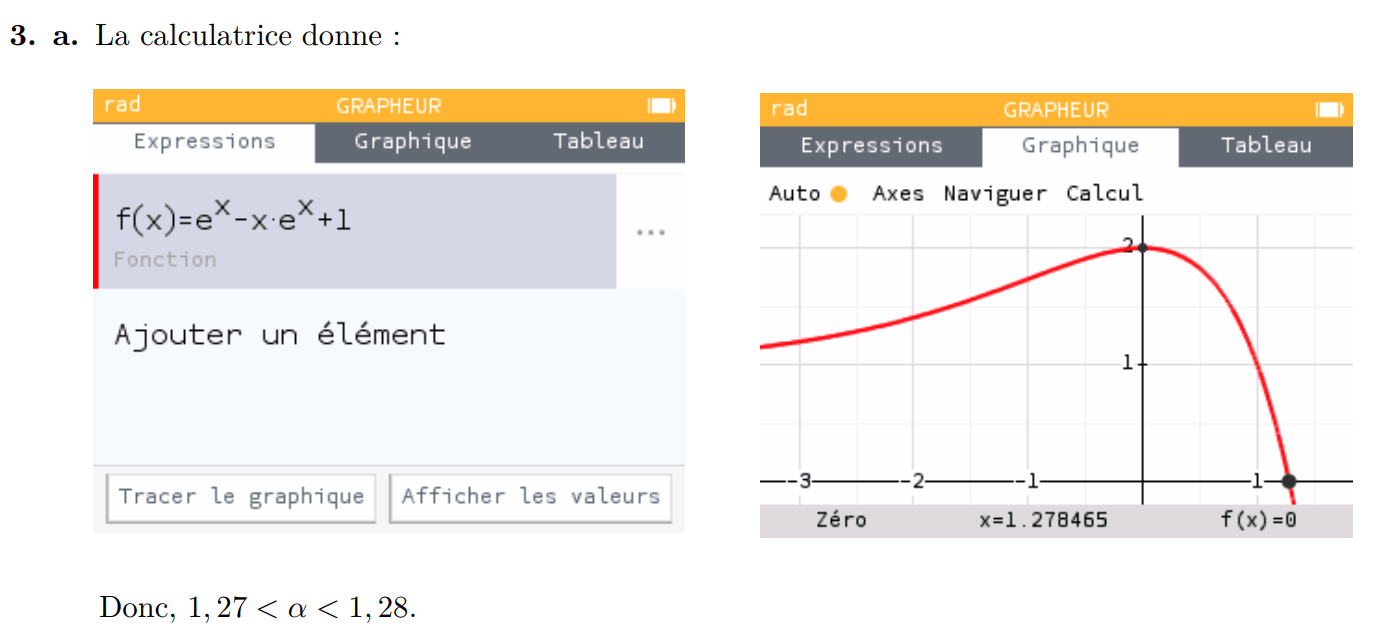

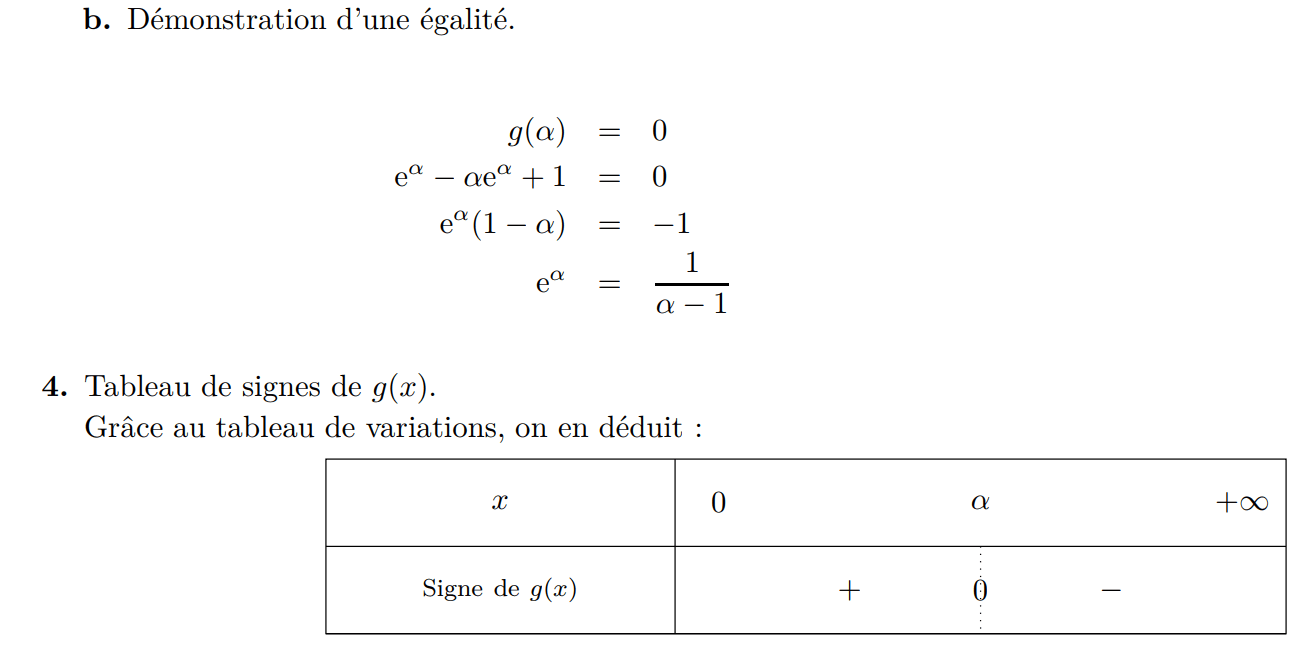
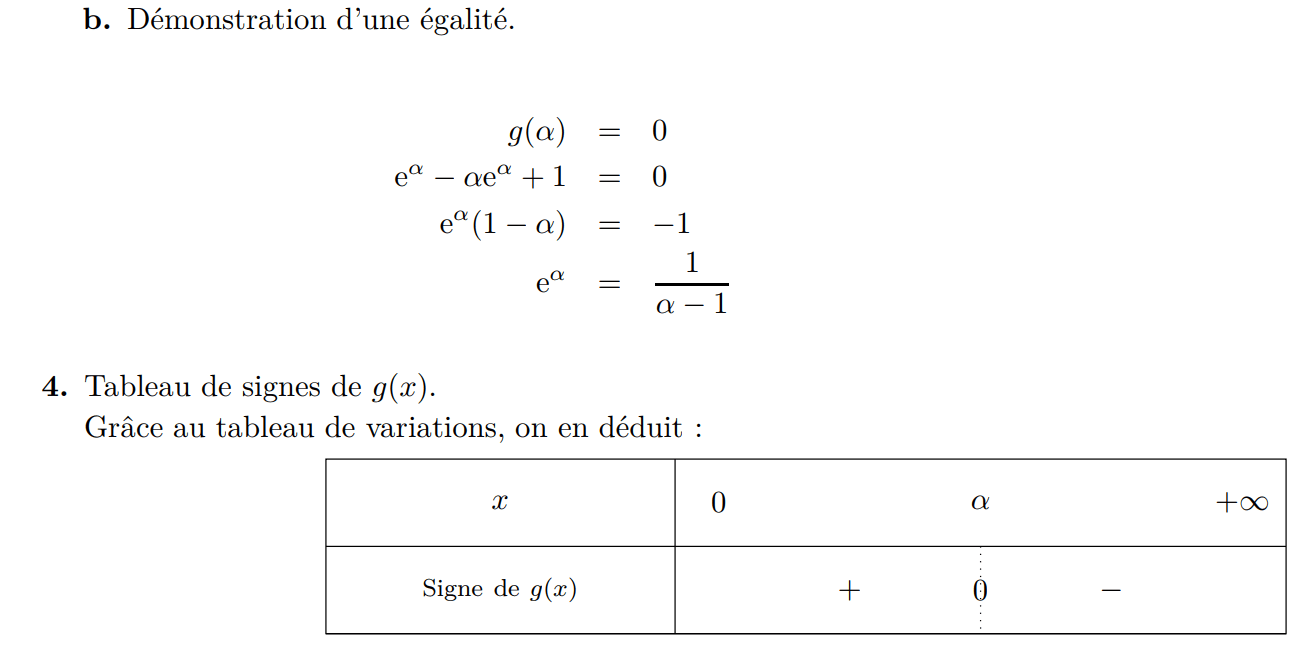
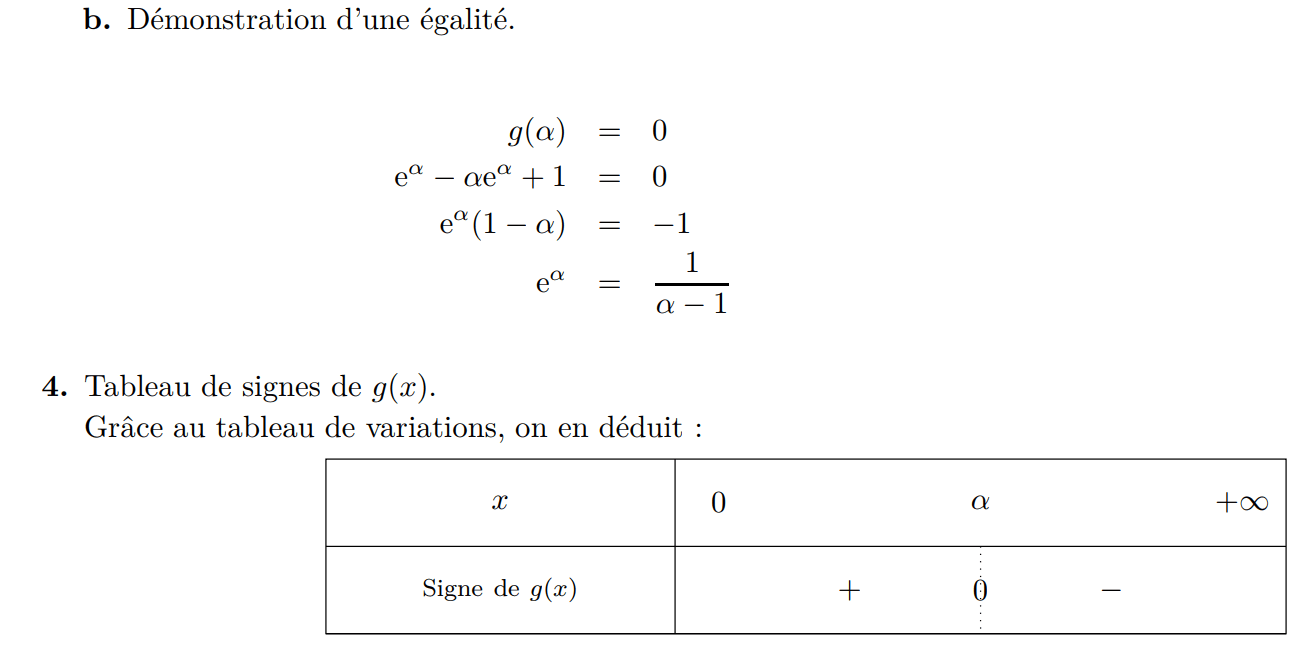
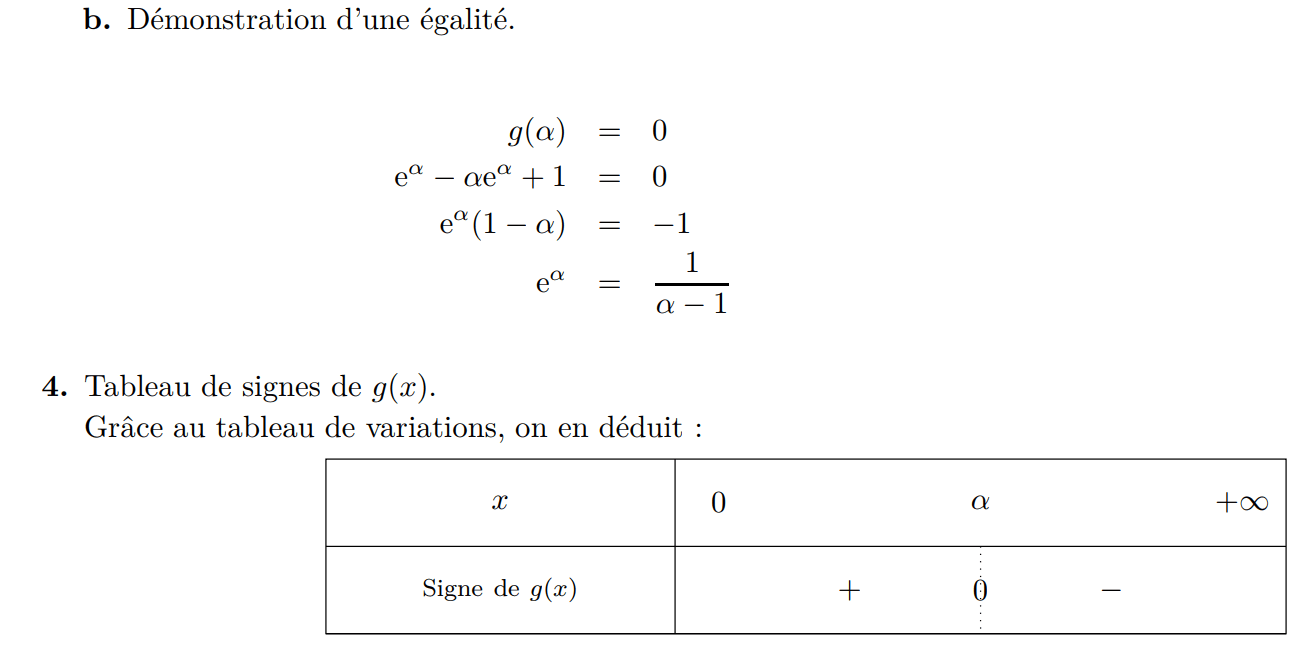

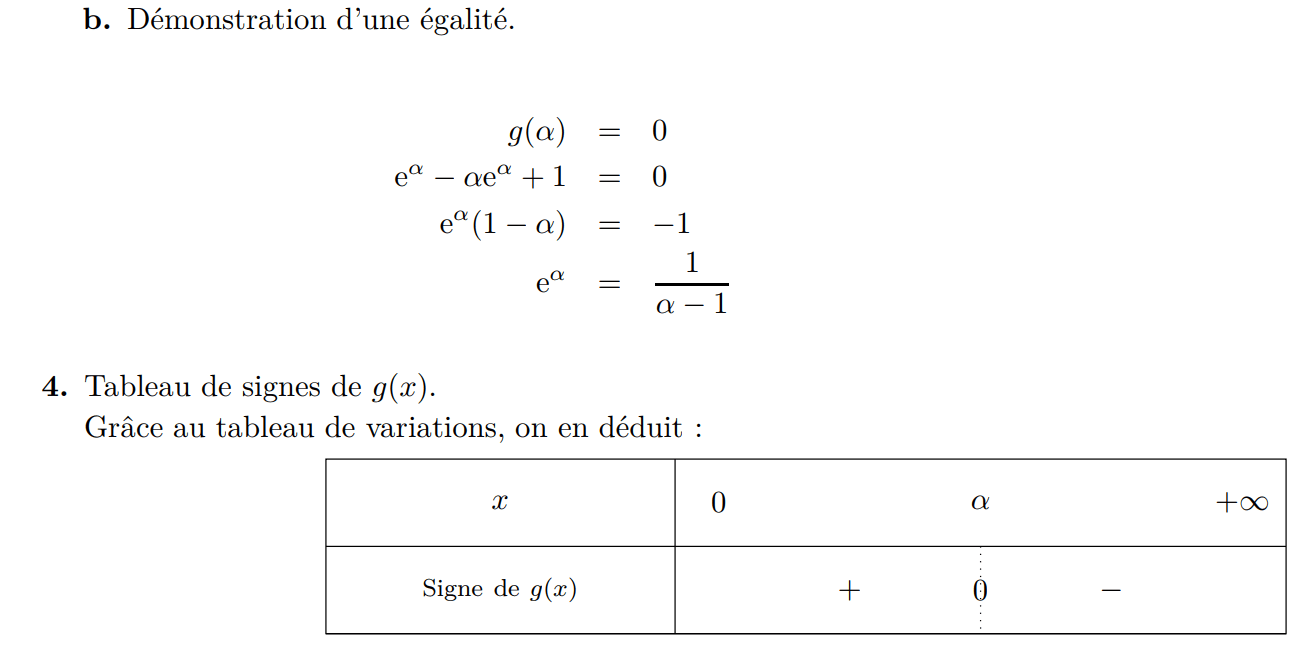









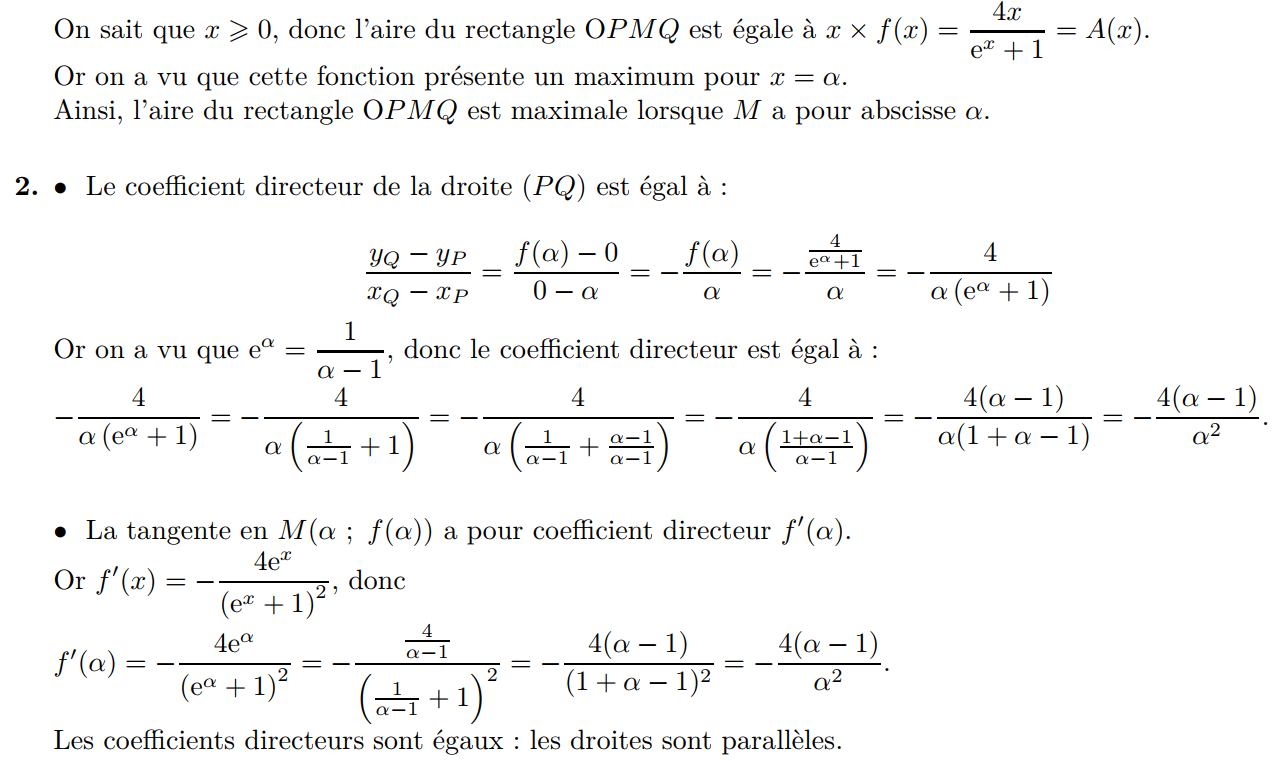

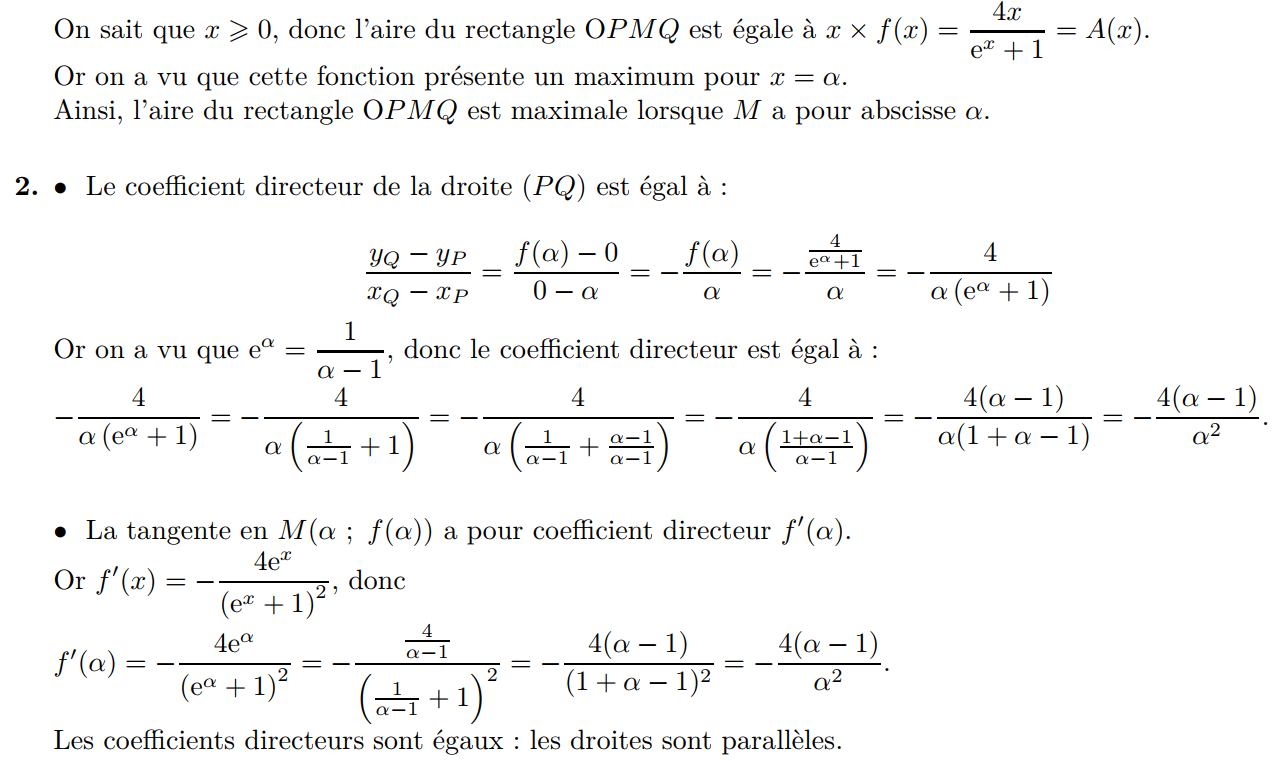

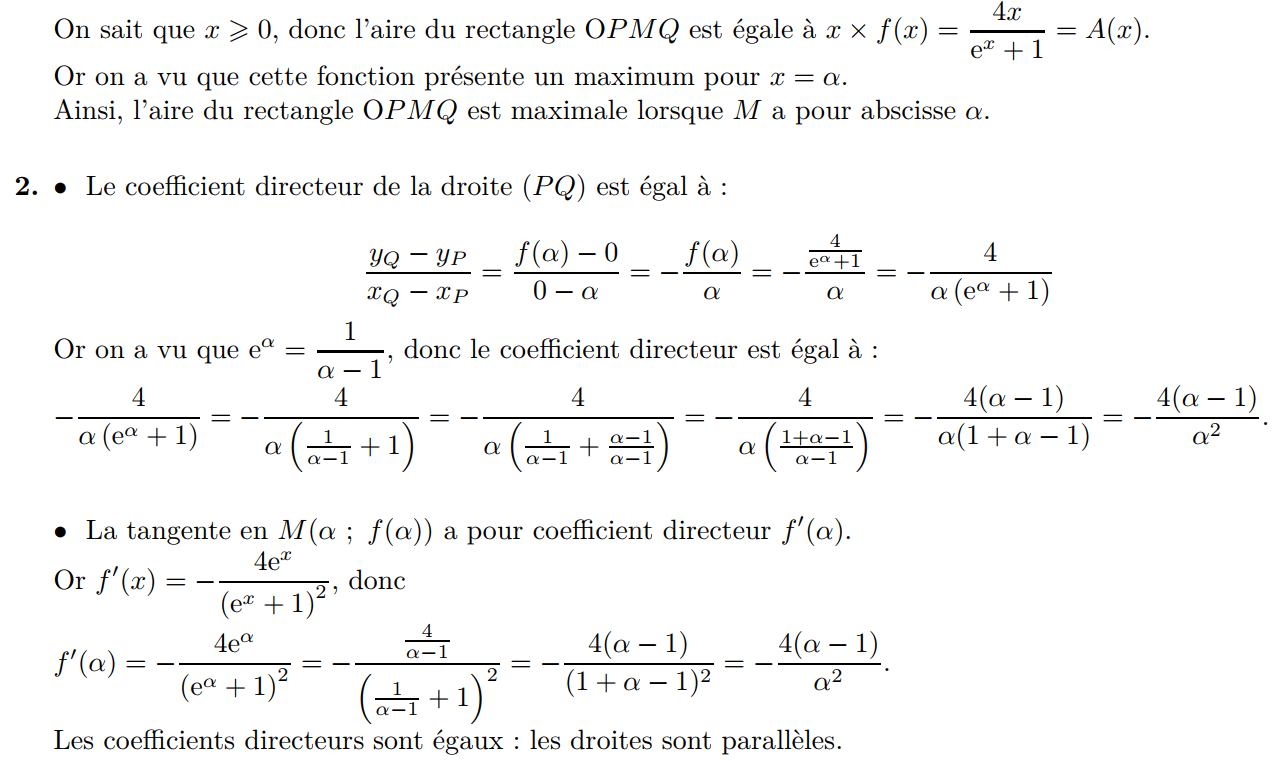
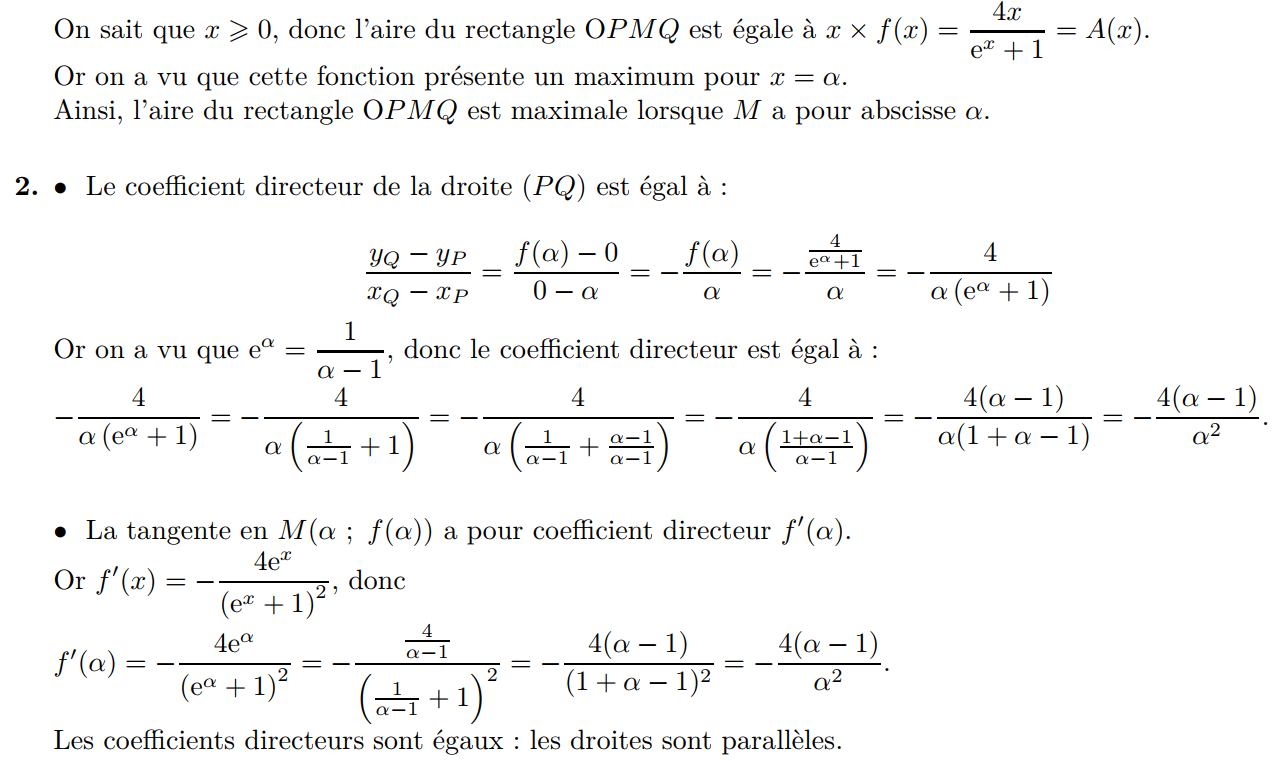
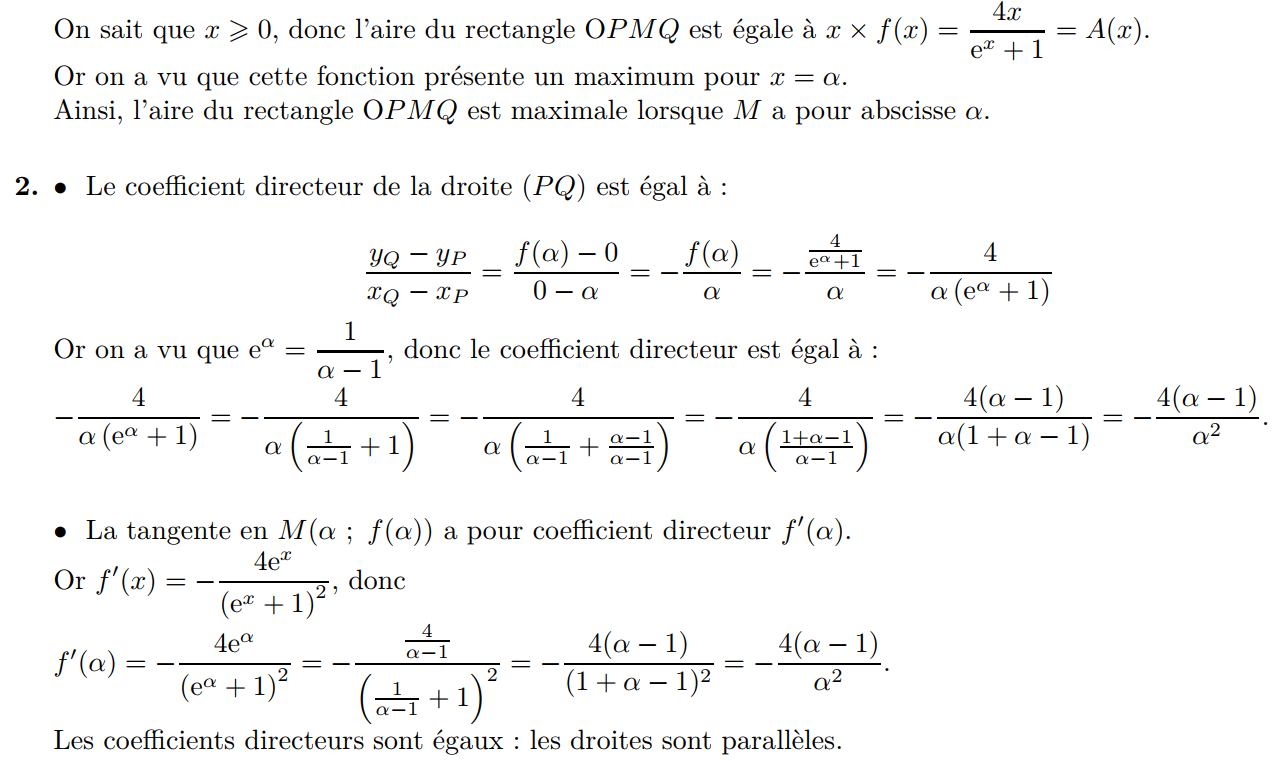
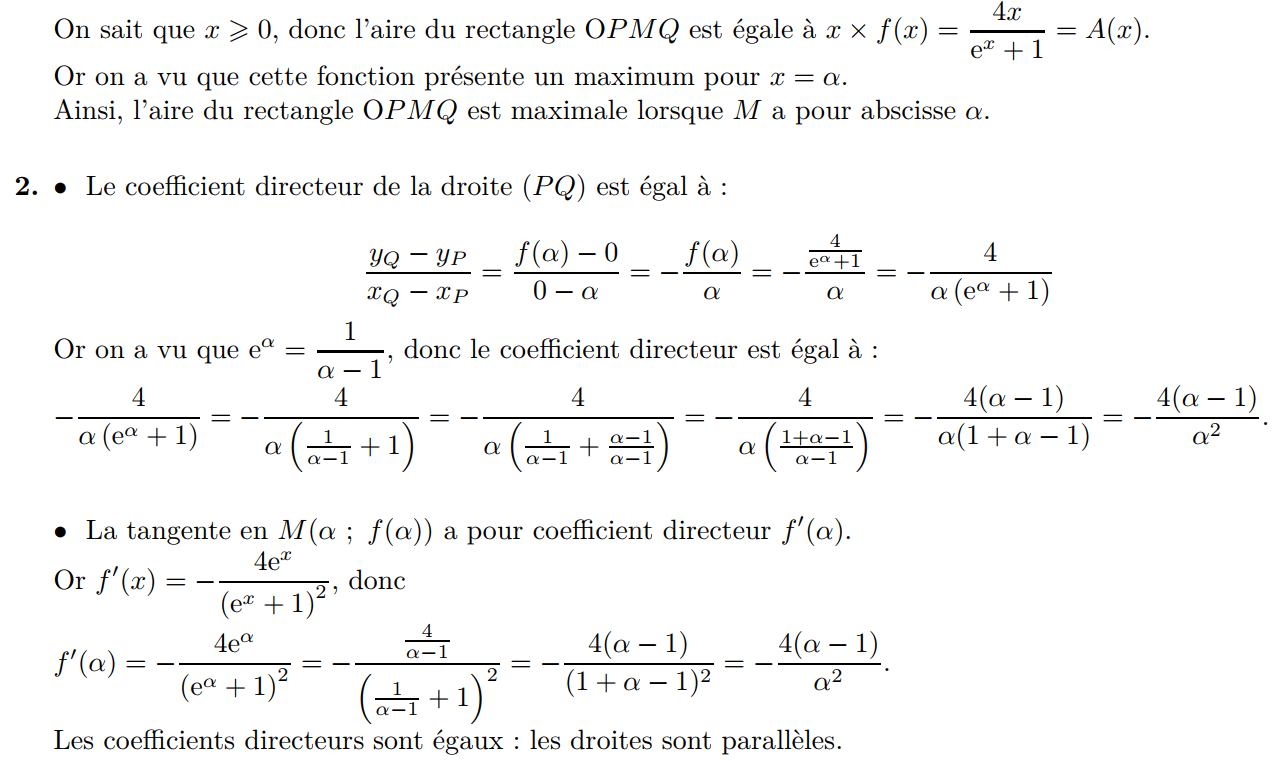
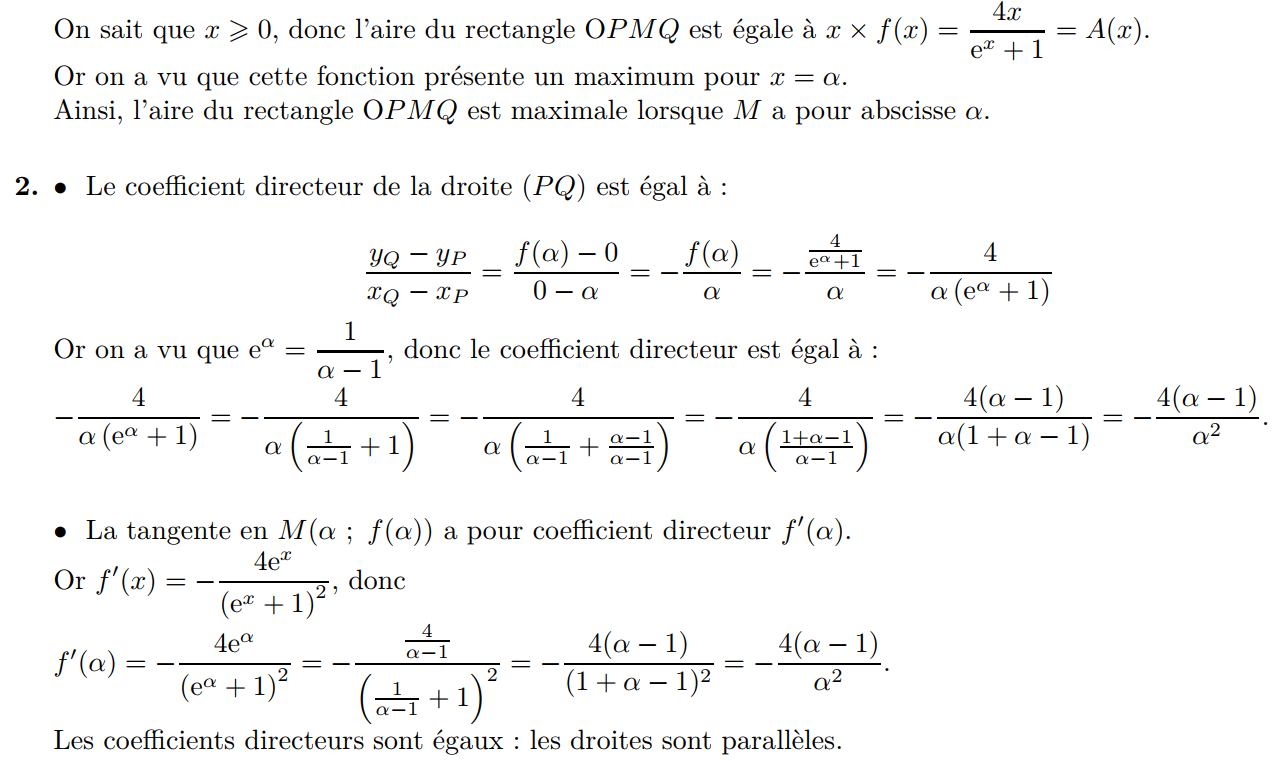
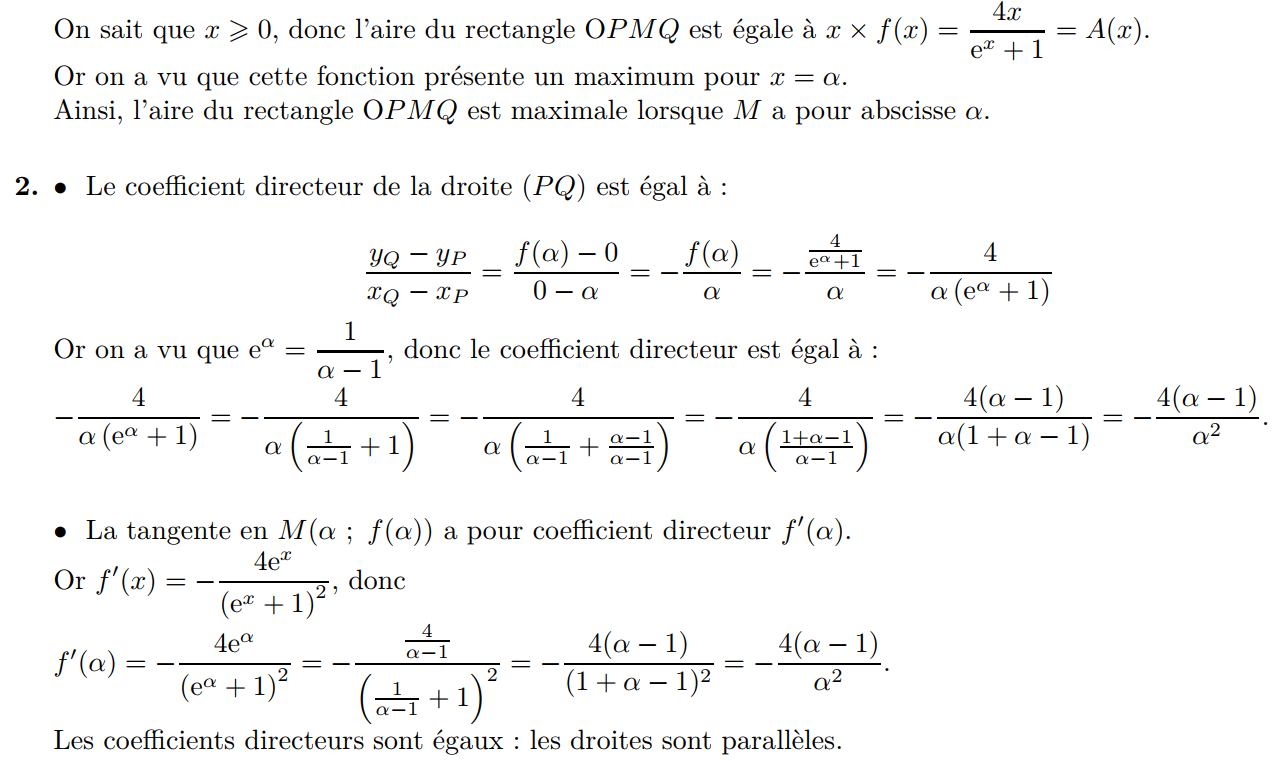
Ex 4 (fiche 2)

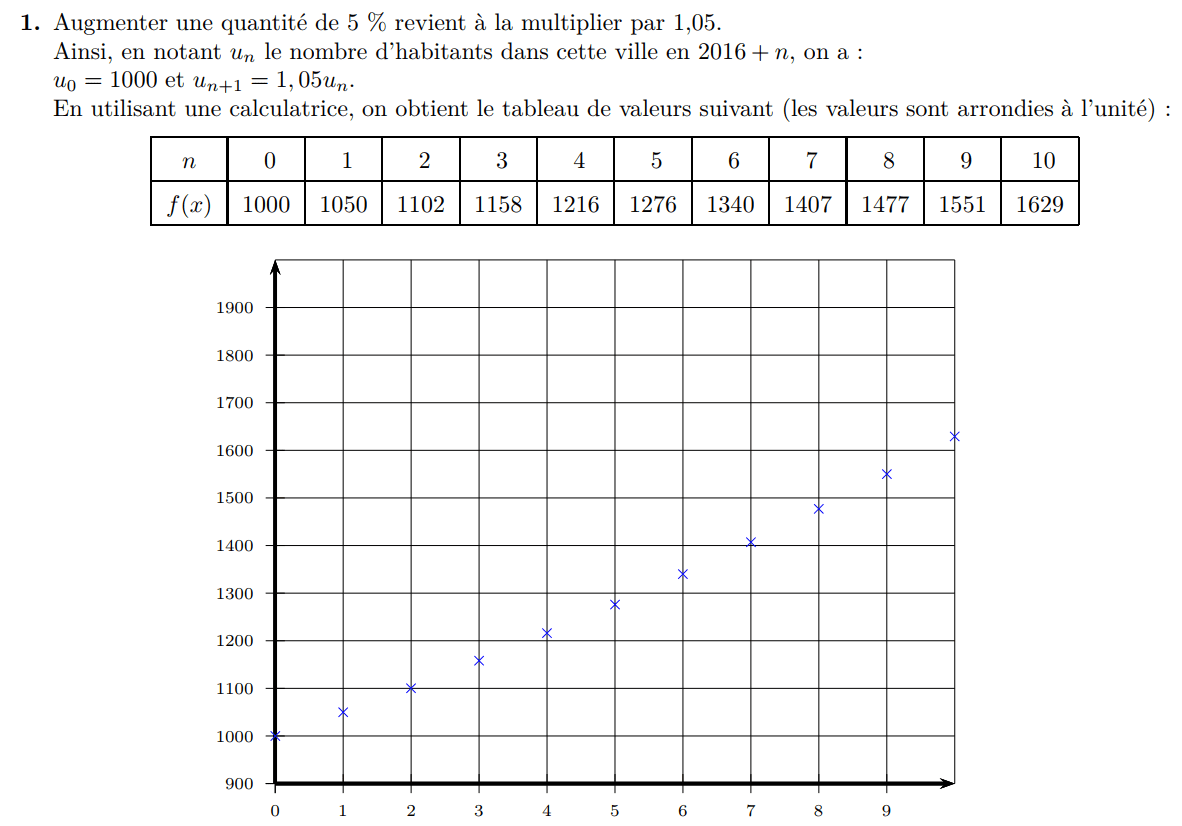


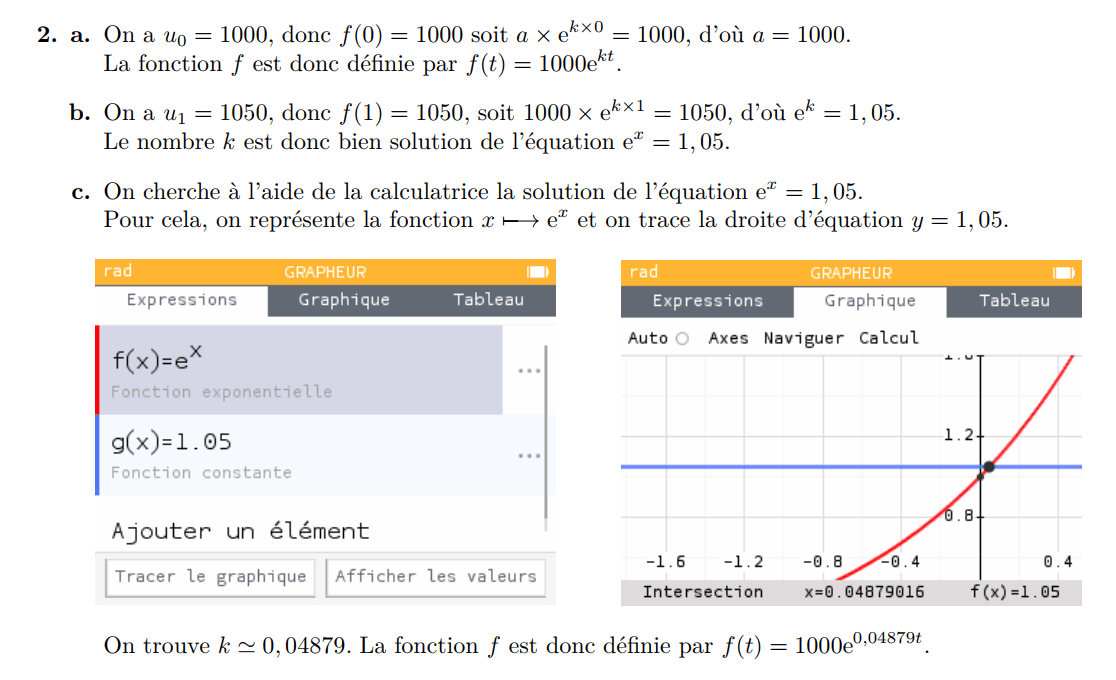




Exercices supplémentaires...
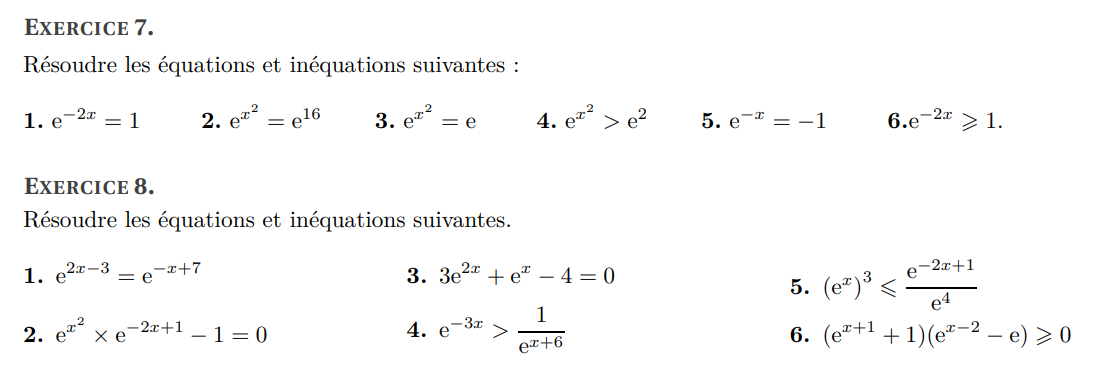



Résoudre des équations ou des inéquations :

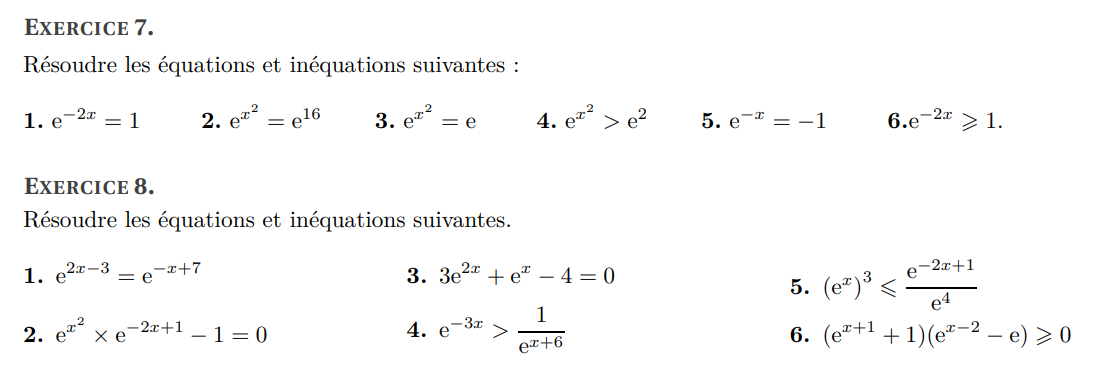
Résoudre des équations ou des inéquations :


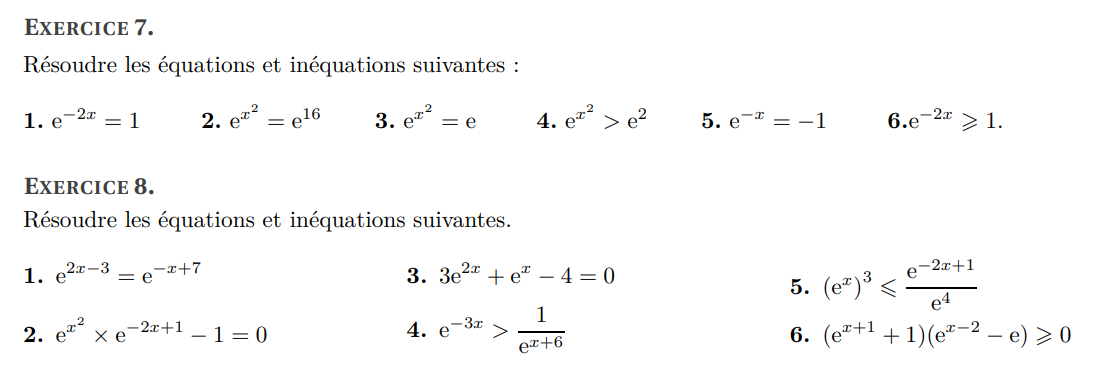
Résoudre des équations ou des inéquations :
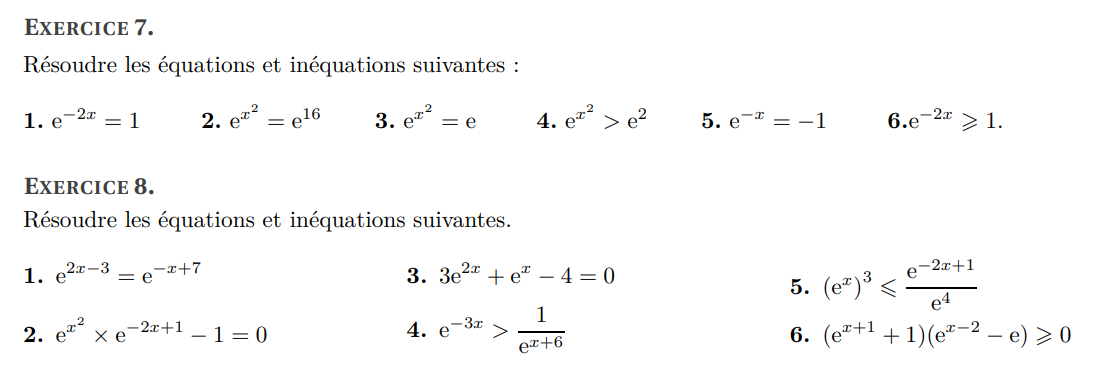
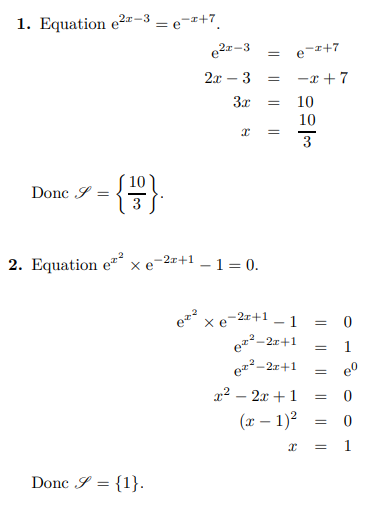
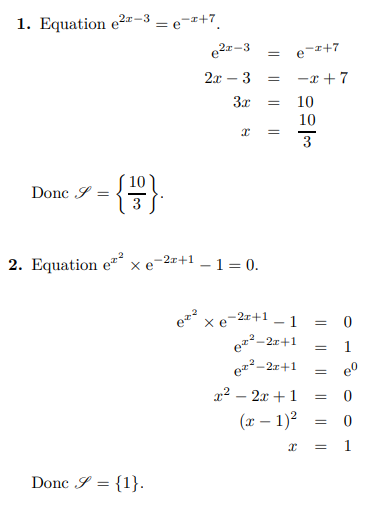
Résoudre des équations ou des inéquations :

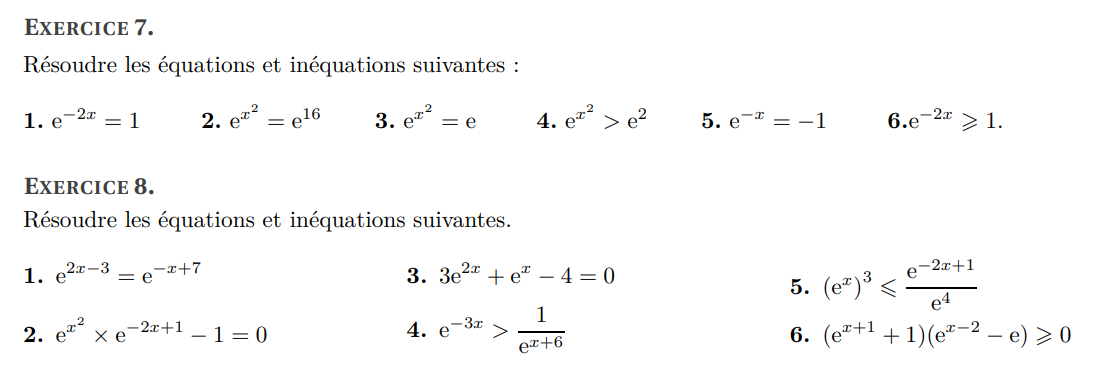
Résoudre des équations ou des inéquations :


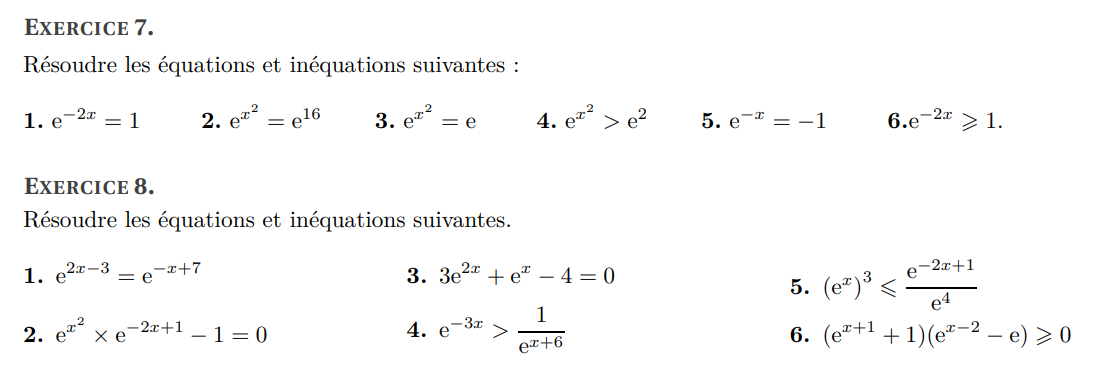
Résoudre des équations ou des inéquations :


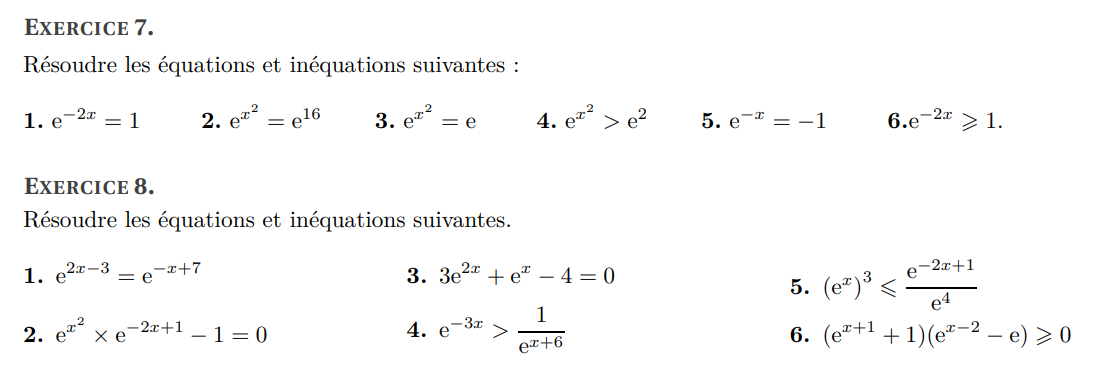
Résoudre des équations ou des inéquations :



Étudier des fonctions :

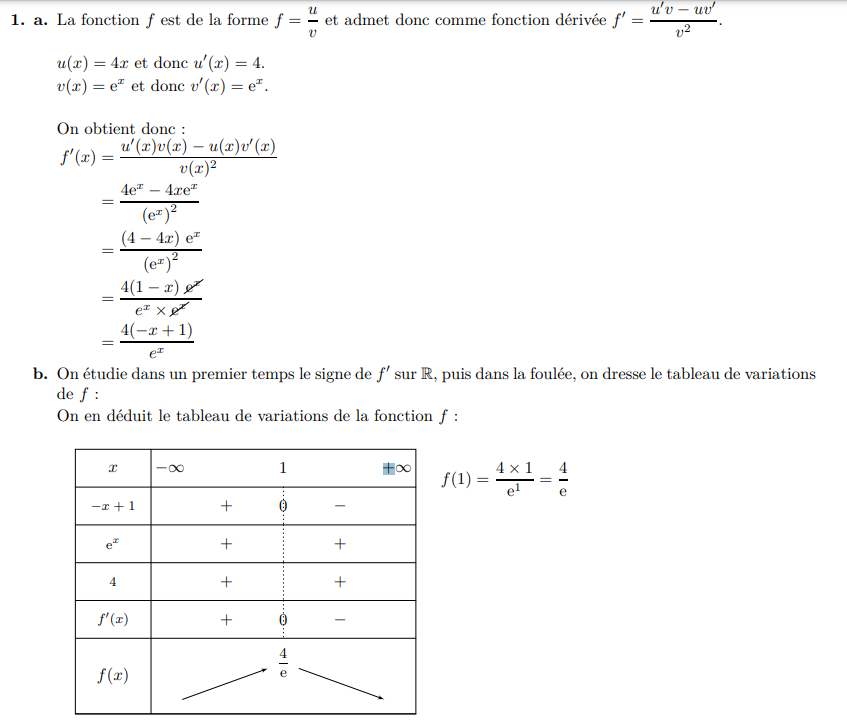
Étudier des fonctions :



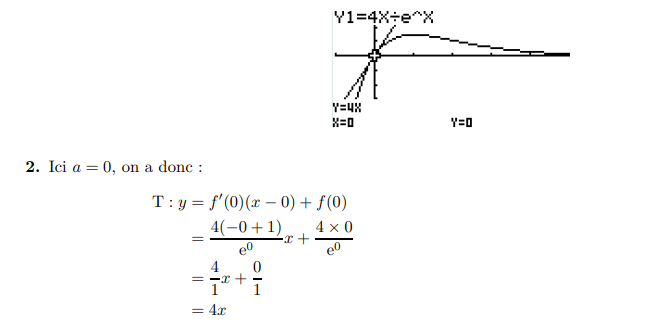




Étudier des fonctions :



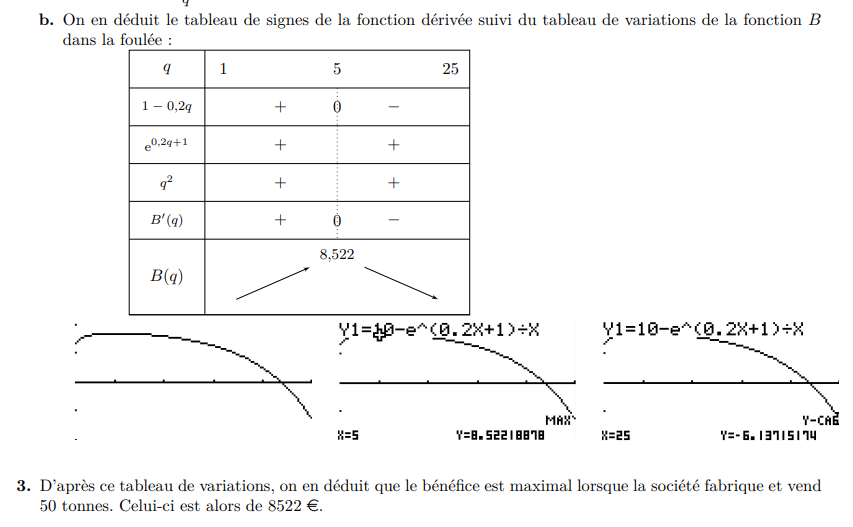



Résumé :