Nombres et calculs

Les différents types de nombres

les nombres entiers naturels : ℕ= {0 ; 1 ; 2 ; 3 ; 4...}

les nombres entiers relatifs : ℤ = {... − 3 ; −2 ; −1 ; 0 ; 1 ; 2 ; 3 ...}

les nombres décimaux : 0,17 ∈ ⅅ 2 ∈ ⅅ

\frac{1}{3}

les nombres rationnels : ∈ ℚ 5 ∈ ℚ

\frac{2}{3}

\sqrt{2}

les nombres réels : Tous les nombres rationnels, irrationnels sont des nombres réels. Leur ensemble est noté ℝ

∉ ⅅ

∉ ℚ

−1,5∈ ℝ

\frac{1}{3}

∈ ℝ

− ∈ ℝ

\sqrt{2}

\frac{5}{2}

∈ ℝ

4,7∈ ℝ

∈ ℝ

\pi

\dfrac{1}{3}\notin\mathbb{D}.

Démontrons par l'absurde que

Supposons que et démontrons que l'on arrive à une contradiction.

\dfrac{1}{3}\in\mathbb{D}

Démonstration :

\text{On suppose qu'il existe un nombre }a\in\mathbb{Z}\;et\;un\;nombre\;n\in\mathbb{N}

\text{On en déduit que }10^n\text{ est un multiple de 3 ce qui est absurde.}

\dfrac{1}{3}\notin\mathbb{D}.

On en conclut que

\text{Avec l'égalité des produits en croix on obtient }3a= 10^n.

\text{tels que }\dfrac{1}{3}=\dfrac{a}{10^n}.

K(-1)\,;L\left(-\dfrac{2}{3}\right)\,;M\left(\dfrac{1}{3}\right)

N(1,5)\,;O\left(\dfrac{7}{3}\right)\,;P(3)

La contraposée d'une proposition

Proposition :

Si un triangle ABC est rectangle en A

alors \(BC^2= AB^2+AC^2\).

Si \(BC^2\neq AB^2+AC^2\)

alors le triangle ABC n'est pas rectangle en A

Contraposée de la proposition :

Si A alors B (on note \(A\Rightarrow B\) )

Proposition :

Contraposée de la proposition :

plus généralement :

Si non B alors non A (on note \(\overline{B}\Rightarrow \overline{A}\) )

Propriété (admise) : Si la contraposée d'une propriété est vraie alors la propriété est vraie

Comment caractériser un nombre pair ?

2 \times 0 = 0

2 \times 1= 2

2 \times 2= 4

...

2 \times 3= 6

2 \times k \text{ avec }k \text{ entier}

\text{Il est de la forme } 2 k \text{ avec }k \text{ entier}

Comment caractériser un nombre impair ?

2 \times 0+1 = 1

2 \times 1+1=3

2 \times 2+1= 5

...

2 \times 3+1=7

2 \times k +1\text{ avec }k \text{ entier}

\text{Il est de la forme } 2 k +1\text{ avec }k \text{ entier}

Si \(a\) est un entier pair, que peut-on dire de \(a^2\) ?

Soit \(a\) un nombre entier.

Si \(a^2\) est pair, que peut-on dire de \(a\) ?

\(a^2\) est pair.

\(a\) est pair.

C'est le résultat que nous allons démontrer...

lemme

Si \(a^2\) est pair alors \(a\) est pair.

Proposition :

Contraposée de la proposition :

Si \(a\) est impair alors \(a^2\) est impair.

Pour démontrer la proposition nous allons prouver que sa contraposée est vraie.

Nous allons considérer un nombre impair et montrer que son carré est aussi un nombre impair.

Soit \(a\) un nombre impair. Il existe un entier relatif \(k\) tel que \(a=2k+1\).

Donc \(a^2=(2k+1)^2=4k^2+4k+1=2(2k^2+2k)+1\).

Si on note \(n=(2k^2+2k)\), \(a^2\) est de la forme \(2n+1\) avec \(n\) entier.

Donc \(a^2\) est un nombre impair.

Nous avons démontré par contraposée que si \(a^2\) est un nombre pair alors \(a\) est un nombre pair.

\sqrt{2}\notin \mathbb{Q}.

Démontrons par l'absurde que

Supposons que

\sqrt{2}\in \mathbb{Q}

c'est à dire qu'il existe un nombre

Démonstration :

a\in\mathbb{Z}\;et\;un\;nombre\;b\in\mathbb{N^*}\;tels\;que\;\sqrt{2}=\dfrac{a}{b}

avec\;\dfrac{a}{b}\, une \;fraction\; irréductible.

\text{En élevant au carré, on obtient }2=\dfrac{a^2}{b^2}.

On en déduit que \(a^2\) est pair.

Donc d'après le lemme a est pair .

\text{Ainsi il existe un entier }p\text{ tel que }a=2p.

\text{Ce qui équivaut à }a^2=2b^2.

a^2=2b^2\text{ peut donc s'écrire } (2p)^2=2b^2

\text{On obtient }2b^2=4p^2\text{ d'où }b^2=2p^2

ce qui est absurde car la fraction

\(\dfrac{a}{b}\) est irréductible.

\sqrt{2}\notin \mathbb{Q}.

On en déduit que \(b^2\) est pair.

Donc d'après le lemme b est pair .

\text{Ainsi il existe un entier }q\text{ tel que }b=2q.

\text{On a donc }\sqrt{2}=\dfrac{a}{b}=\dfrac{2p}{2q}=\dfrac{p}{q}

On en conclut que

1)\;\dfrac{1}{2}=0,5 =\dfrac{5}{10^1}\; \text{donc}\; \dfrac{1}{2}\in \mathbb{D}.

2)\;\sqrt{5}\in \mathbb{R}\;

(\sqrt{5}\notin \mathbb{Q}\;\text{voir la démonstration pour}\; \sqrt{2})

Méthode : pour montrer qu'un nombre est décimal, l'écrire sous la forme :

\dfrac{a}{10^n}\;avec\;a\in\mathbb{Z}\;et\;\;n\in\mathbb{N}.

\sqrt{5}\notin \mathbb{Q}.

Démontrons par l'absurde que

Supposons que

\sqrt{5}\in \mathbb{Q}

c'est à dire qu'il existe un nombre

Démonstration :

a\in\mathbb{Z}\;et\;un\;nombre\;b\in\mathbb{N^*}\;tels\;que\;\sqrt{5}=\dfrac{a}{b}

avec\;\dfrac{a}{b}, une \;fraction\; irréductible.

\sqrt{5}=\dfrac{a}{b}\Leftrightarrow5=\dfrac{a^2}{b^2}\Leftrightarrow a^2=5b^2

donc a² est un multiple de 5

donc a est un multiple de 5. Donc il existe un nombre

tel\;que\;a = 5p.

a^2=5b^2\Leftrightarrow (5p)^2=5b^2\Leftrightarrow 25p^2=5b^2\Leftrightarrow b^2 = 5p^2

p\in\mathbb{Z}

donc b² est un multiple de 5 donc b est un multiple de 5.

On en déduit qu'il existe un nombre

q\in\mathbb{N^*}\;tel\;que\;b = 5q.

\sqrt{5}=\dfrac{a}{b}=\dfrac{5p}{5q}=\dfrac{p}{q}

ce qui est absurde car la fraction

\dfrac{a}{b}

est irréductible. On en conclut que

\sqrt{5}\notin \mathbb{Q}.

3)\;\dfrac{10-4}{3}=2\; \text{donc}\; \dfrac{10-4}{3}\in \mathbb{N}.

4)\;-\sqrt{16}=-4\;\text{donc}\;-\sqrt{16} \in \mathbb{Z}\;

1)\;\text{Toujours vraie. En effet, si } x \in \mathbb{N}\;\text{alors } 2x \in \mathbb{N}

\;\text{et } 2x+1\in\mathbb{N}.

2)\;\text{Toujours vraie. En effet, }\mathbb{N}\subset\mathbb{Q}\; et\; 2x+1 \in \mathbb{N}

donc\;2x+1 \in \mathbb{Q}.

3)\;\text{Faux. En effet, si } x=2\;\text{alors } 3x-7=-1 \;et\; -1\notin \mathbb{N}.

4)\;\text{Faux. En effet, si }x=1\;alors\;\dfrac{x-6}{2}=-2,5

3x-7\in \mathbb{Z}

\;et\;-2,5...\notin \mathbb{Z}.

\dfrac{x-6}{2}=\dfrac{5(x-6)}{10}\;avec\;5(x-6)\in \mathbb{Z}.

\text{On en déduit que } \dfrac{x-6}{2}\in \mathbb{D}.

5) Vrai : tous les nombres rencontrés en seconde sont des nombres réels.

6)\;\text{Faux. En effet, si } x=2\;\text{alors } \sqrt{2}\notin \mathbb{Q}.\; \sqrt{x}\in\mathbb{R}.

1) -5=\dfrac{-5}{10^0}\;donc\;-5\in\mathbb{D}.

3) \dfrac{3}{40}=\dfrac{75}{10^3}\;donc\;\dfrac{3}{40}\in\mathbb{D}.

2) \dfrac{5}{7}\notin\mathbb{D}.\;\text{Voir la démonstration pour }\dfrac{1}{3}.

4) \dfrac{40}{3}\notin\mathbb{D}.\;\text{Voir la démonstration pour }\dfrac{1}{3}.

\dfrac{5}{7}\notin\mathbb{D}.

Démontrons par l'absurde que

Supposons que

\dfrac{5}{7}\in\mathbb{D}

c'est à dire qu'il existe un nombre

Démonstration :

a\in\mathbb{Z}\;et\;un\;nombre\;n\in\mathbb{N}\;tels\;que\;\dfrac{5}{7}=\dfrac{a}{10^n}\Leftrightarrow 7a=5\times 10^n.

Donc\;5\times10^n

est un multiple de 7 ce qui est absurde.

\dfrac{5}{7}\notin\mathbb{D}.

On en conclut que

1) Faux. En effet,

5-7=-2.

3) Faux. En effet,

\dfrac{\sqrt{3}}{2}\notin \mathbb{Q}.

2) Faux. En effet,

\dfrac{1}{3}\notin \mathbb{D}.

4) Vrai. En effet, si

n\in \mathbb{Z},\; a \in \mathbb{Z}

n\times\dfrac{a}{b}=\dfrac{na}{b}\in \mathbb{Q}.

et\;b\in \mathbb{N^*},

1) 3² + 4² = 5² donc d'après la réciproque du théorème de Pythagore le triangle est rectangle. 3 et 4 sont des entiers consécutifs donc le triangle rectangle est presque isocèle.

2) Soit un triangle rectangle presque isocèle. Soit n le nombre entier correspondant à la longueur du petit côté de l'angle droit. L'autre coté de l'angle droit est alors n + 1.

D'après le théorème de Pythagore l'hypoténuse a donc pour longueur

\sqrt{n^2+(n+1)^2}

Nous devons donc élaborer un algorithme qui renvoie trois nombres :

n, n+1\;et\;\sqrt{n^2+(n+1)^2}

est un nombre entier.

Pour n allant de 1 à 9999 (on fixe arbitrairement un seuil)

si \;\sqrt{n^2+(n+1)^2}

est un nombre entier

si \;\sqrt{n^2+(n+1)^2}

afficher\;n\;,\;n+1\;et \;\sqrt{n^2+(n+1)^2}.

Algorithme :

Programmation de l'algorithme en Python

x\in[7\;;20]

7\leqslant x\leqslant 20

49\leqslant 7x\leqslant 140

\times 7

7x\in[49\;;140]

x\in[7\;;20]\Leftrightarrow 7x\in[49\;;140]

x\in[7\;;20]\text{ si et seulement si } 7x\in[49\;;140]

x\in]-1\;;3]\text{ si et seulement si } 7-x\in[4\;;8[

x\in]-1\;;3]

-1< x\leqslant 3

1>-x\geqslant -3

\times (-1)

-3\leqslant -x<1

4\leqslant 7-x<8

x\in]-1\;;3]\Leftrightarrow 7-x\in[4\;;8[

x\in[-5\;;7]

-5\leqslant x\leqslant 7

\times 2

-10\leqslant 2x\leqslant 14

-7\leqslant 2x+3<17

x\in[-5\;;7]\Leftrightarrow 2x+3\in[-7\;;17]

x\in[-5\;;7]\text{ si et seulement si } 2x+3\in[-7\;;17]

-2x\in[1\;;+\infty[

-2x\geqslant 1

x\leqslant -\dfrac{1}{2}

x\in \left]-\infty\;;-\dfrac{1}{2}\right]

x\in \left]-\infty\;;-\dfrac{1}{2}\right]\text{ si et seulement si }-2x\in[1\;;+\infty[

\div (-2)

x\in \left]-\infty\;;-\dfrac{1}{2}\right]\Leftrightarrow -2x\in[1\;;+\infty[

3-x\in]-\infty\;;6]

x\in [ -3\;;+\infty[\Leftrightarrow 3-x\in]-\infty\;;6]

3-x\leqslant 6

-x\leqslant 3

x\geqslant -3

\times (-1)

-3

x\in [ -3\;;+\infty[

x\in [ -3\;;+\infty[\text{ si et seulement si } 3-x\in]-\infty\;;6]

7+2x\in[-1\;;1]

x\in[-4\;;-3] \Leftrightarrow 7+2x\in[-1\;;1]

-1\leqslant 7+2x\leqslant 1

-8\leqslant 2x\leqslant -6

\div 2

-7

-4\leqslant x\leqslant -3

x\in[-4\;;-3]

x\in[-4\;;-3] \text{ si et seulement si } 7+2x\in[-1\;;1]

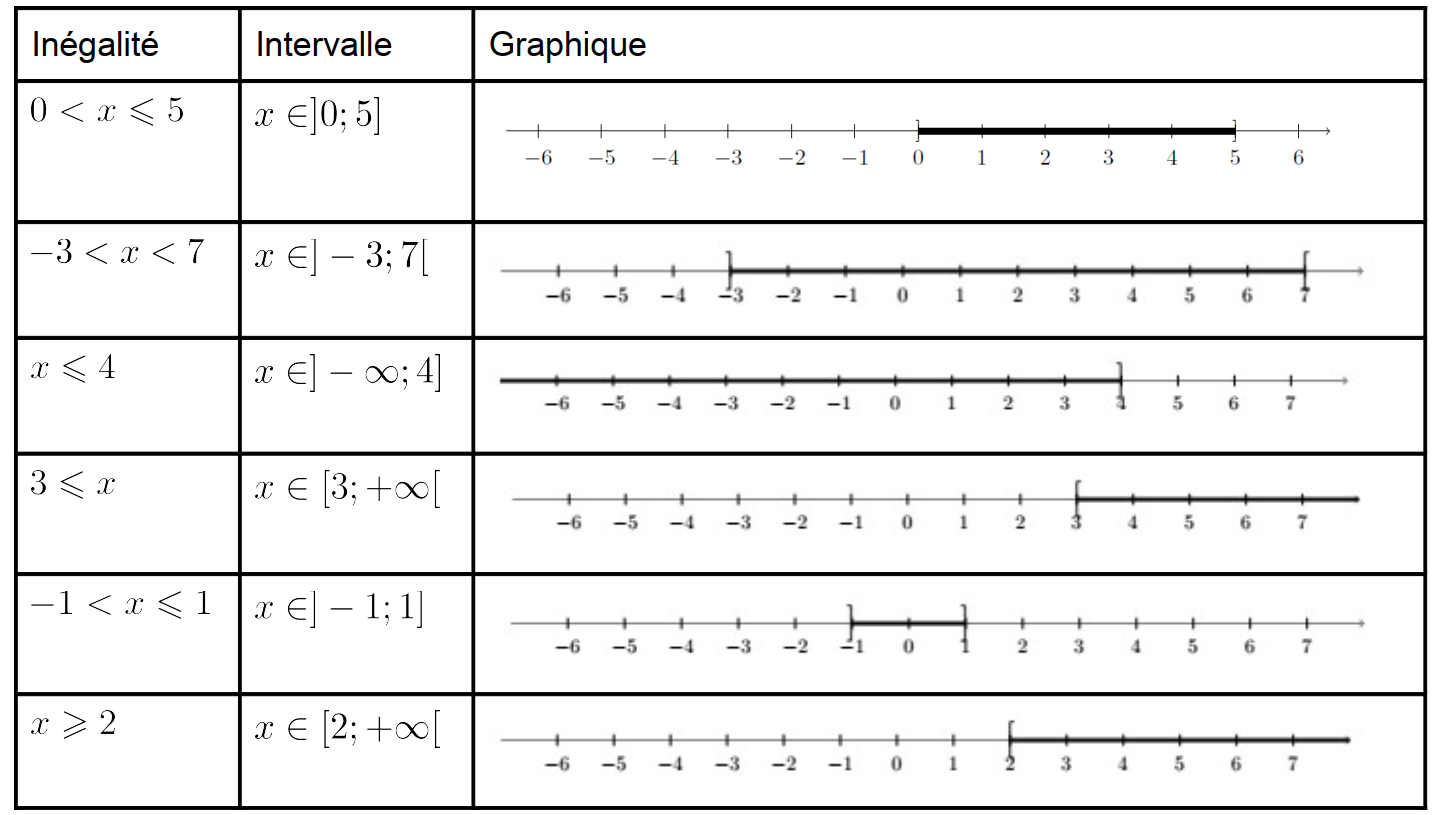
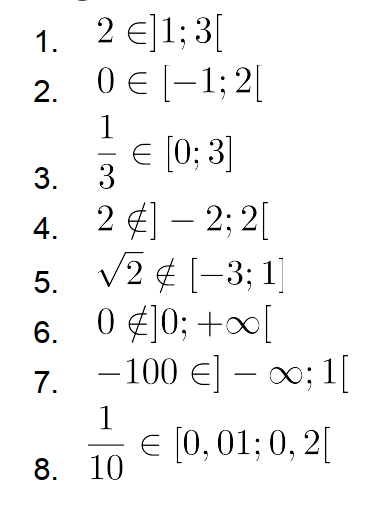
Intersection et réunion d'intervalles

• L’intersection de deux intervalles I et J est l’ensemble des réels appartenant à I et à J. On le note I ∩ J. Le ∩ se lit "inter".
• La réunion de deux intervalles I et J est l’ensemble des réels appartenant à I ou à J (ou éventuellement aux deux) On le note I ∪ J. Le ∪ se lit "union".

Exemples :

L'intersection est l’intervalle

"doublement" colorié

La réunion est l’intervalle

colorié : 1 ou 2 couleur(s)

Automatismes :

I = ]-2~;~4[

J = [1~;~5]

\text{Déterminer }I\cap J \text{ et }I\cup J

-2

[

]

[

]

I\cap J =[1~;~4[

I\cup J =]-2~;~5]

Automatismes :

I = [-1~;~3]

J = ]2~;~+\infty[

\text{Déterminer }I\cap J \text{ et }I\cup J

-1

[

]

I\cap J =]2~;~3]

I\cup J =[-1~;~+\infty[

x\leqslant 0

x\in ]-\infty\;;0]\cup [3\;;+\infty[

[

]

\;x\geqslant 3

On traduit les inégalités avec des intervalles.

C'est le ou qui indique que \(x\) appartient à la réunion des deux intervalles.

x\in [3\;;+\infty[

x\in ]-\infty\;;0]

\;x-6>0

5x\leqslant5

x\in ]-\infty\;;1]\cup ]6\;;+\infty[

]

x> 6

x\in ]6\;;+\infty[

x\leqslant 1

x\in ]-\infty\;;1]

x\leqslant 2

-4x\leqslant -20

x\in ]-\infty\;;2]\cup [5\;;+\infty[

[

]

x\in ]-\infty\;;2]

x\geqslant5

x\in [5\;;+\infty[

[4\;;+\infty[\cup [3\;;+\infty[=[3\;;+\infty[

[

x\geqslant 3

3x\geqslant 12

x\in [3\;;+\infty[

x\geqslant 4

x\in [4\;;+\infty[

x\in [3\;;+\infty[

7x-4\geqslant 3

1-x>0

]-\infty\;;1[\cup [1\;;+\infty[= ]-\infty\;;+\infty[

[

7x\geqslant 7

x\geqslant 1

x\in [1\;;+\infty[

-x>-1

x<1

x\in ]-\infty\;;1[

\;x\in ]-\infty\;;+\infty[

1-x>-3

x\in ]-\infty\;;3]

]-\infty\;;4[\cup ]-\infty\;;3]= ]-\infty\;;4[

[

]

-x>-4

x\in ]-\infty\;;4[

x<4

2x+1\leqslant 7

2x\leqslant 6

x\leqslant 3

x\in ]-\infty\;;4[

a>-6

On passe d'abord des inégalités aux intervalles.

]-\infty\;;3[\cap ]-6\;;+\infty[= ]-6\;;3[

-6

]

a<3

a\in ]-\infty\;;3[

x\in ]-6\;;+\infty[

Le et indique que a appartient à l'intersection des deux intervalles.

a\in ]-6\;;3[

]-\infty\;;7]\cap [-5\;;+\infty[ = [-5\;;7]

a\in [-5\;;+\infty[

a\in ]-\infty\;;7]

-5

[

]

a\geqslant-5

-a\geqslant - 7

a\leqslant 7

a\in [-5\;;7]

a\in \left[\dfrac{1}{3}\;;1\right[

a<1

3a-1\geqslant 0

\dfrac{1}{3}

[

2a+1<3

2a<2

a\in ]-\infty\;;1[

a\geqslant \dfrac{1}{3}

3a\geqslant 1

a\in \left[\dfrac{1}{3}\;;+\infty\right[

]-\infty\;;1[\cap \left[\dfrac{1}{3}\;;+\infty\right[= \left[\dfrac{1}{3}\;;1\right[

a>1

a\geqslant 3

a\in ]1\;;+\infty[\cap \left[3\;;+\infty\right[\Leftrightarrow a\in \left[3\;;+\infty\right[

]

[

3(2-a)<3

2-a<1

-a<-1

a\in ]1\;;+\infty[

a-1\geqslant2

a\in [3\;;+\infty[

Valeur absolue

Soit \(x\) et \(a\) deux nombres réels.

La valeur absolue de \(x-a\), notée \(|x-a|\) est la distance entre \(x\) et \(a\) sur la droite des réels.

|5-3|=|3-5|=2

|2|=|-2|=2

La valeur absolue de \(x\), \(|x|=|x-0|\), est la distance entre \(x\) et \(0\) sur la droite des réels.

-2

|2|=|-2|=2

-2

Si \(x\) est positif \(|x|=x\)

Si \(x\) est négatif \(|x|=-x\)

Une valeur absolue est toujours positive (c'est une distance)

|2|=2

|-2|=-(-2)=2

\(|-5|=5\)
\(|\dfrac{-2}{-3}|=\dfrac{2}{3}\)
\(|-\sqrt{289}|=\sqrt{289}= 17\)
\(|3-\dfrac{2}{3}\times (6-4)|=\left|\dfrac{5}{3}\right|=\dfrac{5}{3}\)

La distance entre deux nombres réels est la valeur absolue de la différence de ces deux nombres.

\(|-2-(-12)|=|10|=10\)
\(\left|\dfrac{5}{3}-\dfrac{7}{6}\right|=\left|\dfrac{1}{2}\right|=\dfrac{1}{2}\)
\(|-\pi-2\pi|=|-3\pi|=3\pi\)
\(|-4-6|=\left|-10\right|=10\)

1. Quels sont les nombres dont la valeur absolue est 8 ?

x = 8 \text{ ou } x= -8

\text{L'équation }|x| = 8 \text{ admet deux solutions } -8\text{ et 8.}

\text{On note } S=\{-8~;~8\}

Ensemble des solutions

2. Quels sont les nombres dont la valeur absolue est \(-5\) ?

\text{L'équation }|x| = -5 \text{ n'admet pas de solution.}

\text{On note } S=\emptyset

Aucun

3. Quels sont les nombres dont la valeur absolue est 3 ?

x-1 = 3 \text{ ou } x-1=-3

S=\{-2~;~4\}

\(3\) et \(-3\).

x = 4 \text{ ou } x=-2

4. Quels sont les nombres dont la valeur absolue est 4 ?

2x+1 = 4 \text{ ou } 2x+1=-4

S=\{-2,5~;~1,5\}

\(4\) et \(-4\).

x = 1,5 \text{ ou } x=-2,5

2x = 3

2x = -5

1. \text{ Pour tout réel }x,\; 1+x^2\geqslant0.

Ainsi\;pour\;tout\;x\in \mathbb{R}, \;\;|1+x^2|=1+x^2.

La proposition est vraie.

2. Si \(k\) est un entier positif, \(|k|=k\).

La proposition est fausse.

4. \;pour\;tout\;n\in \mathbb{N}, \;n^2\geqslant n\;donc\;n^2-n\geqslant0.

Ainsi\;pour\;tout\;n\in \mathbb{N}, \;\;|n^2-n|=n^2-n.

La proposition est vraie.

3. \;pour\;tout\;x\in \mathbb{R}, \;-x^2\leqslant 0

La proposition est fausse.

a - r \leqslant x \leqslant a + r

a-r

a+r

|x-a|\leqslant r

x\in [a - r \,; a + r]

- r \leqslant x -a\leqslant r

1.\; |x-2|\leqslant 3

a-r

a+r

a - r \leqslant x \leqslant a + r

|x-a|\leqslant r

x\in [a - r \,; a + r]

2 - 3 \leqslant x \leqslant 2 + 3

x\in [ -1 \,; 5]

2.\; x\leqslant 15

3.\; |x|\leqslant 1

x\in [ -1 \,; 1]

- 1 \leqslant x \leqslant 1

4.\; 0\leqslant x\leqslant 2

x\in [0 \,; 2]

x\in ] -\infty \,; 15]

1.\; \dfrac{1}{7 }\approx 0,14286\;donc\;0,142\leqslant \dfrac{1}{7 }\leqslant 0,143

3.\; \sqrt{17}\approx 4,1231\;donc\;4,123\leqslant \sqrt{17}\leqslant 4,124

2.\; 0,758\leqslant 0,7586\leqslant 0,759

4.\; 2,356\times 10^{-3}=0,002356\; donc

0,002\leqslant 2,356\times 10^{-3}\leqslant 0,003

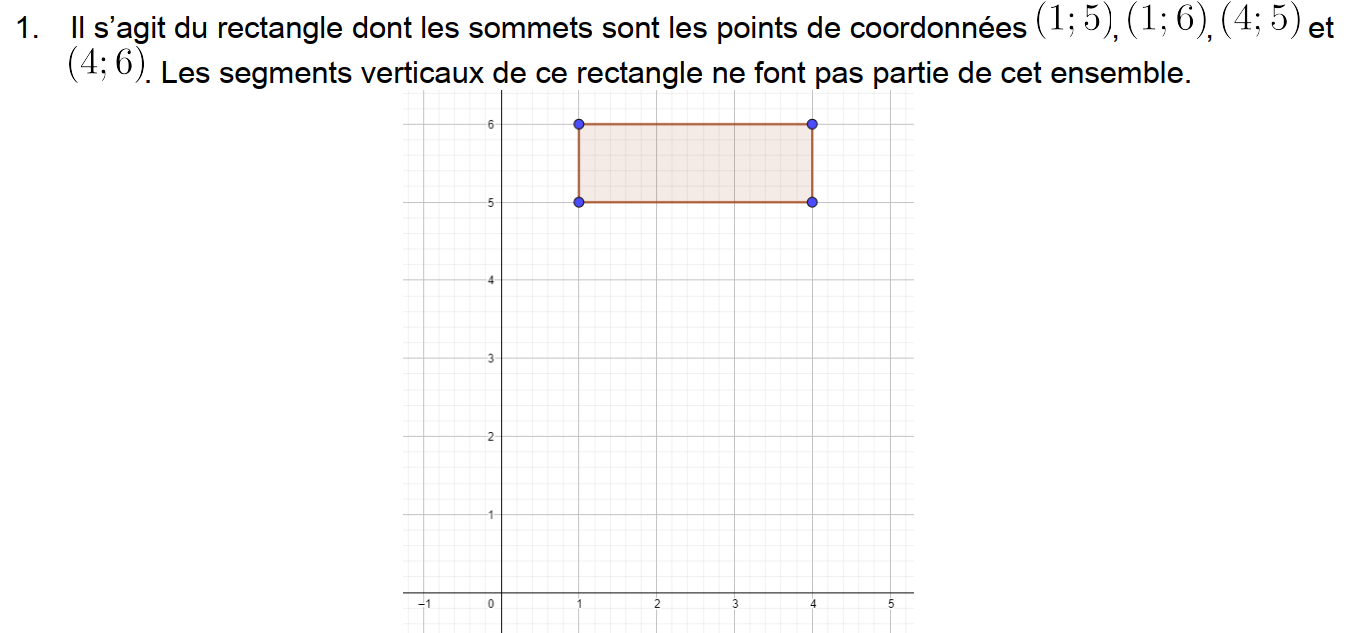
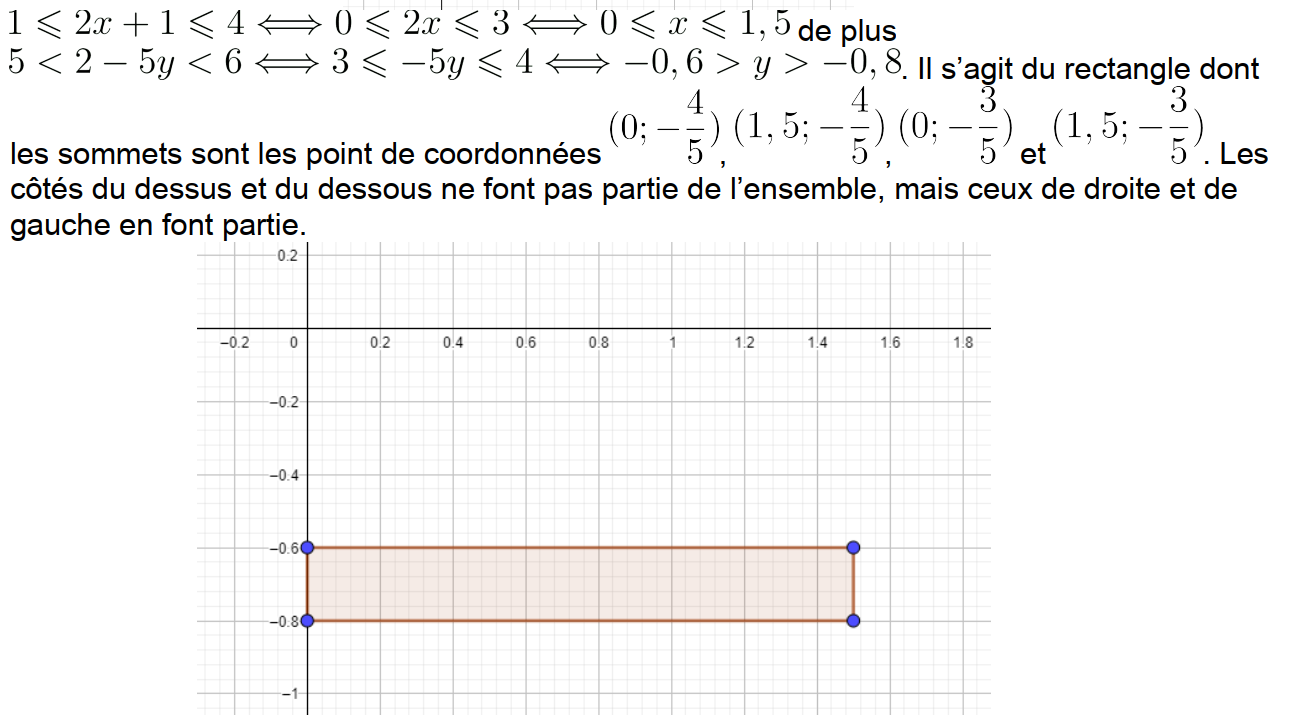
1. Soit a l'âge d'une personne.

a \in ]32\;;+\infty[

Condition pour rentrer au Macumba :

a \in [18\;;40]

Condition pour rentrer au La Playa :

a \in [18\;;40]\cap]32\;;+\infty[\Leftrightarrow a \in ]32\;;40]

Condition pour rentrer dans les deux clubs :

a \in [18\;;40]\cup]32\;;+\infty[\Leftrightarrow a \in [18\;;+\infty[

2. Condition pour rentrer dans l'un des deux clubs :