Configurations du plan : Exercices

Configurations du plan

1.\;ST^2=5,2^2= 27,04

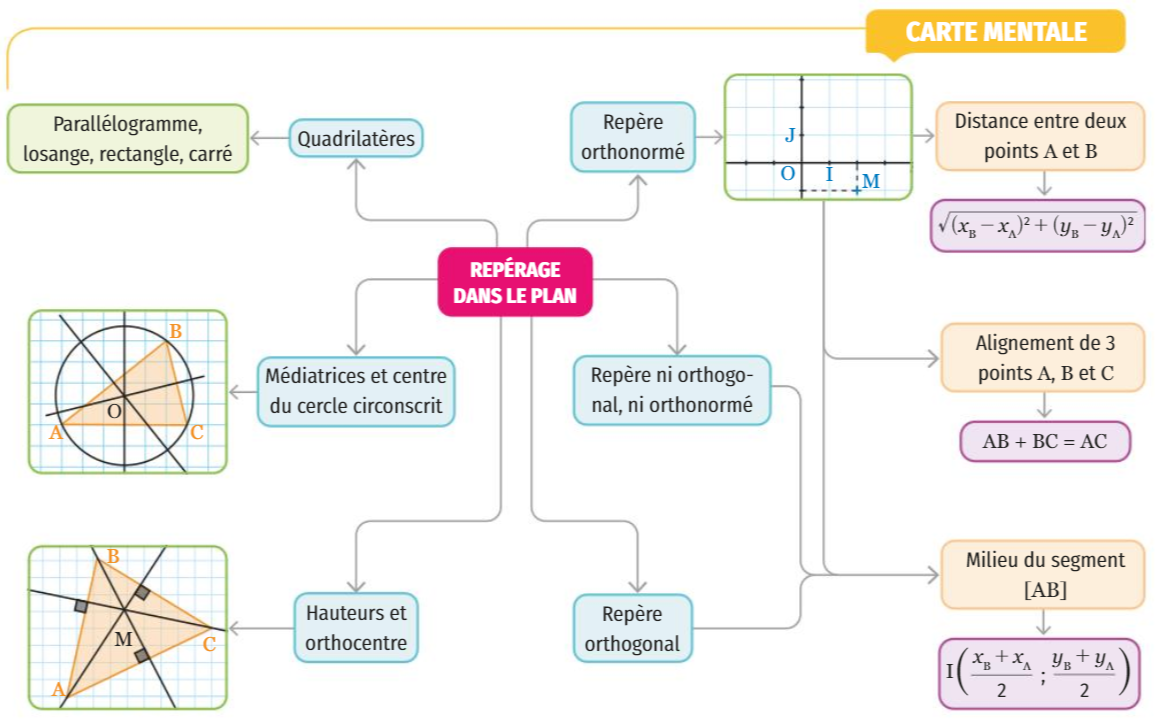
ST²=RS²+RT² donc d'après la réciproque du théorème de Pythagore, le triangle RST est rectangle en R.

2.\;\cos\hat{S}=\dfrac{RS}{ST}=\dfrac{4,8}{5,2}=\dfrac{12}{13}.

\hat{S}=\arccos\left(\dfrac{12}{13}\right)\approx 22,6°.

\hat{T}=90-\hat{S}\approx 67,4°\;;\hat{R}=90°.

RT^2+RS^2=27,04.

1.\;cos^2(M\hat{L}N)+sin^2(M\hat{L}N)=1

0,6^2+sin^2(M\hat{L}N)=1

0,36+sin^2(M\hat{L}N)=1

sin^2(M\hat{L}N)=1-0,36

sin^2(M\hat{L}N)=0,64

sin(M\hat{L}N)=\sqrt{0,64}

sin(M\hat{L}N)=0,8

2.\;\cos\hat{L}=\dfrac{LN}{LM}

0,6=\dfrac{LN}{10}

LN = 0,6\times 10 = 6 \;cm

\;\sin\hat{L}=\dfrac{MN}{ML}

0,8=\dfrac{MN}{10}

MN = 0,8\times 10 = 8 \;cm

MS^2=AM^2+AS^2

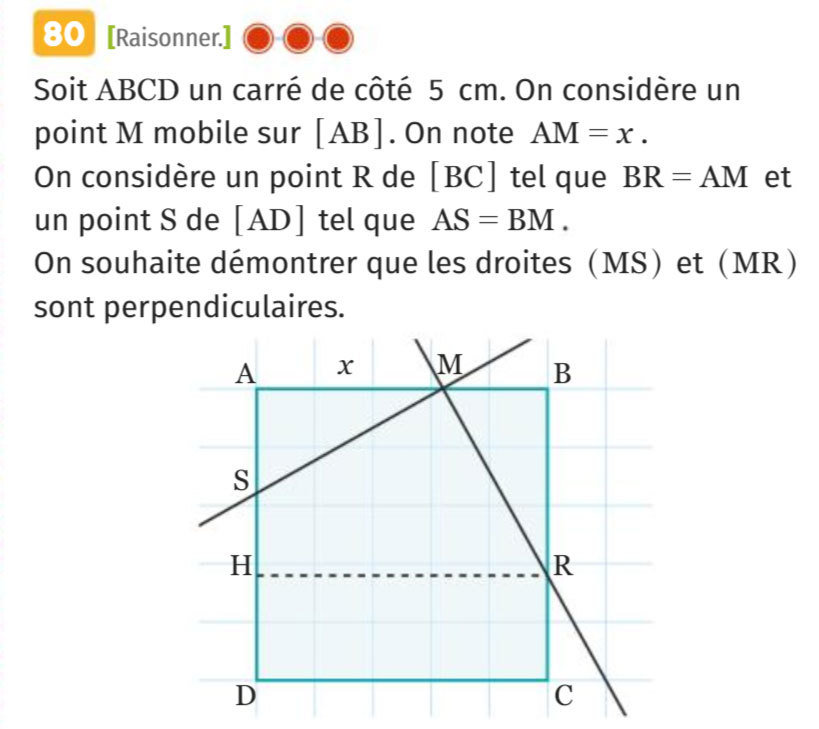
1. Le triangle MAS est rectangle en A, donc d'après le théorème de Pythagore on a

MS^2=x^2+(5-x)^2

MS^2=x^2+25-10x+x^2

MS^2=2x^2-10x+25

2. On a de même :

MR^2=2x^2-10x+25

3. a) H est le projeté orthogonal de R sur (AD) donc :

(RH)\perp (AD)

et\;H\in(AD).

S\in(AD)\;donc\;(SH)\perp(RH).

On en déduit que le triangle RSH est rectangle en H.

3. b)

AS = 5-x\;et\;AH = x\; donc

SH = AH-AS = x-(5-x)=2x-5.

RS^2=RH^2+SH^2.

3. c) Le triangle RSH est rectangle en H, donc d'après le théorème de Pythagore on a

On\;a\;donc\;RS^2=5^2+(2x-5)^2=4x^2-20x+50.

4. Conclusion :

MS^2=2x^2-10x+25\;et\;MR^2=2x^2-10x+25

donc \;MS^2+MR^2=4x^2-20x+50=RS^2.

D'après la réciproque du théorème de Pythagore, le triangle RSM est rectangle en M et donc

(MS)\perp (MR).

x^2=x^2-20x+100+4900

x^2=(x-10)^2+70^2

20x=5000

x=\dfrac{5000}{20}

x=250

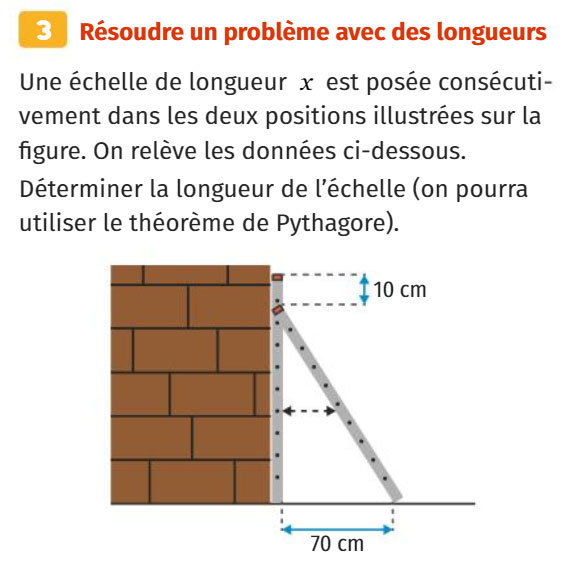
L'échelle mesure 2,5 m.

1. Si un parallélogramme a un angle droit alors c'est un rectangle.

Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.

2. Si un rectangle a deux côtés consécutif de même longueur alors c'est un carré.

Si un rectangle a ses diagonales perpendiculaires alors c'est un carré.

3. Oui un carré est a la fois un losange et un rectangle.

...\;\dfrac{2,7}{499,7}=\dfrac{1,75}{h}

h=\dfrac{1,75\times 499,7}{2,7}\approx 324 \;m

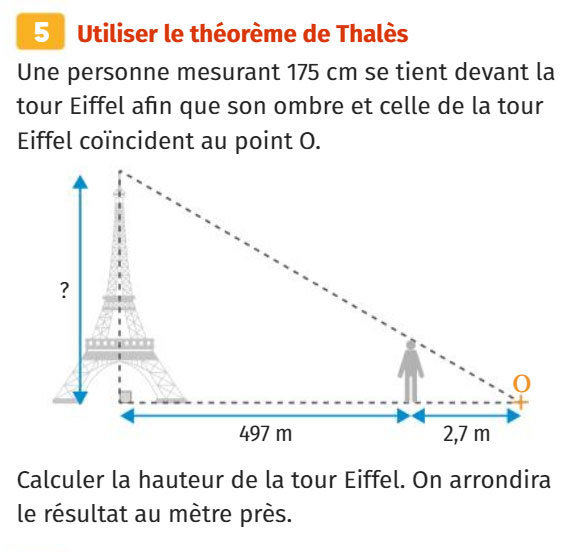
Géométrie repérée

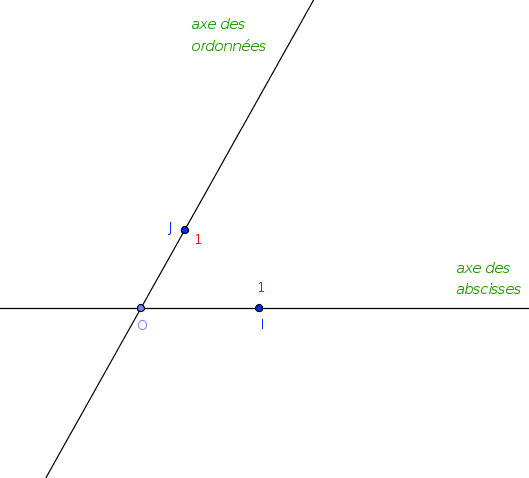
Un repère quelconque

Définir un repère du plan, c’est choisir 3 points non alignés dans un ordre précis : O, I, J.

On note ce repère (O, I , J)

(OI) :

(OJ) :

Origine du repère

Repères

Repère orthogonal

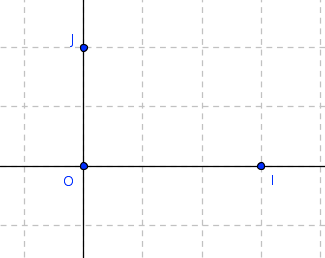
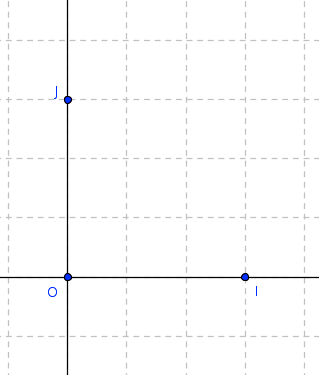
Des repères particuliers :

Repère orthonormé

(OI)⊥(OJ)

(OI)⊥(OJ) et OI = OJ

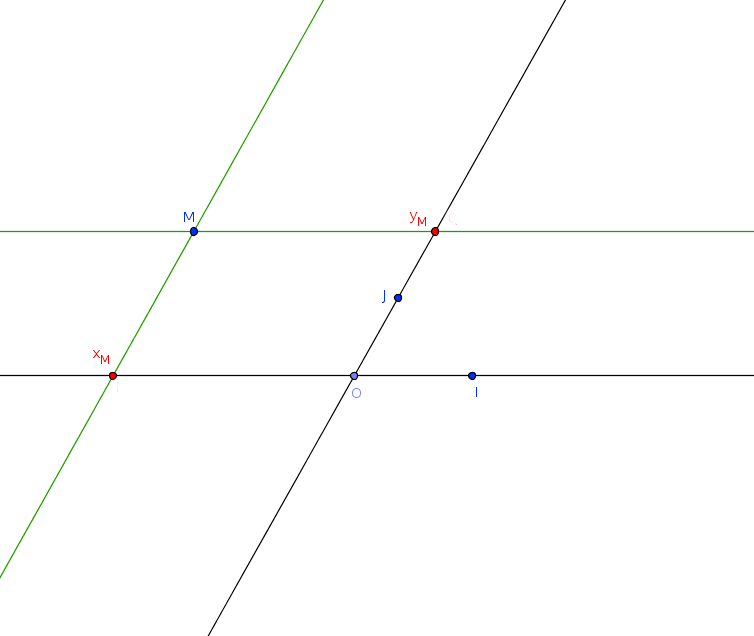
abscisse

du point M

ordonnée

du point M

(xM ; yM) : coordonnées du point M dans le repère (O, I , J).

Exemples : Dans le repère (O, I , J), on a :

O (0 ; 0) ; I (1 ; 0) ; J (0 ; 1) ; A (3 ; 2) ; B (−2 ; 3) et C (−1 ; −2).

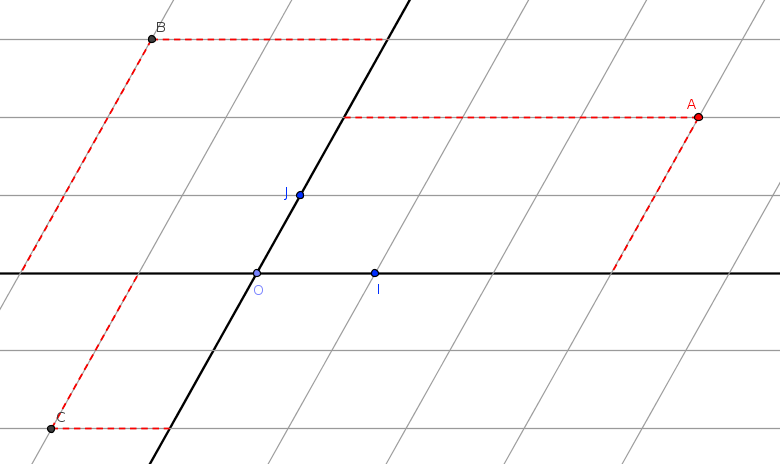
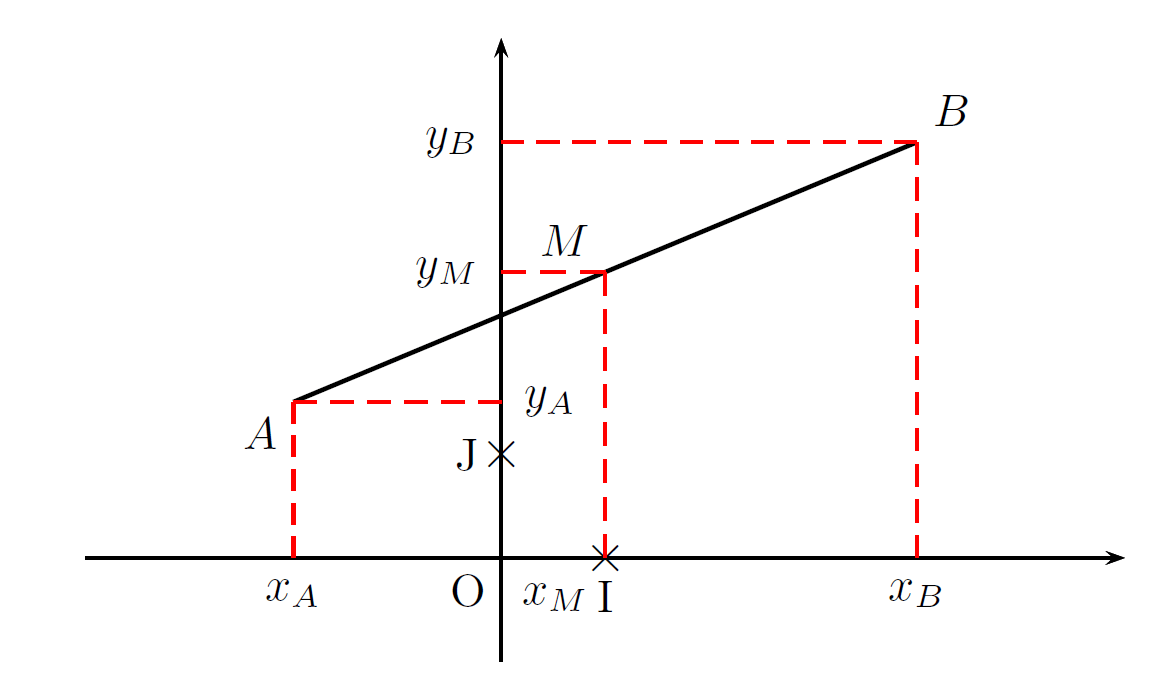
Coordonnées du milieu d’un segment

Soit (O, I , J) un repère du plan et A (xA ; yA) et B (xB ; yB) deux points du plan.

Les coordonnées du milieu I de [AB] sont :

x_I=\dfrac{x_A+x_B}{2}

y_I=\dfrac{y_A+y_B}{2}

I\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)

Exemples :

1) C(−5 ; 7) et E(9 ; −4) sont deux points du plan muni d'un repère (O ; I, J).

Calculer les coordonnées du milieu K du segment [CE].

x_K=\dfrac{-5+9}{2}

y_K=\dfrac{7+(-4)}{2}

x_K=\dfrac{4}{2}

y_K=\dfrac{3}{2}

x_K=2

K\left(2 ~;~1,5\right)

y_K=1,5

Exemples :

2) M(−1 ; 3) et K(2 ; −3) sont deux points du plan muni d'un repère (O ; I, J).
Soit N le point du plan tel que K soit le milieu du segment [MN]. Calculer les coordonnées du point N.

\dfrac{-1+x_N}{2}=2

\dfrac{3+y_N}{2}=-3

-1+x_N=4

3+y_N=-6

x_N=5

y_N=-9

N(5 ;-9)

Exemples :

3) A(−1 ; 2), B(1 ; 4) et C(7 ; −2) sont trois points du plan muni d'un repère (O ; I, J).
Calculer les coordonnées du point D tel que ABCD soit un parallélogramme.

Étape 1:

On calcule les coordonnées de K, le milieu de [AC], diagonale du parallélogramme ABCD.

x_K=\dfrac{-1+7}{2}

y_K=\dfrac{2+(-2)}{2}

x_K=\dfrac{6}{2}

y_K=\dfrac{0}{2}

x_K=3

y_K=0

Étape 2:

K étant aussi le milieu de la diagonale [BD], on a :

\dfrac{x_B+x_D}{2}=x_K

\dfrac{y_B+y_D}{2}=y_K

\dfrac{1+x_D}{2}=3

\dfrac{4+y_D}{2}=0

1+x_D=6

4+y_D=0

x_D=5

y_D=-4

K(3~;~0)

D(5~;~-4)

y_K=\dfrac{3+(-3)}{2}

y_K=0\text{ donc }K\in (OI).

A(1~;3)~;~C(3~;~-3)

x_L=\dfrac{1+(-2)}{2}

x_L=-0,5\neq 0\text{ donc }L\notin (OJ).

A(1~;3)~;~B(-2~;~0)

y_M=\dfrac{0+(-3)}{2}

y_M=-1,5\neq 0\text{ donc }M\notin (OI).

B(-2~;~0)~;~C(3~;~-3)

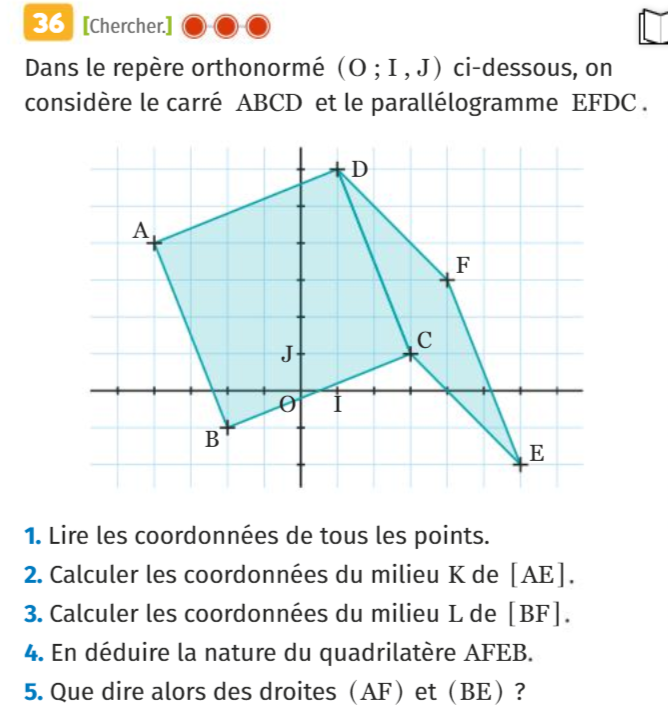
(A, B et C uniquement)

x_K=\dfrac{1,5+4}{2}=2,75

y_K=\dfrac{8+5}{2}=6,5

K\left(2,75 ~;~6,5\right)

Le point D est le symétrique du point A par rapport au point K si et seulement si le point K est le milieu de [AD] :

\dfrac{1+x_D}{2}=2,75

\dfrac{3+y_D}{2}=6,5

1+x_D=5,5

3+y_D=13

x_D=4,5

y_D=10

D\left(4,5 ~;~10\right)

Les diagonales [BC] et [AD] du quadrilatère ABCD ont le même milieu K donc ABCD est un parallélogramme.

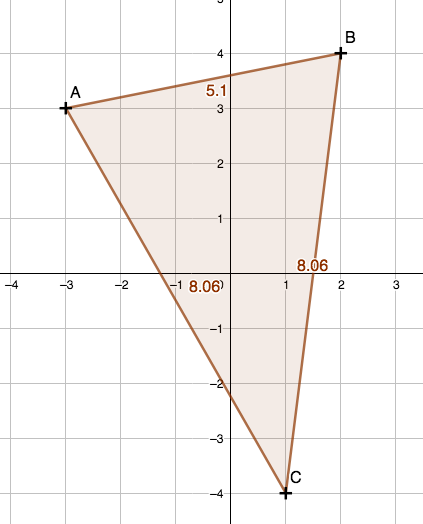
2. Le triangle ABC semble isocèle en C.

3.\; AC = \sqrt{(1+3)^2+(-4-3)^2}

AC = \sqrt{65}

BC = \sqrt{(1-2)^2+(-4-4)^2}

BC = \sqrt{65}

AC = BC\text{ donc le triangle ABC}

\text{est isocèle en C.}

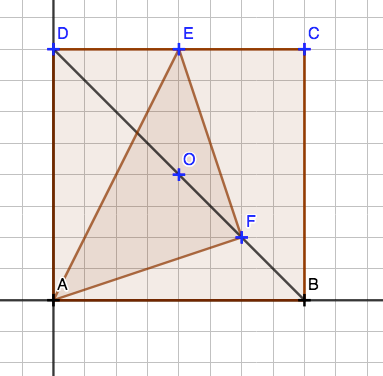
2. Dans le repère \( (A\;;B\;,D)\) on a :

A(0\;;0)\;;B(1\;;0)\;;D(0\;;1)\;;

C(1\;;1)\;;E\left(\dfrac{1}{2}\;;1\right)\;;F\left(\dfrac{3}{4}\;;\dfrac{1}{4}\right)\;;

O\left(\dfrac{1}{2}\;;\dfrac{1}{2}\right)\;;

3. Le repère étant orthonormé on peut utiliser la formule de calcul d’une distance :

EF = \sqrt{(x_F-x_E)^2+(y_F-y_E)^2}

EF = \sqrt{\left(\dfrac{3}{4}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}-1\right)^2}

EF = \sqrt{\left(\dfrac{1}{4}\right)^2+\left(-\dfrac{3}{4}\right)^2}

EF = \sqrt{\dfrac{10}{16}}=\sqrt{0,625}

\text{On a de même} \;AF = \sqrt{\dfrac{10}{16}}=\sqrt{0,625}\;et\;AE = \sqrt{\dfrac{5}{4}}=\sqrt{1,25}

4. D'après la question 3., \(EF=AF\) donc le triangle AEF est isocèle en F.

\text{On a de plus} \;AF^2+EF^2 = \dfrac{10}{16}+\dfrac{10}{16} =\dfrac{5}{4}=AE^2

donc d'après la réciproque du théorème de Pythagore le triangle AEF est rectangle en F.

Conclusion : le triangle AEF est isocèle rectangle en F.

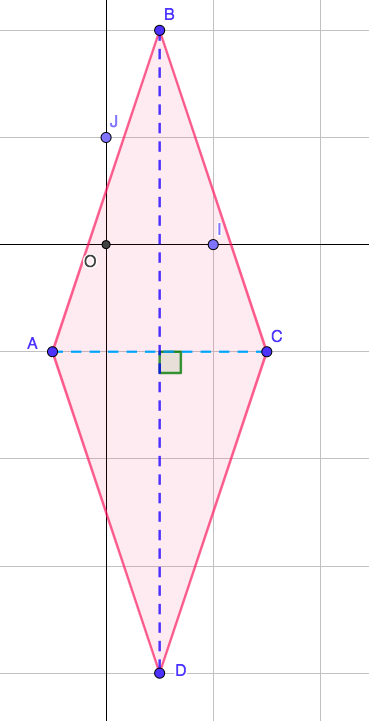
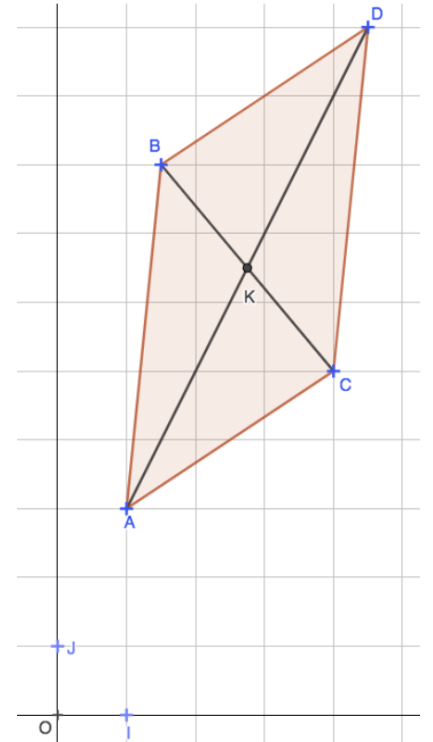
2. D’après la figure ci-contre, on peut conjecturer que le quadrilatère est un losange.

3. On peut montrer que [BD] et [AC] se coupent en leur milieu et que AB = BC...

Les points K et L sont confondus donc le quadrilatère ABCD est un parallélogramme.

AB = \sqrt{\left(\dfrac{1}{2}-\left(-\dfrac{1}{2}\right)\right)^2+\left(2-(-1)\right)^2}=\sqrt{1^2+3^2}=\sqrt{10}

BC = \sqrt{\left(\dfrac{3}{2}-\dfrac{1}{2}\right)^2+\left(-1-2\right)^2}=\sqrt{1^2+3^2}=\sqrt{10}

On a AB = BC ; Le parallélogramme ABCD a deux côtés consécutifs de même longueur donc c'est un losange.