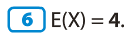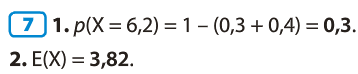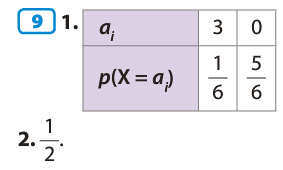Probabilités - Variables aléatoires

1 Quelques rappels

1.1 Loi de probabilité

Définition :

On appelle expérience aléatoire toute expérience ayant plusieurs issues (ou éventualités) possibles et dont on ne peut pas prévoir à l’avance laquelle de ces issues sera réalisée.
Ces éventualités sont notées e1 ; e2 ; . . . ; en.
Leur ensemble est noté  Ω est est appelé univers. On a donc
 Ω = {e1 ; e2 ; . . . ; en}.

Exemple : On lance un dé à 6 faces. L’univers est Ω = {1 ; 2 ; 3 ; 4 ; 5 ; 6}.

Définition :

  • Chaque éventualité est affectée d’une probabilité, c’est-à-dire d’un nombre noté pi tel que : 0 ≤ pi ≤ 1 et p1 + p2 + · · · + pn = 1
  • On appelle loi de probabilité la donnée des pi vérifiant ces conditions.
  • Si tous les événements élémentaires ont la même probabilité, on dit qu’ils sont équiprobables, ou que la loi de probabilité p est équiprobable.

Exemple : On lance un dé à 6 faces bien équilibré. Chaque face ayant les mêmes chances d’apparaître, chaque éventualité a une probabilité de

\frac{1}{6}
16\frac{1}{6}

La loi de probabilité est donc  :

1 2 3 4 5 6
\frac{1}{6}
16\frac{1}{6}
\frac{1}{6}
16\frac{1}{6}
\frac{1}{6}
16\frac{1}{6}
\frac{1}{6}
16\frac{1}{6}
\frac{1}{6}
16\frac{1}{6}
e_i
eie_i
p_i
pip_i
\frac{1}{6}.
16.\frac{1}{6}.

Remarque : De manière générale, si une expérience aléatoire est équiprobable et comporte n issues différentes, chacune des issues a une probabilité de \(\frac{1}{n} \)

1.2 Vocabulaire des événements

Définition :

Un événement A est une partie de l’univers Ω (on note A ⊂ Ω). 

∅ est l’événement impossible.

Ω est l’événement certain.

Exemple : On lance un dé à 6 faces bien équilibré. 

Des exemples d’événement :

A : « Obtenir un nombre pair » : A = {2 ; 4 ; 6}

B : « Obtenir un nombre inférieur ou égal à 2 » : B = {1 ; 2}

B’ : « Obtenir un nombre strictement supérieur à 4 » : B’ = {5 ; 6}

C : « Obtenir 7 » : C = ∅ (événement impossible)

D : « Obtenir un nombre inférieur ou égal à 6 » :

D = {1 ; 2 ; 3 ; 4 ; 5 ; 6} = Ω (événement certain)

Définition :

Soient A et B deux événements d’un univers Ω.

  • L’événement A∩B est l’événement « A et B ».
  • L’événement A∪B est l’événement « A ou B ».
  • L’événement      est l’événement « contraire de A » ou « non A ».
  • Deux événements A et B sont incompatibles s’ils ne peuvent pas se réaliser en même temps, c’est-à-dire si A ∩ B = ∅. 
\bar{A}
Aˉ\bar{A}

Exemple : On reprend les notations de l’exemple précédent.  

  • A ∩ B est l’événement « Obtenir un nombre pair inférieur ou égal à 2 ». A ∩ B = {2}
  • A ∪ B est l’événement « Obtenir un nombre pair ou un nombre inférieur ou égal à 2 ». A ∪ B = {1 ; 2 ; 4 ; 6}
  • \(\bar{A}\) est l’événement « Obtenir un nombre impair ». \(\bar{A}\)  = {1 ; 3 ; 5 }
  • Les événements B et B’ sont incompatibles.

1.3 Probabilité d'un événement

Propriété :

La probabilité d’un événement A est la somme des probabilités des issues qui le composent. On la note p (A).

On a donc 0 ≤ p (A) ≤ 1.

Remarques :

  • p (Ω) = 1 . L’ensemble Ω est un événement certain.
  • p (∅) = 0 . L’ensemble vide est un événement impossible.
  • Dans le cas de l’équiprobabilité, si l’univers Ω comporte n issues, on a :

Propriété :

  • Si A et B sont deux événements :

p (A ∪ B) = p (A) + p (B) − p (A ∩ B) et p (\(\bar{A}\)) = 1 − p (A)

  • Si les événements A et B sont incompatibles :

p (A ∪ B) = p (A) + p (B)

Exemple : On reprend les notations de l’exemple du 1.2 

On lance un dé à 6 faces bien équilibré. 

A : « Obtenir un nombre pair » : A = {2 ; 4 ; 6}

B : « Obtenir un nombre inférieur ou égal à 2 » : B = {1 ; 2}

  •  
  •  
  •  
p(A)=\frac{3}{6}=\frac{1}{2}\;et\;p(\bar{A})=1-\frac{1}{2}=\frac{1}{2}
p(A)=36=12  et  p(Aˉ)=1−12=12p(A)=\frac{3}{6}=\frac{1}{2}\;et\;p(\bar{A})=1-\frac{1}{2}=\frac{1}{2}
p(B)=\frac{2}{6}=\frac{1}{3}\;et\;p(A\cap B)=\frac{1}{6}
p(B)=26=13  et  p(A∩B)=16p(B)=\frac{2}{6}=\frac{1}{3}\;et\;p(A\cap B)=\frac{1}{6}
p(A \cup B)=\frac{1}{2}+\frac{1}{3}-\frac{1}{6}=\frac{4}{6}=\frac{2}{3}
p(A∪B)=12+13−16=46=23p(A \cup B)=\frac{1}{2}+\frac{1}{3}-\frac{1}{6}=\frac{4}{6}=\frac{2}{3}

2 Variable aléatoire

2.1 Un exemple pour comprendre

Exemple : On lance trois pièces de monnaie équilibrées.

L’univers est : Ω = {PPP ; PPF ; PFP ; FPP ; PFF ; FPF ; FFP ; FFF}.

On gagne 1 € chaque fois que F apparaît et on perd 1 € chaque fois que P apparaît. On note X la fonction qui, à chaque issue, associe le gain algébrique (positif ou négatif) correspondant.

X est appelée variable aléatoire sur Ω. Les valeurs possibles pour X sont {−3 ; −1 ; 1 ; 3} 

  • L’événement X = −3 est {PPP}. Sa probabilité est p (X = −3) =
\frac{1}{8}.
18.\frac{1}{8}.
  • L’événement X = −1 est {PPF ; PFP ; FPP}.

      Sa probabilité est p (X = −1) =

\frac{3}{8}.
38.\frac{3}{8}.
  • L’événement X = 1 est {FFP ; FPF ; FPP}.

      Sa probabilité est p (X = 1) =

\frac{3}{8}.
38.\frac{3}{8}.
  • L’événement X = 3 est {FFF}. Sa probabilité est p (X = 3) =
\frac{1}{8}.
18.\frac{1}{8}.

On résume ceci dans un tableau, appelé loi de probabilité de la variable aléatoire X :

-3 -1 1 3
\frac{1}{8}
18\frac{1}{8}
\frac{3}{8}
38\frac{3}{8}
\frac{3}{8}
38\frac{3}{8}
\frac{1}{8}
18\frac{1}{8}
gain\;x_i
gain  xigain\;x_i
p(X=x_i)
p(X=xi)p(X=x_i)

2.2 Loi de probabilité d’une variable aléatoire

Définition :  Soit Ω l’univers associé à une expérience aléatoire.

  • On appelle variable aléatoire X toute fonction définie sur Ω, à valeurs dans R.
  • On note x1 ; x2 ; . . . ; xn les valeurs prises par X. On appelle loi de probabilité de la variable aléatoire X la fonction qui, à chaque xi , associe la probabilité de l’événement p (X = xi). On peut résumer les résultats dans un tableau :

 

 

 

p_1
p1p_1
p_2
p2p_2
...
......
p_n
pnp_n
x_i
xix_i
p(X=x_i)
p(X=xi)p(X=x_i)
x_1
x1x_1
x_2
x2x_2
...
......
x_n
xnx_n
\sum_{i=1}^{n} p(X=x_i)=1
∑i=1np(X=xi)=1\sum_{i=1}^{n} p(X=x_i)=1

Remarque : 

On a 

3 Paramètres d'une variable aléatoire

3.1 Espérance, variance, écart-type

Définition :  Avec les notations précédentes, on appelle :

  • Espérance mathématique de X :

 

  • Variance de X :

 

 

 

  • Écart-type de X :

 

E(X)=p_1x_1+p_2x_2+...+p_nx_n=\sum_{i=1}^np_ix_i
E(X)=p1x1+p2x2+...+pnxn=∑i=1npixiE(X)=p_1x_1+p_2x_2+...+p_nx_n=\sum_{i=1}^np_ix_i
V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+...+p_n(x_n-E(X))^2
V(X)=p1(x1−E(X))2+p2(x2−E(X))2+...+pn(xn−E(X))2V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+...+p_n(x_n-E(X))^2
=\sum_{i=1}^np_i(x_i-E(X))^2
=∑i=1npi(xi−E(X))2=\sum_{i=1}^np_i(x_i-E(X))^2
\sigma=\sqrt{V(X)}
σ=V(X)\sigma=\sqrt{V(X)}
E(X)=(-3)\times \frac{1}{8}+(-1)\times \frac{3}{8}+1\times \frac{3}{8}+3\times \frac{1}{8}=0
E(X)=(−3)×18+(−1)×38+1×38+3×18=0E(X)=(-3)\times \frac{1}{8}+(-1)\times \frac{3}{8}+1\times \frac{3}{8}+3\times \frac{1}{8}=0
V(X)=\frac{1}{8}(-3-0)^2+\frac{3}{8}(-1-0)^2+\frac{3}{8}(1-0)^2+\frac{1}{8}(3-0)^2=\frac{24}{8}=3
V(X)=18(−3−0)2+38(−1−0)2+38(1−0)2+18(3−0)2=248=3V(X)=\frac{1}{8}(-3-0)^2+\frac{3}{8}(-1-0)^2+\frac{3}{8}(1-0)^2+\frac{1}{8}(3-0)^2=\frac{24}{8}=3
\sigma=\sqrt{3}\approx 1,732
σ=3≈1,732\sigma=\sqrt{3}\approx 1,732

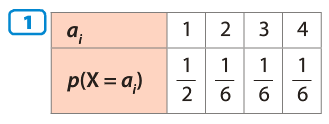
Exemples : On reprend l’exemple du 2.1 

-3 -1 1 3
\frac{1}{8}
18\frac{1}{8}
\frac{3}{8}
38\frac{3}{8}
\frac{3}{8}
38\frac{3}{8}
\frac{1}{8}
18\frac{1}{8}
gain\;x_i
gain  xigain\;x_i
p(X=x_i)
p(X=xi)p(X=x_i)

Remarques :

  • Pour obtenir l’espérance, on calcule la moyenne des valeurs xi pondérées par les probabilités pi.
  • La variance est la moyenne des carrés des écarts à l'espérance pondérés par les probabilités pi.

3.2 Jeu équitable

Définition :  

Ω est l’ensemble des issues d’un jeu de hasard.

X est la variable aléatoire définie sur Ω  qui donne le gain du joueur.

  • Dire que ce jeu est équitable signifie que E(X) = 0.
  • Si E (X) > 0, le jeu est favorable au joueur.
  • Si E (X) < 0, le jeu est défavorable au joueur. 

Exemples :

  • Dans l’exemple du 2.1 : E(X) = 0 donc ce jeu est équitable.
  • Dans le deuxième exemple du 3.1 : E(X) > 0 donc ce jeu est favorable au joueur.

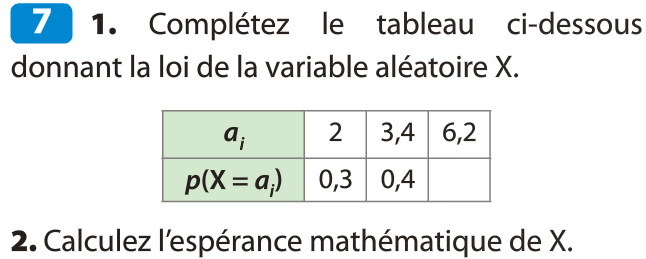
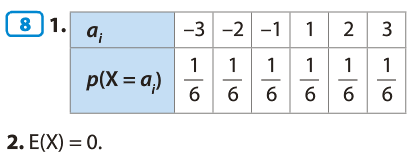
Exercices 1ES :

Made with Slides.com