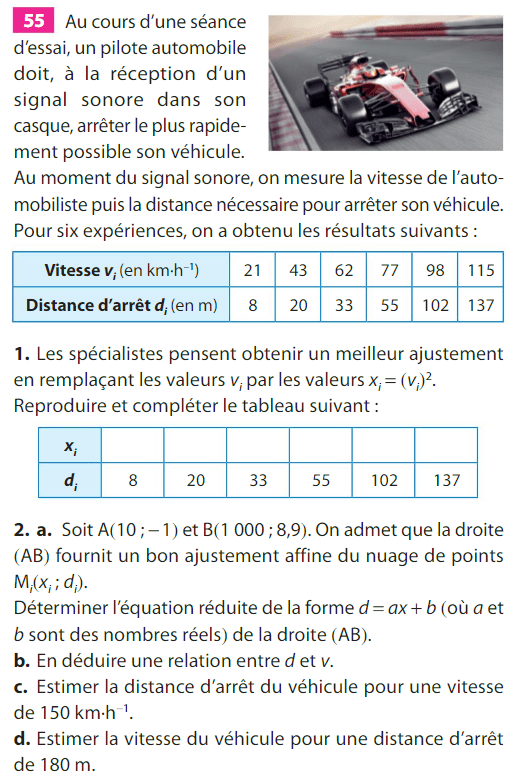
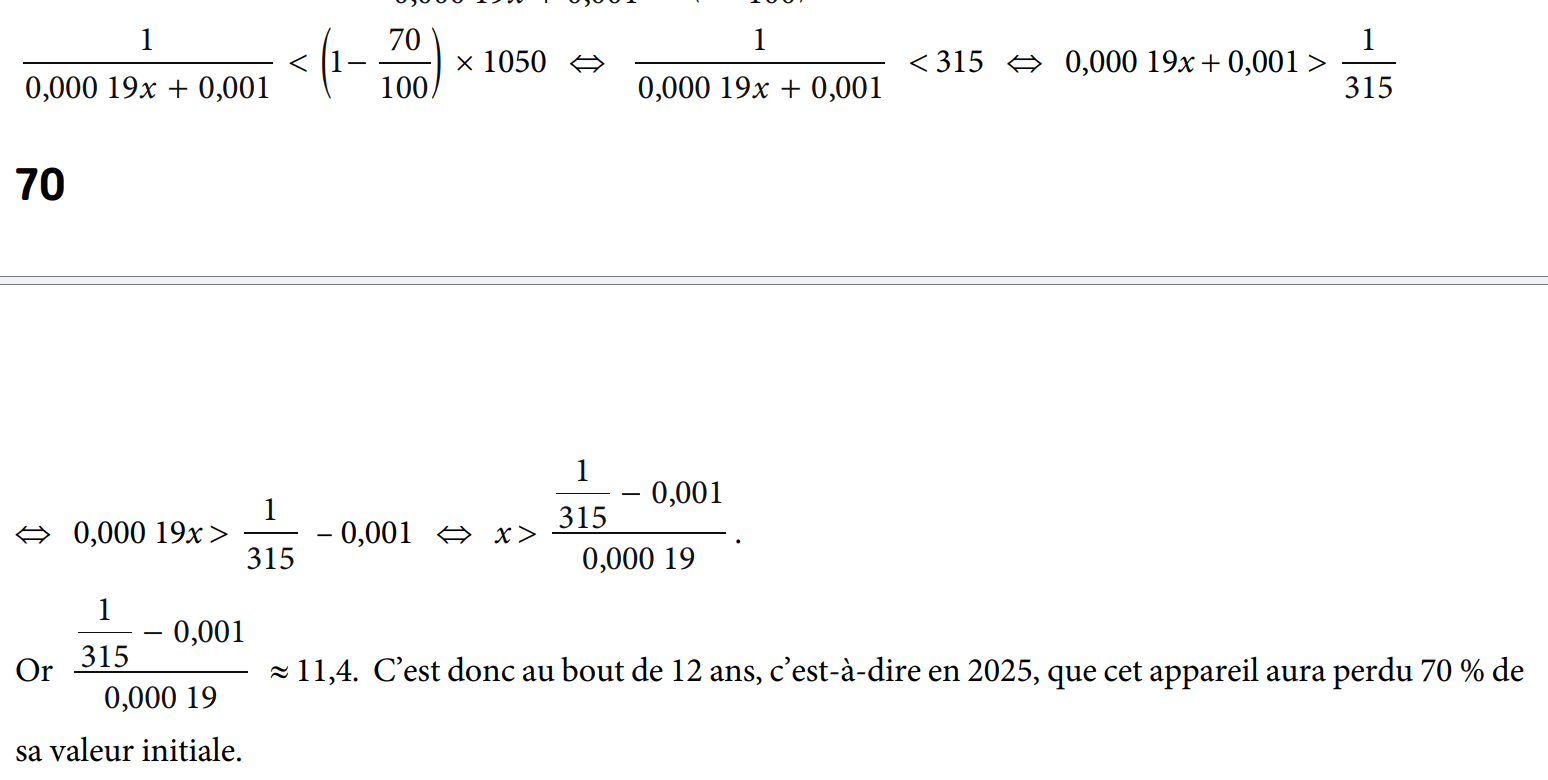Statistiques à deux variables





Lecture graphique :



Et quand \(a\) n'est pas un nombre entier...

?

?
Pour la lecture de \(b\), on lit l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées :





Exercice : Donner l'équation réduite des droites \(d_1\) à \(d_4\).
b) par le calcul
Par le calcul :

On veut calculer \(a\) et \(b\) dans
1) Calcul de \(a\) :
Exemple :

Donner l'équation réduite de la droite (AB).
2) Remplacer \(a\) par sa valeur dans l'équation :
3) Calcul de \(b\) : dans l'équation, on remplace \(x\) et \(y\) par les coordonnées de A ou de B :
3 = \(-2\) x 1 + b ou 7 = \(-2\) x (-1) + b
ce qui nous donne b = 5.
Conclusion : (AB) a pour équation :
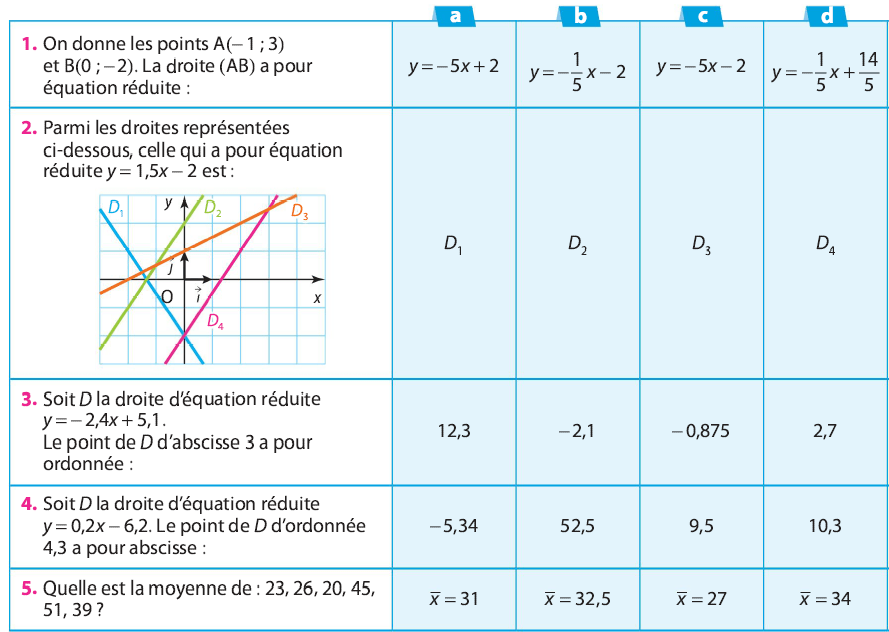

1. Les deux caractères étudiés sont la superficie des appartements et leur prix de vente.
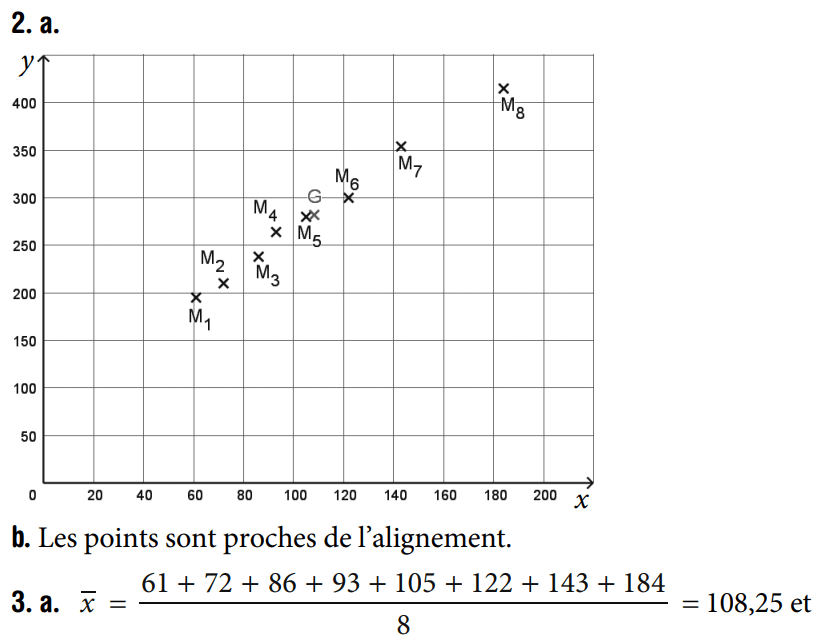




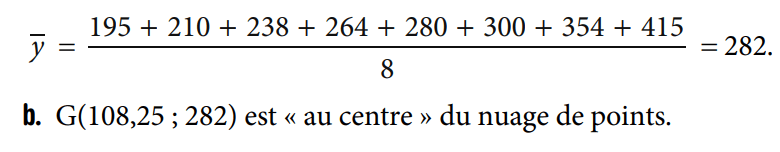
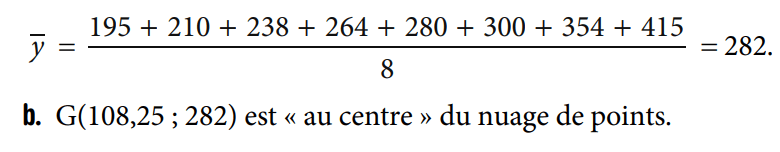

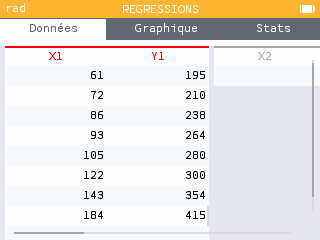
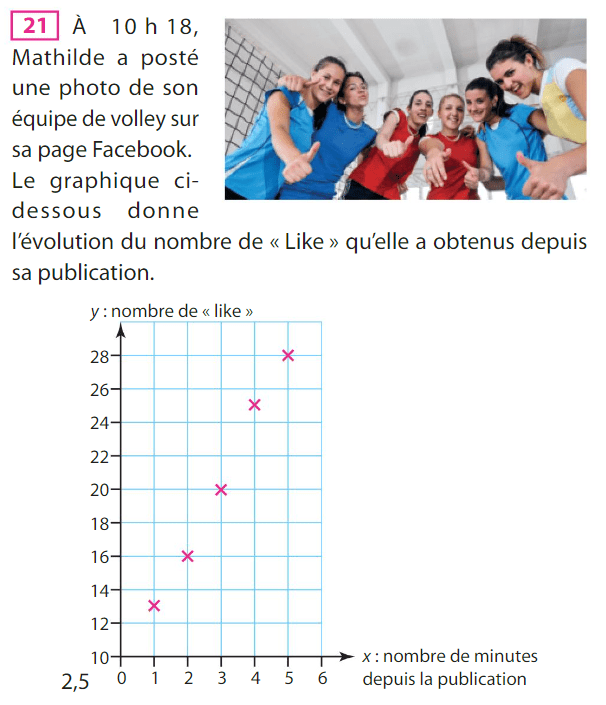




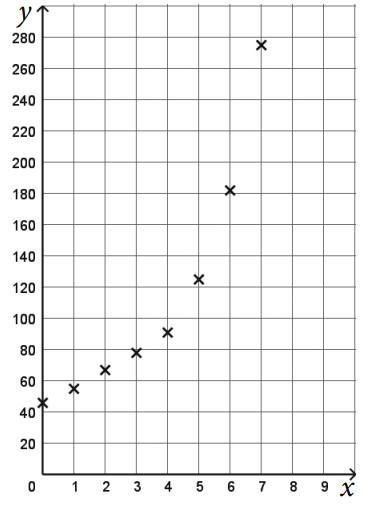
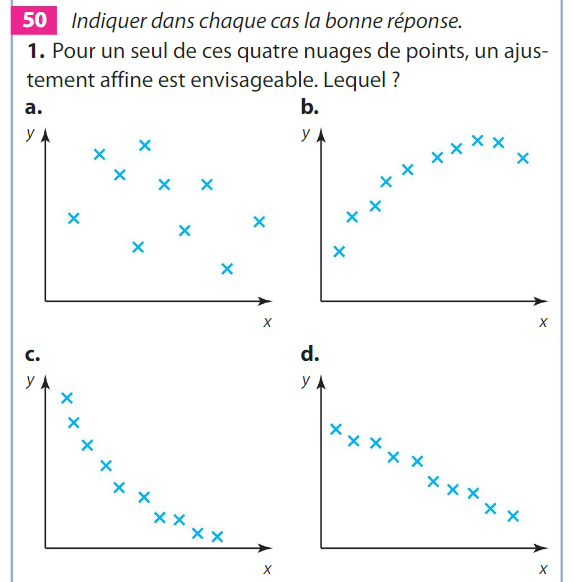
Les points ne sont pas proches de l'alignement donc un ajustement affine n'est pas envisageable.

Les points sont proches de l'alignement donc un ajustement affine est envisageable.
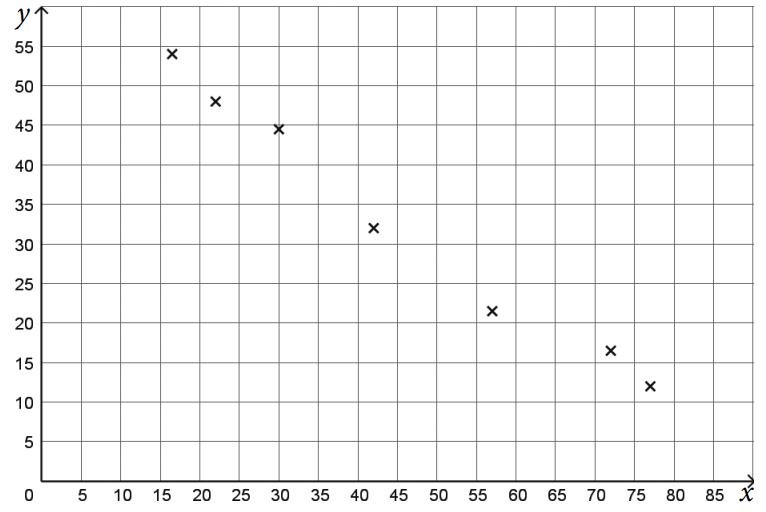

Les points ne sont pas proches de l'alignement donc un ajustement affine n'est pas envisageable.
Les points sont proches de l'alignement donc un ajustement affine est envisageable.
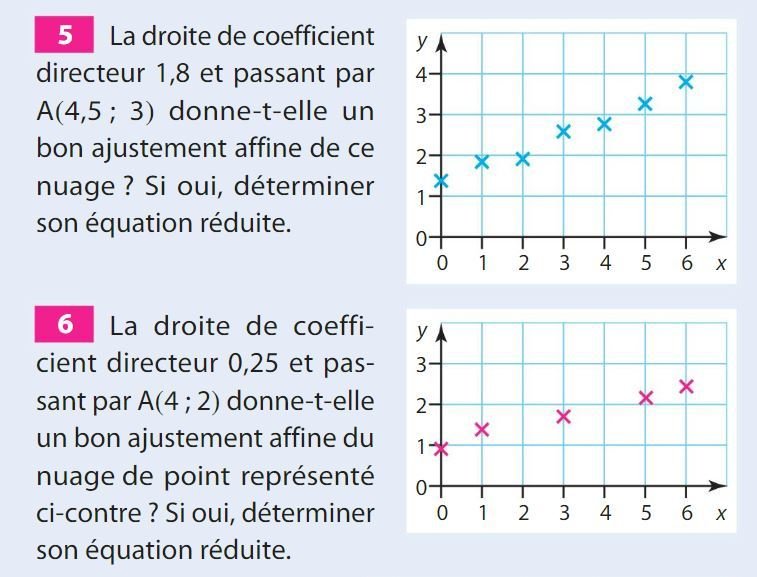
Non.

Oui.
Il faut déterminer l'équation de la droite :
Le coefficient directeur est 0,25 donc on cherche une équation de la forme : \(y=0,25x+b\)
Pour calculer \(b\) , on remplace \(x\) et \(y\) dans l'équation par les coordonnées de A :
Conclusion : la droite d'ajustement a pour équation \(y=0,25x+1\)
donc
d'où
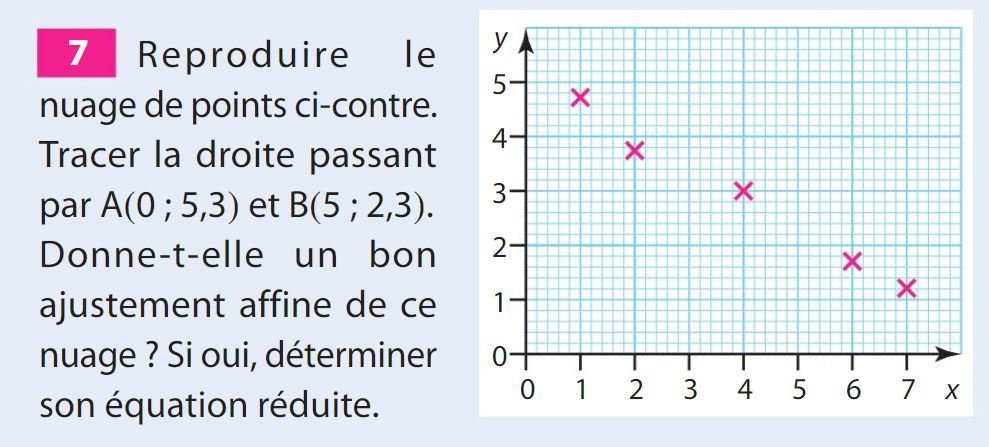
Oui.
Il faut déterminer l'équation de la droite :
La droite (AB) a une équation de la forme \(y=ax+b\)

Pour calculer \(b\) , on remplace \(x\) et \(y\) dans l'équation par les coordonnées de A :
Conclusion : la droite d'ajustement a pour équation \(y=-0,6x+5,3\)
donc
Le coefficient directeur est \(-0,6\) donc on cherche une équation de la forme : \(y=-0,6x+b\)
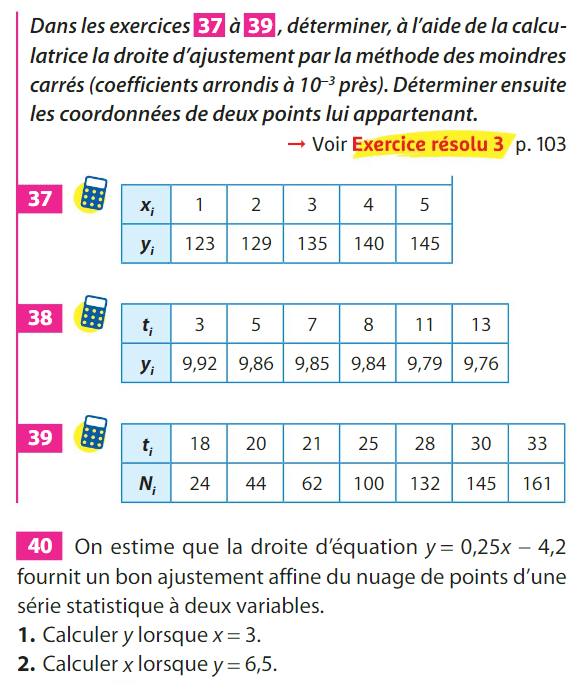
Faire un ajustement affine
Modéliser la tendance générale plutôt que les fluctuations.
Lorsque c'est pertinent, on cherche une droite qui représente au mieux la tendance du nuage (les données).
On ajuste une droite (un modèle affine y=ax+by=ax+by=ax+b) au nuage de points représentant les données (xi,yi)(x_i,y_i)(xi,yi).
Droite d'ajustement avec la méthode des moindres carrés


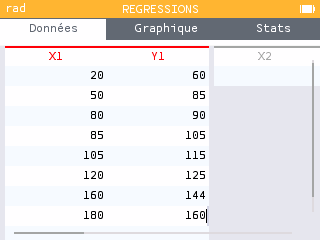
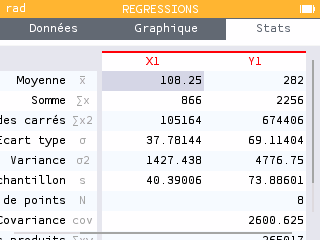
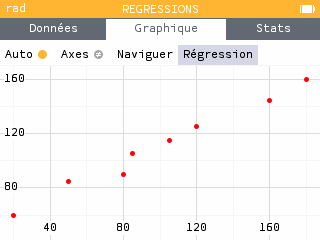
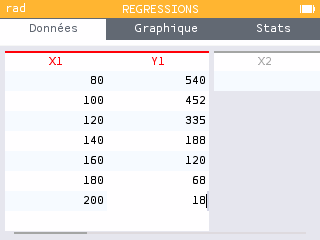
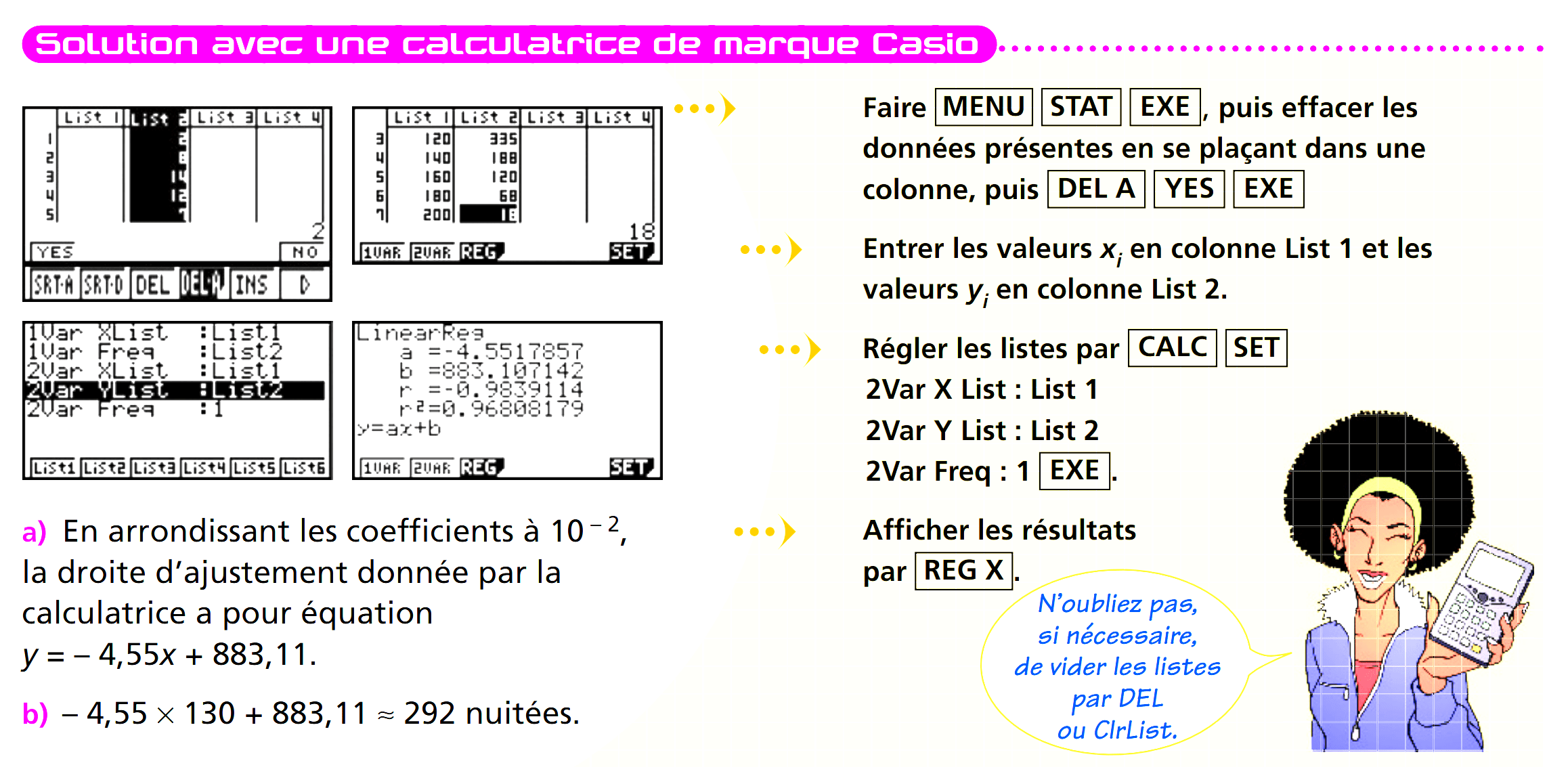
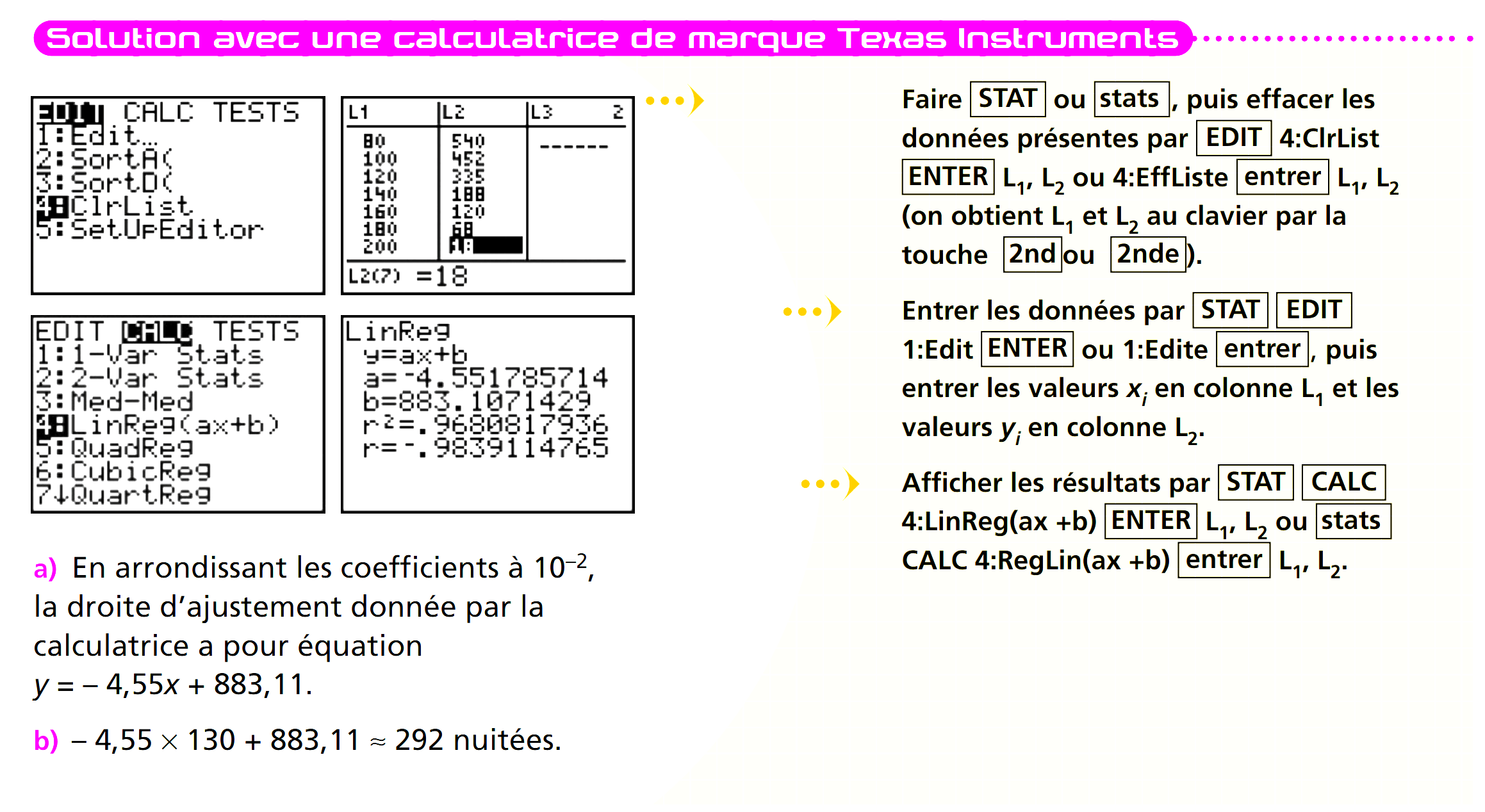
Aller dans le menu régression puis entrer les données.
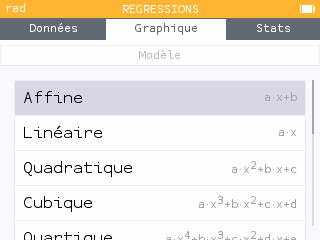
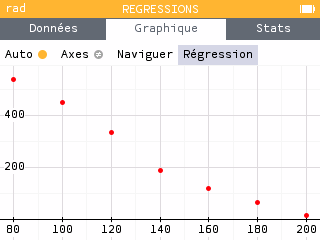
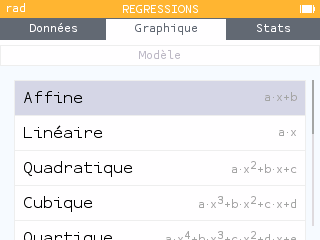
Aller dans l'onglet graphique puis dans l'onglet régression et choisir le modèle affine.
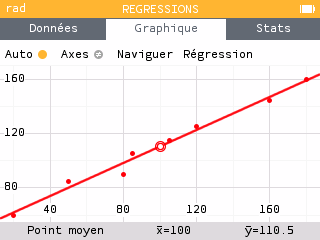
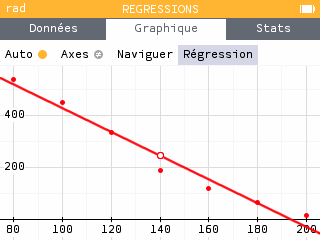
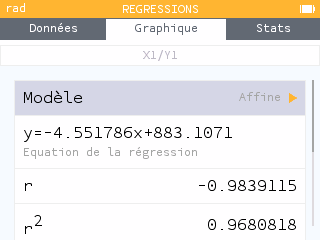
Retourner dans l'onglet régression pour avoir l'équation de la droite.
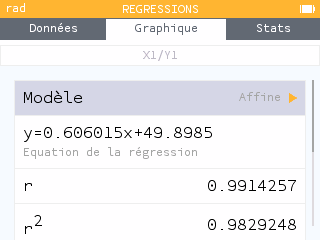
On demande souvent les coefficients a et b arrondis à 0,001 près.



Un peu d'histoire


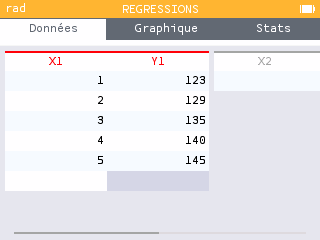
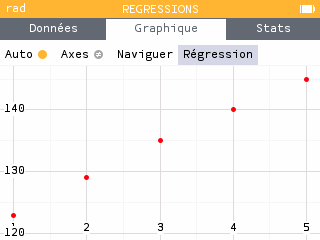
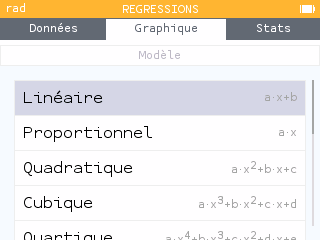
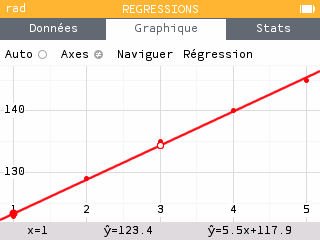
(cliquer vers le bas sur la croix multidirectionnelle)
ou affine
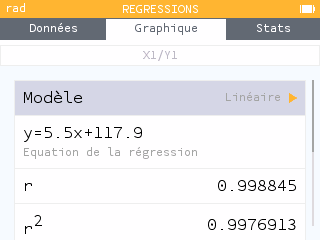
en cliquant à nouveau à nouveau sur régression





Donc pour un investissement en publicité de 3 000 €, le montant espéré du chiffre d’affaires est 76 100 €.
Donc pour un chiffre d’affaires de 84 240 €, l’investissement en publicité est estimé à 5 200 €.

Donc en 2021, le montant moyen des achats en ligne est estimé à 49,7 €.
C’est donc à partir de 2023 qu’on peut estimer que le montant des achats en ligne va devenir inférieur à 45 €.

Donc en 2025, le nombre de licences est estimé à 10260.
C’est donc à partir de 2023 qu’on peut estimer que le nombre des licences va devenir supérieur à 10000.
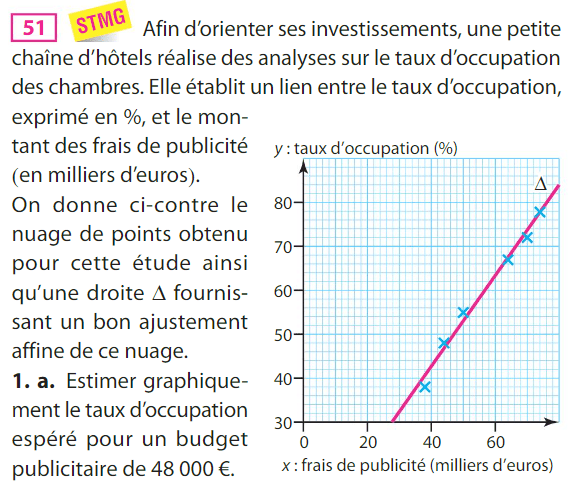

1. a. Le taux d’occupation espéré pour un budget publicitaire de 48 000 € est environ 51 %.
1. b. Le montant des frais publicitaires laissant espérer un taux d’occupation de 80 % est environ 76 000 €

• Pour \(x = 48\), on a \(y= 1,04 \times 48 + 0,56 = 50,48\).
Donc le taux d’occupation espéré pour un budget publicitaire de 48 000 € est 50,48 %.
• On résout l’équation \(1,04x + 0,56 = 80\)
\(1,04x = 79,44\)
\(x = \dfrac{79,44}{1,04}\)
\(\dfrac{79,44}{1,04}\approx 76,385\)
Donc le montant des frais publicitaires laissant espérer un taux d’occupation de 80 % est environ 76 385 €.