Estructuras Algebraicas
Juan Esteban Navarro C.
Conjuto
Operaciones
- Sumas
- Resta
- Multiplicación
- División
- Otros
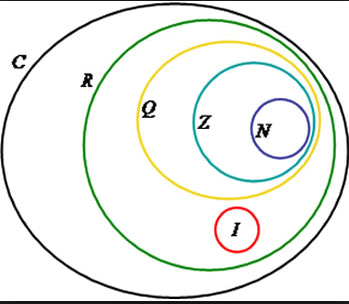
Conjuto
Conjuto



Leyes de Composición

MONOIDE

Propiedades que pueden cumplirse.

Por la izquierda y por la derecha.
Propiedades que pueden cumplirse.

Por la izquierda y por la derecha.
Grupo
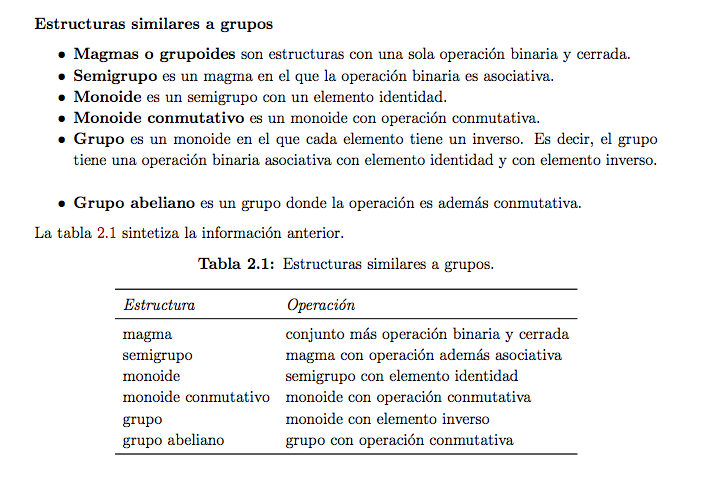
Grupo (AXIOMAS)
Sea (g,*) algún grupo. Si x,y,z pertenecen a g
x = y implica x*z = y*z
x = y implica z*x = z*y, ¿por qué?
Sea (g,*) algún grupo. Si w,x,y,z pertenecen a g
x = y, y además w=z entonces
x*w y w*x, = y*z y z*w ¿por qué?
Grupo (AXIOMAS)

Grupo (Teorema)
{ el inverso de:
(el inverso de:
( X )
) }= X
Grupo (Teorema)
{ el inverso de:
( x * y)
}= (el inverso de: x) * (el inverso de: y)
Grupo (Potencias)
(g,*) algún grupo, cuyo elemento neutro es e, para todo x que pertenezca a g y para todo n que pertenezca al conjunto de los números naturales {1,2,3,4,5,...,n}
Grupo (Teorema)
(g,*) alguna E.A y (h,*) otra E.A entnces.
Si * es comnmutativa en g, lo será en h.
Si * es asociativa en g, lo será en h.
Si e es el elemento neutro de g, lo será en h.
Subgrupo
