Learn to Relax:
Integrating Integer Linear
Programming with
Conflict-Driven Search

 

Jo Devriendt †*, Ambros Gleixner ‡, Jakob Nordström *†

 

Acknowledgement: Jan Elffers †*

† Lund University, Sweden

‡ Zuse Institut Berlin, Germany

* University of Copenhagen, Denmark

jodevriendt.com

Conflict-driven search for 0-1 ILP

an example-driven intro

+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1 \\
x,y,z,v,w \mapsto \{0,1\}

Conflict-Driven Search Loop

  • Input: 0-1 IL program
  • Output: either
    • solution
    • no solution exists
  • Search state:
    • set of constraints φ
    • partial assignment α
  • Initial state:
    • φ = input
    • α = {}

Conflict-Driven Search Loop

Unit propagation

  • Under α, if a constraint c ∈ φ would be falsified by assuming x=0 (resp. x=1), extend α with x=1 (resp. x=0)
  • Propagate until fixpoint

currently no unit propagation

\alpha=\{\}
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1

Unit propagation

Conflict?

\alpha=\{\}
  • Conflict: some c ∈ φ falsified by α
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

  • Only if unit propagation did not lead to a conflict
  • If no unassigned variable left, return solution
  • Resume unit propagation
\alpha=\{\}
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
\alpha=\{x=0\}
  • Only if unit propagation did not lead to a conflict
  • If no unassigned variable left, return solution
  • Resume unit propagation

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0\}
+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ +y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0\}
+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ +y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0,y=1\}
+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ +y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0,y=1\}
+1-z \geq 0 \\ -1+z-v \geq 0 \\ -z+2v-w \geq 0 \\ +1+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0,y=1,\\z=1,v=0\}
+1-z \geq 0 \\ -1+z-v \geq 0 \\ -z+2v-w \geq 0 \\ +1+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\ 0 \geq 0 \\ -1-w \geq 0 \\ +1+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Decide unassigned variable

no

\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\ 0 \geq 0 \\ -1-w \geq 0 \\ +1+w \geq 1
  • Conflict: some constraint in φ falsified by α

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Decide unassigned variable

yes

no

  • From falsified constraint and reasons, construct learned constraint
    • implied by φ, should prevent conflict
  • Add learned constraint to φ
    • → learned constraint database
\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\ 0 \geq 0 \\ -1-w \geq 0 \\ +1+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Decide unassigned variable

yes

no

\alpha=\{x=0,y=1,\\z=1,v=0\}
-2y+z-w \geq 0
  • From falsified constraint and reasons, construct learned constraint
    • implied by φ, should prevent conflict
  • Add learned constraint to φ
    • → learned constraint database
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
\textcolor{red}{2\times}
\textcolor{red}{1\times}
\textcolor{red}{+}

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

  • Backtrack based on learned constraint
  • Resume unit propagation
\alpha=\{x=0,y=1,\\z=1,v=0\}
-2y+z-w \geq 0
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1

Conflict-Driven Search Loop

  • Backtrack based on learned constraint
  • Resume unit propagation

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

  • Backtrack based on learned constraint
  • Resume unit propagation
\alpha=\{\}
-2y+z-w \geq 0
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

\alpha=\{\}
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
-2y+z-w \geq 0

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

-2y+z-w \geq 0
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
\alpha=\{y=0\}

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

+x-z \geq 0 \\ +z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+w \geq 1
+z-w \geq 0
\alpha=\{y=0\}

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

\alpha=\{y=0,w=1,\\x=0\}
-z \geq 0 \\ +z-v \geq 0 \\ -z+2v-1 \geq 0 \\ 1 \geq 1
+z-1 \geq 0

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

\alpha=\{y=0,w=1,\\x=0,z=0\}
0 \geq 0 \\ -v \geq 0 \\ +2v-1 \geq 0 \\ 1 \geq 1
-1 \geq 0

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

\alpha=\{y=0,w=1,\\x=0,z=0\}
0 \geq 0 \\ -v \geq 0 \\ +2v-1 \geq 0 \\ 1 \geq 1
-1 \geq 0

Conflict-Driven Search Loop

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

0 \geq 1
-2y+z-w \geq 0
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
\alpha=\{y=0,w=1,\\x=0,z=0\}

Conflict-Driven Search Loop

\textcolor{red}{+}
\textcolor{red}{+}

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

0 \geq 1

Unsatisfiable!

-2y+z-w \geq 0
+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1
\alpha=\{y=0,w=1,\\x=0,z=0\}

Conflict-Driven Search Loop

\textcolor{red}{+}
\textcolor{red}{+}

Unit propagation

Conflict?

Learn constraint

Backjump

Decide unassigned variable

yes

no

  • Learning constraints pushes search forward
  • Thousands of conflicts per second
  • Highly optimized unit propagation
  • Originates from Boolean satisfiability (SAT) [MS96,BS97,MMZZM01]
  • Generalized to pseudo-Boolean (PB) solving [CK05,SS06,LP10,EN18]
    • many variations possible

here be dragons

Conflict-Driven Search Loop

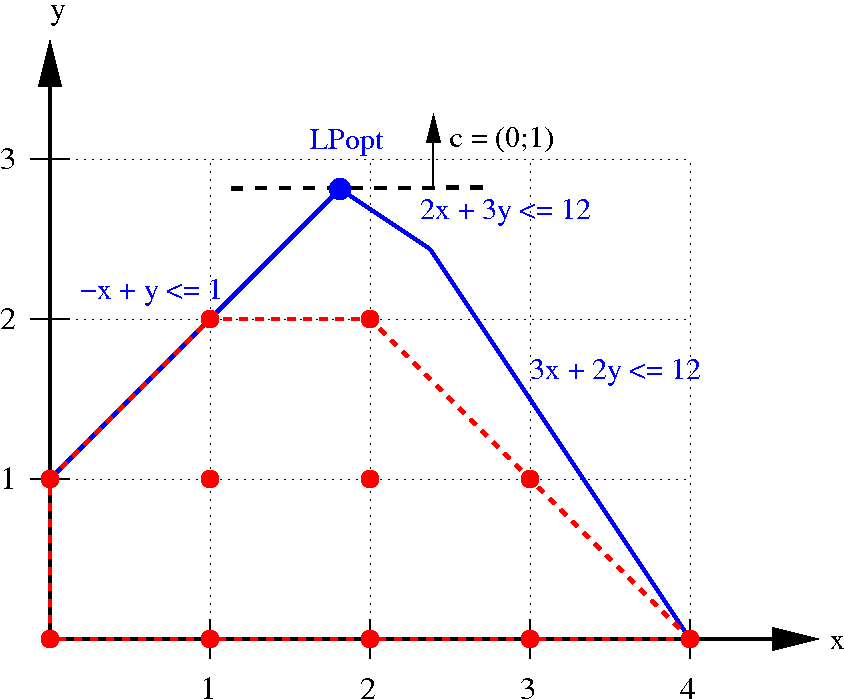
Another look at our example...

+x+y-z \geq 0 \\ -y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1 \\
x,y,z,v,w \mapsto \{0,1\}
  • It's rationally infeasible!
  • Could be solved without search
  • In theory: rationally infeasible programs are easy for conflict-driven PB search
  • In practice: PB solvers timeout on certain rationally infeasible programs [EGNV18]
    • unit propagation is local
    • wrong constraints are learned

How about integrating an LP solver?

our work

Linear Programming (LP) solver

  • Input:
    • LP relaxation of φ
    • variable bounds α
    • objective function
  • Output: either
    • optimal rational solution
    • Farkas multipliers
      • define a positive linear combination of constraints
        in φ, falsified by α

Conflict-Driven Search Loop

with LP solver call

Unit Propagation

Conflict?

Backjump

Decide unassigned variable

no

Rational infeasibility?

Query LP solver

yes

no

Learn constraint

Extract Farkas multipliers

yes

Learn Farkas constraint

Rational infeasibility example

\textcolor{red}{+a}+x+y-z \geq 0 \\ \textcolor{red}{+b}-y+z-v \geq 0 \\ -z+2v-w \geq 0 \\ -x+y+w \geq 1 \\ \textcolor{red}{+a-b \geq 0}
\alpha=\{a=0,b=0\}
\textcolor{red}{\times 1}\\ \textcolor{red}{\times 2}\\ \textcolor{red}{\times 1}\\ \textcolor{red}{\times 1}\\ \textcolor{red}{\times 0}\\
+a+2b\geq 1

Farkas multipliers

conflicting
Farkas constraint

  • LP solvers are slow compared to conflict-driven search loop
    • limit calls to LP solver
    • limit LP solver running time
    • deterministic measure: balance #conflicts in conflict-driven solver to #pivots in LP solver
  • LP solver uses inexact floating point arithmetic
    • learned constraint must be implied by φ
    • calculate Farkas constraint with exact arithmetic
    • verify Farkas constraint is still conflicting
    • post-process Farkas constraint to eliminate noise

Two technical hurdles

  • Every once in a while, run LP solver to completion at root
    • use (optimal) rational solution as value heuristic
    • generate Chvátal-Gomory (CG) cuts
      • add to both LP solver and learned constraint set
  • Generate "deep" Chvátal-Gomory cuts from internal search nodes
    • valid at root node, so safe to add as learned constraint
  • Add learned constraints as cuts to the LP solver

Further ideas

  • PB solver RoundingSat [EN18]
    • Strong ILP constraint learning
    • Performed well in past PB competitions
    • Linear optimization built on top of conflict-driven search loop
  • LP solver SoPlex [ZIB]
    • SCIP's native LP solver
    • State-of-the-art open source

Working implementation

  • #pivots/#conflicts ≤ 1
  • 128 bit precision to calculate CG cuts and Farkas constraints
  • Cut parallelism check
  • for decision instances, minimize sum of variables in SoPlex
  • for pure CNFs, deactivate LP techniques

Design choices

Compare state-of-the-art

  • RoundingSat
  • Sat4J
  • NaPS
  • SCIP
  • Gurobi
  • CPLEX

to implementations

  • RS+SPX
  • RS+SPX+GC
  • RS+SPX+GC+LC

Experiments!

[PBCOMP]

[PBCOMP]

[PBCOMP]

[PBCOMP]

[P04]

[P04]

[MIPLIB]

[MIPLIB]

[MIPLIB]

[MIPLIB]

Related work

  • Combined conflict analysis and LP solving in other solving paradigms:
    • SAT: LPSAT [WW00]
    • CP: LCG-Glucose [D16]
    • SMT: deciding linear arithmetic [Dd06]
    • MIP: SAT-style learning, e.g. SCIP [ABKW08]
  • Key differences of our approach:
    • run LP solver incrementally
      • not until completion
    • native conflict analysis on all linear constraints
      • exponentially stronger than clausal conflict analysis

Summary

Conflict-driven search for 0-1 ILPs

  • Generates cuts from search conflicts
  • Does not always find short refutations for rational infeasibility
  • Allows sound & efficient integration with LP solver
  • Is further improved by value heuristic & Gomory cut generation

Thanks for your attention!

Experiments approach best of both worlds

[MS96] GRASP - a new search algorithm for satisfiability - Marques-Silva, Sakallah

[BS97] Using CSP lookback techniques to solve real-world SAT instances - Bayardo, Schrag

[WW00] Combining Linear Programming and Satisability Solving for Resource Planning - Wolfman, Weld

[MMZZM01] Chaff: Engineering an efficient SAT solver - Moskewicz, Madigan, Zhao, Zhang, Malik

[P04] Where are the hard knapsack problems? - Pisinger

[CK05] A fast pseudo-Boolean constraint solver - Chai, Kuehlmann

[SS06] Pueblo: A hybrid pseudo-Boolean SAT solver - Sheini, Sakallah

[Dd06] A Fast Linear-Arithmetic Solver for DPLL(T) - Dutertre, de Moura

[ABKW08] Constraint Integer Programming: A New Approach to Integrate CP and MIP - Achterberg, Berthold, Koch, Wolter

[LP10] The Sat4j library, release 2.2 - Le Berre, Parrain

[D16] Scheduling and rostering with learning constraint solvers - Downing

[EN18] Divide and conquer: Towards faster pseudo-boolean solving - Elffers, Nordström

[EGNV18] Using Combinatorial Benchmarks to Probe the Reasoning Power of pseudo-Boolean Solvers - Elffers, Giráldez-Cru, Nordström, Vinyals

[ZIB] SoPlex - soplex.zib.de

[PBCOMP] Latest PB competition - www.cril.univ-artois.fr/PB16/

[MIPLIB] The Mixed Integer Programming Library - miplib.zib.de

References