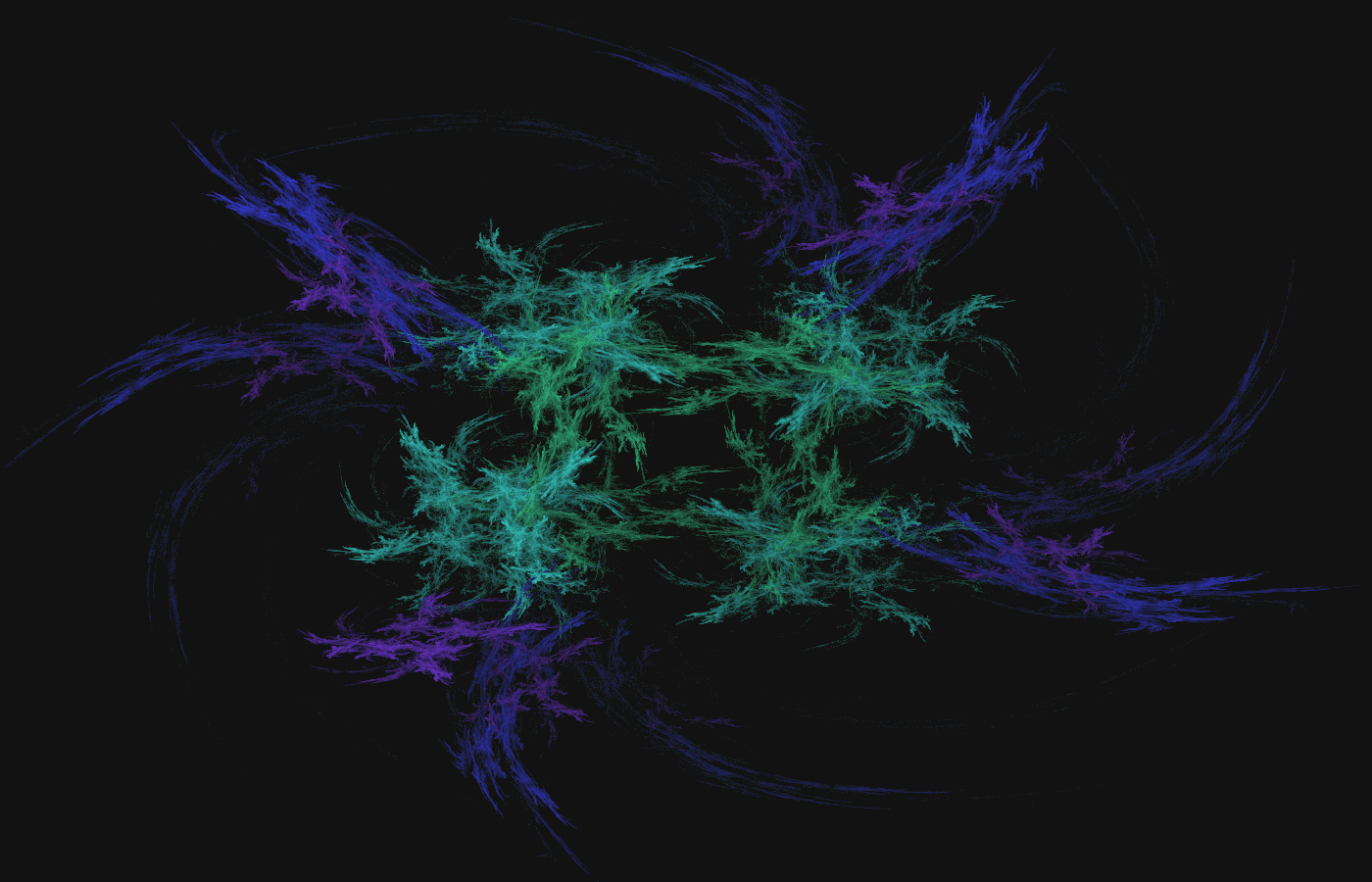
The Fractal Flame

Beauty out of Chaos

Johan Karlsson

  • Software developer
  • I've been coding since the 90's
  • JavaScript and Web since 2013
  • Patterns, algorithms, animations, fractals
  • Dwitter
  • Shadertoy
  • CodePen

Creative Coding

  • Creating freely
  • No requirements
  • Expression
  • Instant feedback
  • Generative / algorithmic art

Why?

  • Math and algorithms instead
    of textboxes over data
  • Exploring
  • The human machine cooperation
  • Being surprised
  • Relaxing

Mandelbrot Set

{\displaystyle f_{c}(z)=z^{2}+c}

A Fractal

  • Math...
  • Self-similar
  • Benoît Mandelbrot

beautiful, damn hard, increasingly useful. That's fractals.
- Benoît Mandelbrot

​

Julia Set

Koch Curve

A Fractal Flame

Affine Transformation

f(x, y) = (ax + by + c, dx + ey + f)
(1x + 0y + 0, 0x + 1y + 0) = (x, y)
(1x + 0y + 1, 0x + 1y + 1) = (x + 1, y + 1)

Affine Transform

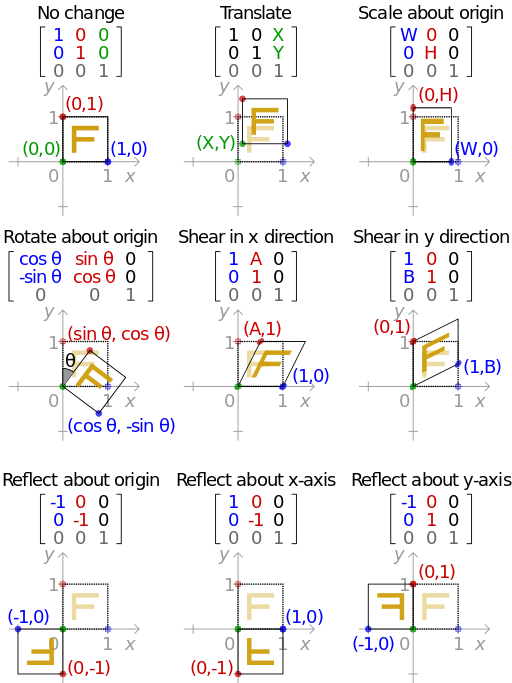
(Wikipedia) "2D affine transformation matrix" by Cmglee - Own work. Licensed under CC BY-SA 3.0 via Commons

 

IFS - Iterated Function System

  • A type of fractal
  • Several transformations
  • The Chaos Game algorithm
    is a common way to compute
    (draw) an IFS fractal

The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). - Wikipedia

Sierpinski Triangle - IFS

HSL (HSB)

Adobe Color

The Chaos Game

  • Create n affine transformations, f1-fn
  • Pick a random point (x, y)
  • Loop:
    • Apply a random affine transformation to get a new point: (xk+1, yk+1) = fr(xk, yk)
    • Plot the new point

Barnsley

Fern

A probability is assigned

to each transformation

Remember

f(x, y) = (ax + by + c, dx + ey + f)

Random IFS

Randomized:

  • Number of transformations
  • Each coefficient in each transformation
  • The color of each transformation

The Fractal Flame

  • Scott Draves

  • Based on the Chaos Game plus:

    • In addition to affine transformations you choose a non-linear function

    • Each affine transformation gets a color associated

    • Using log-density display - a histogram is updated instead of plotting directly 

Non-linear functions

Swirl

V_3(x, y) = x\sin(r^2) - y\cos(r^2), x\cos(r^2) + y\sin(r^2)
r = \sqrt {x^2 + y^2}
V_{42}(x, y) = (\frac{\sin x}{\cos y},\tan y)

Tangent

V_{27}(x, y) = \frac{2}{(r + 1)}(x, y)

Eyefish

The Fractal Flame Algorithm

  • User picks a non-linear function

  • Create n affine transformations, f1-fn

  • Create empty histogram h[width][height]

  • Pick a random point (x, y)

The Fractal Flame Algorithm (cont.)

  • Loop (millions of iterations)

    • Apply a random affine transformation OR non-linear function to get a new point: (xk+1, yk+1) = fr(xk, yk)

    • Update histogram color and frequency h[x][y]
      h[x][y][color] = (h[x][y][color] + colorr) / 2
      h[x][y][frequency]++

  • Draw histogram

    • h[x][y][color]
      alpha = log(h[x][y][frequency]) / log(frequencymax)

Demo

More info

References

Made with Slides.com