BETS - Desenvolvimento do pacote estatístico para extração e análise de séries temporais econômicas

Trabalho de Conclusão de Curso

Jonatha Azevedo da Costa

Orientador: Prof. Dr. Jony Arrais 

Motivação/Introdução

  1. Necessidade de dados
  2. Fontes não unificadas
  3. Encapsulamento de metainformações
  4. Não integração com ferramentas de análise

Imagine a situação de um economista obter dados pra uma análise de previsão para dados temporais de algum cenário econômico.

Dados

Atualizados

Poucos recursos computacionais e financeiros disponíveis

Meios para realizar a previsão

Diferentes fontes

Linguagem de programação livre

Brazilian Economic Time Series

Com alguma metodologia bem definida

  • RBCB
  • ecoseries
  • ribge
Pacotes Metadados Extação Exportração Análise
rbcb OK OK X X
ecoseries X OK X X
ribge X OK X X
BETS OK OK OK OK

O BETS não está sozinho no que diz respeito a obtenção de dados de forma integrada ao R , existem os pacotes: rbcb , ecoseries e o ribge .

O BETS é um pacote para o R , que fornece de maneira descomplicada , milhares de dados de diferentes fontes. Para utilizar, basta rodar o seguinte comando:

Para usar, basta:

install.packages("BETS")
require(BETS)

Imagem: Alguns centros de informações disponíveis. 

BETSsources()
The sources available at BETS, to date, are: 
 >  Banco Central, IBGE, Sidra, FGV

Objetivos

Apresentar minha participação no desenvolvimento do pacote BETS

Como é criado um pacote para o R

Processo de criação do pacote BETS

Algumas das funcionalidades do BETS

Forma de aplicação

Metodologia

Criação de pacotes para o R

Séries temporais

Box & Jenkins

Criação de pacotes no R

Vignettes

data

R

man

inst

src

LICENSE

DESCRIPTION

NAMESPACE

PKG

Tutoriais de uso

Arquivos de dados 

Códigos dos algoritmos

Documentação

Arquivos em gerais 

Códigos compilados 

Condições de uso

Informações gerais

Referenciamento nominal das funções

Criação de pacotes no R

Um exemplo de criação de um pacote para o R

function.R

Parte de documentação

#' Media
#' @param x um vetor de numeros
#' @return um valor numerico 
#' @importFrom Base message
#' @export 
#'
#' @examples
#' x = c(1,2,3,4,5,6)
#' media(x)

Parte do código

media <- function(x){
   if(!is.vector(x))stop("O parametro precisa 
    ser um vetor")
   message('Done!')
   return(sum(x,na.rm = T) / length(x))
  }

NAMESPACE

export(pkg,medida)
import(base,message)

Description

R

MAN

pacote.zip

No BETS ....

Função que se conecta no banco de dados

connection = function(){
    
    key <- readRDS(paste0(system.file(package="BETS"),"/key.rds"))
    dat <- readBin(paste0(system.file(package="BETS"),"/credentials.txt"),"raw",n=1000)
    aes <- AES(key,mode="ECB")
    raw <- aes$decrypt(dat, raw=TRUE)
    txt <- rawToChar(raw[raw>0])
    credentials <- read.csv(text=txt, stringsAsFactors = F)
    rm(key)

    conn = tryCatch({
        dbConnect(MySQL(),db=credentials$bd,user=credentials$login,
            password=as.character(credentials$password),
            host=credentials$host,
            port=credentials$port)

    }, error = function(e){
        return(NULL)
    })
    
    return(conn)
}

Séries temporais

Série temporal: Coleção de observações feitas sequencialmente ao longo do tempo.

Z_{t} = T_{t} + C_{t} + R_{t}.
Zt=Tt+Ct+Rt.Z_{t} = T_{t} + C_{t} + R_{t}.

(1)

  • Tendência: indica uma mudança de longo prazo no nível médio de uma série temporal;
  • Sazonalidade: está ligado à periodicidade ou ciclo geralmente em função de algum fenômeno dentro de um ano;
  • Erro: ruido branco, variável aleatória com média 0 e variância constante.

 

Box & Jenkins

A metodologia de Box & jenkins, consiste num processo de 5 passos:

  1. Considera-se uma classe geral de modelos: SARIMA(p,d,q)(P,D,Q);
  2. Identifica-se um modelo com base nas autocorrelações e autocorrelações parciais e outros critérios;
  3. Estima-se os parâmetros do modelo identificado;
  4. Verifica-se se o modelo ajustado é adequado aos dados através de uma análise de resíduos;
  5. Repete-se os passos anteriores até obter resultados coerentes.

Estudo de Caso

Motivação/Contexto

Quero fazer uma análise dos dados da Produção Física Industrial  do Brasil. 

Desejo realizar previsões (forecasting) dos dados para meses a frente!

A pesquisa Industrial Mensal da Produção Física - Brasil tem como objetivos:

Servir como medida da evolução de curto prazo do valor adicionado da indústria, dado um determinado período de referência;

Refletir rapidamente a trajetória da atividade fabril no curto prazo;

Importante dado de insumo para o PIB (Produto Interno Bruto).

Preliminares e Identificação


metadados_pim = BETS::sidraSearch(description = 'Producao fisica',view = F)
View(metadados_pim)


data <-  BETS::sidraGet(x = c(3653), from = c("200201"), to = c("201710"), 
    territory = "brazil",variable = 3135, sections = c(129316), cl = 544)

data <- ts(data$serie_3653$Valor,start = c(2002,01),frequency = 12)

Identificando e obtendo os dados

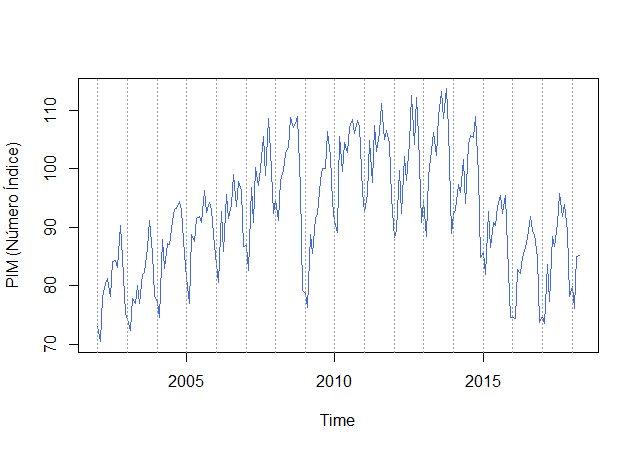
Imagem: Gráfico da produção física industrial

Algumas características observadas:

  • Sazonalidade;
  • Regularidade;
  • Quebra estrutural que afeta a tendência.

 

Teste para Estacionariedade

Def: uma série                             se diz   estacionária se e somente se:

Z = \{Z_{t}, t \in T\}
Z={Zt,t∈T}Z = \{Z_{t}, t \in T\}
E\{Z(t)\} = \mu(t) = \mu
E{Z(t)}=μ(t)=μE\{Z(t)\} = \mu(t) = \mu
t \in T
t∈T t \in T

, para todo

E\{Z^{2}(t)\}
E{Z2(t)}E\{Z^{2}(t)\}
t \in T
t∈T t \in T

, para todo

\gamma(t_{1},t_{2}) = Cov\{Z(t_{1},Z(t_{2}))\}
γ(t1,t2)=Cov{Z(t1,Z(t2))}\gamma(t_{1},t_{2}) = Cov\{Z(t_{1},Z(t_{2}))\}

, é uma função de 

\| t_{1} - t_{2}\|
∥t1−t2∥\| t_{1} - t_{2}\|

(2)

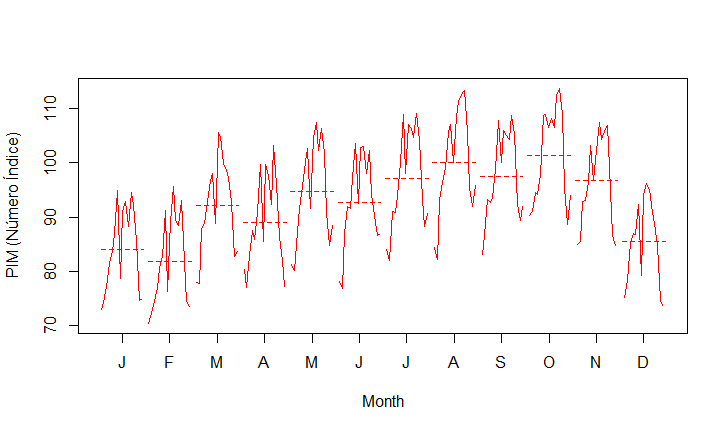
Imagem: Gráfico mensal da produção física industrial

Utilizando o teste ADF (Augmented Dickey Fuller)

Implementado de um forma diferente pelo BETS:

df = BETS::ur_test(y = diff(data), type = "drift",
 lags = 11, selectlags = "BIC", level = "1pct")
df$results
statistic crit.val rej.H0
tau2 -3.565171 -3.46 yes
phil1 6.363551 6.52 yes 
df = BETS::ur_test(y = diff(data),
 type = "drift", lags = 11,
 selectlags = "BIC", level = "1pct")

df$results
statistic crit.val rej.H0
tau2 -2.743174 -3.46 no
phil1 3.772285 6.52 yes

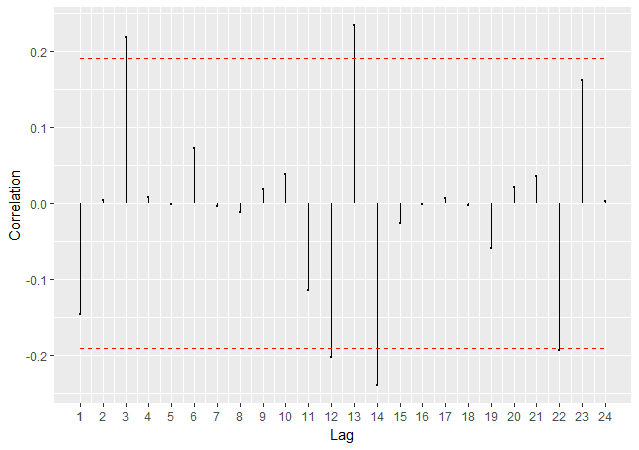
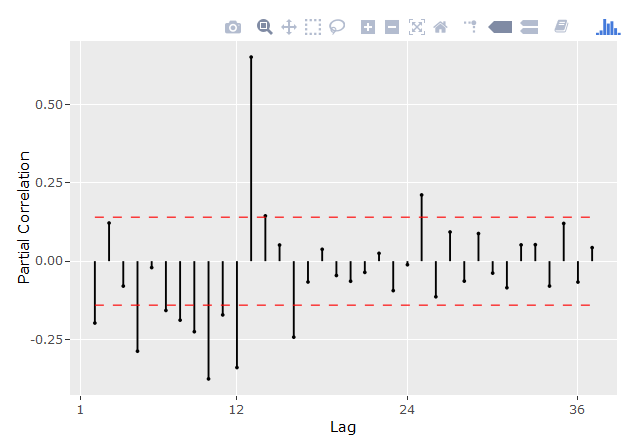
Imagem: Gráfico da autocorrelação

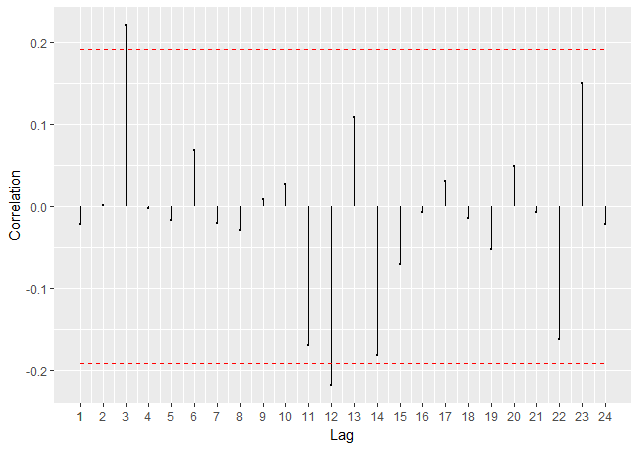
FAC 

FAC P

BETS::corrgram(diff(data), lag.max = 36,
 type = "normal", style="normal")
BETS::corrgram(diff(data), lag.max = 36, 
type = "partial", style="normal")
(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta(1 - \Phi_{1}B^{12})\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}.
(1−ϕ1B−ϕ2B2−ϕ3B3)Δ(1−Φ1B12)Δ12Xt=(1+θ1B+θ2B2)(1+Θ1B12)et. (1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta(1 - \Phi_{1}B^{12})\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}.

SARIMA(3,2,2)(1,1,1)[12]

Imagem: Gráfico da autocorrelação dos dados diferenciados

Imagem: Gráfico da autocorrelação parcial dos dados diferenciados

Estimação

modelo = Arima(data,order= c(3,2,2),seasonal = c(1,1,1))

Series: data 
ARIMA(3,1,2)(0,1,1)[12] 

Coefficients:
          ar1      ar2      ar3     ma1     ma2     sma1
      -1.5022  -1.3937  -0.3404  1.1901  0.9999  -0.8152
s.e.   0.0775   0.0884   0.0764  0.0262  0.0264   0.0678

sigma^2 estimated as 7.41:  log likelihood=-451.77
AIC=917.55   AICc=918.18   BIC=940.05
# Teste t com os coeficientes estimados
# Nivel de significancia de 1%

BETS::t_test(modelo, alpha = 0.01)


            Coeffs Std.Errors        t Crit.Values Rej.H0
ar1  -0.5923042 0.19130484 3.096127    2.602376   TRUE
ar2  -0.1927980 0.12575791 1.533089    2.602376  FALSE
ar3   0.2551995 0.09151118 2.788725    2.602376   TRUE
ma1  -0.7913874 0.19428788 4.073272    2.602376   TRUE
ma2  -0.2082854 0.19275454 1.080573    2.602376  FALSE
sar1  0.1397710 0.10747793 1.300462    2.602376  FALSE
sma1 -0.8954013 0.11062226 8.094224    2.602376   TRUE

SARIMA(3,1,2)(0,1,1)[12]

(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}.
(1−ϕ1B−ϕ2B2−ϕ3B3)ΔΔ12Xt=(1+θ1B+θ2B2)(1+Θ1B12)et.(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}.

Testes de Diagnóstico

x = (modelo$residuals - mean(modelo$residuals))/sd(modelo$residuals)
round(x)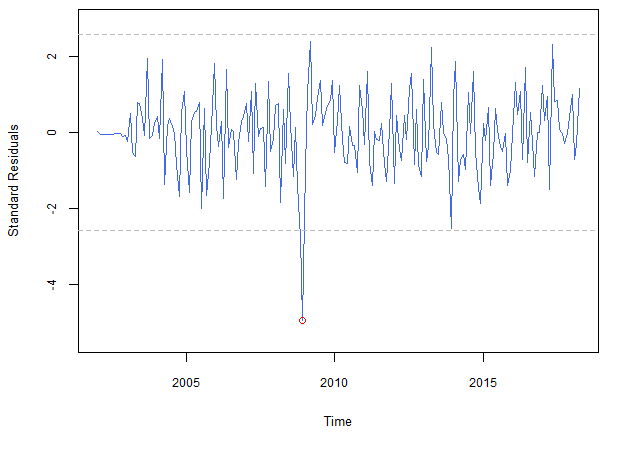
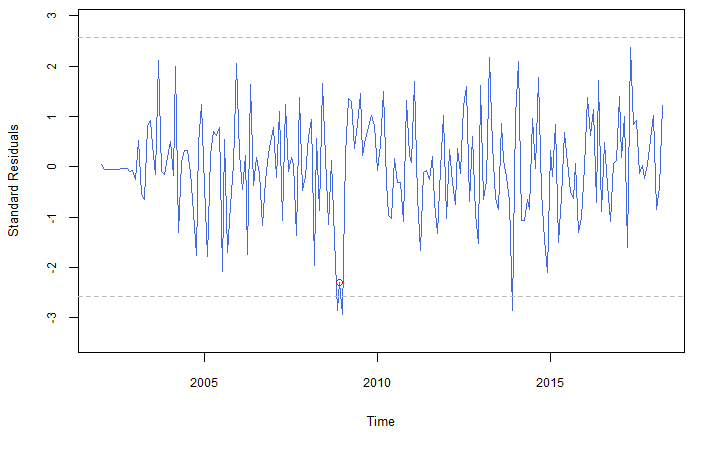
D_{t} = \begin{cases} & 1 \text{, } \text{dezembro de 2008} = t \\ & 0 \text{, } t < \text{caso contrário} \end{cases}
Dt={1, dezembro de 2008=t0, t&lt;caso contraˊrioD_{t} = \begin{cases} &amp; 1 \text{, } \text{dezembro de 2008} = t \\ &amp; 0 \text{, } t &lt; \text{caso contrário} \end{cases}
(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t} + \beta D_{t}
(1−ϕ1B−ϕ2B2−ϕ3B3)ΔΔ12Xt=(1+θ1B+θ2B2)(1+Θ1B12)et+βDt(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t} + \beta D_{t}
dummy <-  BETS::dummy(start = c(2002,01),end = c(2018,04),month =12 ,
year = 2008 ,frequency = 12)

Imagem: Gráfico dos resíduos do modelo

Imagem: Gráfico dos resíduos do modelo com a v.a. dummy

Utilizando o teste de Ljung-Box


boxt = Box.test(resid(modelo2), type = "Ljung-Box",lag = 11)

Box-Ljung test
data:  resid(modelo2)
X-squared = 3.0492, df = 11, p-value = 0.9901

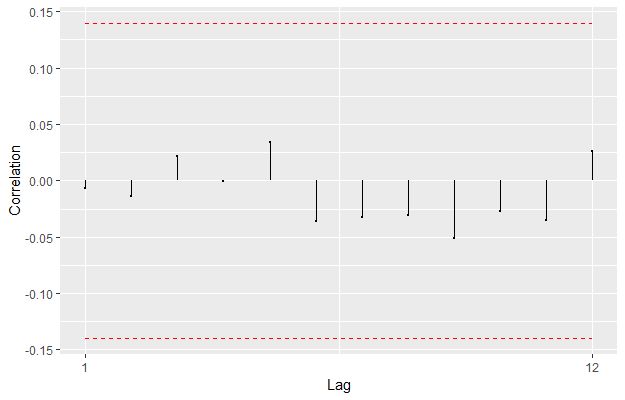
Imagem: Gráfico da autocorrelação dos resíduos do modelo com a dummy

Previsão

Previsão mês a mês, ou seja 1 passo, sucessivamente, a frente de janeiro até a outubro de 2017;

Previsão, 9 passos a frente, de uma vez só.

Jan - Out/17

Jan/2002 - Dez/2016

Amostra

Previsão

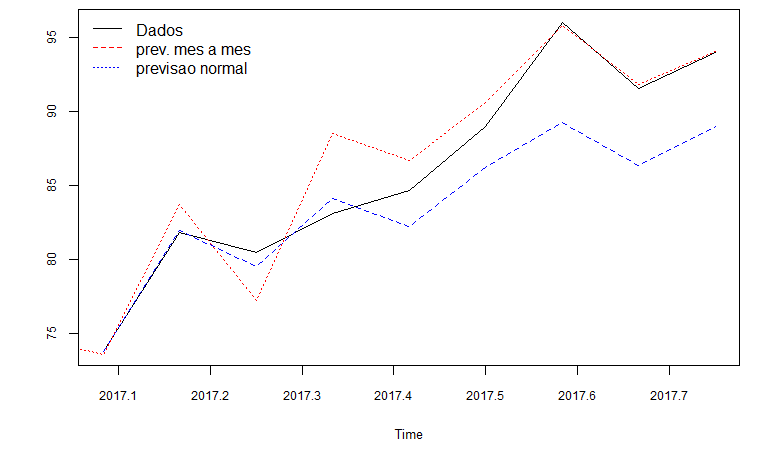
Imagem: Gráfico das previsões

Conclusão e Resultados

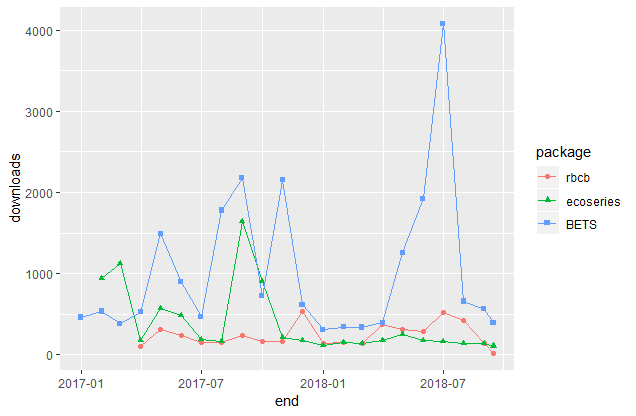
Imagem: Número de download dos pacotes ao longo do tempo

O que será construído a seguir, é: 

 

  •  Versões futuras do pacote. Novas funcionalidades:
    • Funções para dados de expectativas do mercado
      • Inflação acumulada 12 meses a frente
      • Taxa Over-Selic
      • Mais dados livres da FGV
    • Funções para dados governamentais

OBRIGADO!

Made with Slides.com