PIM-PF

Produção Física Industrial

ANÁLISE DE SÉRIES TEMPORAIS

Trabalho final

(2012 = 100)

SUMÁRIO

INTRODUÇÃO

A SÉRIE TEMPORAL

ESTIMAÇÃO DO MODELO

PREVISÃO

CONCLUSÃO

ANÁLISE EXPLORATÓRIA

INTRODUÇÃO

A pesquisa Industrial Mensal da Produção Física - Brasil tem como objetivos:

  • Servir como medida da evolução de curto prazo do valor adicionado da indústria, dado um determinado período de referência.
  • Refletir rapidamente a trajetória da atividade fabril no curto prazo;
  • Importante dado de insumo para o PIB (Produto Interno Bruto)

A SÉRIE TEMPORAL

Pegando os dados com o BETS

dados <-  BETS.sidra.get(x = c(3653), from = c("200201"), to = c("201710"),
 territory = "brazil",variable = 3135, sections = c(129316), cl = 544)

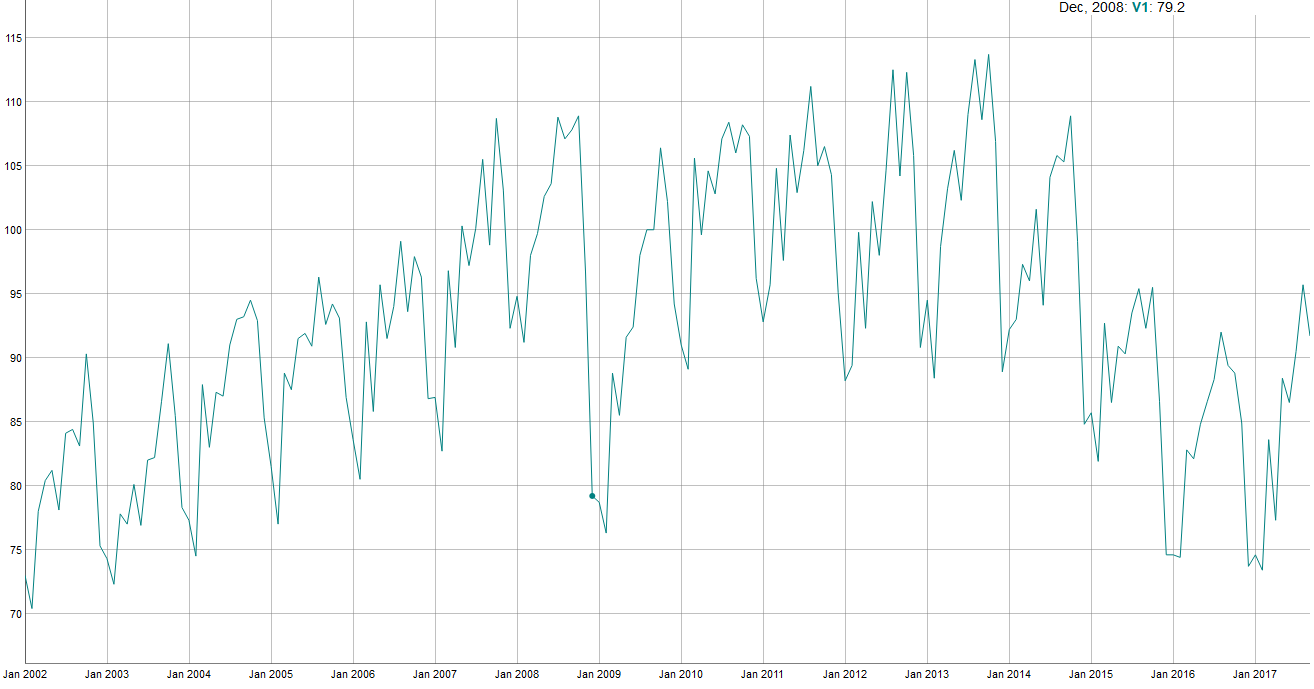
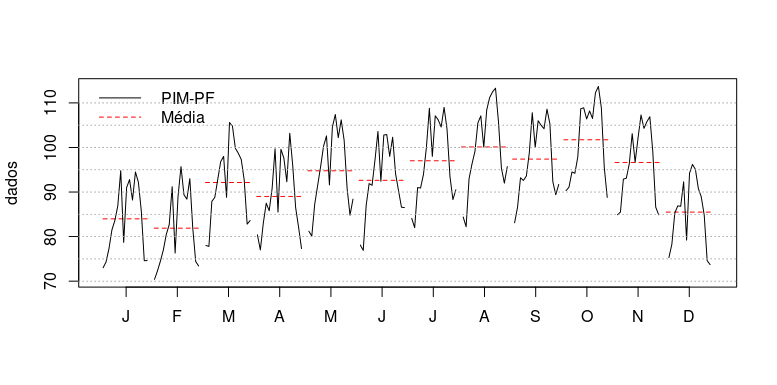
Série histórica por meses

ANÁLISE EXPLORATÓRIA

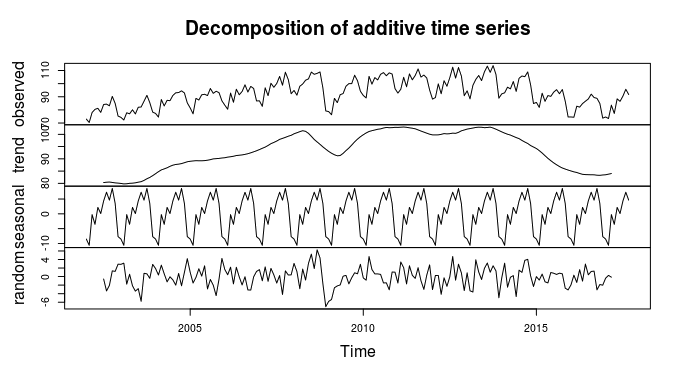
CONTINUAÇÃO

Olhando para o gráfico da decomposição da série, podemos identificar algumas características:

  • Foi extremamente afetada pela crise econômica.
  • Tem característica sazonal;
  • Apresenta uma tendência crescente antes da crise econômica e parece estar estável após;
  • Parece ter variação constante (próximo gráfico);

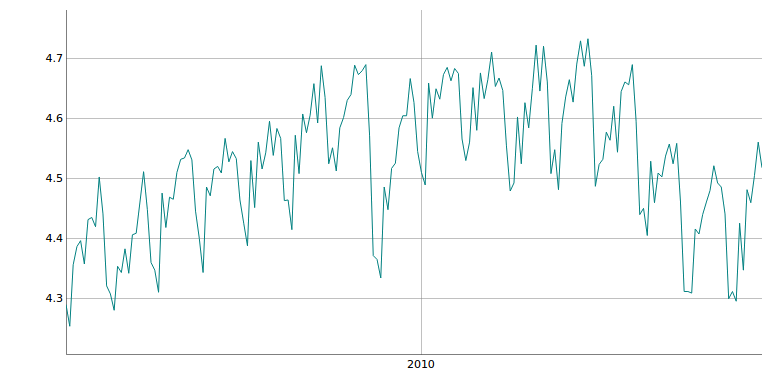
Dados transformados com log

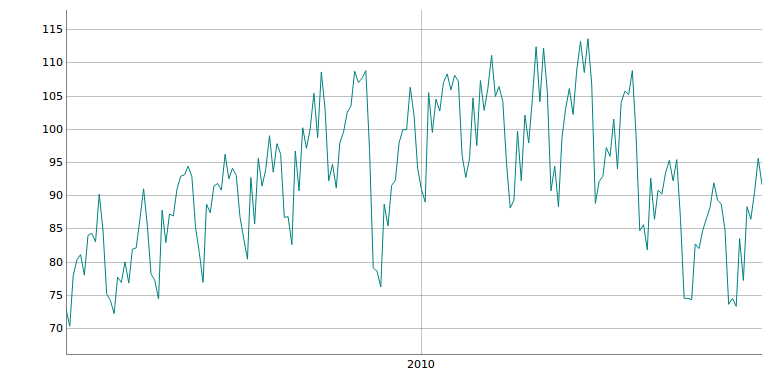
Dados sem transformação

CONTROLE DE VARIAÇÃO

ESTIMAÇÃO DO MODELO

Verificando estacionariedade

Observar os gráficos:

  • Autocorrelação
  • Autocorrelação parcial

Teste de estacionariedade: adf.test()

adf.test(dados)
Augmented Dickey-Fuller Test

data:  dados
Dickey-Fuller = -3.5417, Lag order = 5, 
p-value = 0.04036
alternative hypothesis: stationary

Gráfico de Autocorrelação

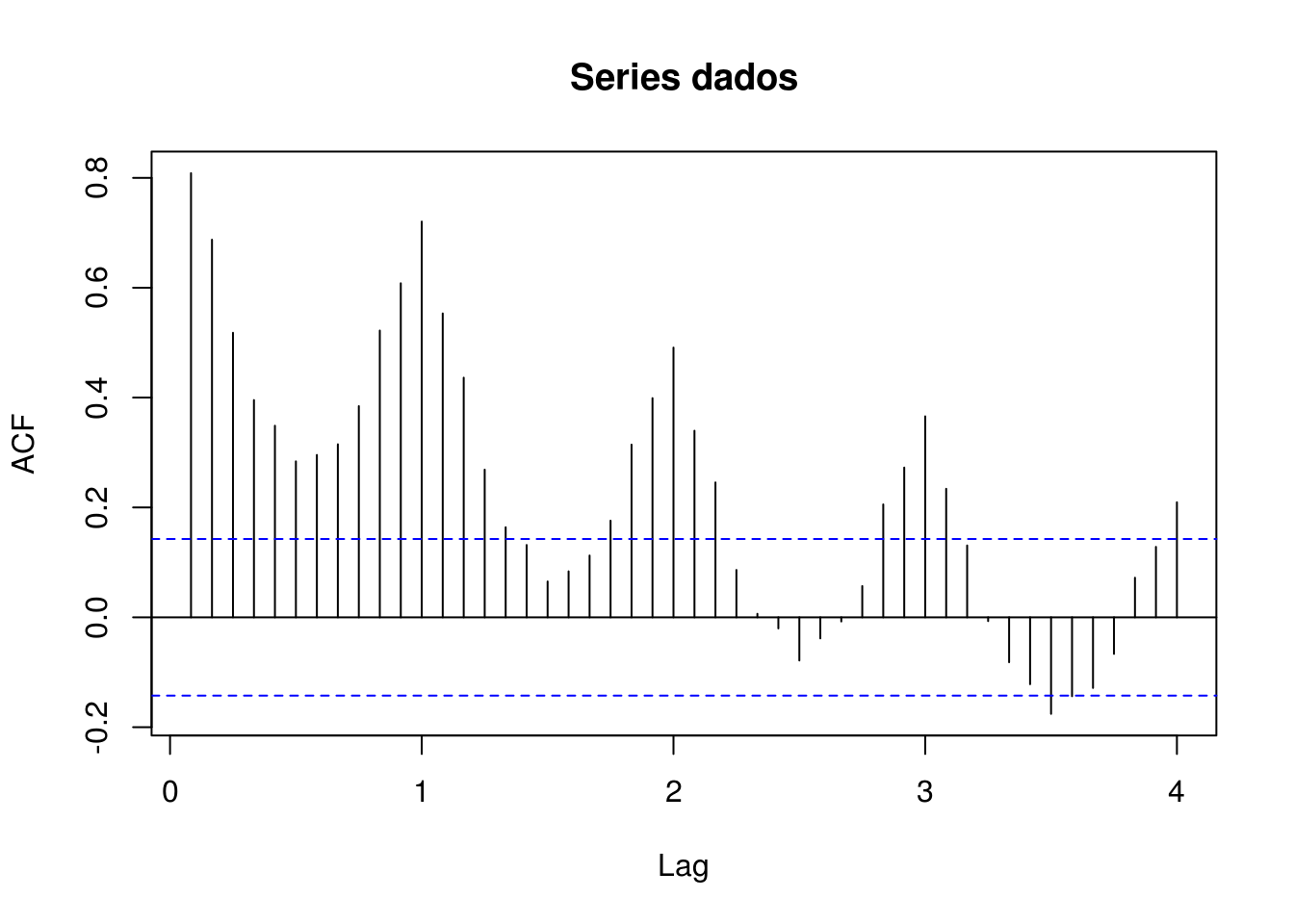
Gráfico de Autocorrelação

Com uma diferença

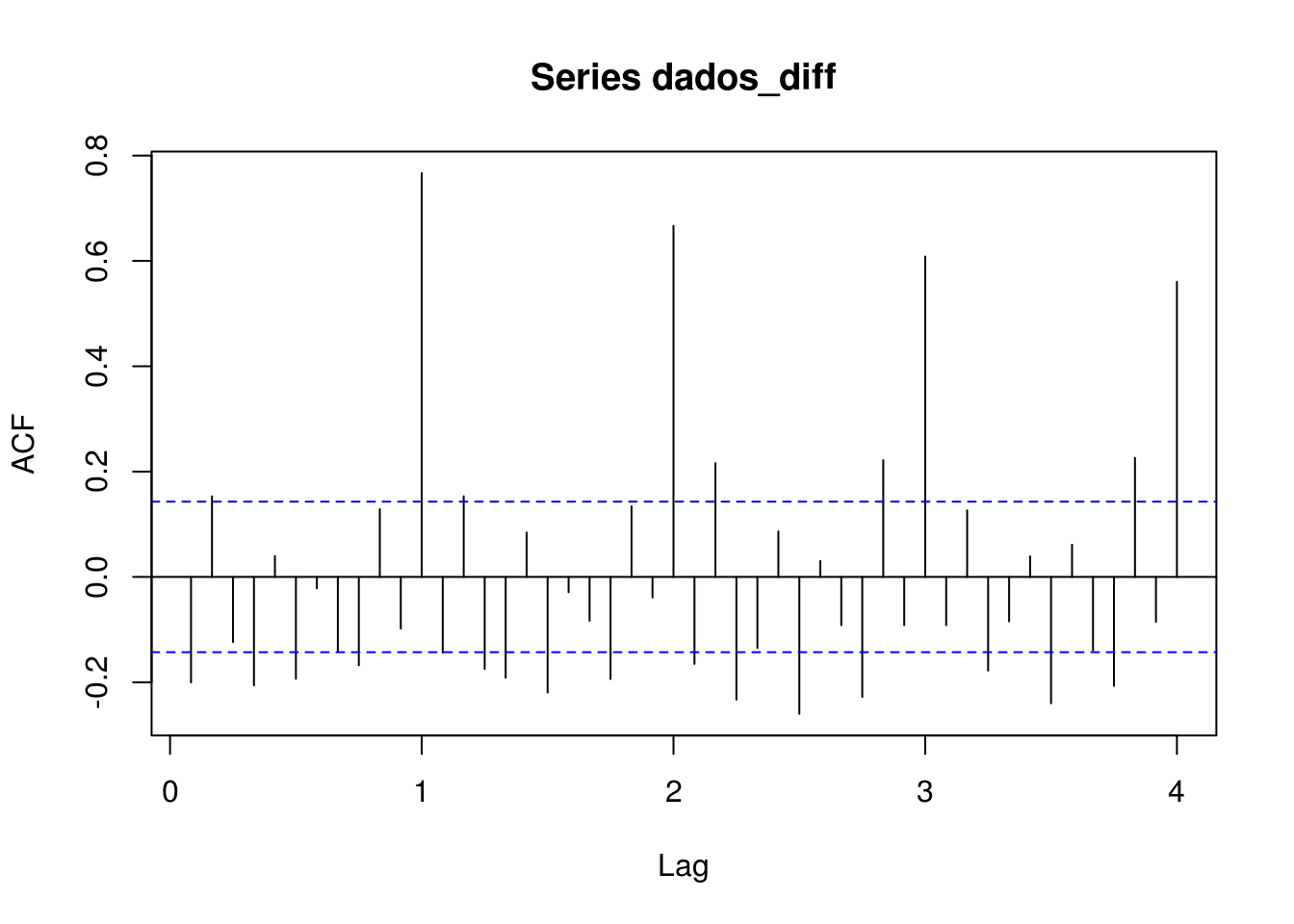
Gráfico de Autocorrelação

Com diferenciação sazonal dos dados diferenciados

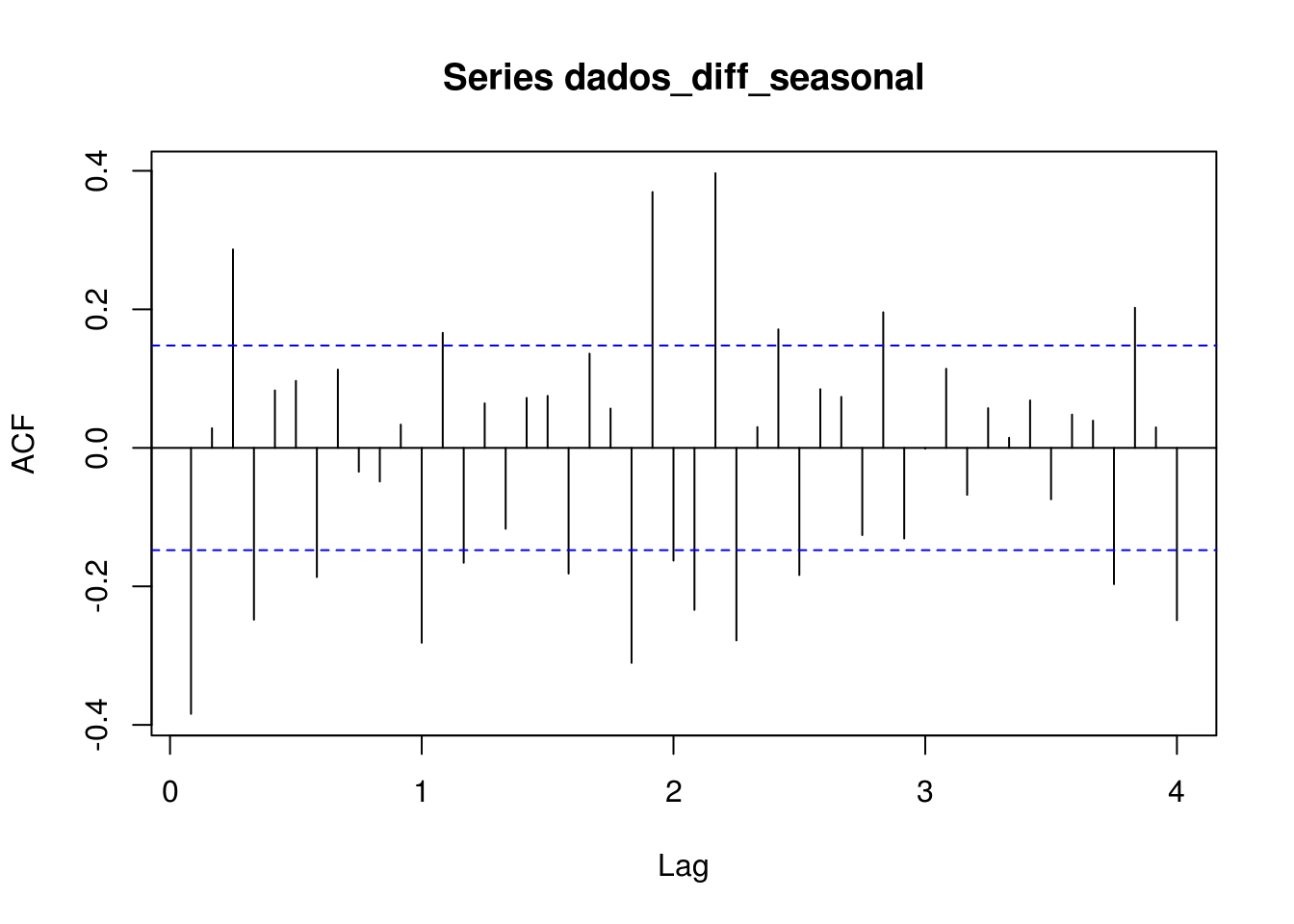
IDENTIFICANDO OS PARÂMETROS

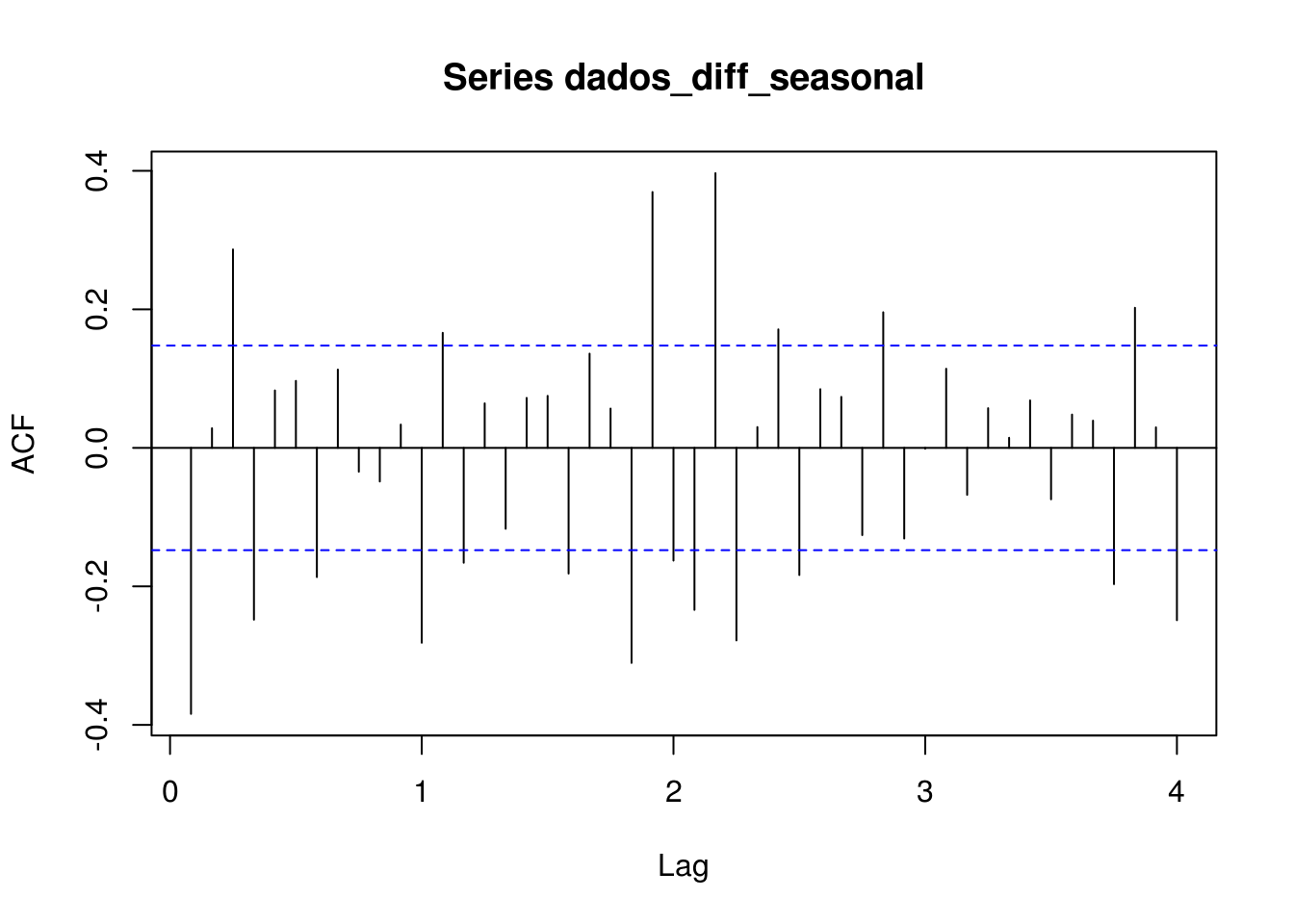
Médias Móveis

Podemos identificar uma ordem 2 para parte MA não sazonal e ordem 1 para a parte sazonal

Autorregresiva

Ordem 3 para a parte AR não sazonal e ordem 1 para a parte sazonal.

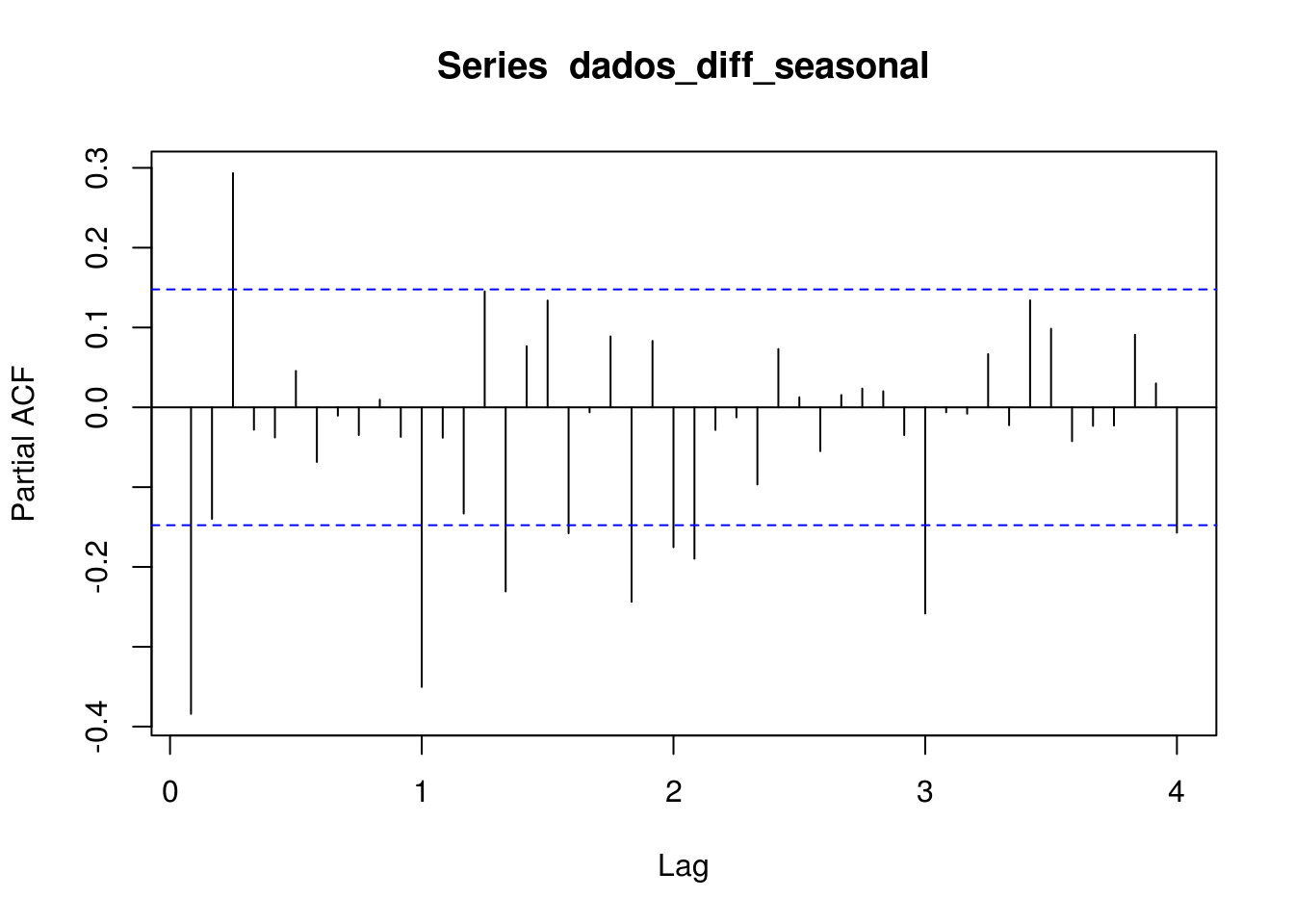
ESPECIFICAÇÃO DO MODELO

Encontramos o seguinte modelo:

SARIMA(3,1,2)(0,1,1)[12]

Verificando a significância dos parâmetros

(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}
(1−ϕ1B−ϕ2B2−ϕ3B3)ΔΔ12Xt=(1+θ1B+θ2B2)(1+Θ1B12)et(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t}
  Coeffs Std.Errors         t Crit.Values Rej.H0
ar1  -1.4494937 0.07524682 19.263190    1.973157   TRUE
ar2  -1.3408489 0.08622321 15.550904    1.973157   TRUE
ar3  -0.2956299 0.07478649  3.952985    1.973157   TRUE
ma1   1.1660209 0.02354924 49.514169    1.973157   TRUE
ma2   0.9993935 0.02867242 34.855570    1.973157   TRUE
sma1 -0.8075343 0.06415542 12.587157    1.973157   TRUE
BETS.t_test(modelo)
modelo = Arima(dados,order= c(3,1,2),seasonal = c(0,1,1),lambda = 0)

Verificando os resíduos

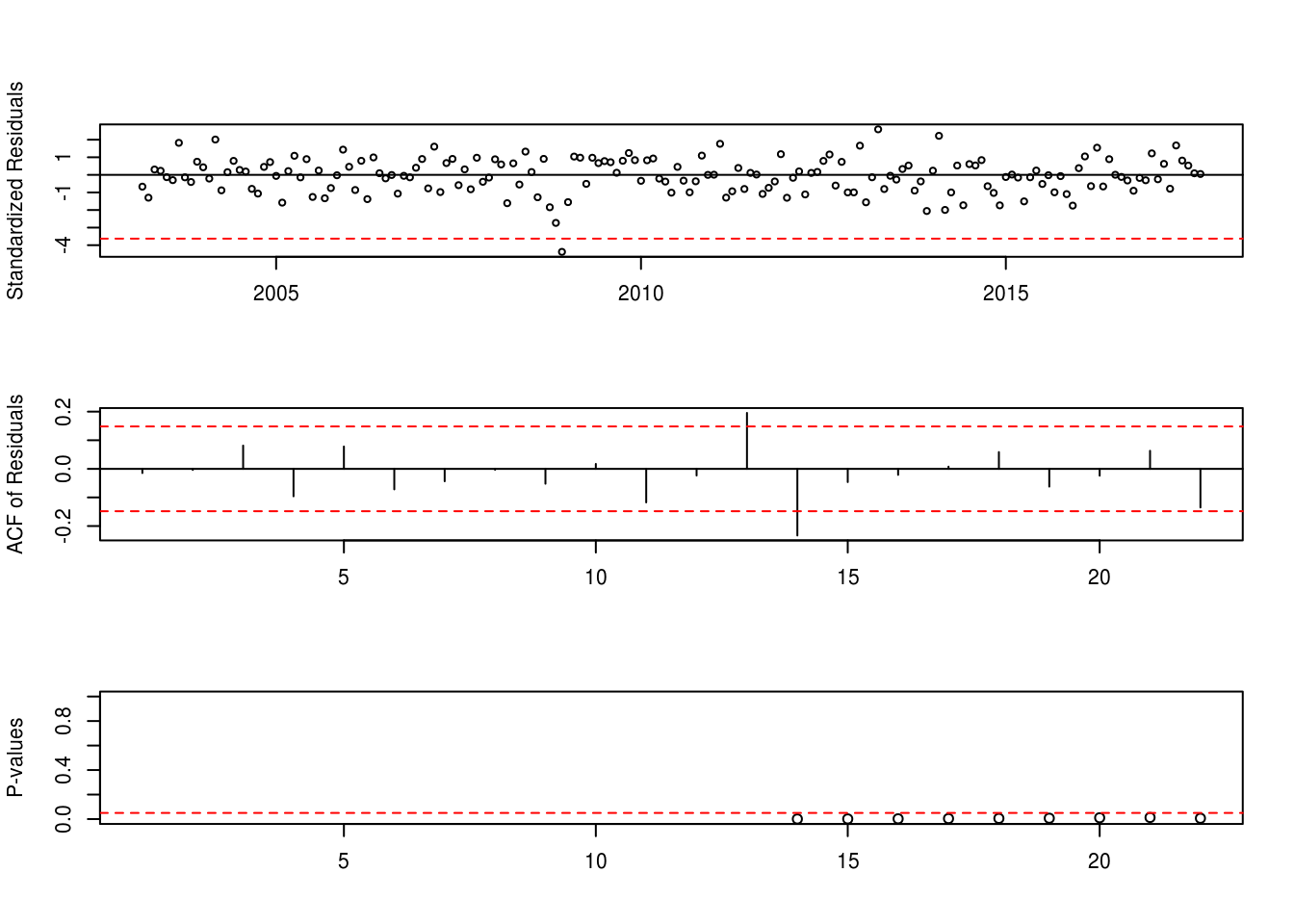
SARIMA(3,1,2)(0,1,1)[12]

Teste de Normalidade

shapiro.test(modelo$residuals)
## 
##  Shapiro-Wilk normality test
## 
## data:  modelo$residuals
## W = 0.97852, p-value = 0.005241

A crise econômica afeta muito a estimação do modelo pois temos presença de outlier. Precisamos identificá-los: 

##      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 2002   0   0   0   0   0   0   0   0   0   0   0   0
## 2003  -1   0  -1  -1   0   0   0   0   2   0   0   1
## 2004   1   0   2  -1   0   1   0   0  -1  -1   1   1
## 2005   0  -2   0   1   0   1  -1   0  -1  -1   0   2
## 2006   1  -1   1  -1   1   0   0   0  -1   0   0   0
## 2007   1  -1   2  -1   1   1  -1   0  -1   1   0   0
## 2008   1   1  -2   1  -1   1   0  -1   1  -2  -3  -5
## 2009  -2   1   1   0   1   1   1   1   0   1   1   1
## 2010   0   1   1   0   0  -1   1   0  -1   0   1   0
## 2011   0   2  -1  -1   0  -1   0   0  -1  -1   0   1
## 2012  -1   0   0  -1   0   0   1   1  -1   1  -1  -1
## 2013   2  -2   0   3  -1   0   0   0   1  -1   0  -2
## 2014   0   2  -2  -1   1  -2   1   1   1  -1  -1  -2
## 2015   0   0   0  -2   0   0   0   0  -1   0  -1  -2
## 2016   0   1  -1   2  -1   1   0   0   0  -1   0   0
## 2017   1   0   1  -1   2   1   1   0   0
aux  =  (modelo$residuals - mean(modelo$residuals))
aux2 =  sd(modelo$residuals)

x = aux/ aux2

round(x)

Valor discrepante em dez/2008

Para controlar o resíduo discrepante, criamos uma variável dummy.
Utilizando a função BETS.dummy(), temos:

Controlando os resíduos

dummy <-  BETS.dummy(start = c(2002,01),end = c(2017,09),month =12 ,year = 2008 ,frequency = 12)

##      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 2002   0   0   0   0   0   0   0   0   0   0   0   0
## 2003   0   0   0   0   0   0   0   0   0   0   0   0
## 2004   0   0   0   0   0   0   0   0   0   0   0   0
## 2005   0   0   0   0   0   0   0   0   0   0   0   0
## 2006   0   0   0   0   0   0   0   0   0   0   0   0
## 2007   0   0   0   0   0   0   0   0   0   0   0   0
## 2008   0   0   0   0   0   0   0   0   0   0   0   1
## 2009   0   0   0   0   0   0   0   0   0   0   0   0
## 2010   0   0   0   0   0   0   0   0   0   0   0   0
## 2011   0   0   0   0   0   0   0   0   0   0   0   0
## 2012   0   0   0   0   0   0   0   0   0   0   0   0
## 2013   0   0   0   0   0   0   0   0   0   0   0   0
## 2014   0   0   0   0   0   0   0   0   0   0   0   0
## 2015   0   0   0   0   0   0   0   0   0   0   0   0
## 2016   0   0   0   0   0   0   0   0   0   0   0   0
## 2017   0   0   0   0   0   0   0   0   0

Remodelando

Agora introduzindo a variável dummy no modelo, com o parâmetro xreg

modelo2 <- Arima(dados,order= c(3,1,2),seasonal = c(0,1,1),lambda = 0,xreg=dummy)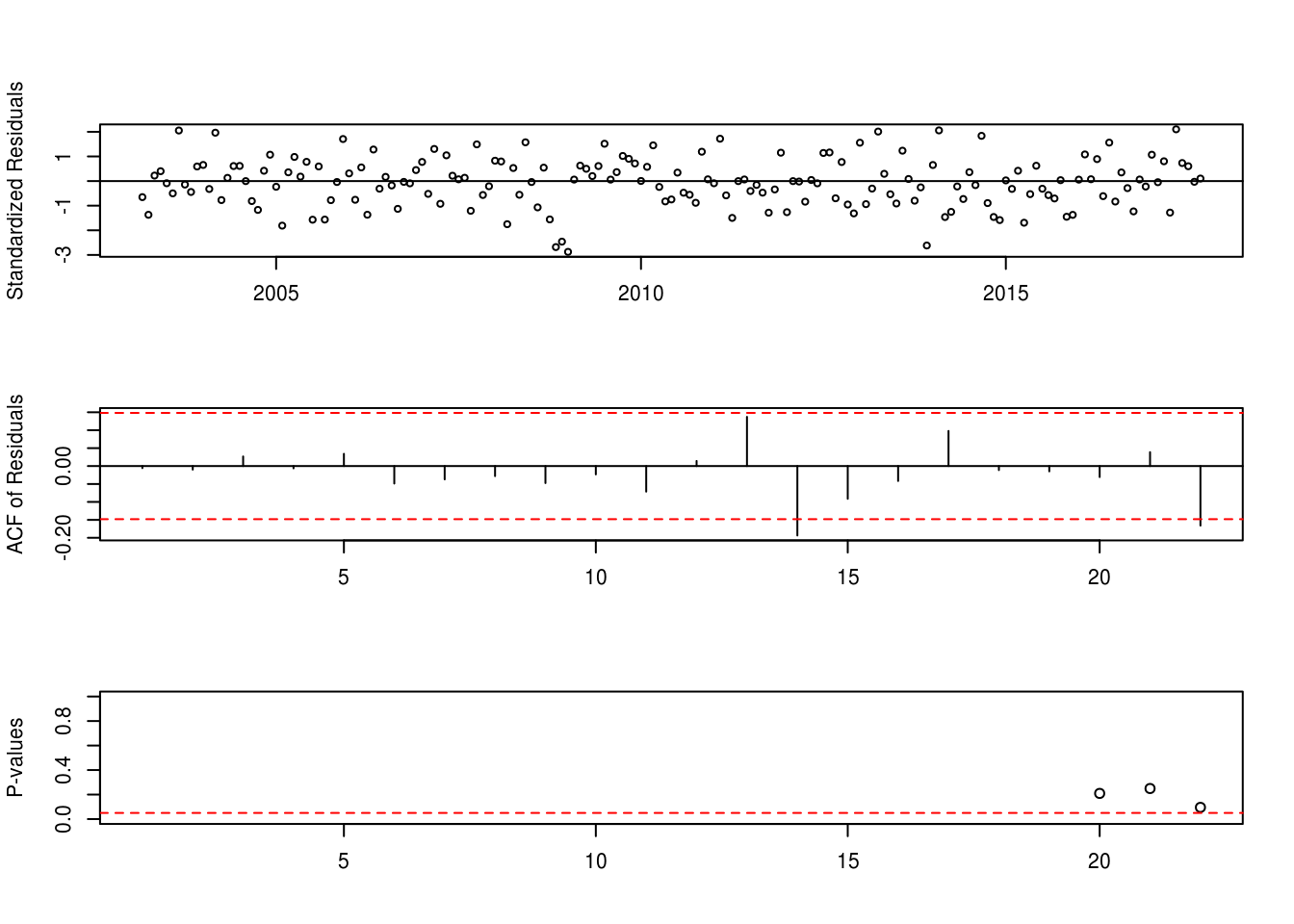
tsdiag(modelo2)
(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t} + \beta D_{t}
(1−ϕ1B−ϕ2B2−ϕ3B3)ΔΔ12Xt=(1+θ1B+θ2B2)(1+Θ1B12)et+βDt(1 - \phi_{1}B - \phi_{2}B^{2} - \phi_{3}B^{3})\Delta\Delta_{12}X_{t} = (1 + \theta_{1}B + \theta_{2}B^{2})(1 + \Theta_{1}B^{12})e_{t} + \beta D_{t}
D_{t} = \left \{ \begin{matrix} 1 &,& t = \text{ Dez de 2008 } \\ 0 &,& \text{c.c} \end{matrix} \right.
Dt={1,t= Dez de 2008 0,c.c D_{t} = \left \{ \begin{matrix} 1 &amp;,&amp; t = \text{ Dez de 2008 } \\ 0 &amp;,&amp; \text{c.c} \end{matrix} \right.

Modelo Considerando a v.a. Dummy

shapiro.test(modelo2$residuals)
## 
##  Shapiro-Wilk normality test
## 
## data:  modelo2$residuals
## W = 0.98781, p-value = 0.1039
BETS.t_test(modelo2)
##            Coeffs Std.Errors          t Crit.Values Rej.H0
## ar1   -1.08991947 0.30593140  3.5626270    1.973157   TRUE
## ar2   -0.89770178 0.36031799  2.4914153    1.973157   TRUE
## ar3   -0.04273486 0.20991138  0.2035852    1.973157  FALSE
## ma1    0.70873332 0.30279401  2.3406451    1.973157   TRUE
## ma2    0.55931671 0.23620363  2.3679429    1.973157   TRUE
## sma1  -0.78668213 0.06967847 11.2901757    1.973157   TRUE
## dummy -0.07727876 0.02191596  3.5261406    1.973157   TRUE

O terceiro parâmetro não é significativo, ele deve ser retirado do modelo!

Verificando os resíduos

SARIMA(3,1,2)(0,1,1)[12] + dummy

Remodelando

modelo3 <- Arima(dados,order = c(2,1,2),seasonal = c(0,1,1),lambda = 0,xreg=dummy)
tsdiag(modelo3)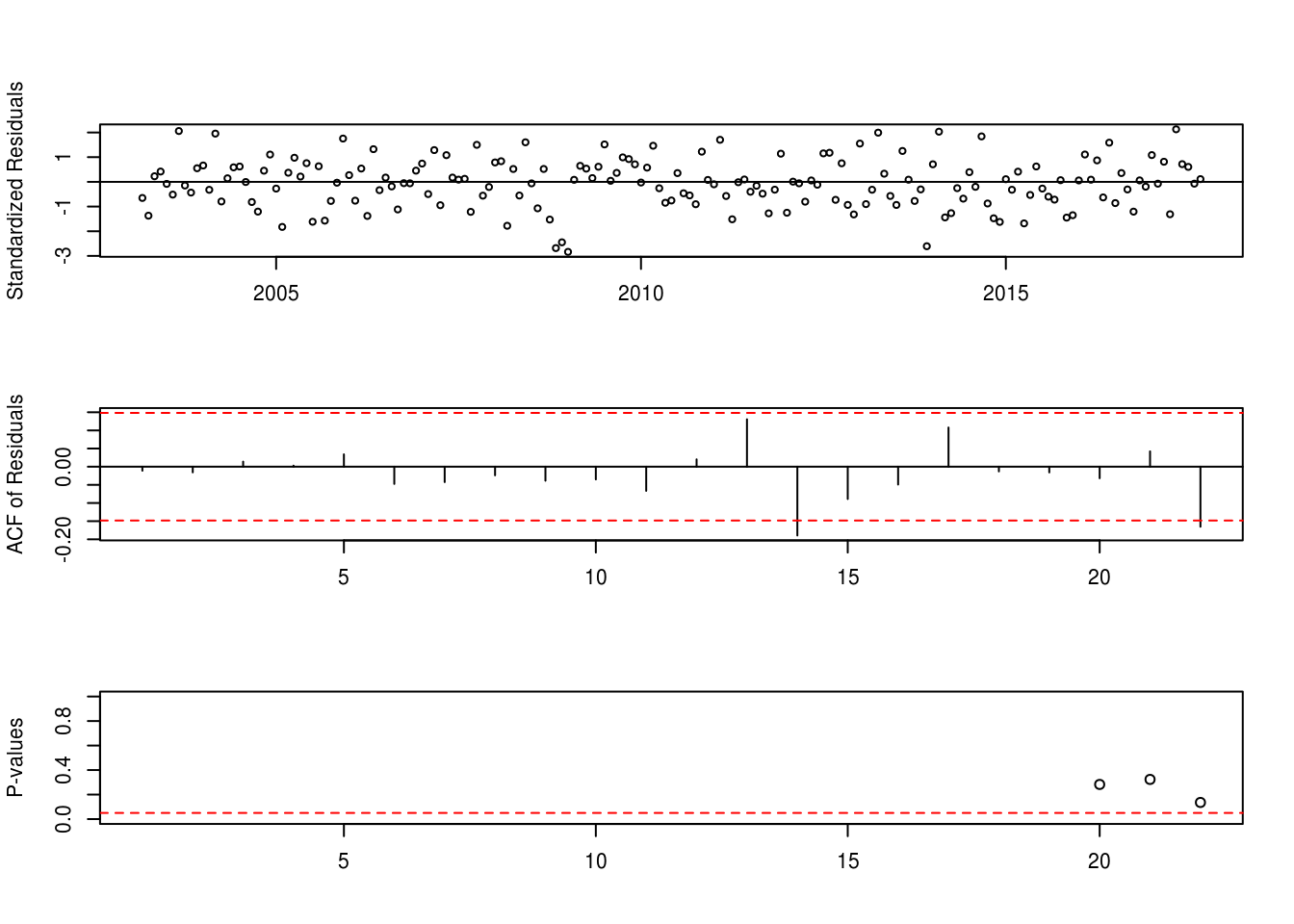
shapiro.test(modelo3$residuals)
## 
##  Shapiro-Wilk normality test
## 
## data:  modelo3$residuals
## W = 0.98885, p-value = 0.1457

PREVISÃO

Na modelagem, fizemos dois tipos de previsão para os dados referente a 2017, de janeiro a setembro:

Previsão mês a mês, ou seja 1 passo, sucessivamente, a frente de janeiro até a setembro;

Previsão, 9 passos a frente, de uma vez só.

Jan - Set/17

Jan/2002 - Dez/2016

Amostra

Previsão

Desenvolvemos uma  função para o cálculo para os dois tipo de previsão

prev <- funcao_prev( h=h,dados=dados,order=order,seasonal = seasonal,lambda = 0)
  • h é a quantidade de valores que queremos prever;
  • dados ferente aos dados, série temporal em estudo;
  • order é a ordem autorregressiava do nosso modelo geral SARIMA;
  • seasonal é a ordem da parte sazonal do nosso modelo geral SARIMA;
  • lambda é referente a transformação dos dados em log(x).

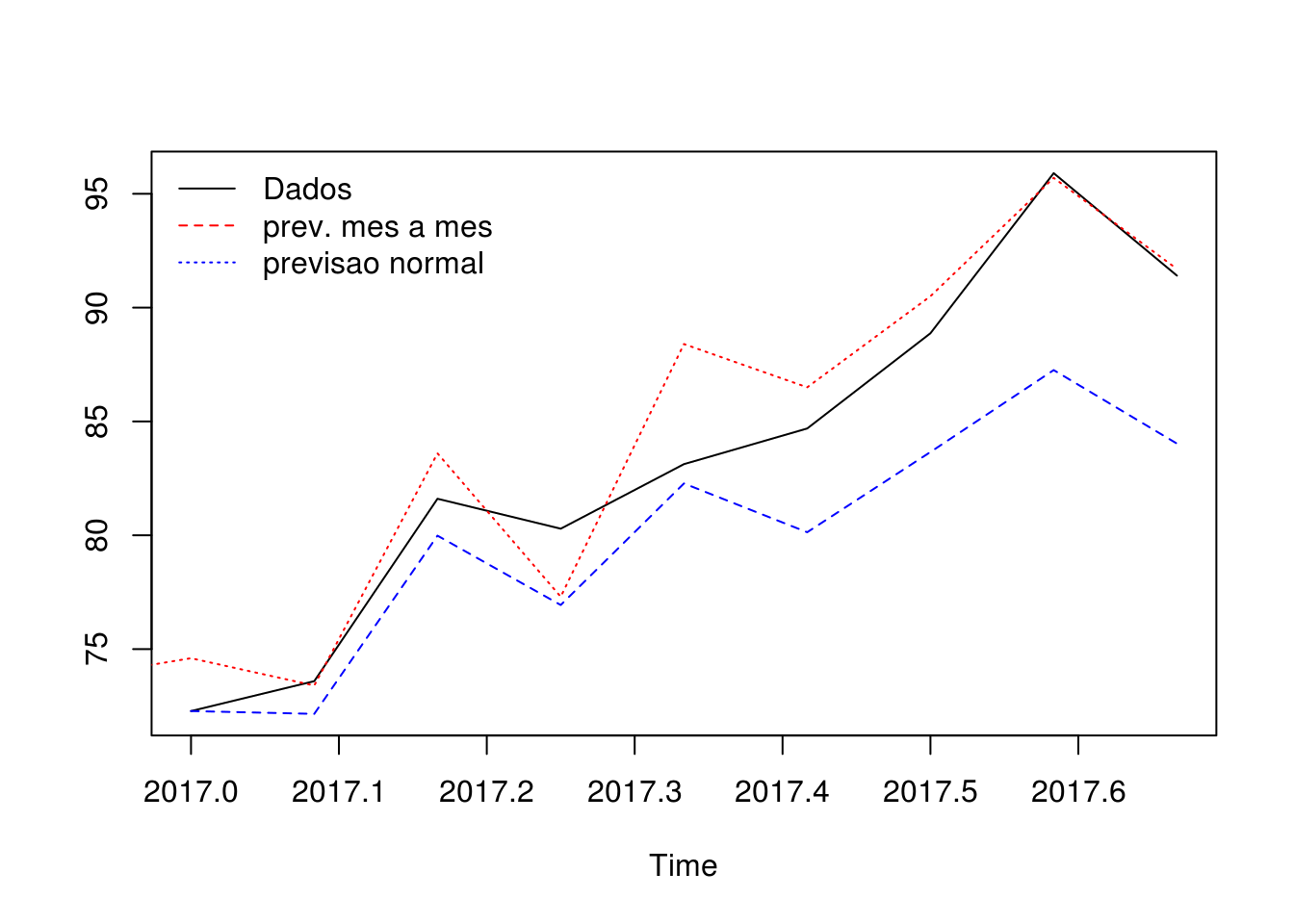
PREV 1 é a previsão mês a mês

PREV 2 é a previsão 9 passos à frente

MEDIDAS DE ERRO

ERRO  MÉDIO QUADRÁTICO

ERRO ABSOLUTO PERCENTUAL MÉDIO

mean((comparacao - prev$prev1)^2)

5.8

30.5

mean((comparacao - prev$prev2)^2)
mean(abs(comparacao - prev$prev1)/comparacao)*100
mean(abs(comparacao - prev$prev2)/comparacao)*100

2.2%

5.4%

CONCLUSÃO

Com o trabalho utilizando os dados da produção industrial, conseguimos colocar todo o conhecimento obtido no curso

Quebra estrutural

A PIM-PF é uma série mais desafiante

Conseguimos verificar diferentes modelos

Buscar mais evidências e não se basear 100% nos testes estatísticos de forma cega, análise exploratória é fundamental

E o trabalho, acaba sendo uma forma de aumentar o conhecimento no final do curso

Algumas Referências

BOX, G.E.P.; JENKINS, G.M.; REINSEL, G.C.; LJUNG, G.M. Time Series Analysis: Forecasting and Control. 5ª edição. 2016.

ESPINOSA, M.M.; PRADO, S.M.; GHELLERE, M. Uso do modelo SARIMA na previsão do número de focos de calor para os meses de junho a outubro no Estado de Mato Grosso. Ciência e Natura. Volume 32, 2ª edição. Págs. 7-21. 2010.

OBRIGADO!

Made with Slides.com