Basisconcepten

Logische bewering P is waar/onwaar (1/0)
Samengestelde beweringen door beweringen P,Q te combineren:
- conjunctie, en \( \wedge\)
- disjunctie, of \( \vee\)
- ontkenning, niet \( \neg\)
- implicatie, \( \Rightarrow\)
- equivalentie \( \Leftrightarrow\)
  
  en de samengestelde bewering in haar geheel is terug waar/onwaar

Basisconcepten

Waarheidstabel
- Nuttige tool om waarheidswaarde van samengestelde bewering na te gaan!
- Bevat alle mogelijke combinaties van waar/onwaar van de componenten van de samengestelde bewering
- Volledige beschrijving van de samengestelde bewering
Kwantoren zijn handig als we logische uitspraken willen doen over elementen van verzamelingen
- Universeel \( \forall x \in A: P(x) \)
- Existentieel \( \exists x \in A: Q(x) \)
Net zoals bij verzamelingen, zijn er hier rekenregels

Oefeningen

Oefening 2.6

Waarheidstabel `exclusieve of': P\(\ \oplus\) Q

1	1	0
1	0	1
0	1	1
0	0	0

P\(\ \oplus\) Q

Oefening 2.10

Stel dat P ⇒ Q waar is, en P is onwaar: wat kunnen we dan
besluiten over Q?

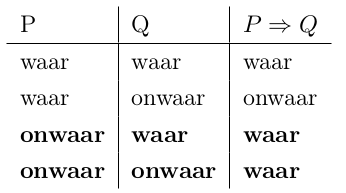
Q kan zowel waar als onwaar zijn. We kunnen dus niks besluiten.

Oefening 2.16

K = de letter is een klinker
E = het cijfer is even

de implicatie die moet gelden is dan K => E.

A B 5 X 6 E F 2

Als de letter een klinker is, moet het cijfer op de andere kant even zijn. Hoeveel kaartjes moet je omdraaien?

Oefening 2.16

K = de letter is een klinker
E = het cijfer is even
K => E.

A B 5 X 6 E F 2

De letter A maakt K waar, dus moet worden nagegaan of het cijfer voor deze kaart even is: anders is de implicatie onwaar.
De letter B maakt K onwaar, waardoor de implicatie automatisch waar is, dus deze kaart hoeft niet omgedraaid te worden.
Het cijfer 5 is niet even, dus mag de letter op de andere kant geen klinker zijn (volgens modus tollens!), dus deze kaart moet ook omgedraaid worden.
X maakt ook K onwaar, dus deze kaart hoeft niet omgedraaid te worden.
6 maakt E waar, dus hier is de implicatie ook automatisch waar; deze kaart hoeft niet omgedraaid te worden.
Op soortgelijke wijze kunnen we bepalen dat van de overige kaarten, alleen E hoeft te worden omgedraaid.
Uiteindelijk 3 kaartjes om te draaien!

Oefening 2.24

Toon aan dat P ⇒ Q logisch equivalent is met ¬P ∨ Q.

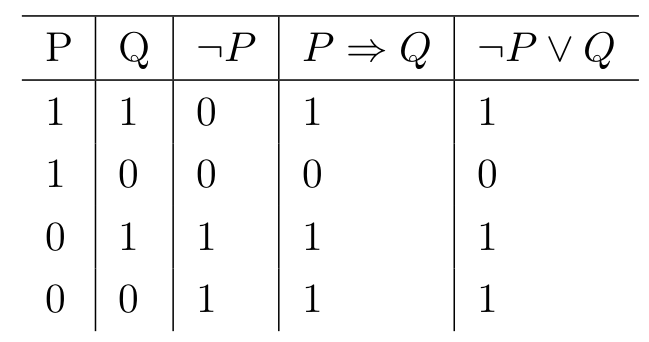
Oefening 2.26

Welk van deze beweringen zijn altijd waar, soms waar (afhankelijk van A en B), of nooit waar

\forall x \in A \cap B: x \in A

\forall x \in A \cup B: x \in A

Altijd waar, (\(x\) in doorsnede).
N.b.: Dit is ook zo als \(A\) de lege verzameling is!

Soms waar. (\(x\) in unie)

Oefening 2.31

Verbind wat equivalent is

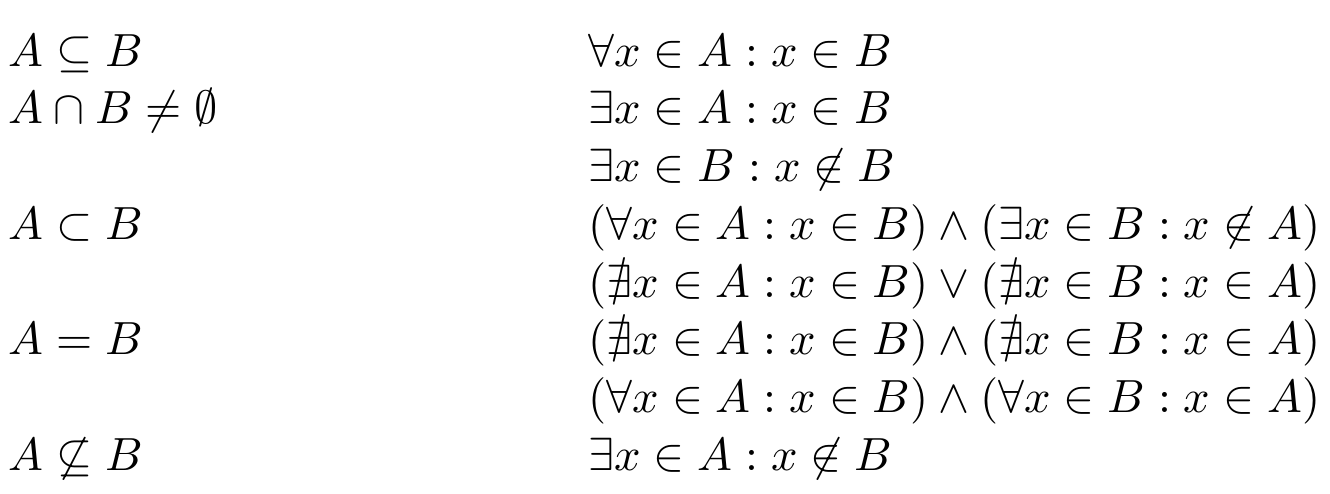
Oefening 2.38

Toon aan dat P ∧Q ⇒ P ∨Q een tautologie is, door rekenregels toe te passen.

P\wedge Q\Rightarrow P\vee Q \equiv \neg(P\wedge Q)\vee P\vee Q\\ \equiv (\neg P\vee\neg Q)\vee P\vee Q \\ \equiv \neg P\vee P\vee\neg Q\vee Q \\ \equiv \text{waar}\vee\text{waar} \\ \equiv \text{waar}. \\