Basisconcepten

Een relatie \( R \subseteq A \times A \)

• reflexief:
  \( \forall x \in A: (x,x) \in R \)
• anti-reflexief:
  \( \forall x \in A: (x, x) \notin R \) 
• symmetrisch:
  \( \forall x,y \in A: (x,y) \in R \Leftrightarrow (y,x) \in R \)
• anti-symmetrisch:
  \( \forall x,y \in A: (x,y) \in R \wedge (y,x) \in R \Rightarrow x = y \)
• Transitief:
  \( \forall x,y,z \in A: (x,y) \in R \wedge (y,z) \in R \Rightarrow (x,z) \in R \)

Basisconcepten

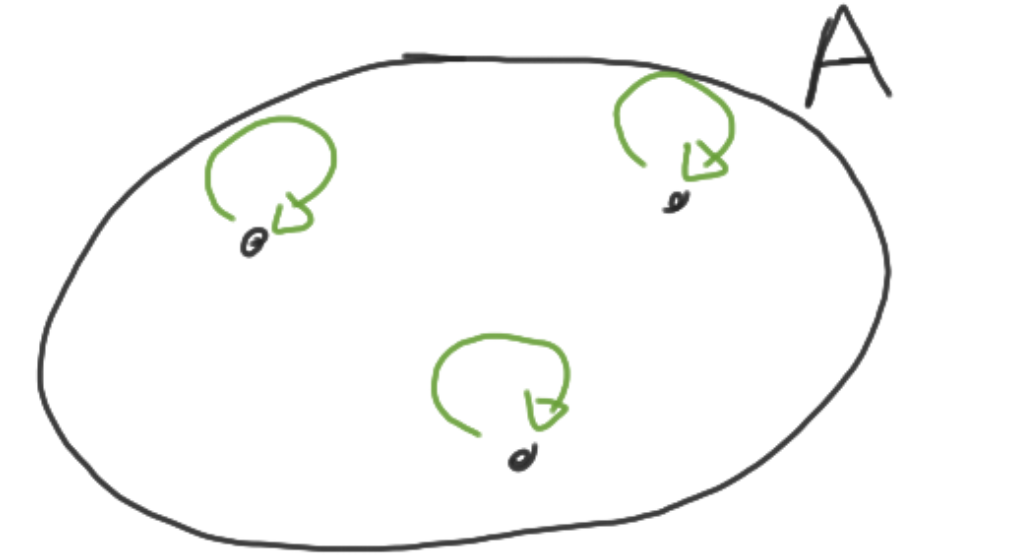
Reflexief

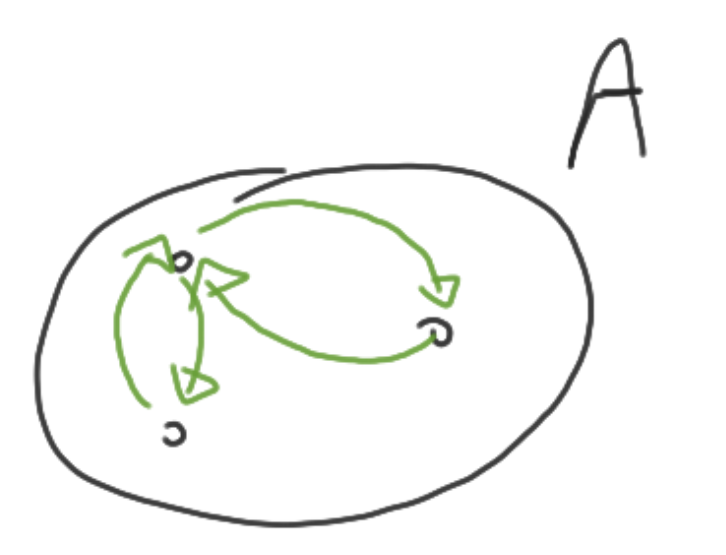
Symmetrisch

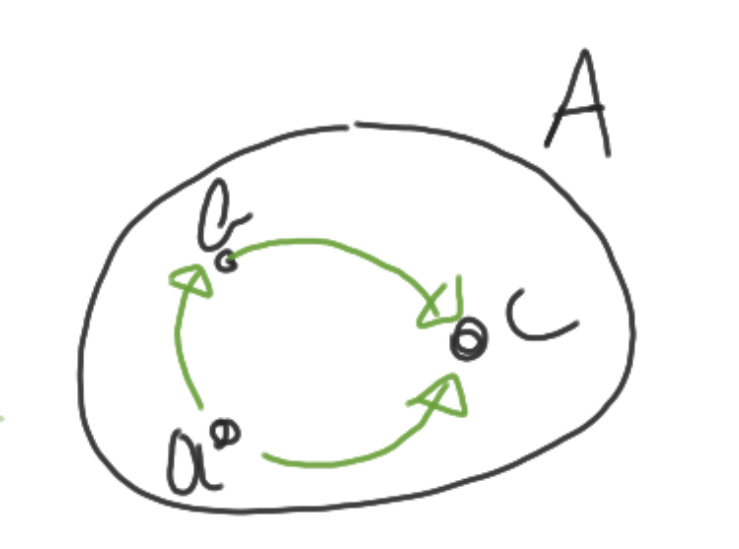
Transitief

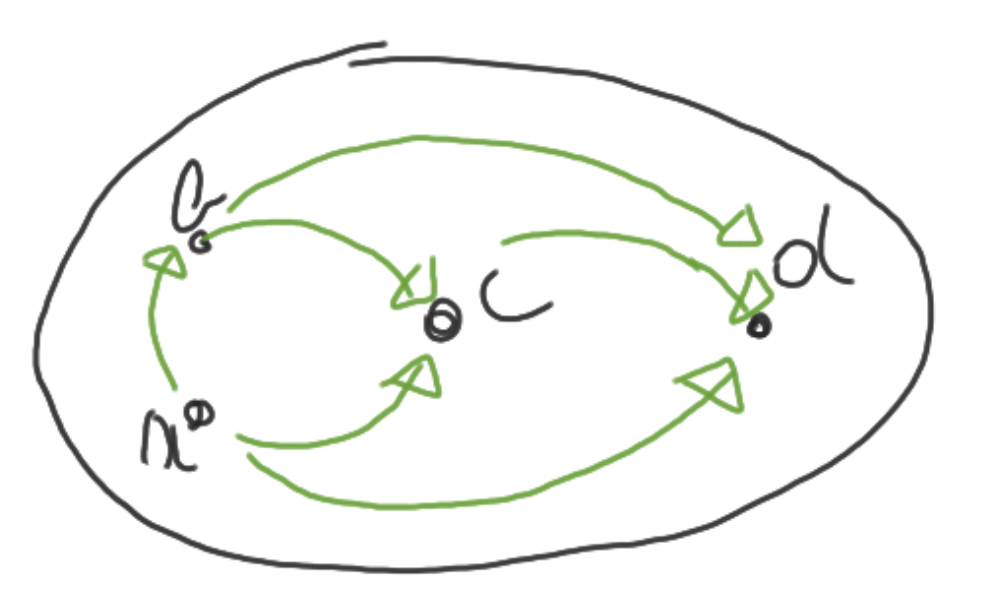
Basisconcepten

Equivalentierelatie: reflexief, symmetrisch en transitief

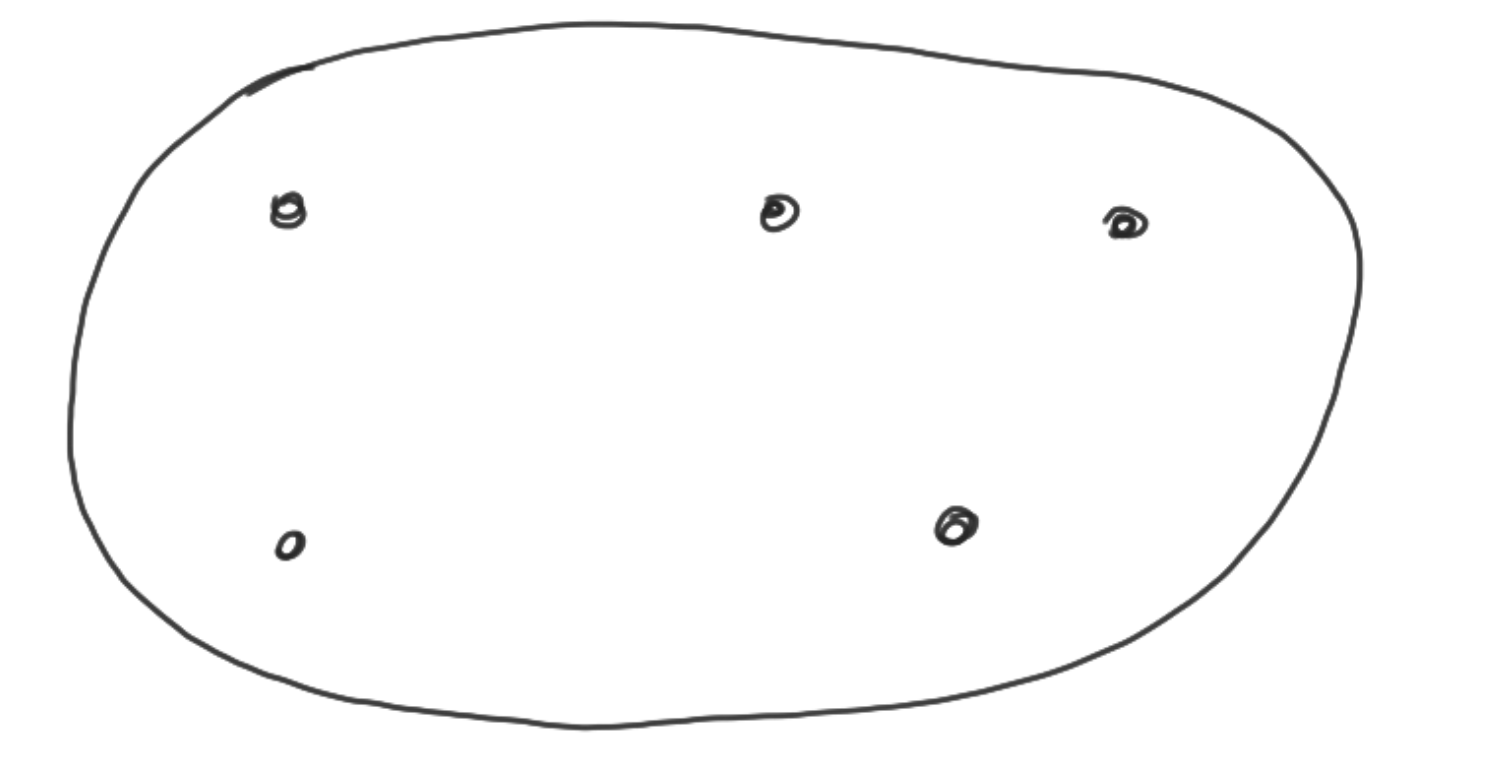
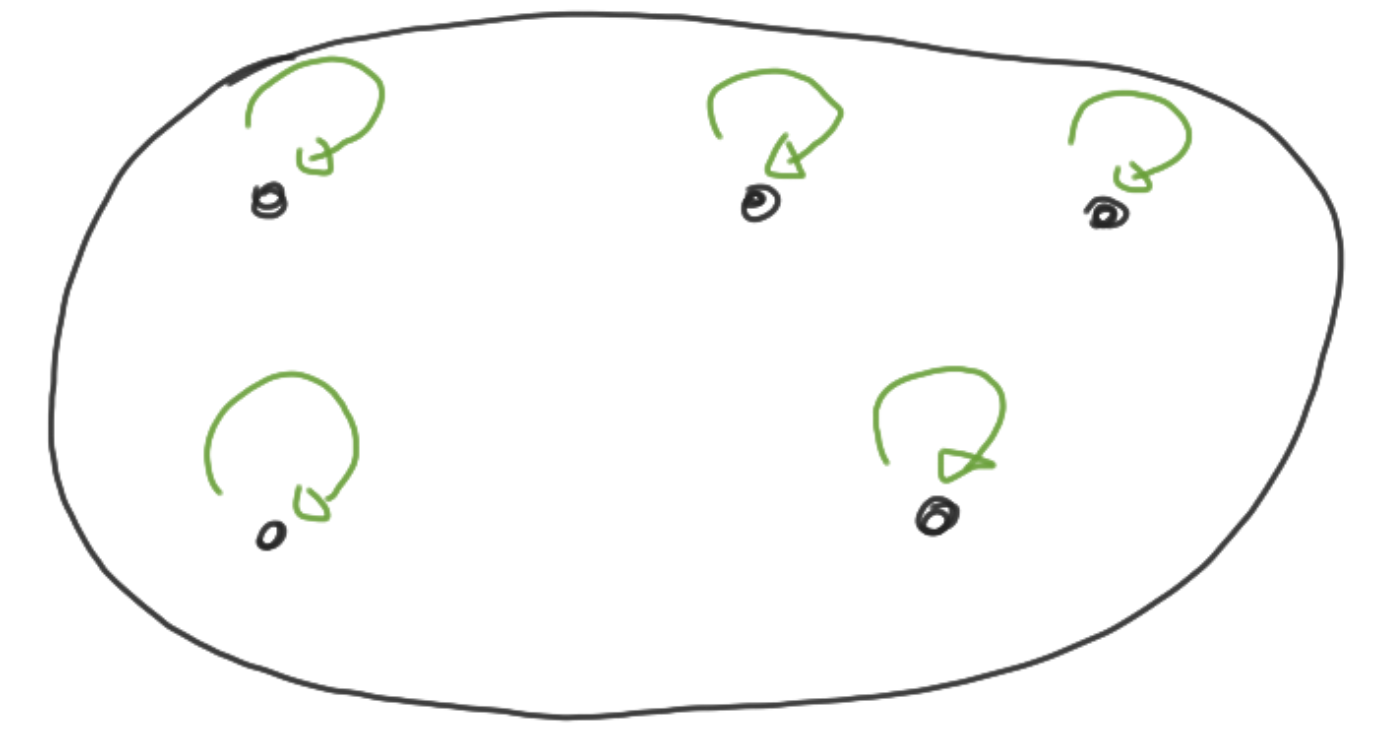
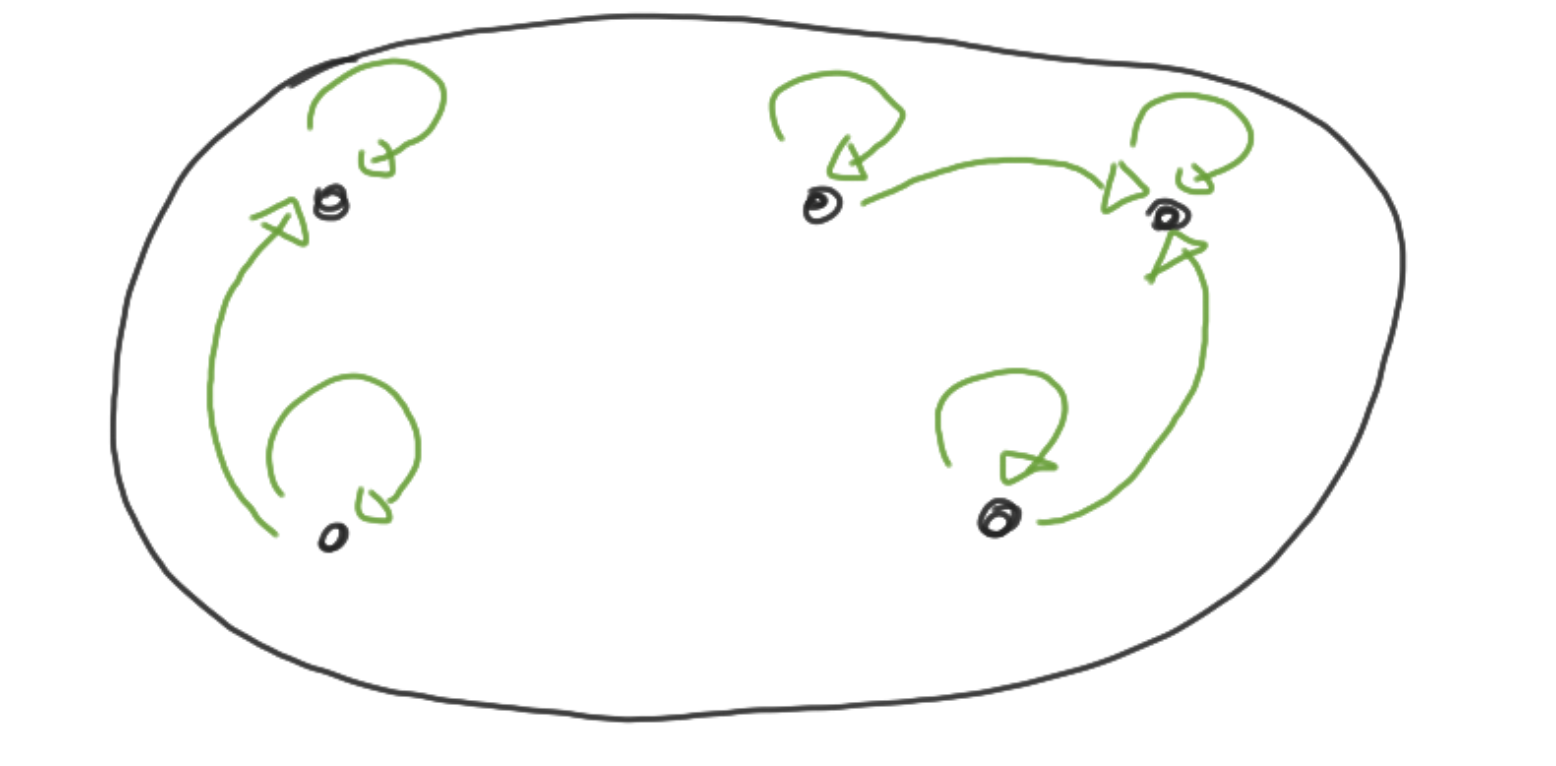
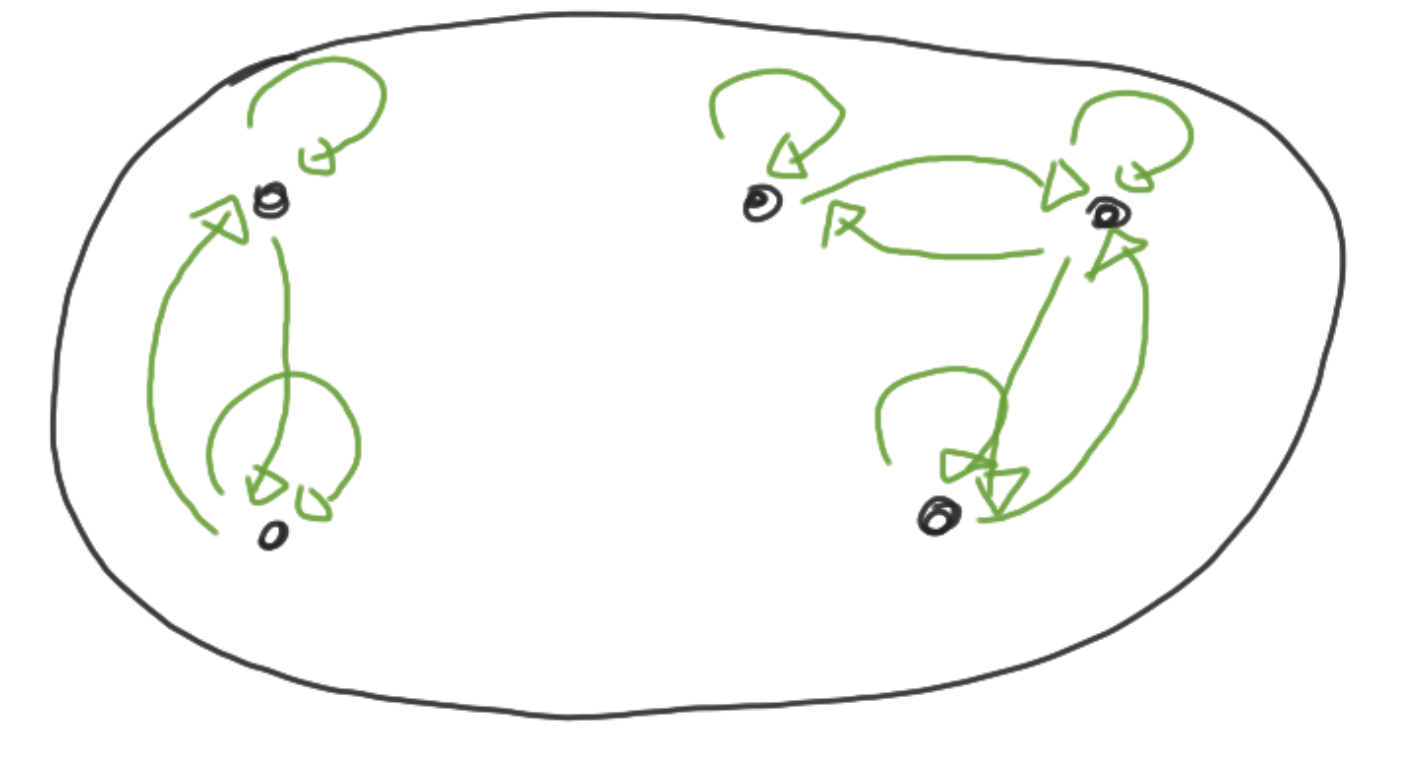
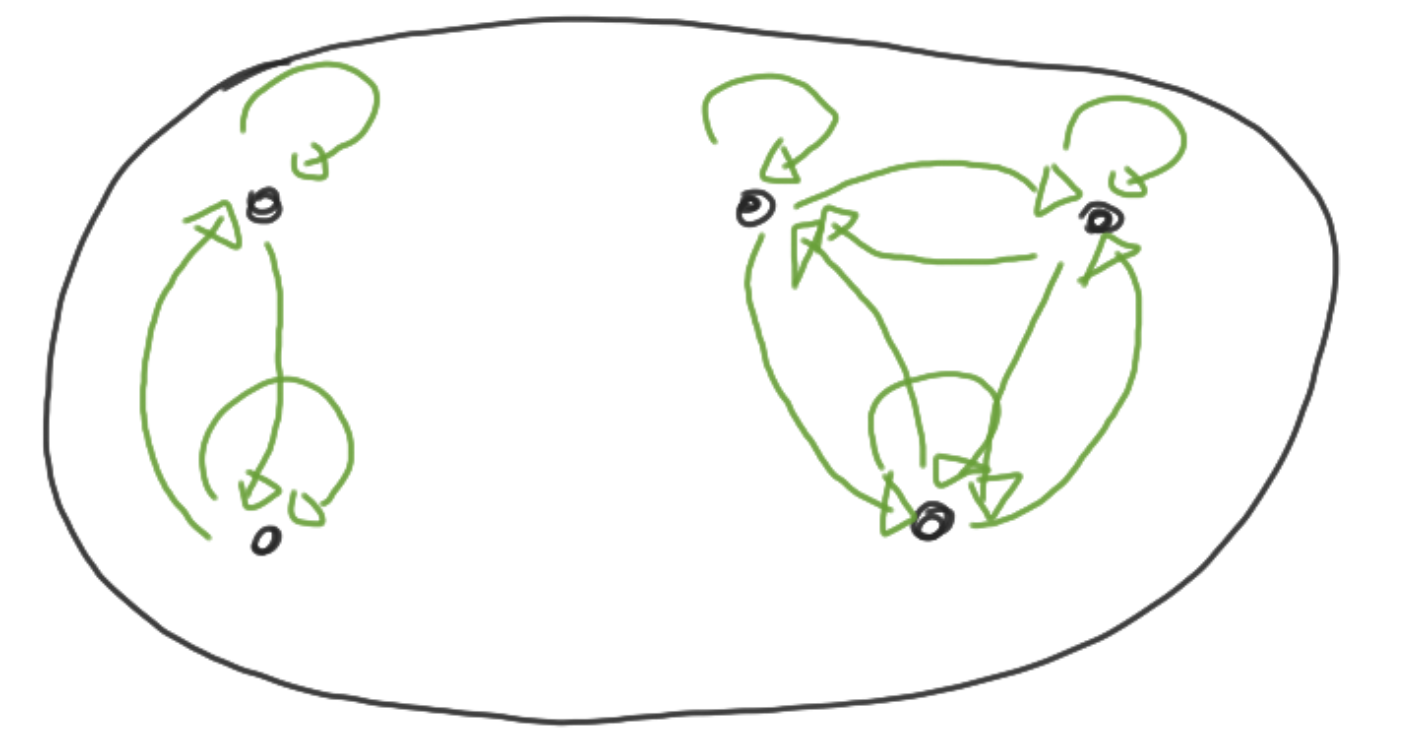
Basisconcepten

Orderelatie: reflexief, anti-symmetrisch en transitief

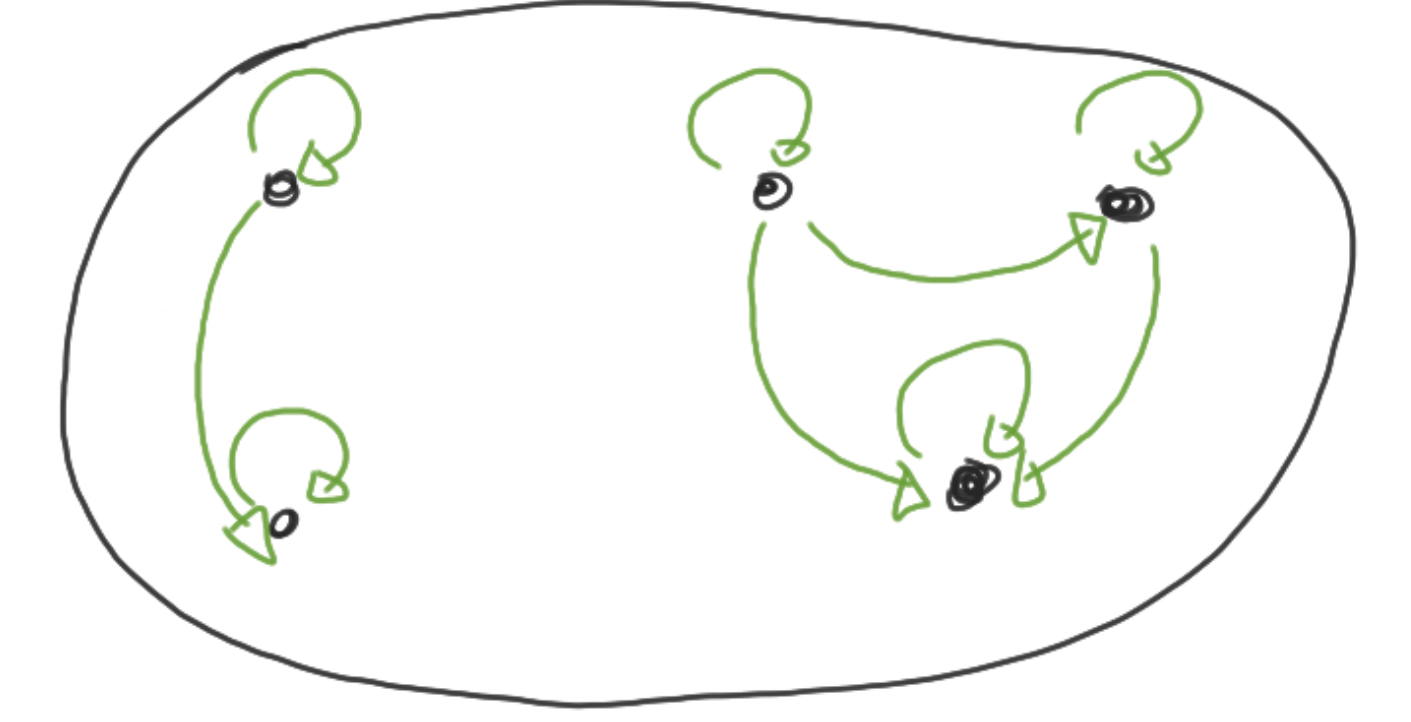
Totale orde en partiële orde

Basisconcepten

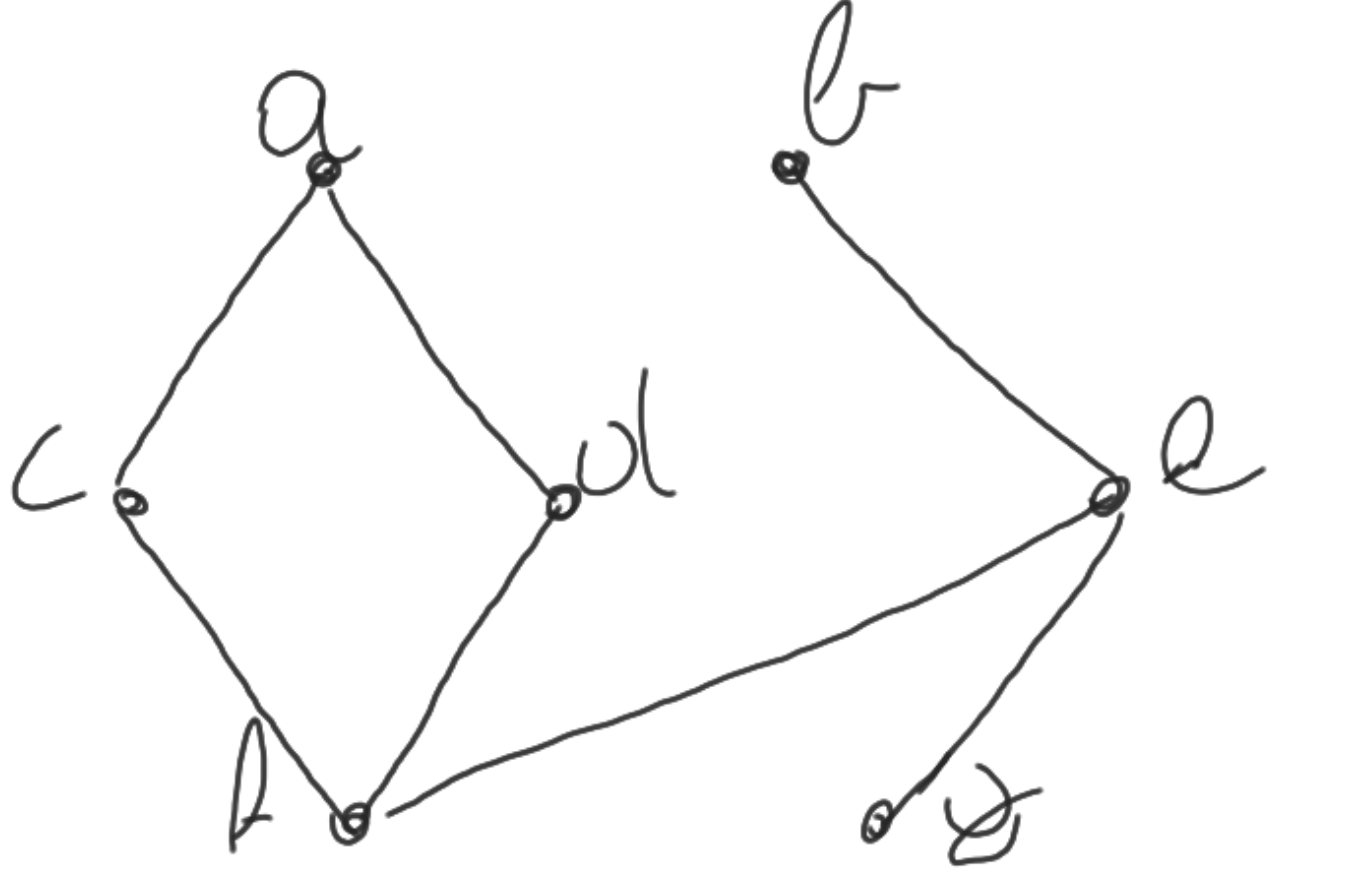
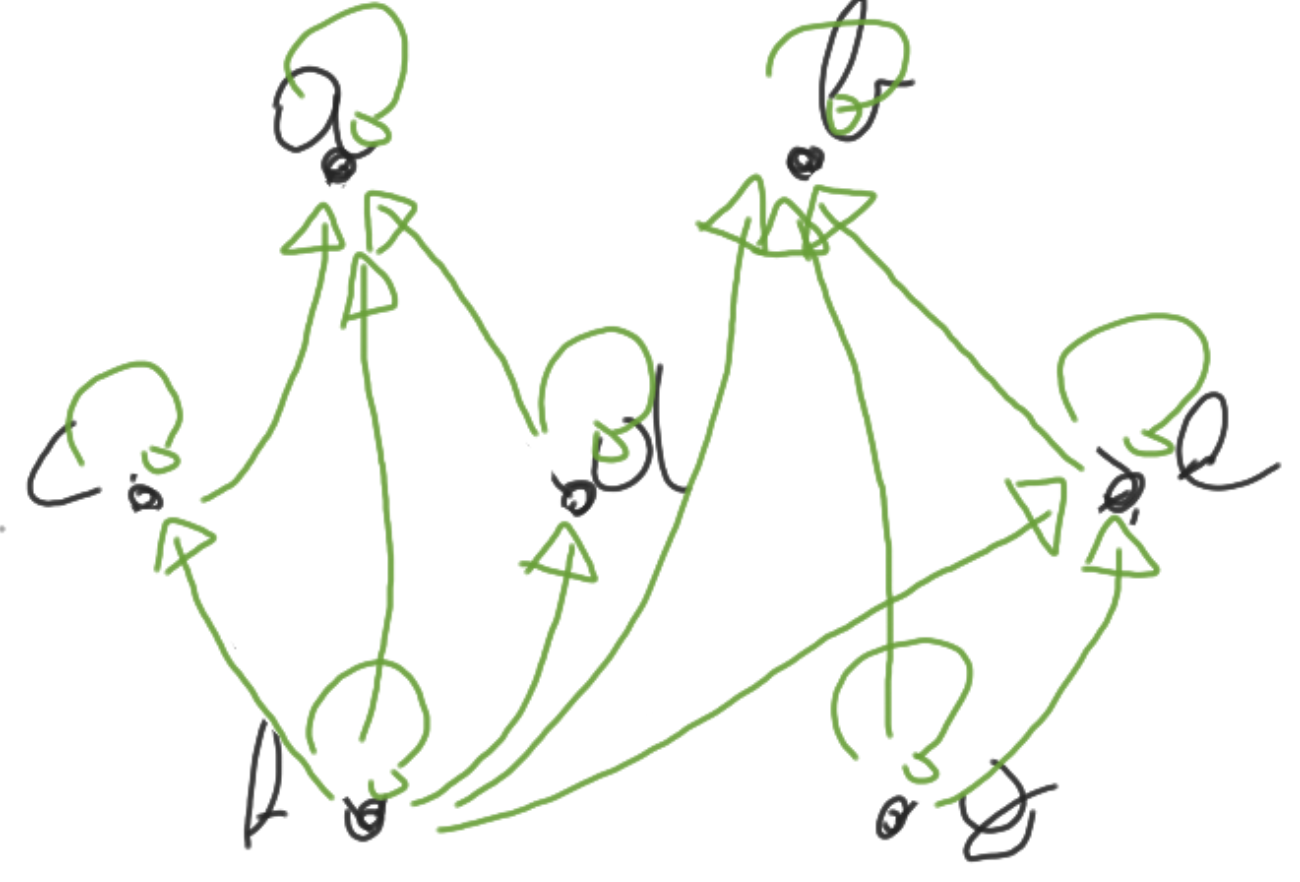
\( a \in A \) is een bovengrens voor \(X\): \(\forall x \in X: x \preceq a \)

\( a \in A \) is een ondergrens voor \(X \): \(\forall x \in X: a \preceq x \)

Basisconcepten

het supremum van X: de kleinste bovengrens voor X 

Het infimum van X: de grootste ondergrens voor X 

Basisconcepten

Een complete tralie elke eindige verzameling \( X \subseteq A \) heeft een supremum en infimum

Een quasi-orde is reflexief en transitief

Oefening 7.3

Gegeven R is symmetrisch en anti-symmetrisch

\( \forall x,y \in A: (x,y) \in R \Leftrightarrow (y,x) \in R \) 

\( \forall x,y \in A: (x,y) \in R \wedge (y,x) \in R \Rightarrow x = y \) 

Te bewijzen \( \forall (x,y) \in R: x = y \)

• Stel \( \exist (x,y) \in R: x \neq y \)
• R is symmetrisch
  \( (x,y) \in R \Rightarrow (y,x) \in R \)
• R is anti-symmetrisch:
  \( (x,y) \in R \wedge (y,x) \in R \Rightarrow x = y \)
• In contradictie met onze aanname!

Oefening 7.4

Te bewijzen \(\Leftrightarrow \) is een equivalentierelatie

\( \forall x:x \Leftrightarrow x \) (triviaal)

\( \forall x,y: ( x \Leftrightarrow y ) \Leftrightarrow (y \Leftrightarrow x) \) (zie hoofdstuk 2)

\( \forall x,y,z: (x \Leftrightarrow y) \wedge (y \Leftrightarrow x) \Rightarrow (x \Leftrightarrow z) \) (zie hoofdstuk 2)

Equivalentierelatie is reflexief, symmetrisch en transitief

Te bewijzen

Oefening 7.6

Gegeven \( y_1, y_2 \in K(x) \)

Te bewijzen \( y_1 \sim y_2 \)

• definitie equivalentieklasse:
  \(y_1 \in K(x) \Rightarrow y_1 \sim x \)
  \( y_2 \in K(x) \Rightarrow y_2 \sim x \)
• \( \sim\) is een symmetrisch:
  \( y_2 \sim x \Rightarrow x \sim y_2 \)
• \( \sim \) is transitief:
  \( y_1 \sim x \wedge x \sim y_2 \Rightarrow y_1 \sim y_2 \)

Oefening 7.15

Beschouw \( A,\subseteq \) met \(A = \mathcal{P}(U) \)

Gevraagd Wat zijn \(sup(\emptyset ) \) en \(inf (\emptyset ) \)

• \( a \in A \) is een bovengrens \( \forall x \in X: x \preceq a \)
• \( a \in A \) is een bovengrens \( \forall x \in \emptyset: x \preceq a \) 
• Dus elk element uit A is een bovengrens
  (analoog voor een ondergrens)
• \( sup( \emptyset) = \emptyset \) 
• \( inf( \emptyset ) = U \)

Oefening 7.15 extra

Beschouw \( A,\subseteq \) met \(A = \mathcal{P}(U) \)

Gevraagd Wat zijn \(sup( \{\emptyset \}) \) en \(inf ( \{\emptyset\} ) \)

• \( a \in A \) is een bovengrens \( \forall x \in X: x \preceq a \)
• \( a \in A \) is een bovengrens \( \forall x \in \{\emptyset\}: x \subseteq a \) 
• Dus elke verzameling \(B\) waarvoor geldt \( \emptyset \subseteq B \) is een bovengrens
• Dus alle verzamelingen in \( \mathcal{P}(U) \) zijn een bovengrens
• \( sup( \{\emptyset\}) = \emptyset \) 
• Elke verzameling \( B \) waarvoor geldt \( B \subseteq \emptyset \) is een ondergrens
• Dat is alleen de lege verzameling zelf
• \( inf (\{\emptyset \} ) = \emptyset \)