Local replacement and

Partition into Triangles

Overview

Theory of NP-Completeness
Problem
Theorem
Proof

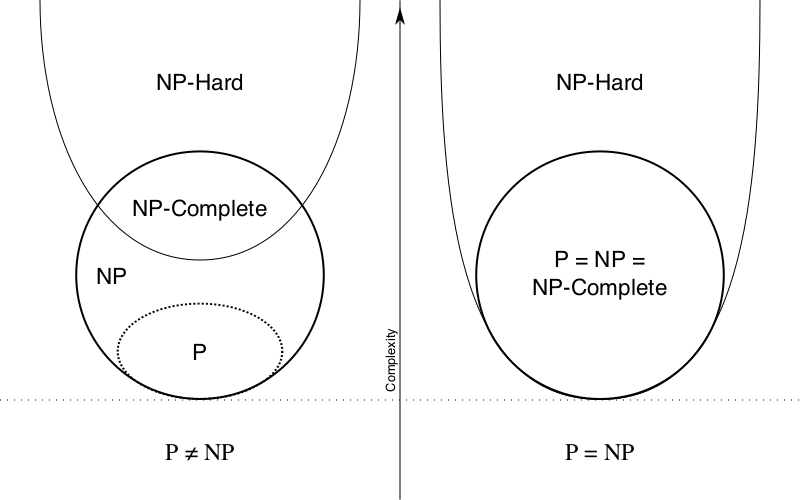
Theory of NP-Completeness

Definitions:

P - deterministic polynomial-time decision problems
NP - non-deterministic turing machine problems that can be verified in polynomial-time.
NP-Hard - at least as hard as the hardest problems in NP.

Theory of NP-Completeness

NP-Complete:

A decision problem D is
NP-complete if:
- D is in NP, and
- Every problem in NP is reducible to D in polynomial time

Problem

Instance:

A Graph G = (V,E) with |V| = 3q for a positive integer q.

Question:

Is there a partition of V into q disjoint sets v₁, v₂, ... , v_q of three vertices each, such that, for each V_i = {V_i[1], V_i[2], V_i[3]}, the three edges:

{V_i[1], V_i[2]},

{V_i[1], V_i[3]},

{V_i[2], V_i[3]},

all belong to E ?

Theorem

Intuition:

Clearly Partition into Triangles is in NP because we can first non-deterministically guess a partition of V and then check (in deterministic polynomial time) that each V_i fulfills the triangle condition.

Theorem:

Partition into Triangles is NP-Complete.

Proof

Approach:

We transform Exact Cover by 3-Sets to Partition into Triangles

Polynomial time transformation using local replacement.

Local Replacement:

Pick some aspect of the know NP-Complete problem instance to make up a collection of basic units.
We obtain the corresponding instance of the target problem by replacing each basic unit in a uniform way with a different structure.
The key point is that each replacement constituted only local modification of structure.

Proof

Let the set X with |X| = 3q and the collection C of 3 element subsets of X be an arbitrary instance of Exact Cover by 3 Sets.

We shall construct a graph G=(V,E), with |V|=3q', such that the desired partition exists for G if and only if C contains exact cover.

Proof:

Proof

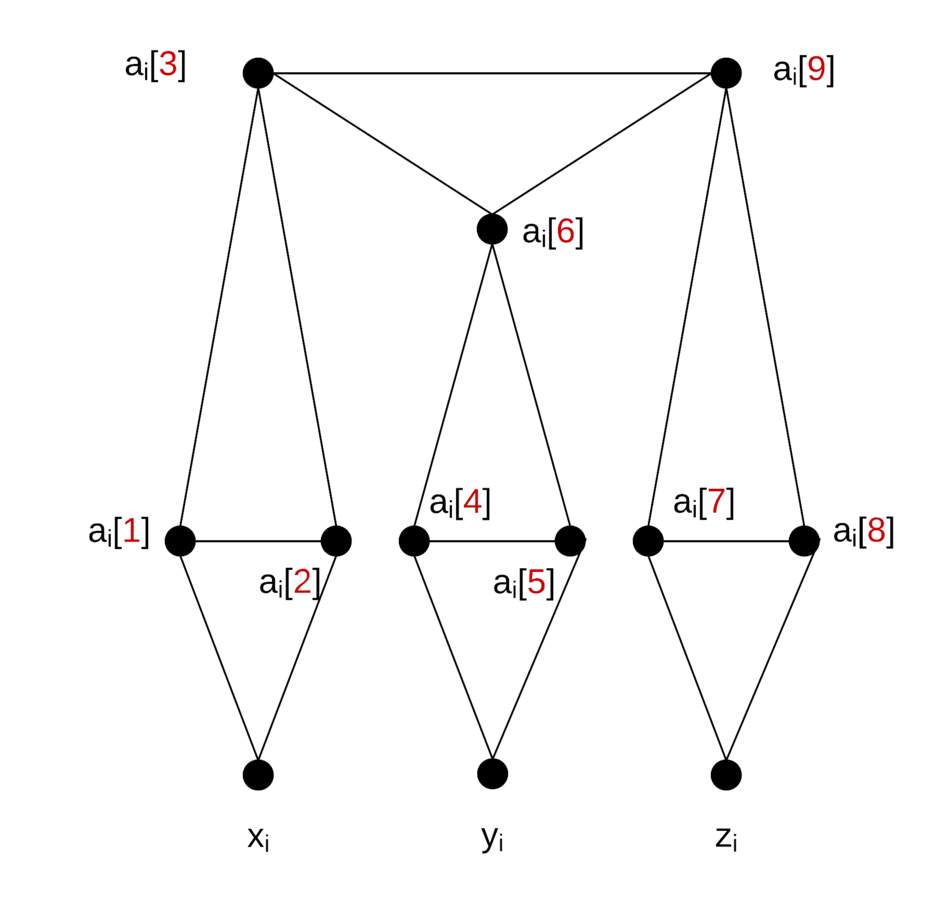
The basic units of the Exact Cover by 3 Sets instance are the 3-element subsets in C.

The local replacement substitutes for each such subset c_i = { x_i, y_i, z_i} ∈ C the collection E_i of 18 edges shown in the figure below:

Proof:

Proof

The only vertices that appear in edges belonging to more than a single E_i are those that are in the set X.

|V| = |X| + 9 |C| = 3q + 9 |C| so that q' = q + 3 |C| and is therefore an instance of Partition into Triangles.

Proof:

Proof

If c₁, c₂, ... , c_q are the 3 element subsets from C in any EXACT COVER for X, then the corresponding partition V = V1 U V2 U ... U Vq' is given by taking

{a_i[1], a_i[2], x_i}, {a_i[4], a_i[5], y_i}

{a_i[7], a_i[8], z_i}, {a_i[3], a_i[6], a_i[9] }

from the vertices meeting E_i wherever c_i = { x_i, y_i, z_i} IS in the exact cover, and by taking:

{a_i[3], a_i[6], a_i[9]}, {a_i[3], a_i[6], a_i[9]}, {a_i[3], a_i[6], a_i[9]}

from the vertices meeting E_i whenever c_i IS NOT in the exact cover.

Proof:

Proof

Let us say that it was {a_i[1], a_i[2], x_i}
Then {a_i[4], a_i[5], y_i}{a_i[7], a_i[8], z_i}, and {a_i[3], a_i[6], a_i[9] }

must also be in the triangle partition.

Proof:

Proof

Therefore each x appears in exactly one chosen c_i

Proof:

This also implies that we choose exactly q c_i elements of C.

We have shown that G can be partitioned into
q' = q + |C| triangles if and only if C contains an exact cover of q sets for X.