Bloom filters
And Other Probabilistic Data Structure Friends
the url filtering problem
- We have a list of URLs known to be malicious, but it's huge - let's say 100 MB
- Checking a URL against everything in that list would take obnoxiously long ("but there's a way around that" - hold that thought!)
- Heck, even just downloading the 100 MB list would be kinda gross :(
- But querying google's IsThisWebsiteMalicious service on every URL is obviously not good...
BLOOM FILTERS
- Relax the problem constraints - what if a query can return "no" or "maybe"?
- Hash each value with N hash functions
- For practical purposes, can cheat w/ just 1 underlying hash
- Insert!
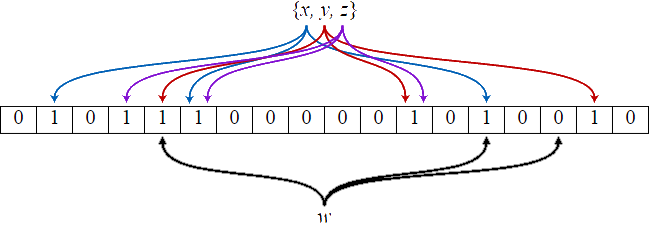
bloom filters cont'd
- Tradeoff between false positive rate and size of underlying bit array - 1% error rate requires only around 9.6 bits per element, 0.1% error rate only needs 4.8 more
- add, test both constant-time unlike any other constant-space set data structure
- Never 'fills up', just reports more false pos
uses
- Cache filtering for content delivery networks - avoid caching one-hit wonders
- Aforementioned browser malicious URL detection - only double-check on a hit
- 'molecular fingerprints' used to search huge databases of chemical structures
- Can be extended to allow for removing items from the filter
the count distinct problem
-
Find the number of distinct elements in a datastream where elements repeat
-
i.e. IP addresses passing through a router, unique visitors to website
-
Naive solution does not scale in memory terribly well
Hyper log log
-
Try to estimate # of times coin was flipped by length of longest run of heads or tails
-
Hash the incoming data, look for runs
-
Bucket many estimates, take harmonic mean of the results
-
First N bits of hash determine bucket
-
i.e. 01001001011000101 -> bucket 5, run of 3 zeroes = if buckets[5] < 4, buckets[5] = 4