Distance Evolutions in

Preferential Attachment Models

Joost Jorritsma  

joint with Júlia Komjáthy

 

(Random Struct. & Alg. '20, Ann. of Applied Probability '22)

Seminario Probabilidades de Chile

December 2022

tiny.cc/DistanceEvolutionPAM

Guiding 'real-world' example

Internet network: communicating routers and servers

~1969: 2 connected sites  (UCLA, SRI)

Time

~1971: 15 connected sites

~1989: 0.5 million users

~2020: billions of                              connected devices

  • Evolving/dynamic network:
    • Vertices arrive over time.
    • Connect to present vertices.
    • (Nodes may be removed or replaced.)
    • (Edges between 'old' vertices are removed or placed.)
  • [Faloutsos, Faloutsos & Faloutsos, '99]:
    • # connections per router decays as power-law: \(p_k\sim k^{-\tau}, \tau>2\).
    • Short average hopcount between routers.

Guiding 'real-world' example

Internet network: communicating routers and servers

  • Evolving network: Vertices arrive over time, connect to present vertices.
  • [Faloutsos, Faloutsos & Faloutsos, '99]: Short average hopcount.

1999

\(\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4\)

2005

\(\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3\)

2022

\(\mathrm{dist}_{{\color{red}'22}}(u_{'99}, v_{'99}) = 2\)

  • How does hopcount between old nodes change in growing network?

\(u_{'99}\)

\(v_{'99}\)

Preferential attachment models

Definition

  • Start with a single vertex
  • Vertices enter one-by-one at times \(t=2, 3,...\).
  • New vertex prefers connection to high-degree vertex:
    • Fixed outdegree: \((m,\delta): m\) edges/new vertex (\(\delta>-m\)):
      $$\mathbb{P}\big(v_{t+1} \overset{j}{\longrightarrow} v_i\big) \propto \mathrm{deg}_{t,j}(v_i) + \delta/m.$$
    • Variable outdegree: \(\forall v_i \in \mathrm{PA}_t\), independently, (\(\gamma,\eta\in(0,1)\))
      $$\mathbb{P}\big(v_{t+1} \longrightarrow v_i\big) = (\gamma \mathrm{deg}_{t}(v_i)+\eta)/t.$$
  • Animation

Thm. [Bollobás, Riordan, Spencer, Tusnády '01; Dereich, Mörters '09]

Limiting degree distribution decays as power-law: for \(\tau_{m,\delta}=3+\delta/m;  \tau_\gamma=1+1/\gamma\),

$$p_k \sim k^{-\tau}.$$

Many dependencies:

New edges at time \(t\) depend on earlier edges, influences edges at \(t'>t\).

Distances on PAMs

Thm. [Dereich, Mönch, Mörters '12].

For \(\tau\in(2,3)\),  \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\):

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) \asymp  4\frac{\log\log(t)}{|\log(\tau-2)|} $$

 

Thm. [Dommers, v/d Hofstad, Hooghiemstra '10].

For \(\tau>3\), \(\exists c_1, c_2>0\):

$$c_1\preccurlyeq\frac{\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})}{\log(t)} \preccurlyeq c_2.$$

Thm. [Bollobás, Riordan '04; Dereich, Mönch, Mörters '17].

For \(\tau=3\):

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})\asymp \frac{\log(t)}{\log\log(t)}.$$

Thm. [Dereich, Mönch, Mörters '12; J., Komjáthy '20].

For \(\tau\in(2,3)\),  \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\):

$$\Bigg(\left|\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) - 4\frac{\log\log(t)}{|\log(\tau-2)|}\right|\Bigg)_{t\ge 0} $$

is a tight sequence of random variables (\(\forall \varepsilon>0 \exists M(\varepsilon)\forall t: \mathbb{P}(|Y_t|\ge M)<\varepsilon\)).

Static properties in PAMs

  • Examples
    • Degree distribution.
    • Typical distance.
    • Diameter.
    • Local neighborhood of a typical vertex (local limit).
    • Component sizes.
       

  • Comparison to static (non-growing) models
    (configuration model, rank-1 inhomogeneous random graph, ...).
     

  • Results don't display dynamics in PAMs (contrary to proofs).

    • Exception: degree evolution \((\mathrm{deg}_{t'}(v))_{t'\ge v}\) of fixed vertices.

Goal: understand how the graph evolves from perspective of graph at time \(t\)

Main Question

Consider \(\Big(\big(\mathrm{dist}_{{\color{red}t'}}(U_{\color{blue} t}, V_{\color{blue} t})\big)_{{\color{red}t'}\ge {\color{blue}t}}\Big)_{t\ge 0}\) , and maximal deviation

$$X_t^f := \sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f({\color{blue}t}, {\color{red}t'})\right|.$$

Q1. For \(\tau\in(2,3)\), can we identify \(f_\tau(t, t')\) s.t.

       \((X_t^{f_\tau})_{t\ge 0}\) is a tight sequence?

\(\mathrm{dist}_{t_0}(U_{t_0}, V_{t_0}) = 7,\)

\(\mathrm{dist}_{t_1}(U_{t_0}, V_{t_0}) = 6,\)

\(0\)

\(t_2\)

\(\mathrm{dist}_{t_2}(U_{t_0}, V_{t_0}) = 2\)

\(U_{t_0}\)

\(V_{t_0}\)

\(t_1\)

\(t_0\)

Q2. For \(\tau\in(2,3)\), identify \(f_\tau(t, t')\) s.t.

$$\Bigg(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Bigg)_{t\ge 0}$$         is a tight sequence.

Main Theorem

Thm. [J., Komjáthy, '22].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Corollary. Hydrodynamic limit [J., Komjáthy '22].
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$f_\tau(t,T_t(a)) = 4(1-a)\frac{\log\log(t)}{|\log(\tau-2)|}\vee 2,$$ and

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Main Theorem

Corollary. Hydrodynamic limit [J., Komjáthy '22].
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Back to static: weighted distance

Theorem. [J., Komjáthy, '22]. Let

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Then, for \(\tau\in(2,3)\), the following sequence is tight:

$$\left(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\right)_{t\ge 0}$$  

Corollary (Static). For \(\tau\in(2,3)\), the following sequence is tight:

$$\left| \mathrm{dist}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 0}$$  

Weighted distance: \(d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e\)

Def. Fix non-negative random variable \(L\). Upon arrival

        edge \(e\), assign i.i.d. copy \(L_e\).

 

Weighted distance: a game

Corollary. For \(\tau\in(2,3)\), the following sequence is tight:

$$\left| \mathrm{dist}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}$$  

Weighted distance: \(d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e\)

Def. Fix non-negative random variable \(L\). Upon arrival

        of edge \(e\), assign i.i.d. copy \(L_e\).

 

\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - 8\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
  • \(L\equiv 2\): the following sequence is tight:

     
  • \(L\equiv \mathrm{Unif}[1,3]\): the following sequence is tight:
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - ??\phantom{\frac{\log\log(t)}{|\log(\tau-2)|} }\right|_{t\ge 1}
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - ??\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

Weighted distance: a game

\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - 8\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
  • \(L\equiv 2\): the following sequence is tight:

     
  • \(L\sim \mathrm{Unif}[1,3]\): the following sequence is tight:

     
  • \(L\sim 1+\mathrm{Exp(\lambda)}\): the following sequence is tight:

     
  • \(L\sim\mathrm{Exp}(\lambda)\): the following sequence is tight:
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - ??\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}
\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - \phantom{4\frac{\log\log(t)}{|\log(\tau-2)|} }\right|_{t\ge 1}

Explosive weights

  • \(L\sim\mathrm{Exp}(\lambda)\): the following sequence is tight:
\big(\mathrm{dist}^{(L)}_t(U_t, V_t)\big)_{t\ge 1}
  • We identify \(\beta=\beta(L)\), with \(\mathbb{P}(\beta<\infty)=1\) s.t. as \(t\to\infty\)
\mathrm{dist}^{(L)}_t(U_t, V_t)\overset{\mathrm{d}}\longrightarrow\beta.
  • Explosion occurs if and only if \(\tau\in(2,3)\), and \(F_L\) satisfies
\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty.
  • Examples: \(\mathrm{Exp}(\lambda), \mathrm{Unif[0,\lambda]}, \mathcal{N}(0,1)^2, ...\)

Conservative weights

  • Explosion occurs if and only if \(\tau\in(2,3)\), and \(F_L\) satisfies
\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty.
  • Otherwise, \(L\) is conservative, and we show that (for almost all such \(L\))
\left(d^{(L)}_t(U_t, V_t) - 2\sum_{k=1}^{f_\tau(t,t)/2}F_L^{(-1)}\left(\exp\big(-(\tau-2)^{-k/2}\big)\right)\right)_{t\ge 1}

is a tight sequence.

  • For any increasing function \(g=O(\log\log(t))\), there exists \(L_g\) s.t.
\left(d^{(L_g)}_t(U_t, V_t) - g(t)\right)_{t\ge 1}

is a tight sequence.

Explosion: Intuition

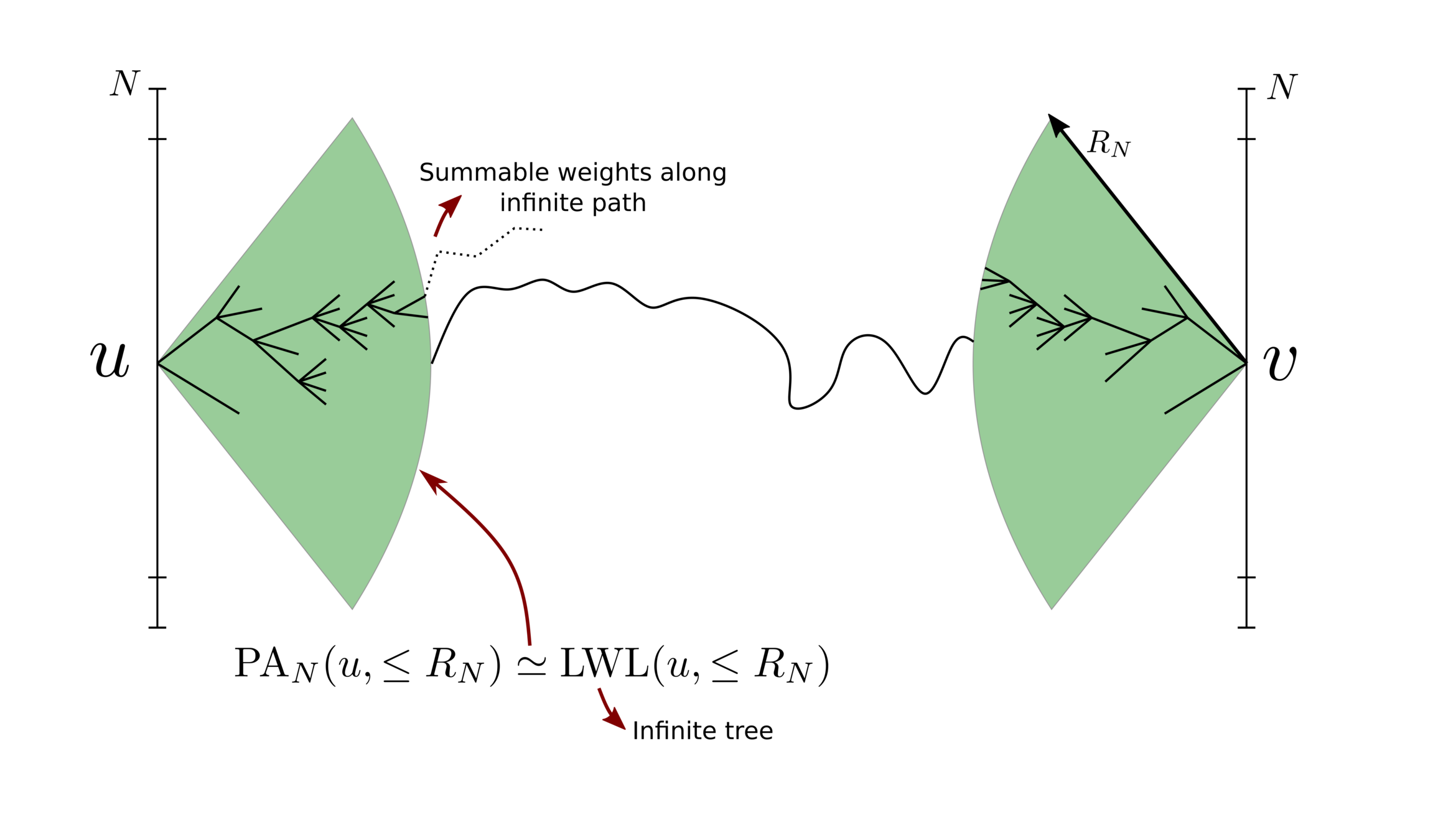
  • Summable minima in greedy path when small weights likely \(\beta>1\):

    $$F_L(x)\ge\exp\big(-\exp\big(x^{-\beta}\big)\big).$$

  • Doubly exponential ball growth iff \(\tau\in(2,3)\): no greedy path otherwise.

Convservative: Intuition

  • Control minima along greedy path/generations
  • Most of the weight in red segment
    (contrary to explosion)

Weighted-distance evolution

Weighted version (Evolution statement). [J., Komjáthy '22].
Let \(\tau\in(2,3)\), and pick conservative edge-weight distribution \(F_L\). Then,

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=f_\tau^{(1)}(t,t)-f_\tau^{(1)}(t,t')+1}^{f_\tau^{(1)}(t,t)}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k/2})\big),$$

and

 

 

 

f_\tau^{(1)}(t,t') = 2\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 1.

Graph-distance evolution: \(L\equiv 1\).

Heuristic upper bound

Statement. [J., Komjáthy '22].

For \(\tau\in(2,3)\),
$$ \mathbb{P}\Big(\forall t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon. $$

Weaker statement. [J., Komjáthy '22].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

"Proof" of statement by smart union bound.

  • Consider \((t_i(t))_{i\ge 0}\) at integer crossings rhs (i.e., event changes).
  • Distance is non-increasing.
  • By weak version, the statement follows if for \(t\) large \(\sum_i \varepsilon_{t_i(t)} \leq \varepsilon\).
  • Weak statement follows from minor adaptations of [Dommers, v/d Hofstad, Hooghiemstra '10; Dereich, Mönch, Mörters '12; Caravenna, Garavaglia, v/d Hofstad '19; J., Komjáthy '20].

Unfortunately \(\int_t^\infty \varepsilon_{t'} \mathrm{d}t'\to \infty.\)

Naive idea: Union bound.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, \(t'=t\):

\(^{(t)}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

bounded-length segments

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, \(t'=t\):

\(\mathrm{deg}_t(\cdot)\)

\(\mathrm{Core}(t)\)

  • \(\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}\).
  • If \(\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}\).
  • # of iterations to reach core: smallest \(k_t\) s.t.
    $$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t/\log(t)}.$$
  • \(k_t\approx\log\log(t)/|\log(\tau-2)|=\frac{1}{4}f_\tau(t,t)\) iterations for \(U_t, V_t\).

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 1, \(t'>t\):

\(\mathrm{deg}_t(\cdot)\)

\(\mathrm{Core}(t)\)

\(\mathrm{deg}_{t'}(\cdot)\)

\(\mathrm{Core}(t')\)

  • \(\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}\).
  • If \(\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}\).
  • # of iterations to reach core : smallest \(k_{t'}\) s.t.
    $$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t'/\log(t')}.$$
  • Competing effects:
    (1) Core threshold increases;
    (2) degree increases.
  • Strong control of \(\text{deg}_{t'}(q_{t,0})\):
    Using Móri-martingale, Doob's maximal inequality:
    \(\text{deg}_{t'}(q_{t,0})\gtrsim (t'/t)^{1/(\tau-1)}\) for all \(t'>t\)     .
  • \(k_{t'}\le \frac{1}{4}f_\tau(t,t')\).
  • If \(t'=T_t(a)\), # iterations is linear in \(a\)

Heuristic lower bound

Statement. [J., Komjáthy '22]. For \(t\) large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

2. Bound rhs using 'old' methods [Dereich, Mönch, Mörters '12].

Naive guess (similar to upper bound):

1. Find sequence \((t_i)_{i\ge 0}\) at which event changes. Then

$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \sum_i \mathbb{P}\Big(\mathrm{dist}_{t_i}(U_t, V_t)\le f_\tau(t,t_i)-1/\varepsilon\Big).$$

RHS not summable, new machinery needed

Heuristic lower bound

Statement. [J., Komjáthy '22]. For \(t\) large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For \(t\) sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

\(\leq C/(t'\log^3(t'))\)

Let \(\mathcal{E}(t,t'):= \{\mathrm{dist}_{t'}(U_t, V_t)\ge f_\tau(t,t')-1/\varepsilon\}\). Then

\(\mathbb{P}\Big(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \Big)\le\mathbb{P}\big(\)there is a short path that traverses \(t'\big)\)

Main idea: Time-dependencies in the growing graph

There is a first time of failure: \(f_\tau(t,t') \searrow\).

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) = \mathbb{P}\big(\neg \mathcal{E}(t,t)\big) + \sum_{t'=t+1}^\infty\mathbb{P}\bigg(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \bigg)$$

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \varepsilon + \sum_{t'=t+1}^\infty C/(t'\log^3(t')) \overset{t\to\infty}\longrightarrow \varepsilon$$

\(\vdots\)

computations,

inductive proves, etc ...

Q2. For \(\tau\in(2,3)\), identify \(f_\tau(t, t')\) s.t.

$$\Bigg(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Bigg)_{t\ge 0}$$         is a tight sequence.

Solves main question

Thm. [J., Komjáthy, '22].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Weighted distances.
Control added weight added in each iteration.

Open questions

  • Other evolving properties 
    • triangles
    • colorings
    • distance when \(\tau>3\) (even static case open)

       
  • # edges on shortest \(L\)-path if \(\sup\{x: F_L(x)>0\}=0\)
    • ?? logarithmic if \(L\) explosive ??
  • fluctuations around main terms

Thank you!

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, \(t'=t\):

\(^{(t)}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

bounded-length segments

Weighted distance evolution

Weighted version (Evolution statement). [J., Komjáthy '22].
Let \(\tau\in(2,3)\), and pick conservative edge-weight distribution \(F_L\). Then,

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=f_\tau^{(1)}(t,t)-f_\tau(t,t')+1}^{f_\tau(t,t)}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k/2})\big),$$

and

 

f_\tau(t,t') = 2\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 1.

Intuition

  • Two consecutive terms correspond to minimal weight added in one iteration of the upper bound.
  • Let \(X_1,\dots, X_n\) be i.i.d. random variables. Then $$\min\{X_1,\dots,X_n\}\approx F_L^{(-1)}(1/n).$$
  • Graph distance drops: largest term removed from sum.

Distance Evolutions in

Preferential Attachment Models

Joost Jorritsma  

joint with Júlia Komjáthy

 

(Random Struct. & Alg. '20, Ann. of Applied Probability '22+)

MiSe ETH Zürich

March 2022

arXiv: tiny.cc/DistanceEvolutionPAM

Guiding 'real-world' example

Internet network: communicating routers and servers

~1969: 2 connected sites  (UCLA, SRI)

Time

~1971: 15 connected sites

~1989: 0.5 million users

~2020: billions of                              connected devices

  • Evolving/dynamic network:
    • Vertices arrive over time.
    • Connect to present vertices.
    • (Nodes may be removed or replaced.)
    • (Edges between 'old' vertices are removed or placed.)
  • [Faloutsos, Faloutsos & Faloutsos, '99]:
    • # connections per router decays as power-law: \(p_k\sim k^{-\tau}, \tau>2\).
    • Short average hopcount between routers.

Guiding 'real-world' example

Internet network: communicating routers and servers

  • Evolving network: Vertices arrive over time, connect to present vertices.
  • [Faloutsos, Faloutsos & Faloutsos, '99]: Short average hopcount.

1999

\(\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4\)

2005

\(\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3\)

2022

\(\mathrm{dist}_{{\color{red}'22}}(u_{'99}, v_{'99}) = 2\)

  • How does hopcount between old nodes change in growing network?

\(u_{'99}\)

\(v_{'99}\)

Preferential attachment models

Definition

  • Start with a single vertex
  • Vertices enter the network one-by-one at discrete (time-)steps \(t=2, 3,...\).
  • New vertex connects to old vertices according to some increasing function of the degree:
    • Fixed outdegree: \((m,\delta): m\) edges/new vertex (\(\delta>-m\)):
      $$\mathbb{P}\big(v_{t+1} \overset{j}{\longrightarrow} v_i\big) \propto \mathrm{deg}_{t,j}(v_i) + \delta/m.$$
    • Variable outdegree: \(\forall v_i \in \mathrm{PA}_t\), independently, (\(\gamma,\eta\in(0,1)\))
      $$\mathbb{P}\big(v_{t+1} \longrightarrow v_i\big) = (\gamma \mathrm{deg}_{t}(v_i)+\eta)/t.$$
  • Animation

Many dependencies:

Edge added at time \(t\) depends on earlier edges, influences later added edges

Thm. [Bollobás, Riordan, Spencer, Tusnády '01; Dereich, Mörters '09]

Limiting degree distribution decays as power-law: for \(\tau_{m,\delta}=3+\delta/m;  \tau_\gamma=1+1/\gamma\),

$$p_k \sim k^{-\tau}.$$

Distances on PAMs

Thm. [Dereich, Mönch, Mörters '12].

For \(\tau\in(2,3)\),  \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\):

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) \asymp  4\frac{\log\log(t)}{|\log(\tau-2)|} $$

 

Thm. [Dommers, v/d Hofstad, Hooghiemstra '10].

For \(\tau>3\), \(\exists c_1, c_2>0\):

$$c_1\preccurlyeq\frac{\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})}{\log(t)} \preccurlyeq c_2.$$

Thm. [Bollobás, Riordan '04; Dereich, Mönch, Mörters '17].

For \(\tau=3\):

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})\asymp \frac{\log(t)}{\log\log(t)}.$$

Thm. [Dereich, Mönch, Mörters '12; J., Komjáthy '20].

For \(\tau\in(2,3)\),  \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\):

$$\bigg(\left|\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) - 4\frac{\log\log(t)}{|\log(\tau-2)|}\right|\bigg)_{t\ge 0} $$

is a tight sequence of random variables (\(\forall \varepsilon>0 \exists M(\varepsilon)\forall t: \mathbb{P}(|Y_t|\ge M)<\varepsilon\)).

Literature perspective on PAMs

  • Many static/limiting properties are well-understood
    • Degree distribution.
    • Typical graph distance.
    • Diameter of the graph.
    • Local neighborhood of a typical vertex (local weak sense).
    • Component sizes.
    • ...
    • ...

  • Studying static properties allows for comparison to static (non-growing) models (configuration model, Norros-Reittu, ...).

  • Theorem statements do not display dynamics inherently present in PAMs (contrary to proofs).

    • Exception: degree evolution \((\mathrm{deg}_{t'}(v))_{t'\ge v}\) of (sets of) fixed vertices.

Goal: try to understand how the graph evolves for \(t'\ge t\) from perspective of graph at time \(t\)

Main Question

Consider \(\Big(\big(\mathrm{dist}_{{\color{red}t'}}(U_{\color{blue} t}, V_{\color{blue} t})\big)_{{\color{red}t'}\ge {\color{blue}t}}\Big)_{t\ge 0}\) and define for a function \(f(t,t')\)

$$X_t^f := \sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f(t, t')\right|.$$

Q1. For \(\tau\in(2,3)\), can we identify \(f_\tau(t, t')\) s.t.

       \((X_t^{f_\tau})_{t\ge 0}\) is a tight sequence?

\(\mathrm{dist}_{t_0}(U_{t_0}, V_{t_0}) = 7,\)

\(\mathrm{dist}_{t_1}(U_{t_0}, V_{t_0}) = 6,\)

\(0\)

\(t_2\)

\(\mathrm{dist}_{t_2}(U_{t_0}, V_{t_0}) = 2\)

\(U_{t_0}\)

\(V_{t_0}\)

\(t_1\)

\(t_0\)

Q2. For \(\tau\in(2,3)\), identify \(f_\tau(t, t')\) s.t.

$$\Big(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Big)_{t\ge 0}$$         is a tight sequence.

Main Theorem

Thm. [J., Komjáthy, '22+].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Corollary. Hydrodynamic limit [J., Komjáthy '22+].
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$f_\tau(t,T_t(a)) = 4(1-a)\frac{\log\log(t)}{|\log(\tau-2)|}\vee 2,$$ and

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Main Theorem

Corollary. Hydrodynamic limit [J., Komjáthy '22+].
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Heuristic upper bound

Statement. [J., Komjáthy '22+].

For \(\tau\in(2,3)\),
$$ \mathbb{P}\Big(\forall t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon. $$

Weaker statement. [J., Komjáthy '22+].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

"Proof" of statement by smart union bound.

  • Consider \((t_i(t))_{i\ge 0}\) at integer crossings rhs (i.e., event changes).
  • Distance is non-increasing.
  • By weak version, the statement follows if for \(t\) large \(\sum_i \varepsilon_{t_i(t)} \leq \varepsilon\).
  • Weak statement follows from minor adaptations of [Dommers, v/d Hofstad, Hooghiemstra '10; Dereich, Mönch, Mörters '12; Caravenna, Garavaglia, v/d Hofstad '19; J., Komjáthy '20].

Unfortunately \(\int_t^\infty \varepsilon_{t'} \mathrm{d}t'\to \infty.\)

Naive idea: Union bound.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, \(t'=t\):

\(^{(t)}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

\(^{(t')}\)

bounded-length segments

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, \(t'=t\):

\(\mathrm{deg}_t(\cdot)\)

\(\mathrm{Core}(t)\)

  • \(\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}\).
  • If \(\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}\).
  • # of iterations needed to reach core: smallest \(k_t\) s.t.
    $$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t/\log(t)}.$$
  • \(k_t\approx\log\log(t)/|\log(\tau-2)|=\frac{1}{4}f_\tau(t,t)\) iterations for \(U_t, V_t\).

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For \(t\) large, there \(\exist\) nice \(t'\mapsto\varepsilon_{t'}\)

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 1, \(t'>t\):

\(\mathrm{deg}_t(\cdot)\)

\(\mathrm{Core}(t)\)

\(\mathrm{deg}_{t'}(\cdot)\)

\(\mathrm{Core}(t')\)

  • \(\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}\).
  • If \(\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}\).
  • # of iterations needed: smallest \(k_{t'}\) s.t.
    $$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t'/\log(t')}.$$
  • Competing effects:
    (1) Core threshold increases;
    (2) degree increases.
  • Strong control of \(\text{deg}_{t'}(q_{t,0})\):
    Using Móri-martingale, Doob's maximal inequality:
    \(\text{deg}_{t'}(q_{t,0})\gtrsim (t'/t)^{1/(\tau-1)}\) for all \(t'>t\)     .
  • \(k_{t'}\le \frac{1}{4}f_\tau(t,t')\).
  • If \(t'=T_t(a)\), # iterations is linear in \(a\)

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For \(t\) sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

2. Bound rhs using 'old' methods [Dereich, Mönch, Mörters '12].

Naive guess (similar to upper bound):

1. Find sequence \((t_i)_{i\ge 0}\) at which event changes. Then

$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \sum_i \mathbb{P}\Big(\mathrm{dist}_{t_i}(U_t, V_t)\le f_\tau(t,t_i)-1/\varepsilon\Big).$$

RHS not summable, new machinery needed

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For \(t\) sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For \(t\) sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

*In fact, we need a more advanced separation of events (using good and bad paths, inspired by [Dereich, Mönch, Mörters '12]) that makes the decomposition more interlinked.

\(\leq^\ast C/(t'\log^3(t'))\)

Let* \(\mathcal{E}(t,t'):= \{\mathrm{dist}_{t'}(U_t, V_t)\ge f_\tau(t,t')-1/\varepsilon\}\). Recall \(f_\tau(t,t')\) is non-increasing. Then

\(\mathbb{P}\Big(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \Big)\le\mathbb{P}\big(\)there is a short path that traverses \(t'\big)\)

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) = \mathbb{P}\big(\neg \mathcal{E}(t,t)\big) + \sum_{t'=t+1}^\infty\mathbb{P}\bigg(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \bigg)$$

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \varepsilon + \sum_{t'=t+1}^\infty C/(t'\log^3(t')) \overset{t\to\infty}\longrightarrow \varepsilon$$

\(\vdots\)

computations,

inductive proves, etc ...

Weighted distance in PAM

Ex.: Many distributions with support starting at 0 are explosive: Unif[0,1], Exp(\(\lambda\)).

Threshold: \(L\) is explosive if close to 0 for some \(\beta>1\)

$$F_L(x)\ge\exp\big(-\exp\big(x^{-\beta}\big)\big).$$

Def. Weighted distance: \(d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e\)

Weighted version (Static statement). [J., Komjáthy '20].
Let \(\tau\in(2,3)\). Equip every edge with i.i.d. \(L_e\ge 0\) with cdf \(F_L\), \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\).

If \(F_L\) satisfies

$$\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty,$$

then \(d_t^{(L)}(U_t, V_t)\to \beta^{(1)}+ \beta^{(2)}\), with \(\mathbb{P}(\beta^{(i)}<\infty)=1\).

Otherwise, if \(L\) is not too flat, then we identify \(f^{(L)}_\tau(t,t)\) such that $$\Big(d_t^{(L)}(U_t, V_t)-f^{(L)}_\tau(t,t)\Big)_{t\ge 0}$$ is a tight sequence.

Main theorem (general version)

Weighted version (Evolution statement). [J., Komjáthy '20+].
Let \(\tau\in(2,3)\). Equip every edge with i.i.d. \(L_e\ge 0\), \(U_t, V_t\sim \text{Unif(Largest cluster}(t))\). If \(F_L^{(-1)}\) is not extremely flat, then

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=(f_\tau(t,t)-f_\tau(t,t'))/4}^{(f_\tau(t,t))/4}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k})\big).$$

Def. Weighted distance: \(d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e\)

Intuition

  • Every term corresponds to minimal weight added in one iteration.
  • Let \(X_1,\dots, X_n\) be i.i.d. random variables. Then $$\min\{X_1,\dots,X_n\}\approx F_L^{(-1)}(1/n).$$
  • Graph distance drops: largest term removed from sum.
Made with Slides.com