Largest component in spatial inhomogeneous random graphs

Large deviations of the giant in spatial random graphs

Joost Jorritsma

joint with Júlia Komjáthy, Dieter Mitsche

Long-range phenomena in percolation, September '24

Supercritical bond percolation on $\mathbb{Z}^d$

\mathbb{P}\big(k< |{\color{green}\mathcal{C}(0)}|<\infty\big)\sim

\exp\big(-\Theta(k^{\mathbf{\zeta}})\big)

[Gandolfi '88, Grimmett & Marstrand '90, Kesten & Zhang '90, Pisztora '96]

|{\color{red}\mathcal{C}_n^{(2)}}|\sim_\mathbb{P}(\log n)^{1/\zeta}

Surface-tension driven behavior

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)\sim

\exp\big(-\Theta(n^{\mathbf{\zeta}})\big)

\theta(p):=\mathbb{P}(0\leftrightarrow \infty)>0

\zeta=\frac{d-1}d

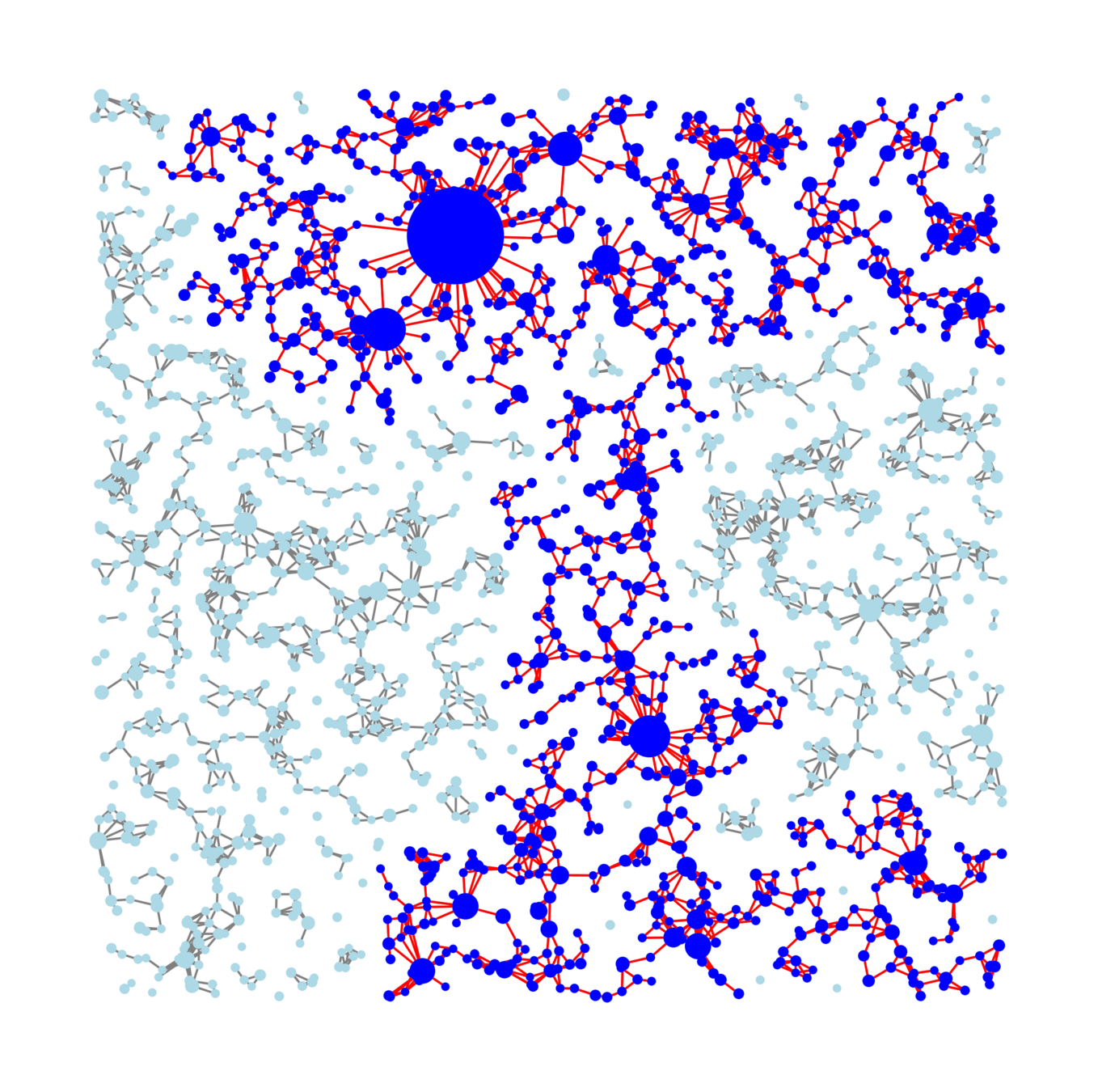
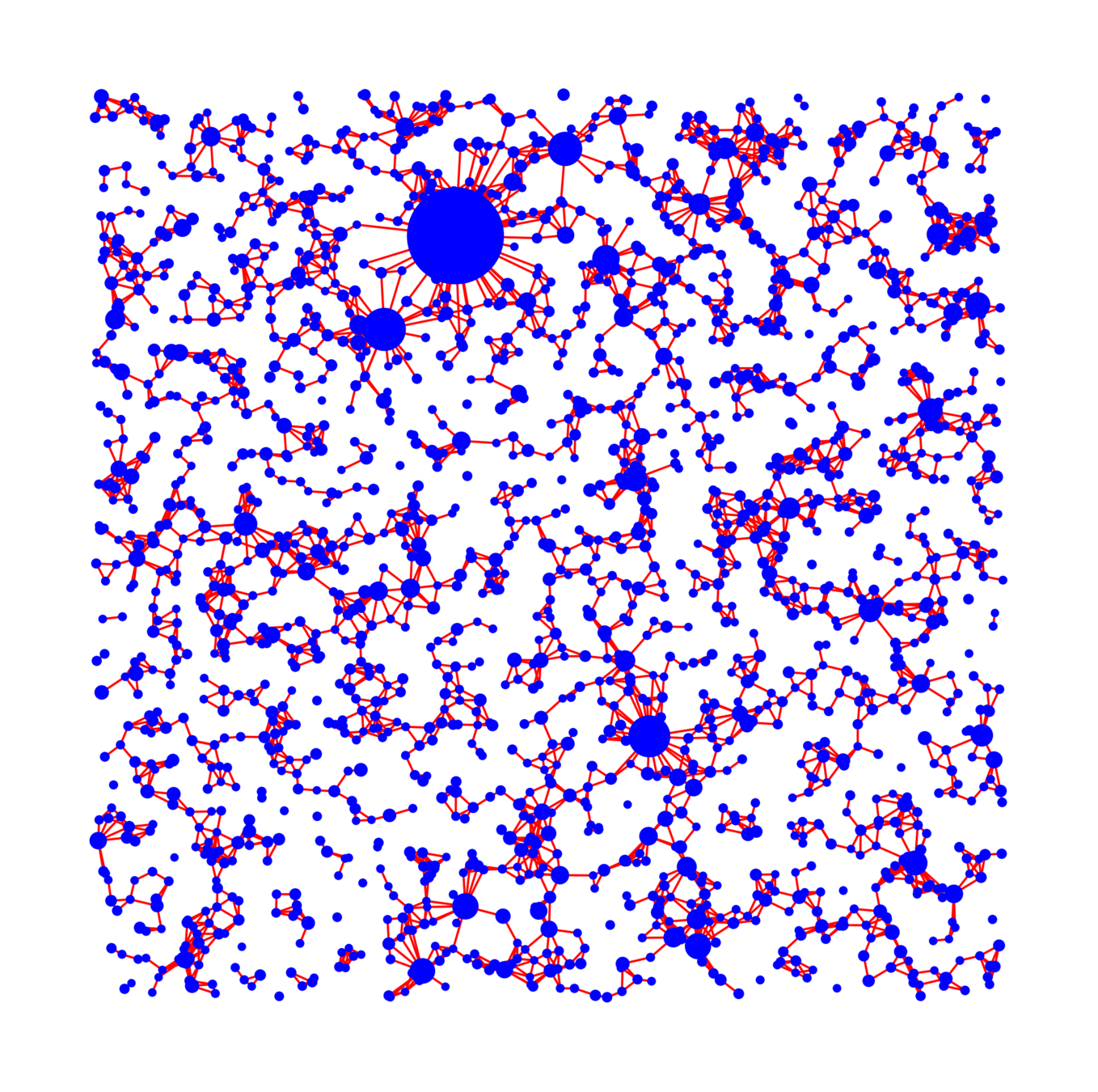
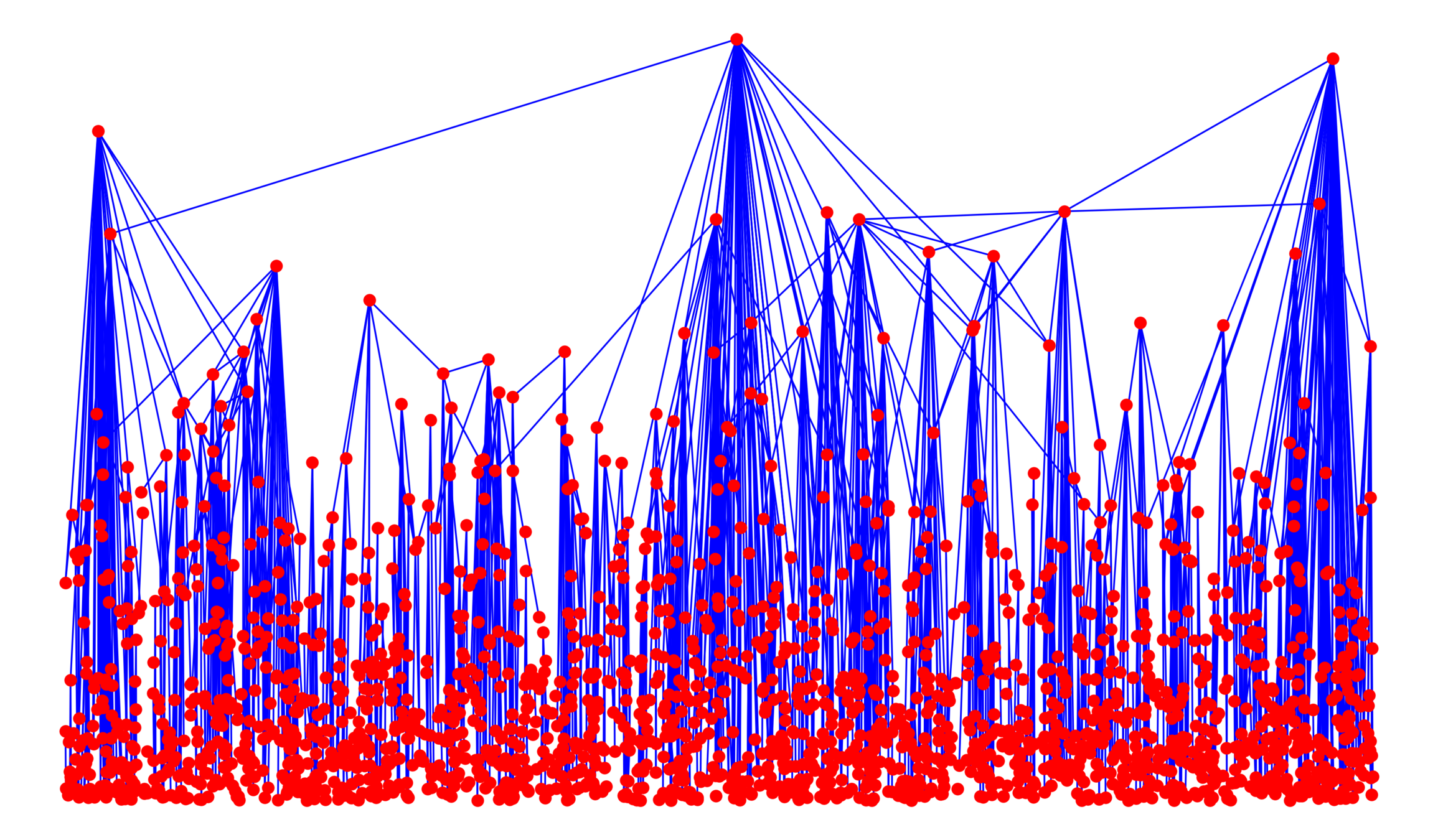
The largest component

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)\sim

\exp\big(-\Theta(n)\big)

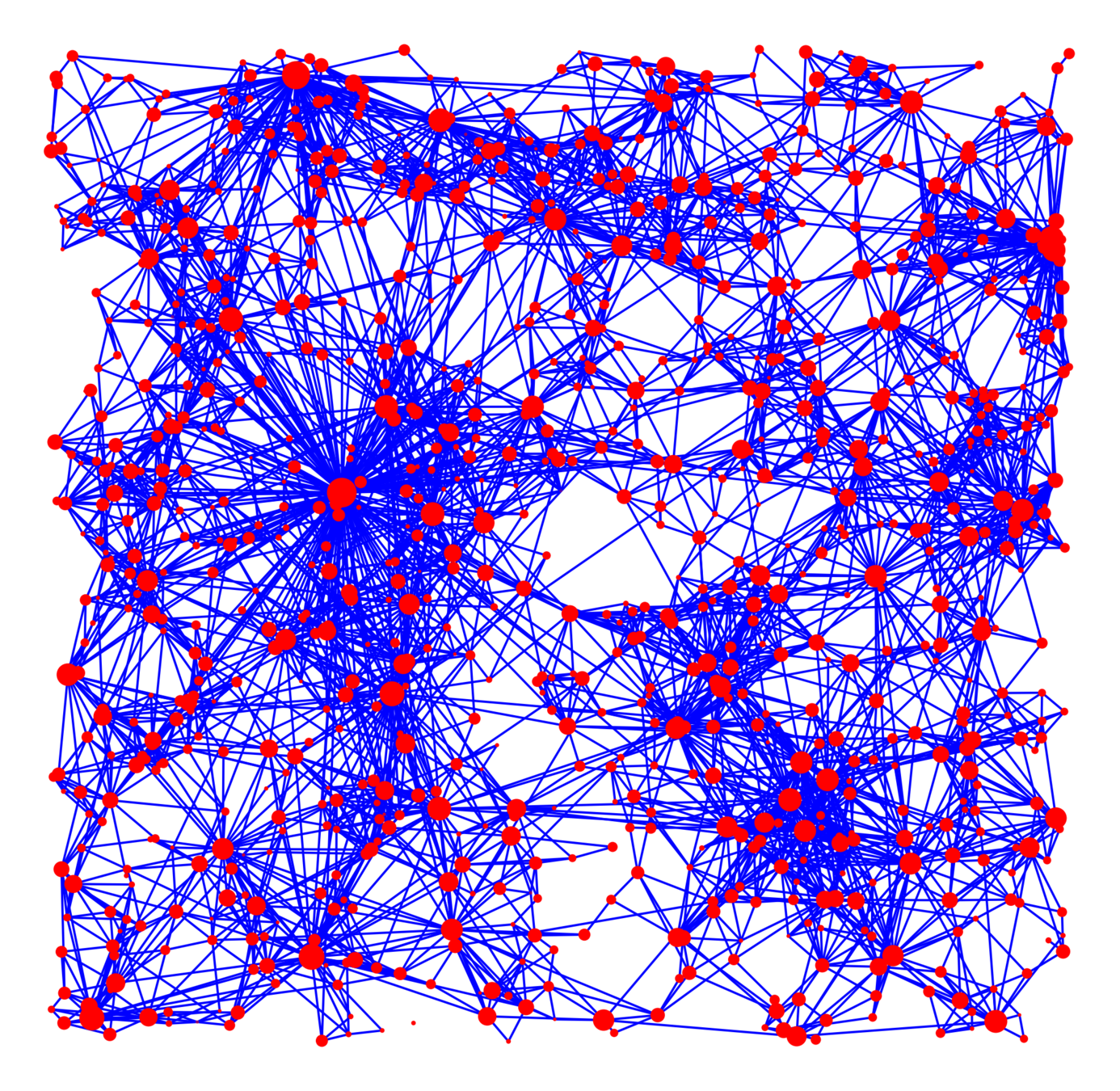
Soft Poisson Boolean model

Edge set $\mathcal{E}_\infty$

$\{u\leftrightarrow v \}\Longleftrightarrow \{w_u^{1/d}+w_v^{1/d}\ge \|x_u-x_v\|\}$
Long-range parameter $\alpha>1$,
Percolation $p\in(0,1]$

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p\bigg(}\frac{ w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\phantom{\bigg)^{\alpha d}}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{ w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Vertex set $\mathcal{V}_\infty$

Locations: Poisson point process intensity $\beta>0$
Power-law i.i.d. weights $\tau>2$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$, $w\ge 1$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

$$(\mathrm{deg}(v) \mid w_v=w) \, = \, \mathrm{Poi}(c_{\alpha, d, \tau}p\beta \cdot w)$$

Soft Poisson Boolean model

Supercriticality assumption

$\theta=\theta_{d, \tau, \alpha, p}(\beta):=\mathbb{P}_{d, \tau, \alpha, p, \beta}^0(0\leftrightarrow \infty)$
$\beta>\beta_c(\alpha, \tau, d, p)=\inf\{\beta: \theta(\beta)>0\}$

Edge set $\mathcal{E}_\infty$

$\{u\leftrightarrow v \}\Longleftrightarrow \{w_u^{1/d}+w_v^{1/d}\ge \|x_u-x_v\|\}$
Long-range parameter $\alpha>1$,
Percolation $p\in(0,1]$

Vertex set $\mathcal{V}_\infty$

Locations: Poisson point process intensity $\beta>0$
Power-law i.i.d. weights $\tau>2$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$, $w\ge 1$

Soft Poisson Boolean model

Questions:

Fixed parameters:

Point process on $\mathbb{R}^d$ intensity $\beta>0$
Power-law exponent $\tau>2$
Long-range parameter $\alpha>1$
Percolation $p\in(0,1]$

[Gracar, Lüchtrath, Mönch '21]

When is $\beta_c<\infty$?
- $d\ge 2$,
Size of the largest connected component $|\mathcal{C}_n^{(1)}|$
- Law of large numbers ($|\mathcal{C}_n^{(1)}|/n\to \theta$)?
- surface-tension behav. in $\mathbb{P}(|\mathcal{C}_n^{(1)}|/n<\theta-\varepsilon)$?
- exponential decay of $\mathbb{P}(|\mathcal{C}_n^{(1)}|/n>\theta+\varepsilon)$?

or $d=1$, and $\alpha\in(1, 2\vee\alpha_\tau)$

Power-law weights

Constant weights

Lower tail*:

If $\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee(1-\frac{\alpha-1}\alpha(\tau-1))}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

\sim^\ast n^{-I(\theta+\varepsilon)}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

*at continuity points of $I(\theta+\varepsilon)$

\ggg

\lll

\sim \exp(-n)

Biskup ['04]

\mathbb{P}(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \varepsilon)

\lesssim\exp\big(-n^{2-\alpha-o(1)}\big)

Lower tail: a too small largest component

|{\color{blue}\text{largest}}|/n \overset{\mathbb{P}}\longrightarrow \theta:=\mathbb{P}^0\big(0\leftrightarrow\infty\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n<\vartheta- \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

Goal 1:

\mathbb{P}^0(|\mathcal{C}_n(0)|>k, 0\notin\mathcal{C}_n^{(1)})

\overset{k\to\infty}\longrightarrow 0

+ local convergence (Giant is almost local)

[vdHofstad, vdHoorn, Maitra '21, vd Hofstad '21]

Goal 2: Prove the theorem

Bootstrapping: Goal 1 proved via method Goal 2

Edge set $\mathcal{E}_\infty$

Long-range parameter $\alpha>1$,
Percolation $p\in(0,1]$

Connection probability

Vertex set $\mathcal{V}_\infty$

Locations: Poisson point process intensity $\beta>0$
Power-law i.i.d. weights $\tau>2$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$, $w\ge 1$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n<\vartheta- \varepsilon \big)\lesssim \exp\big(-n^\zeta\big)

Goal 2 Prove

|{\color{blue}\text{largest}}|/n \overset{\mathbb{P}}\longrightarrow \theta

\Longrightarrow

Power-law weights

Constant weights

Lower tail*:

If $\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee(1-\frac{\alpha-1}\alpha(\tau-1))}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

\sim^\ast n^{-I(\theta+\varepsilon)}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

*at continuity points of $I(\theta+\varepsilon)$

\ggg

\lll

\sim \exp(-n)

Upper tail: polynomial decay when $\tau<\infty$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)=

Related work:

Sum of iid Par($\tau)$: principle of single jump.
Large deviations # edges $E_n$ (vdHvdHKMM '24)
$\mathbb{P}(E_n>\mathbb{E}[E_n] +n\nu)=^\ast (1+o(1))c_\nu n^{-(\tau-2)\lceil\nu\rceil}$.
Inhomogeneous random graphs (J., Zwart '24+)
$\mathbb{P}\big(|\mathcal{C}_n^{(1)}|/n>\rho\big)=^\ast (1+o(1))C_\rho n^{-(\tau-2)\lceil \widetilde h(\rho)\rceil}.$

\Theta(n^{-(\tau-2)\lceil h(\rho)\rceil})

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+w_v^{1/d}}{\|x_u-x_v\|^d}\wedge 1\bigg)^{d\alpha}$$

Challenge: Capture dependency on percolation $p$

Geom. inhom. RG

Long-range percolation

Lower tail*:

If $\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee\frac{3-\tau}{2-(\tau-1)/\alpha}}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical, $\rho\in(\theta, 1)$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

\sim^\ast n^{-I(\rho)}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

*at continuity points of $I(\rho)$

\ggg

\lll

\sim \exp(-n)

Thank you!

Cluster-size decay in supercritical long-range percolation;
With Júlia Komjáthy, Dieter Mitsche;
Electronic Journal of Probability (2024).
Cluster-size decay in supercritical KSRGs;
With Júlia Komjáthy, Dieter Mitsche;
Preprint arXiv: 2303.00712.
Large deviations of the giant in supercritical KSRGs;
With Júlia Komjáthy, Dieter Mitsche;
Preprint arXiv: 2404.02984.

Kernel-based spatial random graphs

Vertex set $\mathcal{V}_\infty$

Spatial locations $x_v\in\mathbb{R}^d$: PPP(1),
i.i.d. weights $w_v\ge 1$: Pareto($\tau$),

Edge set $\mathcal{E}_\infty$

Symmetric kernel $\kappa(w_1, w_2)$,
Edge-density $\beta>0$,
Long-range parameter $\alpha>1$,

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Vertex set $\mathcal{V}_\infty$

Spatial locations $x_v\in\mathbb{R}^d$: PPP(1), or $\mathbb{Z}^d$,
i.i.d. weights $w_v\ge 1$: $\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

Edge set $\mathcal{E}_\infty$

Symmetric kernel $\kappa(w_1, w_2)$,
Edge-density $\beta>0$,
Long-range parameter $\alpha>1$,

\kappa_\mathrm{prod}=w_uw_v

\alpha\in(1,\infty], d\ge 1

Geom. Inhom. RG

\kappa_\mathrm{prod}=w_uw_v

\alpha=\infty, d= 1

Hyperbolic RG

Geom. RG

\kappa_\mathrm{triv}\equiv 1

\alpha=\infty, d \ge 2

Long-range perc.

\kappa_\mathrm{triv}\equiv 1

\alpha\in(1,\infty), d\ge 1

\kappa_{\max}=w_u\vee w_v

Scale-free Gilbert RG

\kappa_{\mathrm{pa}}=(w_u\vee w_v)

\cdot(w_u\wedge w_v)^{\tau-2}

Age-dependent RCM

Theorem. When $\tau<2$ or $\alpha<1$:

Infinite degrees
Bounded diameter

[Deijfen, v.d. Hofstad, Hooghiemstra '13], [Gracar, Grauer, Lüchtrath, Mörters '18]

[Heydenreich, Hulshof, J. '17], [Hirsch '17], [v.d. Hofstad, v.d. Hoorn, Maitra '22],

[J., Komjáthy, Mitsche, '23], [Lüchtrath '22]

Theorem. When $\tau>2$ and $\alpha>1$:

$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau-1)}.$$

$\tau$ small: many hubs

$\alpha$ small: many long edges

The interpolating kernel

Connection probability

$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$

A parameterized kernel: $\sigma\ge 0$

$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$

$\tau: \mathbb{P}(w_v\ge w)=w^{-(\tau-1)}.$
$\sigma$: assortativity
$\sigma$: interpolation

\frac{\sigma}{\tau-1}

\frac1{\tau-1}

\sigma=\tau-1

\tau=2

\sigma=1

\sigma=\tau-2

\sigma=0

SFP/GIRG

Hyperbolic RG

Age-dep. RCM

Scale-free Gilbert

Long-range percolation

Random geom. graph

Nearest-neighbor percolation

Remarks.

$\zeta_\ast<0$: subcritical*
$d\ge 2$:
- $(d-1)/d$
- partial results: upper bounds
Product kernel: 2nd term

No known results

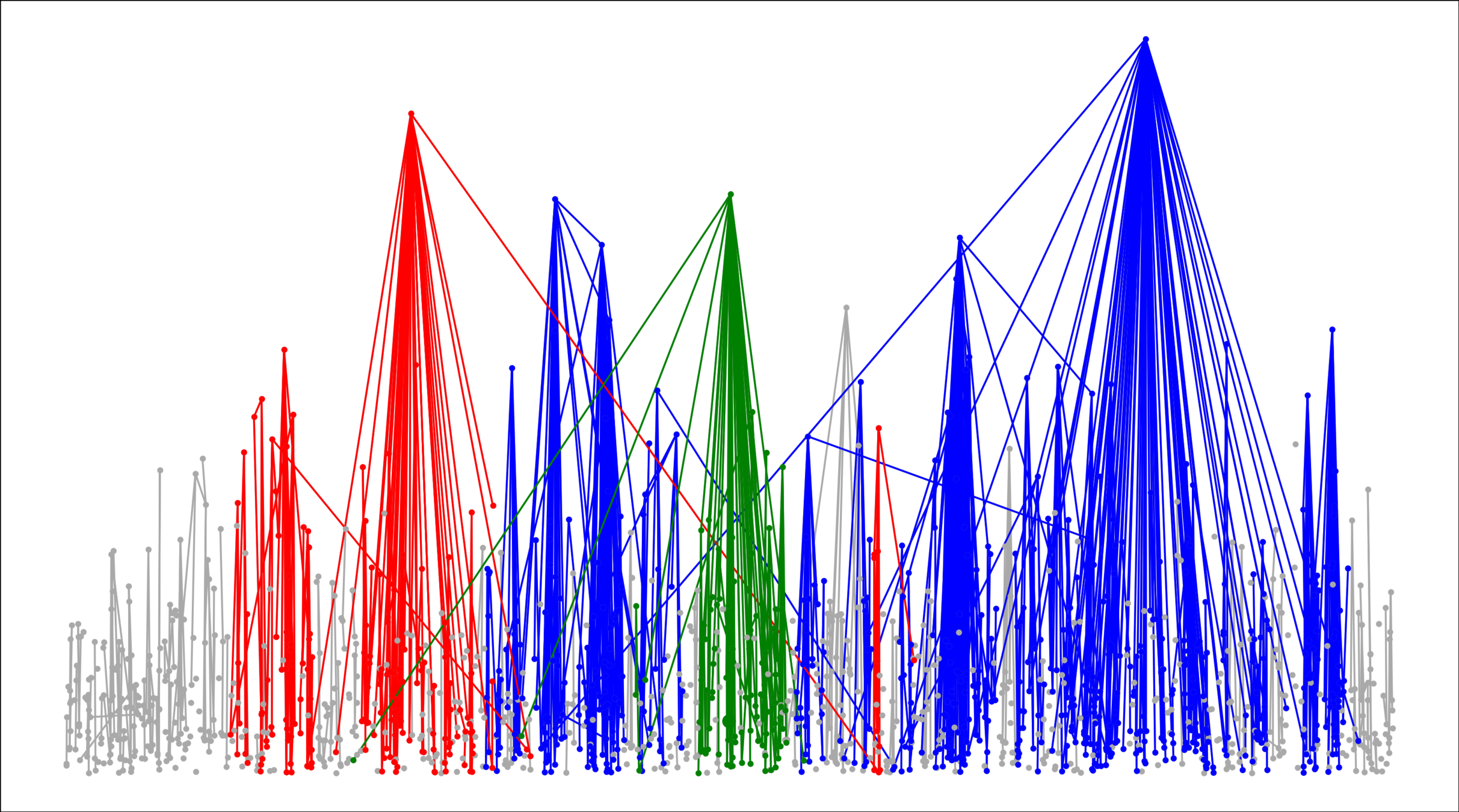
$|{\color{blue}\text{largest}}|/n$
${\color{red}2^{\mathrm{nd}}\text{-largest}}$

Example 1:

Scale-free Gilbert RG in $d=1$

Power-law degrees: $\tau>2$

$d\ge 2$

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\tau)/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

* [Gracar, Lüchtrath, Mönch '22]

Theorem. (J., Komjáthy, Mitsche '23+)

Set

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!2)\!-\!(\tau\!-\!1)/\alpha \}. \end{aligned}

If $\zeta_\ast>0$, then LLN for $|{\color{blue}\text{largest}}|$, and

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\text{largest}}|\big]}\big)

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta_\ast}

Long-range parameter: $\alpha>1$

$\kappa_\mathrm{max}=w_u\vee w_v$

$\kappa_\mathrm{prod}=w_uw_v$

Example 2:

Geom. Inhomog. RG in $d=1$

Lower bounds: cluster-size decay

Aim: Find minimal $\zeta$ s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);

\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)

\sim\mathbb{P}\big(\mathcal{Q}_k\text{ isolated}\big)

\sim \exp\big(-k^\zeta\big)

|\mathcal{C}(0)|\ge k

\Bigg\}

\Theta(k)

\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find $\gamma$ s.t.

\sim k^\zeta

Lower bounds: cluster-size decay

Aim: Find minimal $\zeta$ s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);

|\mathcal{C}(0)|\ge k

\Bigg\}

\Theta(k)

k^\zeta\sim\mathbb{E}\big[|\{v\in\Lambda_k: v\searrow \Lambda_k^c\}|\big]

\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find $\gamma$ s.t.

\sim k^\zeta

Lower bounds: large deviations

\Bigg\}

\rho n/2

\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le \rho n\big)

\ge\,\mathbb{P}\big(\text{all }\frac{2}{\rho}\mathcal{Q}_{\tfrac{\rho n}2}\text{-boxes isolated, $\le\!\rho n$ vertices}\big)

\ge\,\Big(\mathbb{P}\big(\mathcal{Q}_{\tfrac{\rho n}2}\text{-box isolated, $\le\!\rho n$ vertices}\big)\Big)^{2/\rho}

\gtrsim\,\exp\big(-\tfrac{2}\rho(\tfrac{\rho n}2)^\zeta\big)

(FKG)

\Bigg\}

n^{1-\varepsilon}

\Bigg\}

(\delta' \log n)^{1/\zeta}

\mathbb{E}\big[\# \text{small isolated boxes}\big]

\gtrsim\, n^\varepsilon \exp\Big(-\big(\delta \log n)^{1/\zeta}\big)^\zeta\Big)

=\, n^{\varepsilon-\delta}

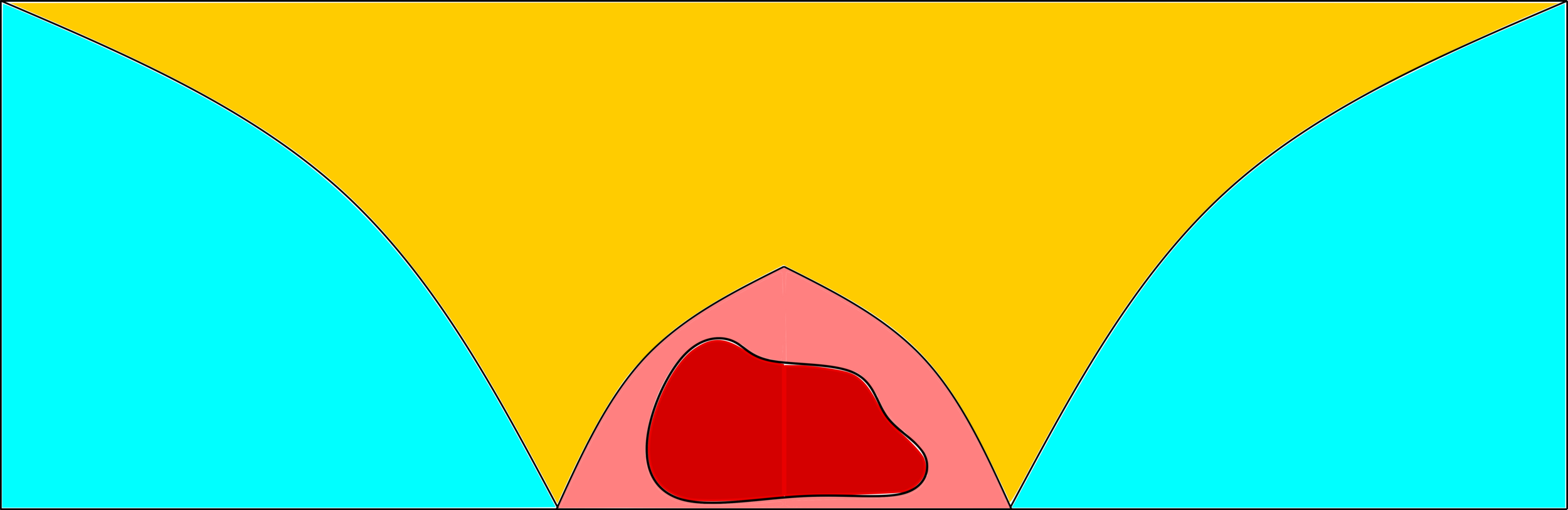
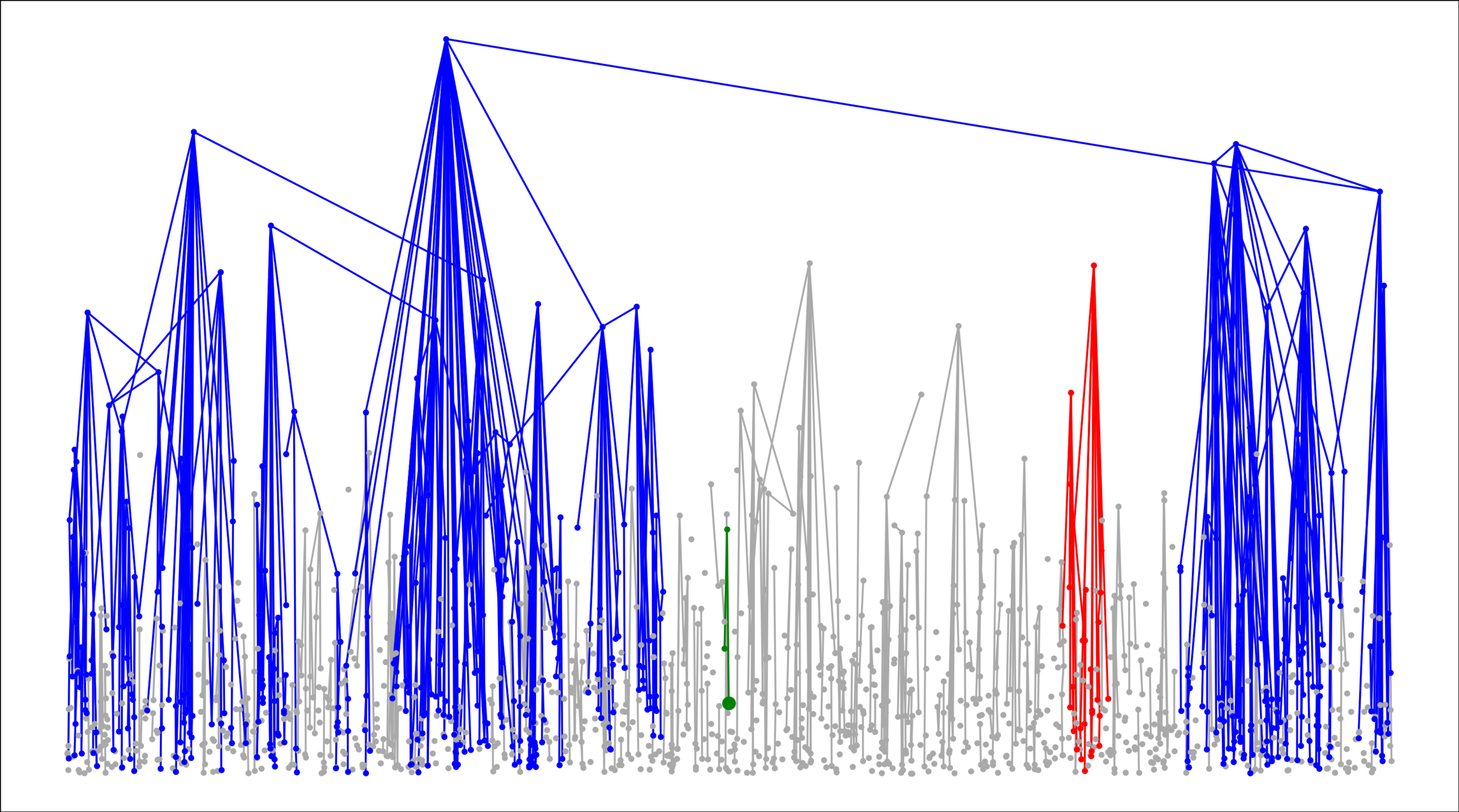
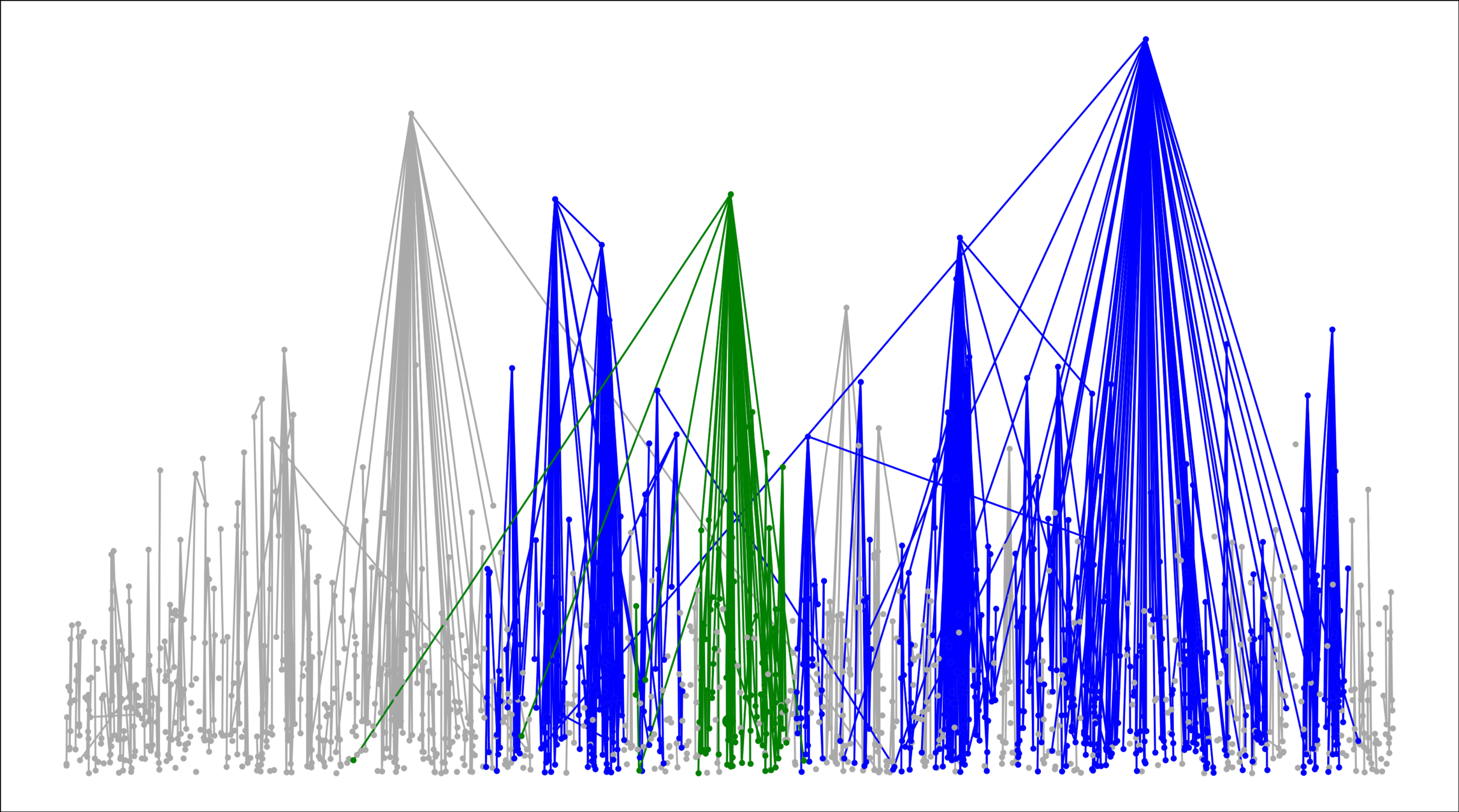
Lower bounds: $|\mathcal{C}_n^{(2)}|$

\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge (\delta \log n)^{1/\zeta}\big)

\ge \, \mathbb{P}\big(\exists \text{isolated small box, no long edges}\big)

\longrightarrow\,\,\,\, \infty

$\delta$ small

Kernel-based spatial random graphs

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

Upper bound: $|\mathcal{C}_n^{(2)}|$

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \exp\big(-n^{2-\alpha}\big)

\mathbb{P}\big(\exists\text{ box without giant}\big)

\mathbb{P}\big(\exists\text{ neighboring giants not conn.}\big)

\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(\nexists\text{ backbone}\big)

\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)

\Bigg\}

\lesssim (n/k)(1-(2k)^{-\alpha})^{(\varepsilon k)^2}

\mathbb{P}\big(\text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)

\lesssim\phantom{(n/k)}\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(\exists \text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)

\lesssim(n/k)\exp\big(-k^{2-\alpha}\big)

Soft Poisson Boolean model

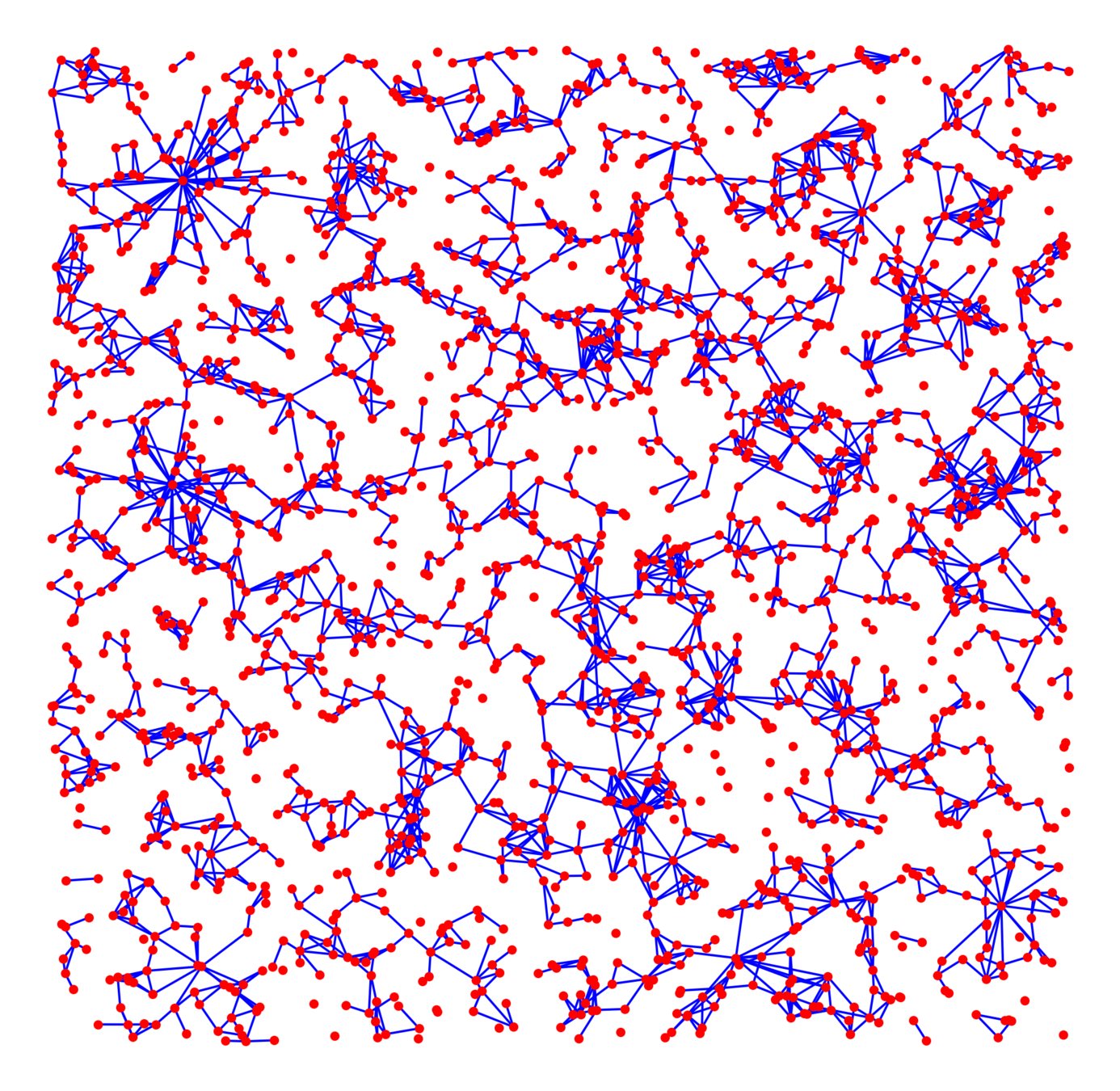
Long-range percolation

Bond percolation on $\mathbb{Z}^d$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

\ggg

Lower tail:

- surface tension

- vertex boundary

Long-range percolation

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)

Edge set $\mathcal{E}_\infty$

Long-range parameter $\alpha>1$,
Edge-density $\beta>0$,
Percolation $p\in(0,1]$

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{\beta}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{\beta}{\|x_u-x_v\|^d}\phantom{\wedge 1}\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p\bigg(}\frac{1}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{1}{\|x_u-x_v\|^d}\phantom{\wedge 1}\bigg)^\alpha$$

Soft Poisson Boolean model

Edge set $\mathcal{E}_\infty$

Long-range parameter $\alpha>1$,
Percolation $p\in(0,1]$

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{ \phantom{w_u^{1/d}+ w_v^{1/d}}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Vertex set $\mathcal{V}_\infty$

Spatial locations: Poisson point process intensity $\beta>0$
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{ {\color{darkred}w_u^{1/d}+w_v^{1/d}}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Kernel-based spatial random graphs

Edge set $\mathcal{E}_\infty$

Long-range parameter $\alpha>1$,
Edge-density $\beta>0$,
Percolation $p\in(0,1]$

Connection probability

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta\cdot (w_u\cdot w_v)}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

Geom. inhom. RG

Long-range percolation

Lower tail*:

If $\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\lesssim\exp\big(-n^{{\color{darkgray}\frac{d-1}d\vee}(2-\alpha)}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)

\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee\frac{3-\tau}{2-(\tau-1)/\alpha}}\big)

\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Remainder: Lower tail LRP - Upper tail GIRG

*log-corrections at phase transition

Upper tail:

If non-critical, $\rho\in(\theta, 1)$

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

\sim^\ast n^{-I(\rho)}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

*at continuity points of $I(\rho)$

\ggg

\lll

\sim \exp(-n)

{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\text{Law of large numbers}

{\text{\color{blue}Lower tail large deviations}}

Challenge: Delocalized components

\binom{n}k \sim n^k \gg n\exp\big(k^\zeta\big)

# possibilities for $|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k$

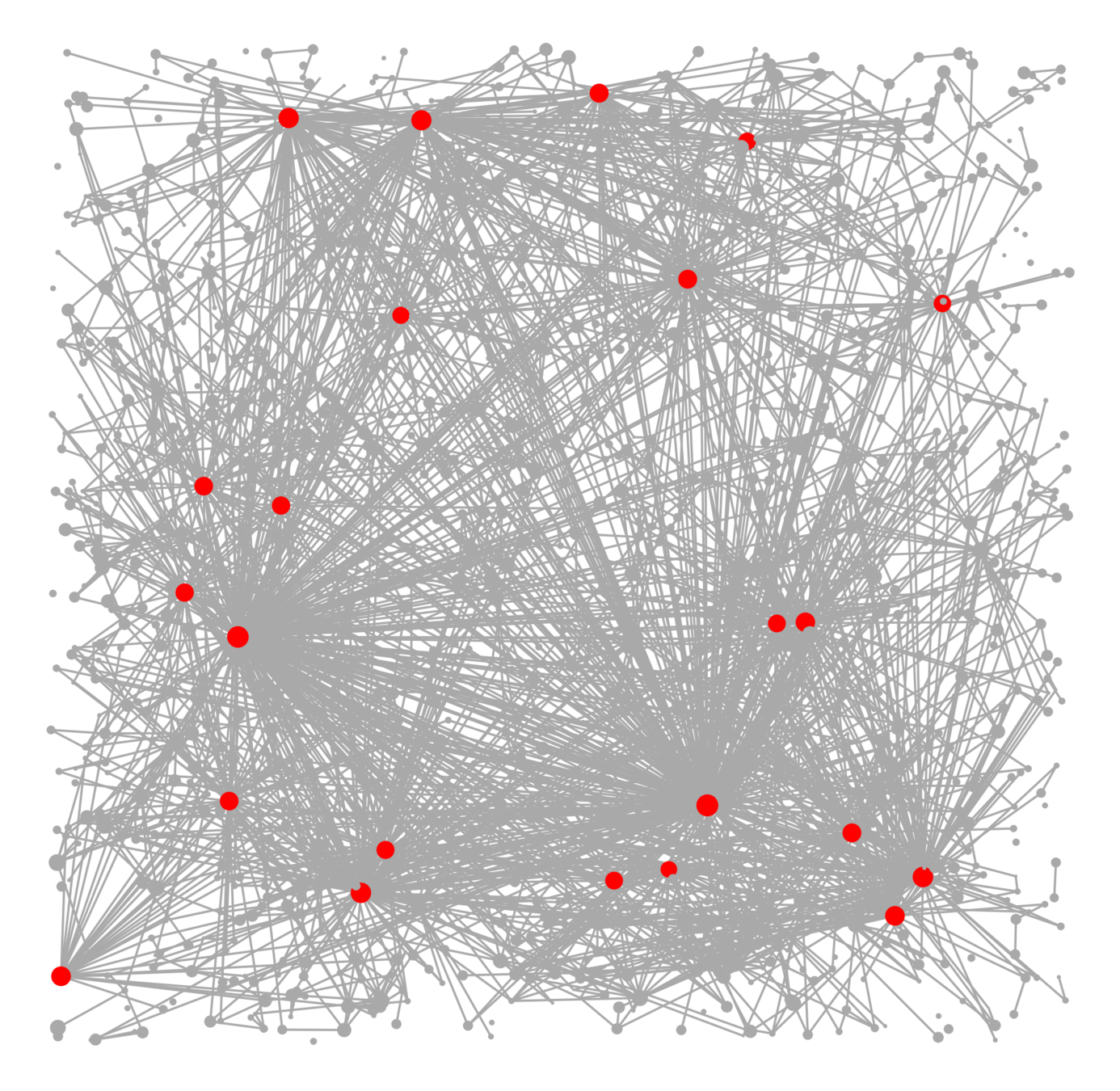
Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Questions

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Questions

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Previous results

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\lesssim(\log n)^{??}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}d/(d-1)}

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\!\big(\!\!-\!k^{\color{darkred}(d-1)/d}\big)

\sim \exp\big(\!-\!n^{\color{darkred} (d-1)/d}\big)

\lesssim \exp\big(\!-\!n^{\max(2-\alpha-o(1), (d-1)/d)}\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon)\mathbb{E}[|{\color{blue}\mathrm{largest}}|]\big)

[Alexander & Chayes & Chayes '90], [Grimmett & Marstrand, '90], [Kesten & Zhang '90], ..., [Deuschel, Pisztora, '96], [Biskup '04], [Penrose '05], [Sly & Crawford'12], [Kiwi & Mitsche '17], [Lichev, Lodewijks, Mitsche, Schapira '22], [Bläsius, Friedrich, Ruff, Zeiff, '23]

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}2/(3-\tau)}

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)

\lesssim \exp\big(\!-\!n^{\color{darkred}(3-\tau)/2}\big)

Conjecture: $\exists \zeta\in \big[\tfrac{d-1}{d},1\big)$:

\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\mathrm{largest}}|\big]}\big)

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta}

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}| \lesssim (\log n)^{1/\zeta}

{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

|{\color{blue}\text{largest}}| \text{ linear}

{\color{blue}\text{Lower tail large deviations}}

{\color{blue}\text{Lower tail of large deviations}}

{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\text{Law of large numbers}

{\text{\color{blue}Lower tail large deviations}}

What about other value $\zeta_\ast$?

\zeta_\ast := \max\{2\!-\!\alpha, (3\!-\!\tau)\big/(2\!-\!(\tau\!-\!1)/\alpha) \}

Description of weight distribution in large components

Prevent "small-to-large" merging

Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Answered questions ($d=1$)

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

(Second-)largest component in supercritical spatial random graphs

Cluster-size decay

Second-largest component

Open problems:

Largest component:
- Linear in box size
- Law of large numbers
- Large deviations

Answered questions ($d=1$)

Phase transition boundaries.
Partial results $d\ge 2$
Extension from PPP to grid
Central limit theorem

$\zeta\in\big[(d-1)/d, 1\big)$

{\color{green}\text{Cluster-size decay}}

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}

|{\color{red}\mathcal{C}_n^{(2)}}| \lesssim (\log n)^{1/\zeta}

{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

|{\color{blue}\mathcal{C}_n^{(1)}}| \text{ linear}

{\color{blue}\text{Lower tail large deviations}}

{\color{blue}\text{Lower tail of large deviations}}

\alpha

\tau

Small

Large

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}| \lesssim (\log n)^{1/\zeta}

{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

|{\color{blue}\text{largest}}| \text{ linear}

{\color{blue}\text{Lower tail large deviations}}

{\color{blue}\text{Lower tail of large deviations}}

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} + \varepsilon\big]\big)\gtrsim \exp\big(-n^\zeta\big)

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} - \varepsilon\big)\gtrsim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le 2\varepsilon \big)\longrightarrow 0

Remarks.

$\zeta_\ast<0$: subcritical*
$d\ge 2$:
- $(d-1)/d$
- partial results: upper bounds
Product kernel: 2nd term

Power-law degrees: $\tau>2$

$d\ge 2$

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\tau)/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

* [Gracar, Lüchtrath, Mönch '22]

Theorem. (J., Komjáthy, Mitsche '23+)

Set

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!2)\!-\!(\tau\!-\!1)/\alpha \}. \end{aligned}

If $\zeta_\ast>0$, then LLN for $|{\color{blue}\text{largest}}|$, and

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\text{largest}}|\big]}\big)

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta_\ast}

Long-range parameter: $\alpha>1$

Example 2:

Geom. Inhomog. RG in $d=1$

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Scale-free Gilbert RG

Random geom. graph

Nearest-neighbor percolation

Large deviations of the giant in spatial random graphs

Supercritical bond percolation on \(\mathbb{Z}^d\)

Soft Poisson Boolean model

Soft Poisson Boolean model

Soft Poisson Boolean model

Main result: large deviations for the giant component

Lower tail: a too small largest component

Goal 2 Prove

Main result: large deviations for the giant component

Upper tail: polynomial decay when \(\tau<\infty\)

Main result: large deviations for the giant component

Thank you!

Kernel-based spatial random graphs

The interpolating kernel

Lower bounds: cluster-size decay

Lower bounds: cluster-size decay

Lower bounds: large deviations

Lower bounds: \(|\mathcal{C}_n^{(2)}|\)

Kernel-based spatial random graphs

Upper bound: \(|\mathcal{C}_n^{(2)}|\)

Long-range percolation

Soft Poisson Boolean model

Kernel-based spatial random graphs

Remainder: Lower tail LRP - Upper tail GIRG

Upper bounds

Challenge: Delocalized components

Components in supercritical graphs

Components in supercritical graphs

Previous results

Conjecture: \(\exists \zeta\in \big[\tfrac{d-1}{d},1\big)\):

Lower bounds

Upper bounds

Upper bounds

What about other value \(\zeta_\ast\)?

Components in supercritical graphs

(Second-)largest component in supercritical spatial random graphs

Lower bounds

Upper bounds

Lower bounds

Upper bounds

Lower bounds

Upper bounds

Lower bounds

Upper bounds