Distances and component sizes
in scale-free random graphs
Joost Jorritsma, PhD








Florence Nightingale Bicentennial Fellowship
Research talk



Erdős–Rényi Random Graph

Nearest-Neighbour Percolation on \(\mathbb{Z}^d\)
Random Graphs: Probability, Combinatorics, Physics, Epidemiology
Motivation
- Real-world networks:
hubs and long edges - New phenomena
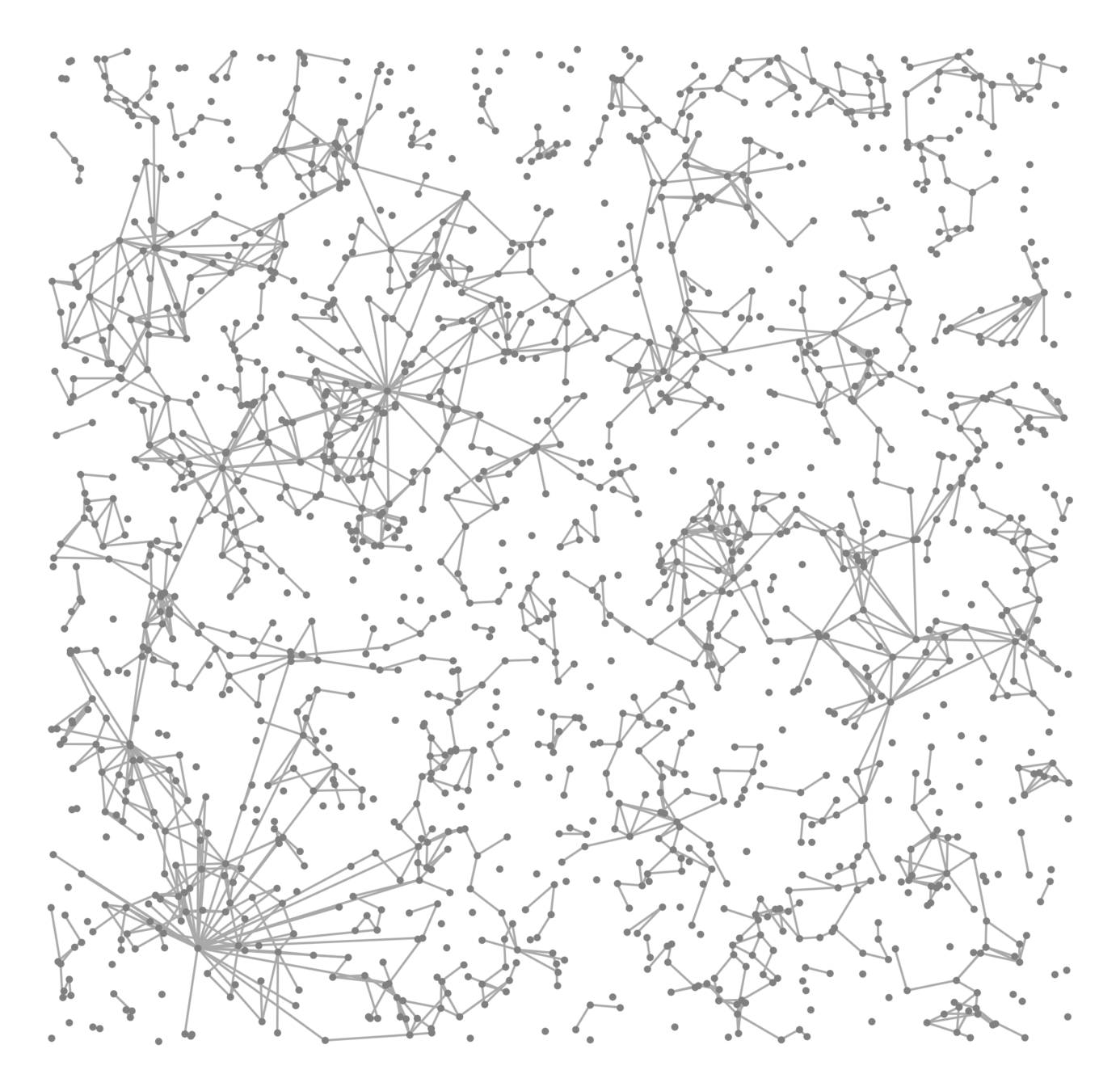

Inhomogeneous Percolation
Preferential attachment





3x Information diffusion in random graphs


Distances


Component sizes
Intervention strategies


FINAL SIZE
Internet: a growing network of routers and servers
~1969: 2 connected sites
Time
~1989: 0.5 million users
~2023: billions of devices
- [Faloutsos, Faloutsos & Faloutsos, '99]:
-
Short average distance:
Quick spread of information
-
Short average distance:

~1999: 248 million users
Distance evolution in a growing network
1999
\(\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4\)
2005
\(\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3\)
2023
\(\mathrm{dist}_{{\color{red}'23}}(u_{'99}, v_{'99}) = 2\)
21 possible networks
Attachment rule:
Favour connecting to high-degree vertices, \(\tau\): tail of power-law degree distribution
2005
\(\phantom{\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3}\)
Distance evolution
Distance evolution: hydrodynamic limit
Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then
$$ \mathbb{P}\bigg(\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|>\varepsilon\bigg)\longrightarrow 0.$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then
$$ \phantom{\mathbb{P}\bigg(}\phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{>\varepsilon\bigg)\phantom{\longrightarrow} 0.}$$
Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(\phantom{t'=T_t(a):=t\exp\big(\log^a(t)\big)}\) for \(\phantom{a\in[0,1]}\), then
$$ \phantom{\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.}$$
Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then
$$ \phantom{\mathbb{P}\bigg(}\phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - \phantom{(1-a)\frac{4}{|\log(\tau-2)|}}\right|\phantom{>\varepsilon\bigg)\longrightarrow 0.}$$
-
Dynamics in PAMs.
-
Generalization with edge weights: random transmission times





Novelties
-
Fast spreading among influentials;
Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then
$$ \mathbb{P}\bigg(\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|>\varepsilon\bigg)\phantom{\longrightarrow 0.}$$
Information spreading on random graphs


Distances


Component sizes
Intervention strategies


FINAL SIZE

Intervention strategies


Real networks contain many triangles!
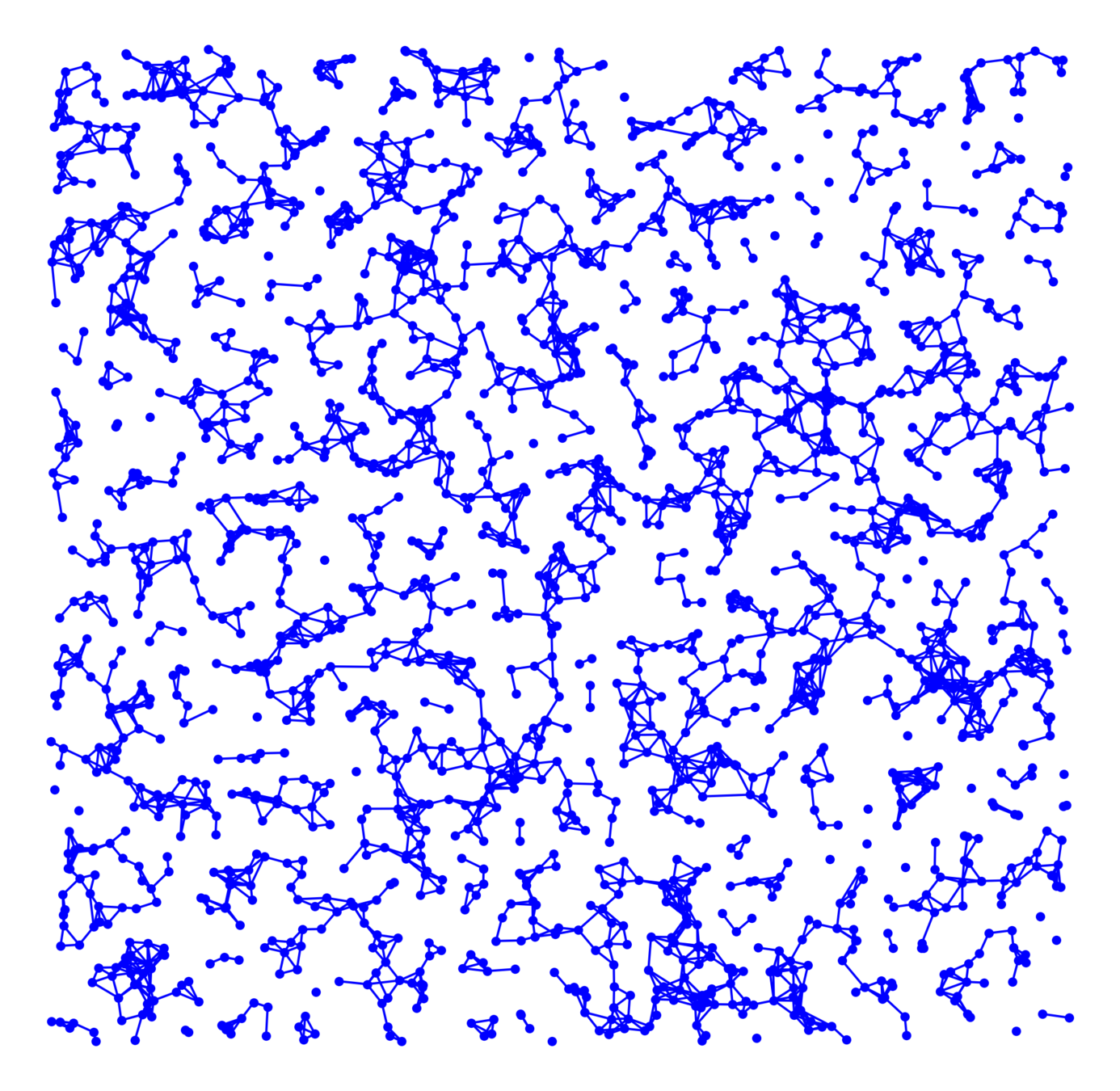
Do real networks look like this?

Large deviations (rare events) of cluster sizes:
- Much larger/smaller (final) size of epidemic than expected.
What is the influence of long edges and high-degree vertices?





Hyperbolic random graph
Scale-free percolation
Long-range percolation
Soft Poisson-Boolean model
Random geom. graph
Nearest-neighbour percolation

Kernel-based spatial random graphs
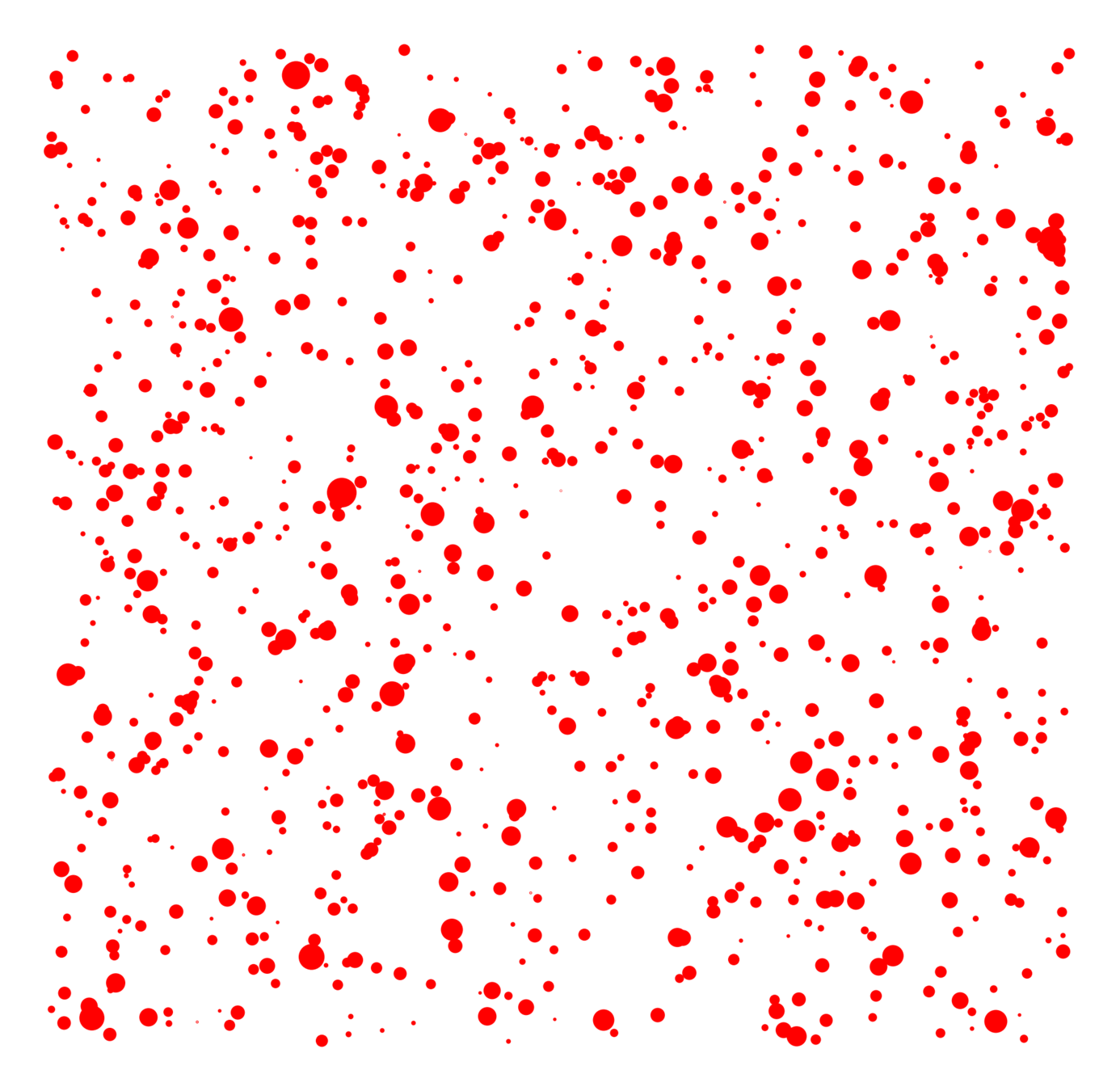

Only four parameters
Vertex set
- Spatial locations, \(\mathbb{Z}^d\) or Poisson point process
- Vertex weights
(iid Pareto or constant)
Edge more likely if
- Spatially nearby,
- High weight
Clusters in supercritical graphs
-
Largest component \({\color{blue}\mathcal{C}_n^{(1)}}\):
- Linear in box size: giant component
- Law of large numbers
- Much smaller giant
- Much larger giant
Questions

Theorem [J., Komjáthy, Mitsche, '23+]
We find explicit \(\zeta\in[1/2,1)\), \(\theta\in(0,1)\) s.t.
- Lower tail: small final size
If enough long edges or no hubs













Novelties
-
Reversed discrepancy: slower upper tail.
-
Long edges can beat surface tension: any ;
-
First (upper) LDP for giant in spatial graph;
-
drives also other cluster-size distributions
What is the influence of long edges and high-degree vertices?
- Upper tail: large final size
If hubs are present, we find rate funtion \(I(\varepsilon)\):
What is the influence of long edges and high-degree vertices?
Information spreading on random graphs


Distances


Component sizes
Intervention strategies


FINAL SIZE

Distances and component sizes
in scale-free random graphs
Joost Jorritsma, PhD








Florence Nightingale Bicentennial Fellowship
Research talk


Surface tension in supercritical nearest-neighbour percolation

[Grimmett & Marstrand '90, Kesten & Zhang '90, Pisztora '96]
[Lebowitz & Schonmann '88]
- Discrepancy: faster upper tail
- No precise asymptotics
What is the influence of long edges and high-degree vertices?
Lower tail: small final size
Upper tail: large final size
Kernel-based spatial random graphs
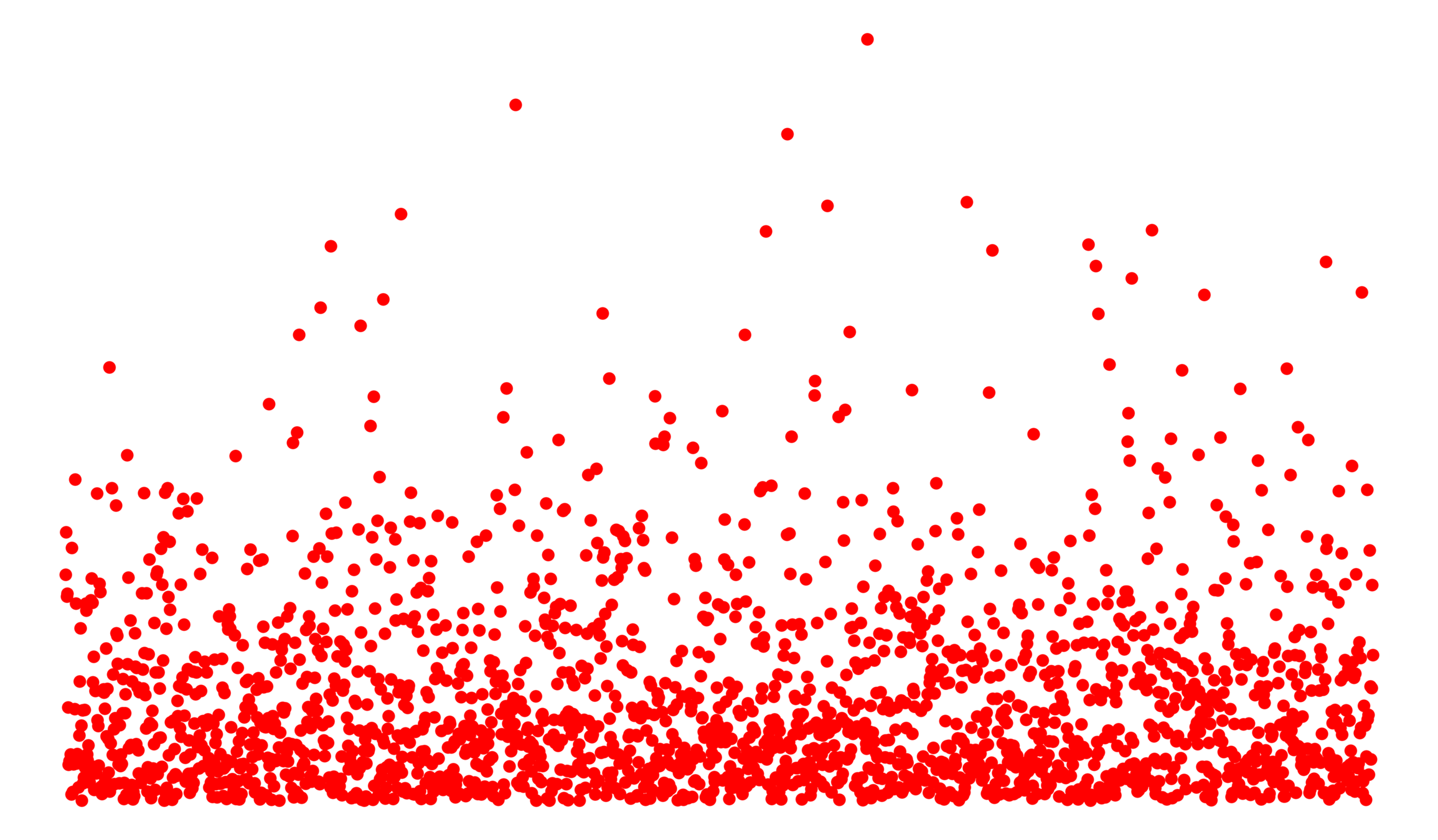
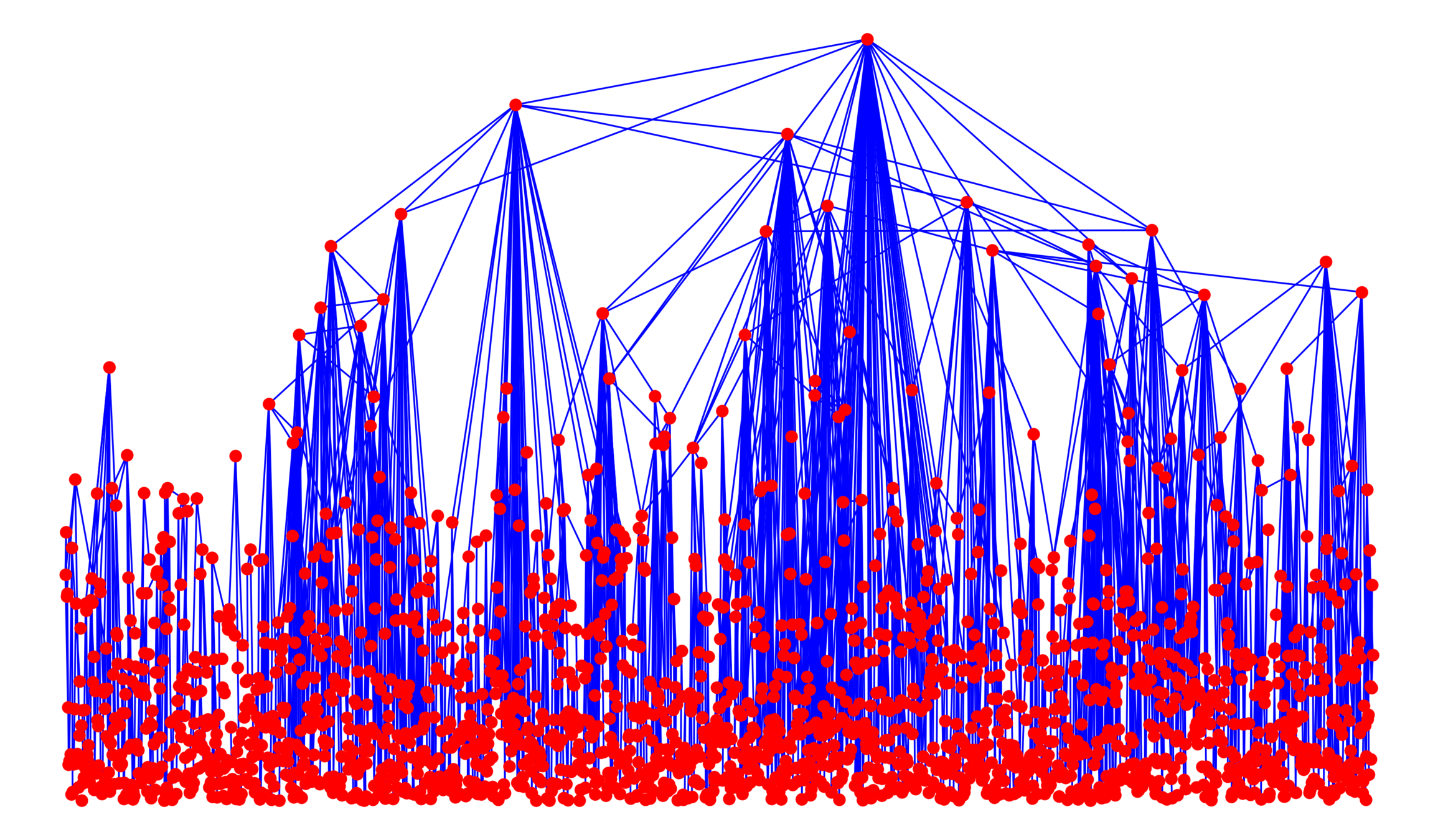
Edge set \(\mathcal{E}_\infty\)
- Symmetric kernel \(\kappa(w_u, w_v)\),
- Long-range parameter \(\alpha\in(1,\infty]\),
- Edge-density \(\beta>0\),
Connection probability
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$
Vertex set \(\mathcal{V}_\infty\)
-
Spatial locations, either
- Lattice \(\mathbb{Z}^d\)
- Poisson point process (unit intensity)
- Power-law i.i.d. weights \(w_v\ge 1\):
\(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\phantom{\|x_u-x_v\|^d}}\phantom{\bigg)^\alpha\wedge 1}$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\phantom{\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\phantom{\wedge 1}$$
Components in supercritical graphs
-
Largest component \({\color{blue}\mathcal{C}_n^{(1)}}\):
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations
Questions






Lower bounds: cluster-size decay
Aim: Find minimal \(\zeta\) s.t.




Aim: Find \(\gamma\) s.t.
Upper bounds
Challenge: Delocalized components
# possibilities for \(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\)