Distances and component sizes

in scale-free random graphs

Joost Jorritsma

PhD Defense

Information spreading in networks

Mathematical models for information spreading

Problem: 
Unknown network dynamics involved
Solution: 
Random graph
Goals: 
Understand networks 

+ spreading model
Problem: 
Unknown network dynamics involved
Solution: 
Random graph
Goals: 
Understand networks Fascinating math

+ spreading model

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

Information spread: three related parts

Distances

Component sizes

Intervention strategies

MODELS
RESULTS
Fascinating,
because...
FINAL SIZE

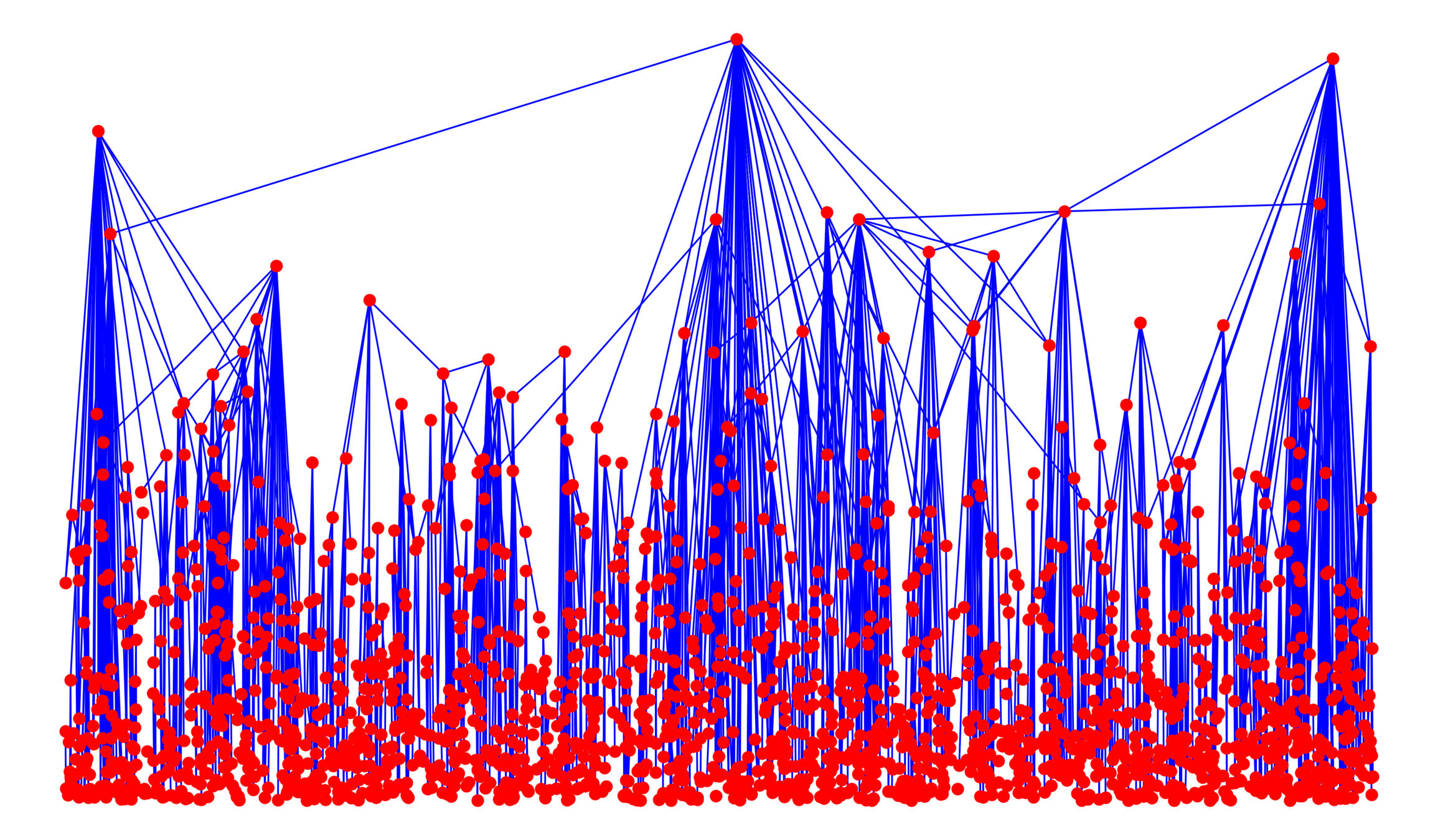
Internet: a growing network of routers and servers

~1969: 2 connected sites

Time

~1989: 0.5 million users

~2023: billions of devices

  • [Faloutsos, Faloutsos & Faloutsos, '99]:
    • Short average distance:
      Quick spread of information

~1999: 248 million users

Distance evolution in a growing network

1999

\(\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4\)

2005

\(\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3\)

2023

\(\mathrm{dist}_{{\color{red}'23}}(u_{'99}, v_{'99}) = 2\)

21 possible networks

Attachment rule:

Favour connecting to high-degree vertices

2005

\(\phantom{\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3}\)

Distance evolution

Distance evolution: hydrodynamic limit

Theorem [J., Komjáthy '22]. Assume \(c_\tau<0\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \mathbb{P}\bigg(\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|>0.001\bigg)\longrightarrow 0.$$

Theorem [J., Komjáthy '22]. Assume \(c_\tau<0\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \phantom{\mathbb{P}\bigg(}\phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{>0.001\bigg)\phantom{\longrightarrow} 0.}$$

Theorem [J., Komjáthy '22]. Assume \(c_\tau<0\).
Let \(\phantom{t'=T_t(a):=t\exp\big(\log^a(t)\big)}\) for \(\phantom{a\in[0,1]}\), then

$$ \phantom{\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.}$$

Theorem [J., Komjáthy '22]. Assume \(c_\tau<0\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \phantom{\mathbb{P}\bigg(}\phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - \phantom{(1-a)\frac{4}{|\log(\tau-2)|}}\right|\phantom{>0.001\bigg)\longrightarrow 0.}$$

  • Dynamics in PAMs.
  • Stochastic process becomes deterministic;
  • Fast spreading among influentials;
Fascinating, because

Theorem [J., Komjáthy '22]. Assume \(c_\tau<0\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \mathbb{P}\bigg(\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|>0.001\bigg)\phantom{\longrightarrow 0.}$$

Information spreading on random graphs

Distances

Component sizes

Intervention strategies

MODELS
FINAL SIZE
RESULTS
Fascinating,
because...

Real networks contain many triangles!

FINAL SIZE

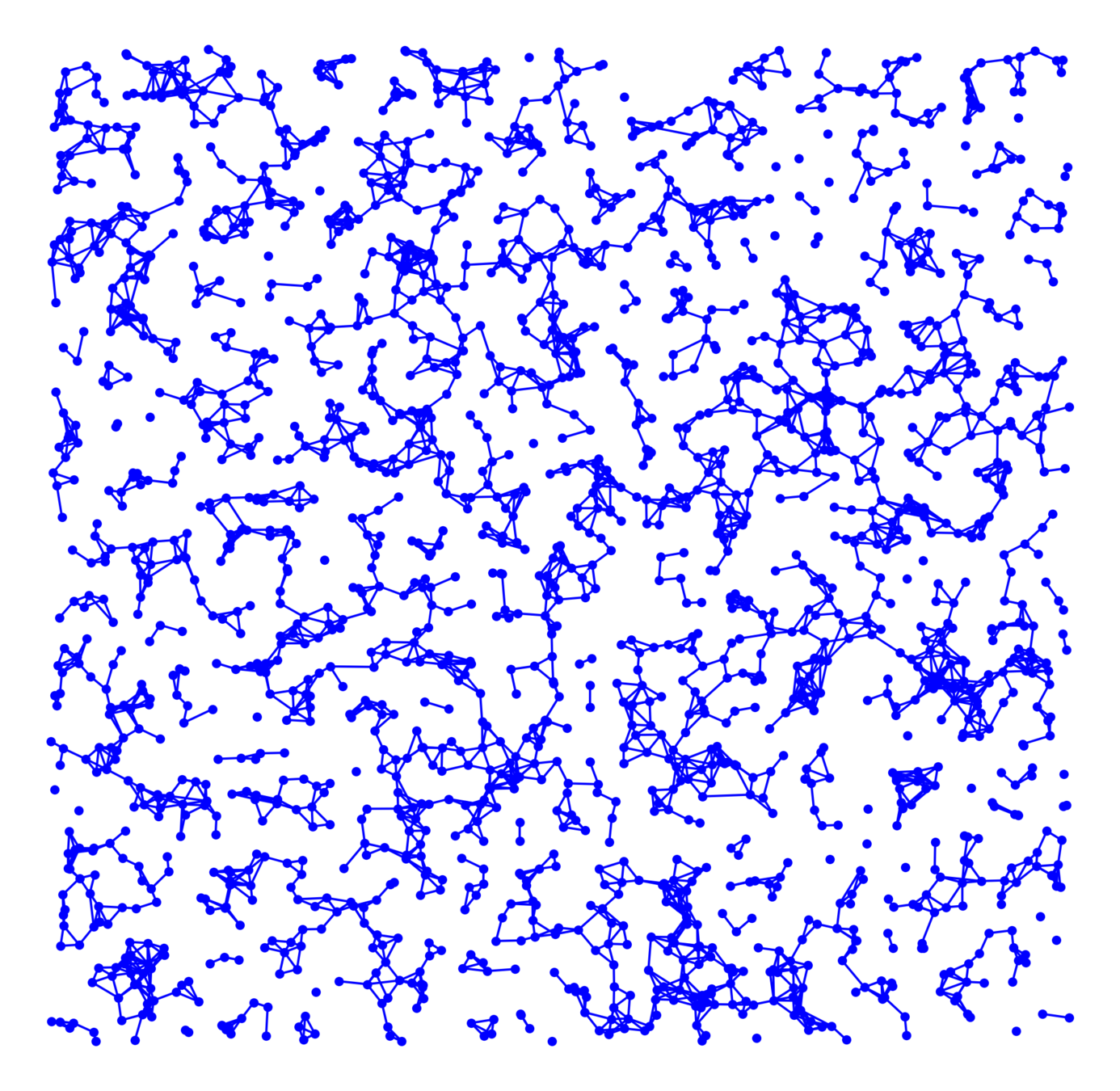
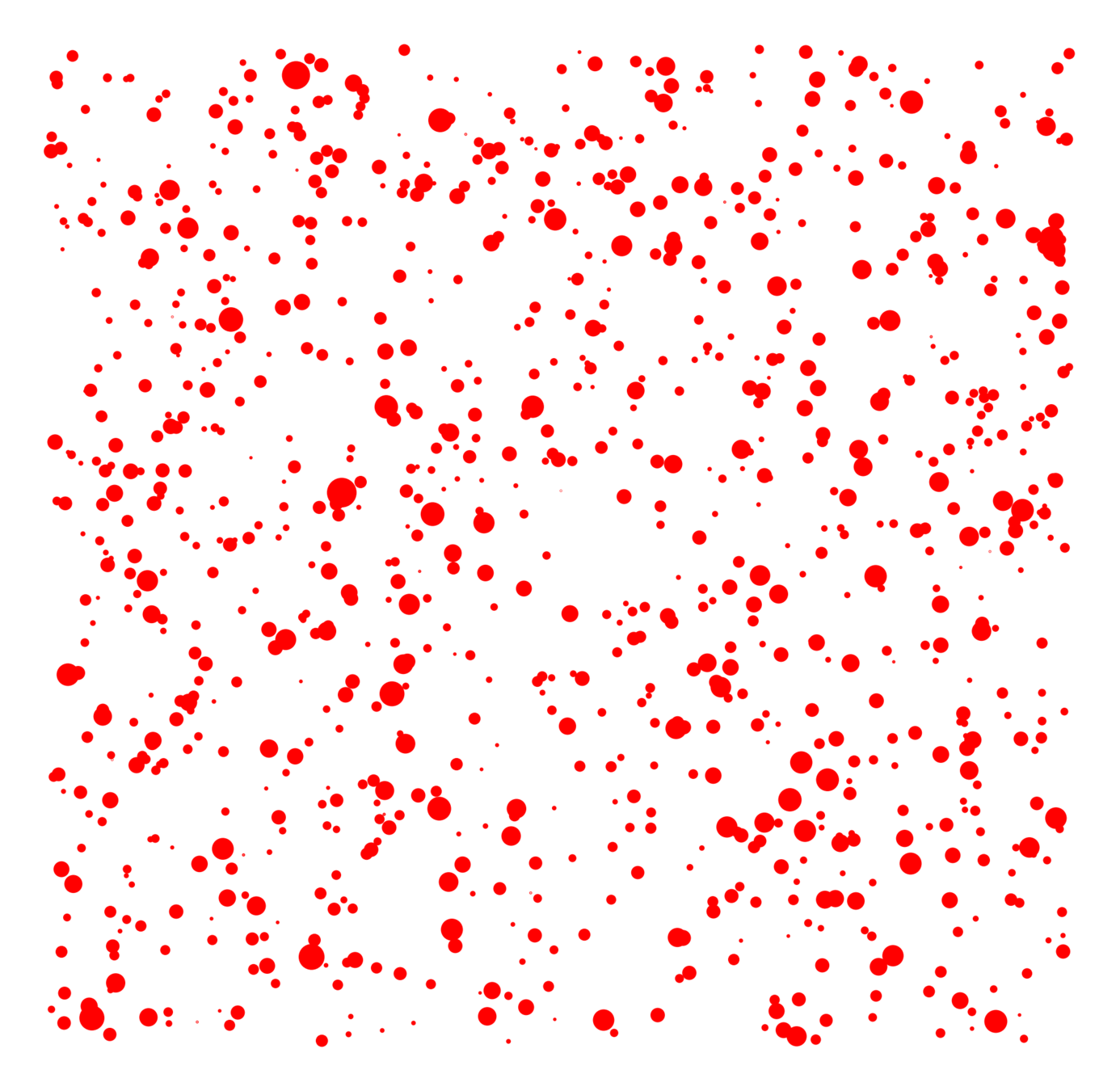
Do real networks look like this?

Kernel-based spatial random graphs

Only four parameters

Vertex set

  • Spatial locations,
  • i.i.d. (power-law) weights

Edge more likely if

  • Spatially nearby,
  • High weight
FINAL SIZE
FINAL SIZE

Connected components in random graphs

FINAL SIZE

Connected components in spatial graphs

  • Largest component \({\color{red}\mathcal{C}_n^{(1)}}\):

     
  • Component of the origin \({\color{green}\mathcal{C}_n(0)}\):

     
  • Second-largest component \({\color{blue}\mathcal{C}_n^{(2)}}\):

Three questions

\mathbb{P}\Big(|{\color{red}\mathcal{C}_n^{(1)}}|\le (1-\varepsilon)\mathbb{E}\big[|{\color{red}\mathcal{C}_n^{(1)}}|\big]\Big)=
\mathbb{P}\Big(0\notin{\color{red}\mathcal{C}_n^{(1)}}\,\big|\, |{\color{green}\mathcal{C}_n(0)}|\ge k\Big)=
|{\color{blue}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{(\log n)^{1/\zeta}}\big)
FINAL SIZE

Connected components in spatial graphs

\exp\big(-\Theta(n^\zeta)\big)
\exp\big(-\Theta(k^\zeta)\big)
|{\color{blue}\mathcal{C}_n^{(2)}}|=\Theta\big((\log n)^{1/\zeta}\big)
  • Structural information.
  •    3 related quantities;
  • Not only                      ;
Fascinating, because
(\ge)
FINAL SIZE

Answers: there is \(\zeta\in(0,1)\) s.t.

\zeta\!\in\!(0,1/2]\!\cup\!\big\{\tfrac23, \tfrac34,\tfrac45,..., 1\big\}
  • Largest component \({\color{red}\mathcal{C}_n^{(1)}}\):

     
  • Component of the origin \({\color{green}\mathcal{C}_n(0)}\):

     
  • Second-largest component \({\color{blue}\mathcal{C}_n^{(2)}}\):
\mathbb{P}\Big(|{\color{red}\mathcal{C}_n^{(1)}}|\le (1-\varepsilon)\mathbb{E}\big[|{\color{red}\mathcal{C}_n^{(1)}}|\big]\Big)=
\mathbb{P}\Big(0\notin{\color{red}\mathcal{C}_n^{(1)}}\,\big|\, |{\color{green}\mathcal{C}_n(0)}|\ge k\Big)=
|{\color{blue}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{(\log n)^{1/\zeta}}\big)

Information spreading on random graphs

Distances

Component sizes

Intervention strategies

MODELS
FINAL SIZE
RESULTS
Fascinating,
because...

Distances and component sizes

in scale-free random graphs

Joost Jorritsma

PhD Defense

Distances and component sizes

in scale-free random graphs

and other exciting projects

TOTAL SIZE
[Krioukov et al., '10]: Hyperbolic random graph 
Good model for real networks

Kernel-based spatial random graphs

  • Little known about components.
  • Three sources of randomness;
  • Generalizes previous models;
Fascinating, because

Four parameters to interpolate/switch

Vertex set

  • Spatial locations,
  • i.i.d. (power-law) weights

Edge more likely if

  • Spatially nearby,
  • High weight
TOTAL SIZE
Made with Slides.com