BCS Technical Interview Workshop #2
March 21st, 2020
-
Intro/Warm-up
-
Dynamic ProGRAMMING
-
Exercises
Jordan Chiu
- Pronouns: he/him
- Public Services & Procurement Canada (Apr - Aug 2019)
- CA Technologies (Sep - Nov 2018)
Facilitator

DISCLAIMERS
- This workshop will be recorded and released on YouTube
- This has been designed for people who:
- Are currently in CPSC 210, 221, and/or 310; and
- Have been to or seen Workshop #1
- Don't be discouraged!
- You will encounter terms and/or data structures that are unfamiliar to you
- You may not be able to solve most, or perhaps any, of these questions
- If you've already taken CPSC 320 or are familiar with more advanced algorithms, you may not get a lot out of this session
- But you're welcome to join us regardless!
General Tips
-
Talk! The worst thing you can do is solve a problem in silence
-
Ask questions for clarification
-
DO NOT start coding right away; solve the problem first
-
Talk through your solution out loud
-
Make sure you solve the problem that you're given
-
-
Know that you won't solve everything
-
Don't worry too much about syntax, unless you're told to
-
Choose your favourite language if you can
-
For more challenging algorithms especially, interviewers will care more about your clear logic than your code
-
-
Once you're done, state complexity in big-O notation and be able to justify it
Warm-up problem
A bracket string is called "balanced" if every opening bracket has a matching closing bracket. For example, all these strings are balanced: "[]{}", "{[()]}", "{{[[(())]]}}". These strings are not balanced: "{[(])}", "{[}]".
Write a function that takes in a bracket string and returns "YES" if the string is balanced, and "NO" if it's not. You may assume that the string only contains the characters "(", ")", "{", "}", "[", and "]".
Source: adapted from an interview at Amgen
Dynamic Programming
-
"Simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner"
-
Take a complex problem
-
Break it into smaller sub-problems
-
Solve those sub-problems optimally
-
Use those solutions to solve the more complex problem optimally
-
STRATEGIES
- Start with a brute-force (non-optimal) solution description
- Solve small problems
- Write a recursion (if you need to)
- Argue that your complexity is better than brute-force
- (Implement)
Why DP for this workshop?
-
DP problems are fairly common in more advanced interviews
-
Tests your communication skills more so than regular problems
-
Most of the work for DP comes from talking out a solution
-
Focus on the logic behind it
-
Once you have a solution fully fleshed out, coding it up tends to be trivial (barring minor details)
-
DEMO - Change Problem
You have coins worth $1, $8, and $10. Design an algorithm that, given a number n, minimizes the number of coins you use to get to exactly $n (i.e. return the minimum number of coins).
Note: Taking the next largest possible coin at each step (a.k.a. the "greedy" approach) won't work.
Consider $24. Taking the largest possible coin will result in you getting two $10 coins and four $1 coins (6 coins total). Clearly, this is more than the optimal solution which is three $8 coins (3 coins total).
Questions?
Your turn!
- Get some paper and pens
- Work through the problem out loud by yourself
- You'll get 5-15 minutes for each problem
- There's more than one way to solve each of these, but few are optimal
- State your assumptions
- We'll go through an example solution after you have a chance to try things yourselves
- Notes about the live stream
- If you have questions, raise your hand and I'll unmute you
- Alternatively, type your question in chat and I'll try to get to it.
Q1 [EASY]
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have a connected security system which will automatically contact the police if two adjacent houses are broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example:
Input: [1,2,3,1] Output: 4
Q2 [MEDIUM]
You are given a one dimensional array that may contain both positive and negative integers, find the sum of a contiguous subarray of numbers which has the largest sum.
For example, if the given array is [-2, -5, 6, -2, -3, 1, 5, -6], then the maximum subarray sum is 7.
You may assume that the array contains at least one positive integer.
Q3 [Medium]
A tourist visits Manhattan and wants to walk past as many attractions as possible. The streets of Manhattan form a perfect grid. The tourist starts in the NW corner and ends in the SE corner of the grid. The tourist can only move E and S. AT every intersection they can choose between two directions. In every street between two intersections are 0 or more attractions.
Maximize the sum of seen attractions from start to finish.
Assume you are given a matrix E where E[(x1,y1),(x2,y2)] = the number of attractions between intersections (x1,y1) and (x2,y2)
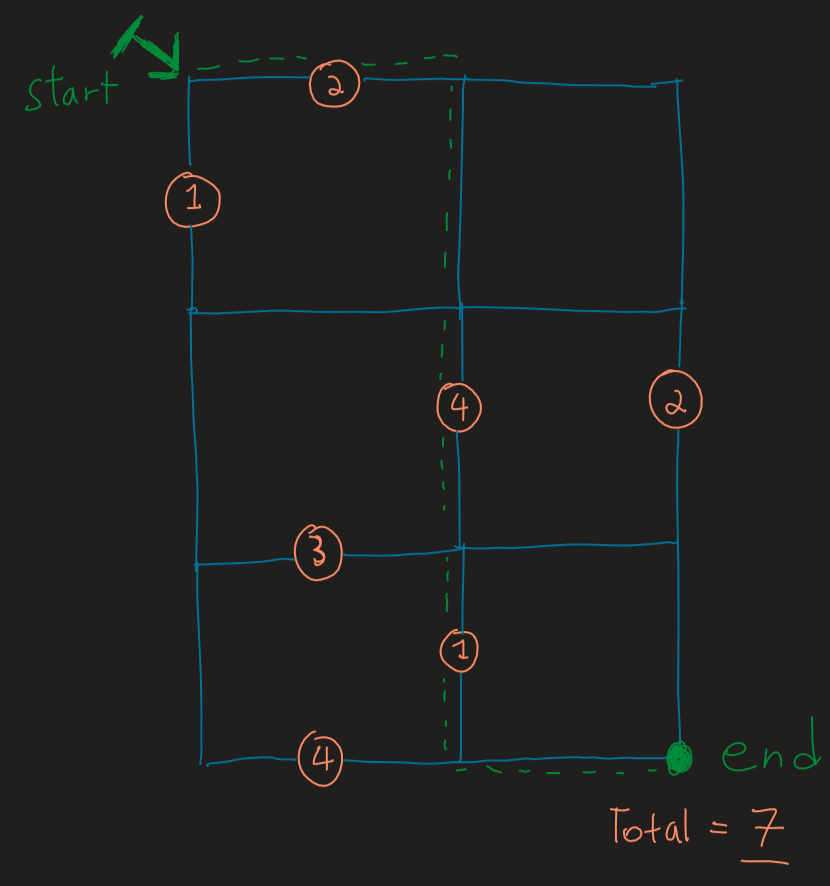
Q4 [Hard]
Given two sequences, find the length of longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous. For example, “abc”, “abg”, “bdf”, “aeg”, ‘”acefg”, etc. are all subsequences of “abcdefg”.
Examples:
LCS("ABCDGH", "AEDFHR") returns 3 ("ADH")
LCS("AGGTAB", "GXTXAYB") returns 4 ("GTAB")
Q5 [Medium]
Given a rod of length n inches and an array of prices that contains prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces.
For example, if length of the rod is 8 and the values of different pieces are given as following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6)
length | 1 2 3 4 5 6 7 8 -------------------------------------------- price | 1 5 8 9 10 17 17 20