Workshop Testing

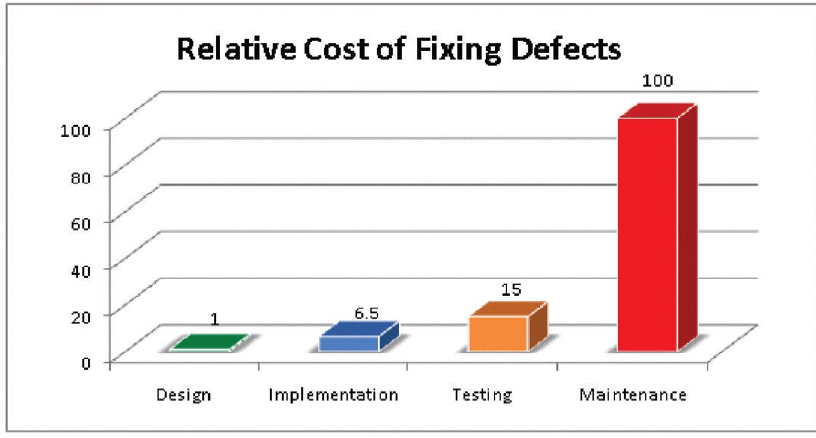
Why testing?

Find bugs
Prevent bugs
Requirements
Safes $$
Documentation (Contract)
Predictability, risk reduction, maintainability
Only well designed code can be tested
The list goes on and on

Test Driven Development

TDD = Test Driven Development

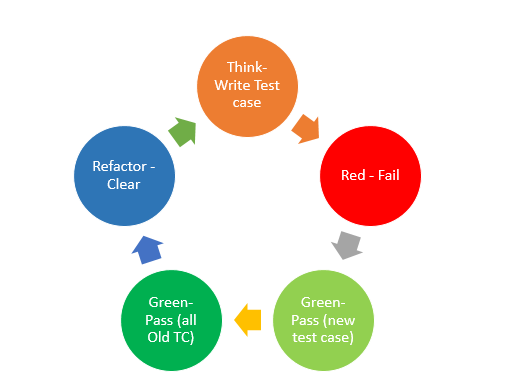
Test Driven Development

Testing Pyramide
- large base of unit tests,
- supported by a smaller layer of integration tests,
- with an even smaller layer of functional tests
Different approaches:
- Top to bottom or vice versa
  - It's a choice

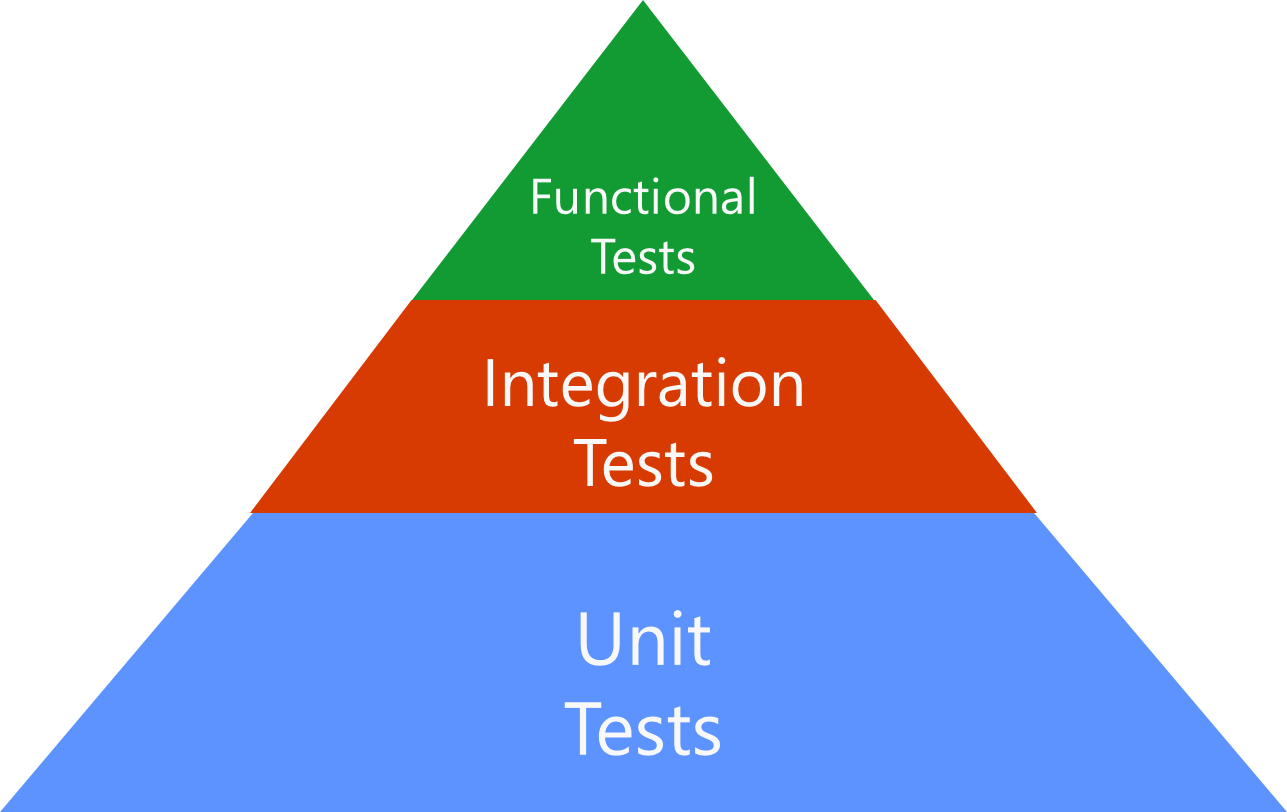
We will start here

Tools for Unit Testing

Tools:
- XUnit.net
- NUnit (good documentation)
- MSTest (never used it, maybe it's good)

Unit Test:
- only the public interface
- many tests, multiple tests for each public method (property)
- white box testing (we have the code, we should write it after the test, accordingly to TDD)

Let's start with a demo, TDD Unit Test

Tool: NUnit
Feature Request:
- Fibonacci sequence
- Next: add a stopwatch to measure performance

Demo take aways

Project structure
Multiple test cases
Naming Convention
- There are many

Arrange Act Assert

SUT = System Under Test (the method/class to test)
Arrange = setup/prepare the SUT for testing
Act = execute the test (method)
Assert = check if the result (return value) is what we expect
- 1 or multiple assertions

Naming Conventions Unit Tests

public void IsEven_NumberIsEven_False(int number, bool expected)
{

Lot's of possibilities:

It's a personal choice or/and project/company choice

Dependencies

If we use new or other hard code dependencies (from infrastructure for example), we can't test the unit in the Isolation
Solution: refactor the code, so it's testable
- Strange: we developed the code (TDD), so this could have never happened :-)

Dependencies

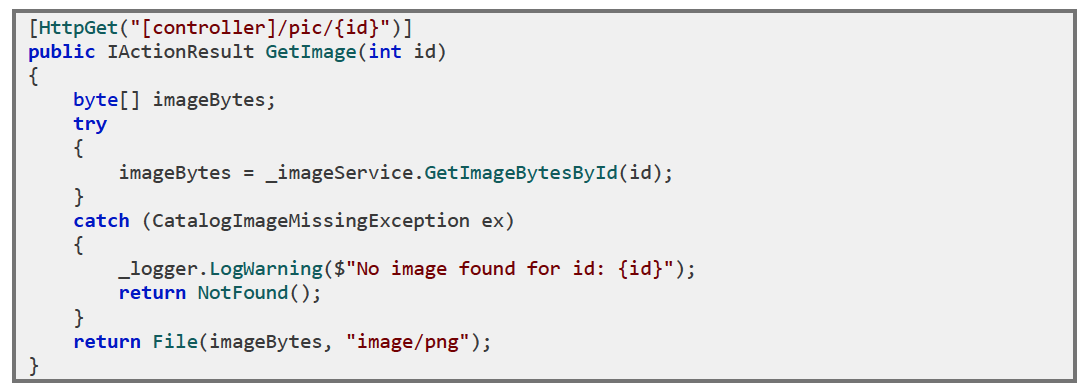
Refactor

Dependencies we can Mock

We test one unit (method), so we need to fake (mock) the rest
A --> IB, To test A we need to mock IB
Interfaces only
- Not really true, but this is the way to go!

Multiple libraries
- Moq, fakeiteasy, NSubstitute
  - It's easier to understand (syntax), my opinion

Mock (NSubstitute)

Clean mocking for unit tests using NSubstitute in .NET (Core, Framework, Standard)

Exercise

Feature Request:
- Make a IsLeapYear(int year) method
  - Write unit test (TDD Cycle)
  - Refactor code
- Next: add Logger dependency with Log(string message) method.
  - Mock/fake the Logger

Homework

Make a dart scoreboard
- I had a "hard time" understanding the requirements (there are some details, terminology, etc)
- YouTube
Let's review/discuss together
- Use multiple objects to build the system
- Use TDD
- Use mock framework (NSubstitute, Moq)

class Node {
  
}

public class Recursion
{
	// sum of n natural numbers
    // 1 + 2 + 3 + ... + n
    // for n = 5, the sum is 15, because 1 + 2 + 3 + 4 + 5 = 15
    public static int Sum(int n)
    {
        
    }
}

public class Recursion
{
	// sum of n natural numbers
    // 1 + 2 + 3 + ... + n
    // for n = 5, the sum is 15, because 1 + 2 + 3 + 4 + 5 = 15
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
    }
}

public class Recursion
{
	// sum of n natural numbers
    // 1 + 2 + 3 + ... + n
    // for n = 5, the sum is 15, because 1 + 2 + 3 + 4 + 5 = 15
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

public static void Main(String[] args) {
	Console.WriteLine(Recursion.Sum(3));
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

Sum(2)

2 + Sum(1)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1)

1 + Sum(0)

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1)

1 + Sum(0)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1)

1 + Sum(0)

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1)

1 + Sum(0)

Sum(0)

Sum(1)

1 + Sum(0)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1) = 1

1 + 0

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

2 + Sum(1)

Sum(2)

2 + Sum(1)

public class Recursion
{
    public static int Sum(int n)
    {
        if (n == 0) //base case
        {
            return 0;
        }
        else
        {
            return n + Sum(n - 1); //recursive case
        }
    }
}

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

Sum(3)

3 + Sum(2)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(2)

2 + Sum(1)

Sum(1) = 1

1 + 0

Sum(3)

= 3 + Sum(2)

= 3 + (2 + Sum(1))

= 3 + (2 + (1 + Sum(0)))

= 3 + (2 + (1 + (0)))

2 + Sum(1)

Sum(2)

2 + Sum(1)

Workshop Testing

Why testing?

Test Driven Development

Test Driven Development

Tools for Unit Testing

Let's start with a demo, TDD Unit Test

Demo take aways

Arrange Act Assert

Naming Conventions Unit Tests

Dependencies

Dependencies

Dependencies we can Mock

Mock (NSubstitute)

Clean mocking for unit tests using NSubstitute in .NET (Core, Framework, Standard)

Exercise

Homework