Un framework de código abierto para programar computadoras cuánticas

Cirq

Requisitos

Opción 1: Maquina local

¿Cómo se usa?

# Actualizamos pip
python -m pip install --upgrade pip

# Instalamos cirq
python -m pip install cirq

https://quantumai.google/cirq/start/install

Opción 1: Maquina local

Opción 2: Google Colab

¿Cómo se usa?

https://colab.research.google.com

Conceptos de Cirq

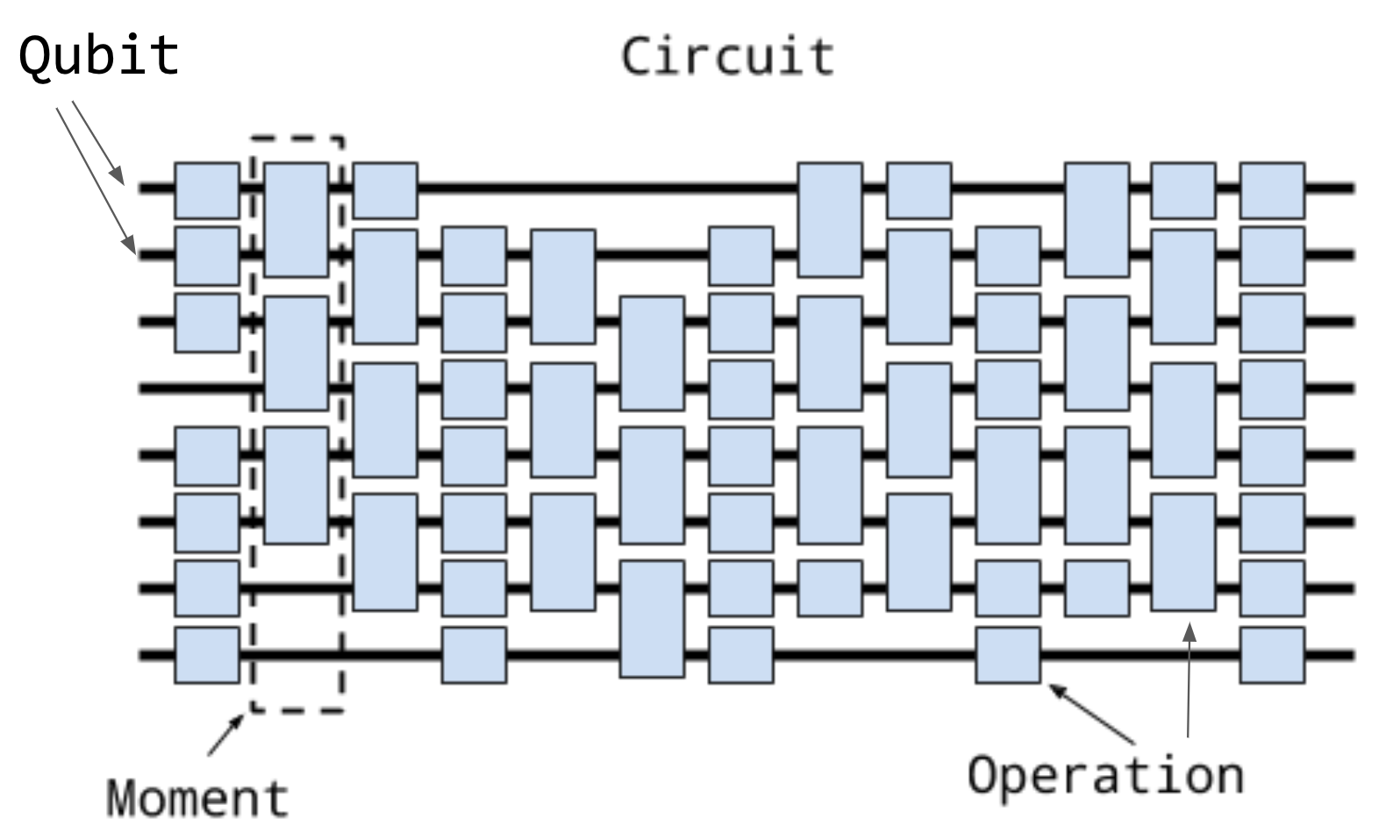
Qubit

Es la version cuántica de un bit.

Es la mínima unidad de información cúantica.

# Crear un qubit con indice `i`
cirq.q(i)
cirq.LineQubit(i)

# Crear un qubit con nombre `name`
cirq.q(name)

# Crear un conjunto de qubits desde `i` hasta `j`
# Usa los mismos parametros que range()
cirq.LineQubit.range(i, j)

# Un arreglo 2D cuadrado de n×n qubits,
# con desfasaje top y left opcionales.
cirq.GridQubit.square(n, top=0, left=0)

Qubit

Como crear un qubit es algo muy comun, crear la abreviacion cirq.q para varias configuraciones comunes (caso unidimencional y caso con nombre).

Los qubits utilizan la base computacional, y vienen inicializados en el estado 0.

Existe la posibilidad de crear arreglos bidimencionales. Sin embargo, como no vimos eso en la clase, no sera el foco de esta presentación

Operaciones

Las operaciones (generalmente asociadas a las puertas cuánticas), representan procesos físicos que le ocurren a un qubit.

# Creo 3 cubits
q0, q1, q2 = cirq.LineQubit.range(3)

# Compuerta NOT (aplicado al qubit 0)
cirq.X(q0)

# Compuerta CNOT (control: 1, target: 0)
cirq.CX(q1, q0)

# Mido el cubit 2
cirq.measure(q2)

# Aplico un corrimiento de fase respecto al eje Z
# de pi radianes al qubit 0 (utilizo pi de sympy)
cirq.rz(sympy.pi)(q0)

https://quantumai.google/cirq/build/gates#common_gates

Operaciones

Tambien se pueden construir compuertas propias a partir de matrices unitarias.

"""Define a custom gate with a parameter."""
class RotationGate(cirq.Gate):
    def __init__(self, theta):
        super(RotationGate, self)
        self.theta = theta

    def _num_qubits_(self):
        return 1

    def _unitary_(self):
        return np.array([
            [np.cos(self.theta), np.sin(self.theta)],
            [np.sin(self.theta), -np.cos(self.theta)]
        ]) / np.sqrt(2)

    def _circuit_diagram_info_(self, args):
        return f"R({self.theta})"

my_gate = RotationGate(sympy.pi)

R(\theta) = \frac{1}{\sqrt{2}} \left[ \begin{matrix} \cos \theta & \sin \theta \\ \sin \theta & - \cos \theta \end{matrix} \right]

Operaciones

Tambien se pueden construir a partir de descomposiciones de compuertas.

class MySwap(cirq.Gate):
    def __init__(self):
        super(MySwap, self)

    def _num_qubits_(self):
        return 2

    def _decompose_(self, qubits):
        a, b = qubits
        yield cirq.CNOT(a, b)
        yield cirq.CNOT(b, a)
        yield cirq.CNOT(a, b)

    def _circuit_diagram_info_(self, args):
        return ["CustomSWAP"] * self.num_qubits()

my_swap = MySwap()

# Output

0: ────CustomSWAP───
       │
1: ────CustomSWAP───

Momentos

Son colecciones de operaciones. Todas las operaciones de un momento deberían ejecutarse al mismo tiempo.

# Creamos dos qubits
q0, q1 = cirq.LineQubit.range(2)

# Creamos un momento donde a cada cubit se le aplica
# una compuerta NOT
moment = cirq.Moment([
  cirq.X(q0),
  cirq.H(q1)
])

# Imprimimos el momento
print(moment)

#   ╷ 0 1
# ╶─┼─────
# 0 │ X H
#   │

Circuitos

La estructura de mas alto nivel.

Son series ordenadas de momentos (el orden si importa)

# Creamos dos qubits
q0, q1 = cirq.LineQubit.range(2)

# Creamos dos momentos con operaciones
moment1 = cirq.Moment([cirq.X(q0), cirq.H(q1)])
moment2 = cirq.Moment(cirq.X(q1))

# Creamos el circuito con los dos momentos
circuit = cirq.Circuit([moment1, moment2])

# Imprimimos el circuito
print(circuit)

# Output
# 0: ───X───────
#
# 1: ───H───X───

Circuitos

# Creamos dos qubits
q0, q1 = cirq.LineQubit.range(2)

# Creamos un circuito vacio
circuit = cirq.Circuit()

# Agregamos un conjunto de operaciones
circuit.append([cirq.X(q0), cirq.H(q1)])

# Agregamos una sola operacion
circuit.append(cirq.X(q1))

# Imprimimos el circuito
print(circuit)

# Output
# 0: ───X───────
#
# 1: ───H───X───

# Creamos dos qubits
q0, q1 = cirq.LineQubit.range(2)

# Creamos un circuito vacio
circuit = cirq.Circuit()

# Agregamos una sola operacion
circuit.append(cirq.H(q1))

# Agregamos operaciones
circuit.append([cirq.X(q0), cirq.X(q1)])

# Imprimimos el circuito
print(circuit)

# Output
# 0: ───X───────
#
# 1: ───H───X───

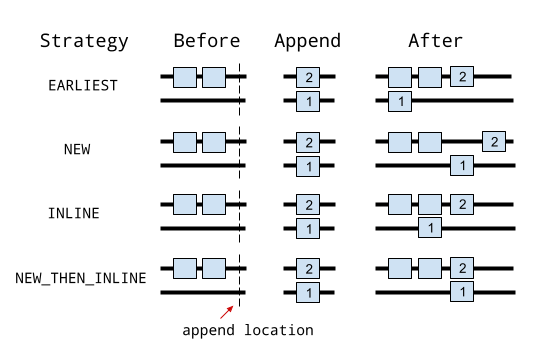
Circuitos

Estrategias de inserción

Simulador

# Creamos dos qubits
q0, q1 = cirq.LineQubit.range(2)

# Creamos un circuito
circuit = cirq.Circuit()

# Le agregamos operaciones
circuit.append([cirq.X(q0), cirq.H(q1), cirq.X(q1)])

# Le agregamos mediciones
circuit.append([cirq.measure(q0), cirq.measure(q1)])

# Imprimimos el circuito
print(circuit)

# Output
# 0: ───X───M───────
# 
# 1: ───H───X───M───

# Creamos un simulador
# (OPCIONAL): se le pone una seed para
# reproducibilidad
simulator = cirq.Simulator(seed=0)

# Simulamos el circuito
result = simulator.run(circuit,
                      repetitions=1)

# Imprimimos el resultado
print(result)

# Output
# q(0)=1
# q(1)=1

Simulaciones exactas

Simulador

# Creamos un simulador y simulamos el circuito
simulator = cirq.Simulator(seed=0)
result = simulator.simulate(circuit, qubit_order=[q0, q1])

# Imprimimos el resultado
print(result)

# Output
# measurements: (no measurements)
#
# qubits: (cirq.LineQubit(0),)
# output vector: |1⟩
#
# qubits: (cirq.LineQubit(1),)
# output vector: 0.707|0⟩ + 0.707|1⟩
#
# phase:
# output vector: |⟩

Accediendo al ket de estado

Simulador

# Usamos el mismo circuito de antes
 
# Creamos un simulador y simulamos el circuito
simulator = cirq.Simulator(seed=0)

steps = simulator.simulate_moment_steps(circuit, qubit_order=[q0, q1])

for i, step in enumerate(steps):
  print(f'state at step {i}: {step.dirac_notation()}')
print(f'Mediciones finales: {step.measurements}')

# Output
# state at step 0: 0.71|10⟩ + 0.71|11⟩
# state at step 1: 0.71|10⟩ + 0.71|11⟩
# state at step 2: |11⟩
# Mediciones finales: {'q(0)': [1], 'q(1)': [1]}

Paso a paso