Taller
¡Bienvenidos!

Fase 1: Introducción
- Instalación y entornos de desarrollo
- Ecosistema de Julia
¿0.6 o +1.0?
versión
Instalación y entornos de desarrollo
Ubuntu:
sudo add-apt-repository ppa:staticfloat/juliareleases
sudo add-apt-repository ppa:staticfloat/julia-deps
sudo apt-get update
sudo apt-get install julia
Fedora:
sudo dnf copr enable nalimilan/julia
sudo yum install juliaVarias opciones:
a) Binarios:
http://julialang.org/downloads/
b) Manejador de paquetes
c) Compilación del codigo fuente
https://github.com/JuliaLang/julia
d) IJulia: Julia en el navegador web (local)
e) Uso en linea:
$ julia
_
_ _ _(_)_ | A fresh approach to technical computing
(_) | (_) (_) | Documentation: http://docs.julialang.org
_ _ _| |_ __ _ | Type "?help" for help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 0.4.0-dev+6859 (2015-08-20 19:38 UTC)
_/ |\__'_|_|_|\__'_| | Commit 92ddae7 (55 days old master)
|__/ | x86_64-w64-mingw32
julia> println("hello world")Instalación y entornos de desarrollo
Instalación y entornos de desarrollo
-
Vim: julia-vim
-
Emacs: marcado de la sintaxis de julia gracias a este paquete.
-
Sublime Text: Sublime-IJulia integra a IJulia dentro Sublime Text -la instalacion es algo compleja pero vale la pena.
-
Notepad++: soporte de sintaxis mediante un archivo de configuración
-
Light Table: soporte a Julia mediante el proyecto Juno (solo hasta la version 0.3.11).
-
Atom: IDE oficial para la version 0.4
Ecosistema de Julia
Documentación:
Cheat Sheets:
https://juliadocs.github.io/Julia-Cheat-Sheet/
http://math.mit.edu/~stevenj/Julia-cheatsheet.pdf
Packages oficiales:
El secreto mejor guardado: Awesome Julia
WTF!
¿Y los if y for's pa' cuándo?
¿Por qué carajos necesito saber todo esto?
Fase 2: Instrucciones básicas
- Aritmética enteros, Flotantes, complejos
- Variables
- Condicionales
- Iteraciones
- Funciones matemáticas
- Funciones
Aritmética
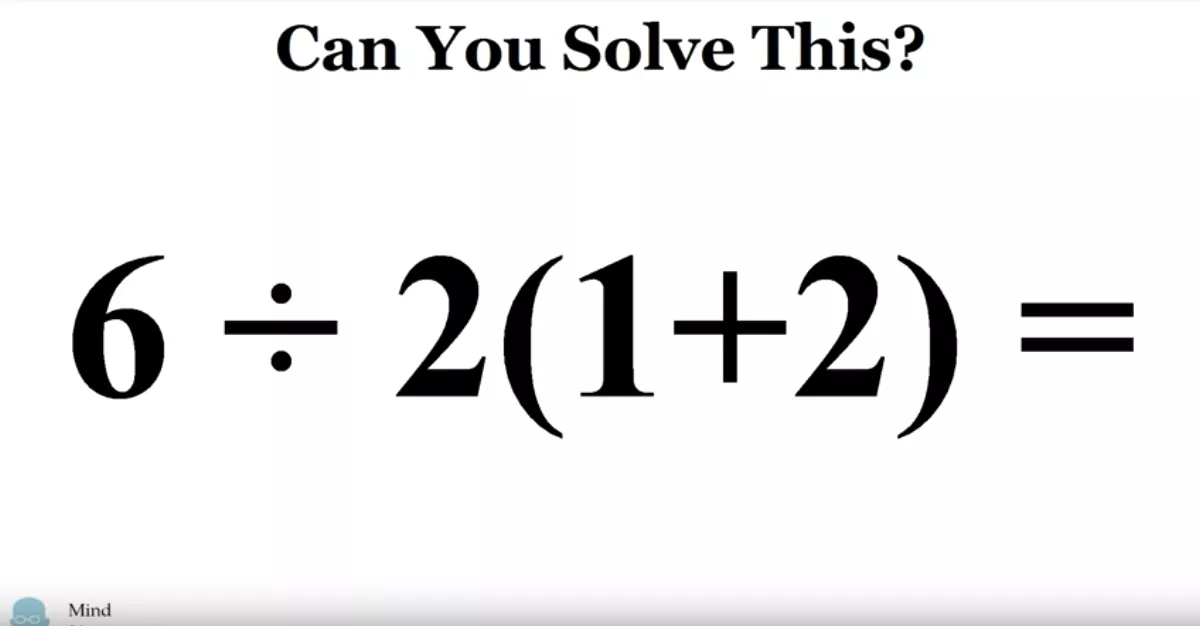
¡Vamos a crear el árbol sintáctico!
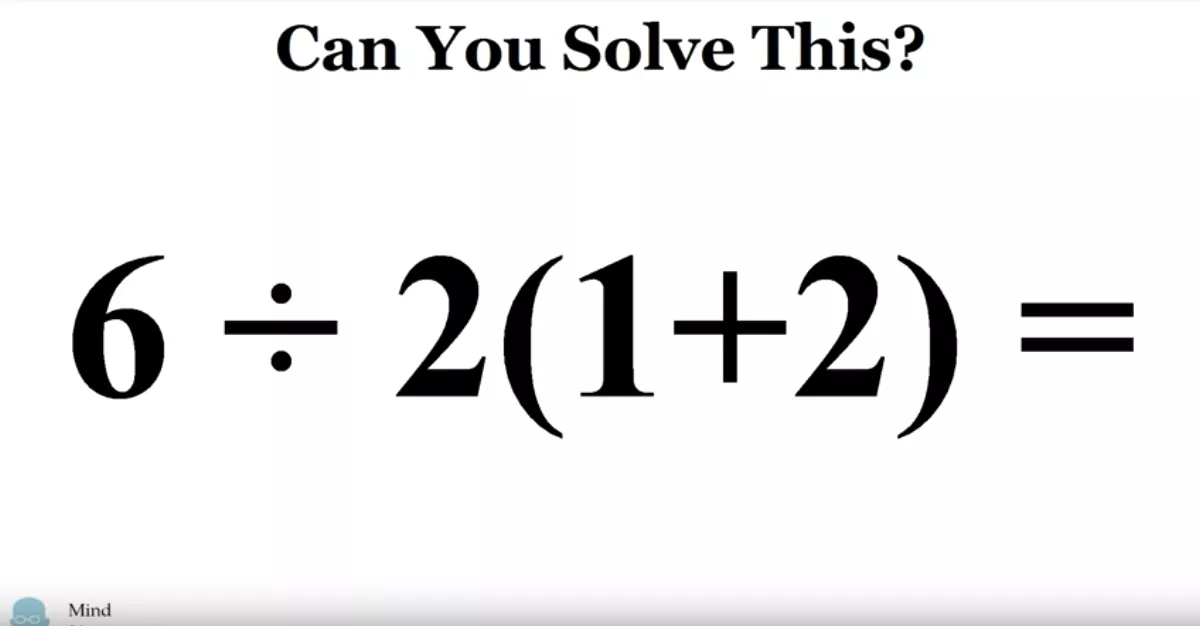
Variables
julia> m = 2.32
2.32
julia> m
2.32
julia> ❄ = -12
-12
julia> ✹ = 27
27
julia> ❄ > ✹
false
julia> π
π = 3.1415926535897...
julia> π = 3.2
Warning: imported binding for π overwritten in module Main
3
julia> π
3.2Variables
¡Convenciones!

Condicionales
Loops
Funciones matemáticas
Raíz cuadrada, exponente, seno, coseno, etc
Funciones
Fase 3: Estructuras de datos
- Arreglos
- diccionarios
- tuplas
- matrices
ARREGLOS
function printsum(a)
# summary generates a summary of an object
println(summary(a), ": ", repr(a))
end
# arrays can be initialised directly:
a1 = [1,2,3]
printsum(a1)
#> 3-element Array{Int64,1}: [1,2,3]
# or initialised empty:
a2 = []
printsum(a2)
#> 0-element Array{None,1}: None[]
# since this array has no type, functions like push! (see below) don't work
# instead arrays can be initialised with a type:
a3 = Int64[]
printsum(a3)
#> 0-element Array{Int64,1}: []
# ranges are different from arrays:
a4 = 1:20
printsum(a4)
#> 20-element UnitRange{Int64}: 1:20
# however they can be used to create arrays thus:
a4 = [1:20]
printsum(a4)
#> 20-element Array{Int64,1}: [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
# arrays can also be generated from comprehensions:
a5 = [2^i for i = 1:10]
printsum(a5)
#> 10-element Array{Int64,1}: [2,4,8,16,32,64,128,256,512,1024]
# arrays can be any type, so arrays of arrays can be created:
a6 = (Array{Int64, 1})[]
printsum(a6)
#> 0-element Array{Array{Int64,1},1}: []
# (note this is a "jagged array" (i.e., an array of arrays), not a multidimensional array, these are not covered here)
# Julia provided a number of "Dequeue" functions, the most common for appending to the end of arrays is push!
# ! at the end of a function name indicates that the first argument is updated.
push!(a1, 4)
printsum(a1)
#> 4-element Array{Int64,1}: [1,2,3,4]
# push!(a2, 1) would cause error:
push!(a3, 1)
printsum(a3) #> 1-element Array{Int64,1}: [1]
#> 1-element Array{Int64,1}: [1]
push!(a6, [1,2,3])
printsum(a6)
#> 1-element Array{Array{Int64,1},1}: [[1,2,3]]
# using repeat() to create arrays
# you must use the keywords "inner" and "outer"
# all arguments must be arrays (not ranges)
a7 = repeat(a1,inner=[2],outer=[1])
printsum(a7)
#> 8-element Array{Int64,1}: [1,1,2,2,3,3,4,4]
a8 = repeat([4:-1:1],inner=[1],outer=[2])
printsum(a8)
#> 8-element Array{Int64,1}: [4,3,2,1,4,3,2,1]DICCIONARIOS
# dicts can be initialised directly:
a1 = {1=>"one", 2=>"two"}
printsum(a1) #> Dict{Any,Any}: {2=>"two",1=>"one"}
# then added to:
a1[3]="three"
printsum(a1) #> Dict{Any,Any}: {2=>"two",3=>"three",1=>"one"}
# (note dicts cannot be assumed to keep their original order)
# dicts may also be created with the type explicitly set
a2 = Dict{Int64, String}()
a2[0]="zero"
# dicts, like arrays, may also be created from comprehensions
a3 = {i => @sprintf("%d", i) for i = 1:10}
printsum(a3)#> Dict{Any,Any}: {5=>"5",4=>"4",6=>"6",7=>"7",2=>"2",10=>"10",9=>"9",8=>"8",3=>"3",1=>"1"}
# as you would expect, Julia comes with all the normal helper functions
# for dicts, e.g., (haskey)[http://docs.julialang.org/en/latest/stdlib/base/#Base.haskey]
println(haskey(a1,1)) #> true
# which is equivalent to
println(1 in keys(a1)) #> true
# where keys creates an iterator over the keys of the dictionary
# similar to keys, (values)[http://docs.julialang.org/en/latest/stdlib/base/#Base.values] get iterators over the dict's values:
printsum(values(a1)) #> ValueIterator{Dict{Any,Any}}: ValueIterator{Dict{Any,Any}}({2=>"two",3=>"three",1=>"one"})
# use collect to get an array:
printsum(collect(values(a1)))#> 3-element Array{Any,1}: {"two","three","one"}MATRICES
# repeat can be useful to expand a grid
# as in R's expand.grid() function:
m1 = hcat(repeat([1:2],inner=[1],outer=[3*2]),
repeat([1:3],inner=[2],outer=[2]),
repeat([1:4],inner=[3],outer=[1]))
printsum(m1)
#> 12x3 Array{Int64,2}: [1 1 1
#> 2 1 1
#> 1 2 1
#> 2 2 2
#> 1 3 2
#> 2 3 2
#> 1 1 3
#> 2 1 3
#> 1 2 3
#> 2 2 4
#> 1 3 4
#> 2 3 4]
# for simple repetitions of arrays,
# use repmat
m2 = repmat(m1,1,2) # replicate a9 once into dim1 and twice into dim2
println("size: ", size(m2))
#> size: (12,6)
m3 = repmat(m1,2,1) # replicate a9 twice into dim1 and once into dim2
println("size: ", size(m3))
#> size: (24,3)
# Julia comprehensions are another way to easily create
# multidimensional arrays
m4 = [i+j+k for i=1:2, j=1:3, k=1:2] # creates a 2x3x2 array of Int64
m5 = ["Hi Im # $(i+2*(j-1 + 3*(k-1)))" for i=1:2, j=1:3, k=1:2] # expressions are very flexible
# you can specify the type of the array by just
# placing it in front of the expression
m5 = ASCIIString["Hi Im element # $(i+2*(j-1 + 3*(k-1)))" for i=1:2, j=1:3, k=1:2]
printsum(m5)
#> 2x3x2 Array{ASCIIString,3}: ASCIIString["Hi Im element # 1" "Hi Im element # 3" "Hi Im element # 5"
#> "Hi Im element # 2" "Hi Im element # 4" "Hi Im element # 6"]
#>
#> ASCIIString["Hi Im element # 7" "Hi Im element # 9" "Hi Im element # 11"
#> "Hi Im element # 8" "Hi Im element # 10" "Hi Im element # 12"]
# Array reductions
# many functions in Julia have an array method
# to be applied to specific dimensions of an array:
sum(m4,3) # takes the sum over the third dimension
sum(m4,(1,3)) # sum over first and third dim
maximum(m4,2) # find the max elt along dim 2
findmax(m4,3) # find the max elt and its index along dim 2 (available only in very recent Julia versions)
# Broadcasting
# when you combine arrays of different sizes in an operation,
# an attempt is made to "spread" or "broadcast" the smaller array
# so that the sizes match up. broadcast operators are preceded by a dot:
m4 .+ 3 # add 3 to all elements
m4 .+ [1:2] # adds vector [1,2] to all elements along first dim
# slices and views
m4[:,:,1] # holds dim 3 fixed and displays the resulting view
m4[:,2,:] # that's a 2x1x2 array. not very intuititive to look at
# get rid of dimensions with size 1:
squeeze(m4[:,2,:],2) # that's better
# assign new values to a certain view
m4[:,:,1] = rand(1:6,2,3)
printsum(m4)
#> 2x3x2 Array{Int64,3}: [3 5 2
#> 2 2 2]
#>
#> [4 5 6
#> 5 6 7]
# (for more examples of try, catch see Error Handling above)
try
# this will cause an error, you have to assign the correct type
m4[:,:,1] = rand(2,3)
catch err
println(err)
end
#> InexactError()
try
# this will cause an error, you have to assign the right shape
m4[:,:,1] = rand(1:6,3,2)
catch err
println(err)
end
#> DimensionMismatch("tried to assign 3x2 array to 2x3x1 destination")