TIPE
|
Amortisseur réglable : une solution innovante pour les systèmes parasismiques |


1
2016-2018
2
Rapport avec le thème :
Milieux : interactions, interfaces, homogénéité, ruptures

Etudier l'amplitude du système au travers d'une étude fréquentielle lors d'une perturbation sinusoïdale créée par une table réalisant des mouvements de translation
Objectif de l'étude :
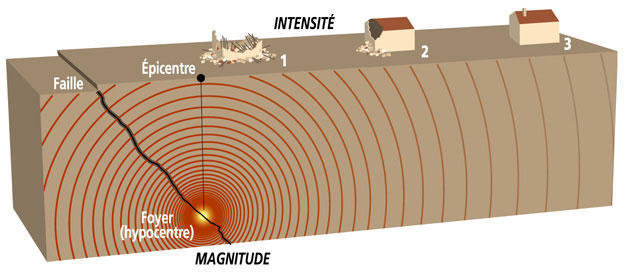
I. Présentation du support expérimental
II. Modélisation du comportement dynamique
III. Expérimentation
SOMMAIRE
3
- Table d’excitation à fréquence variable
- Possession capteurs et éléments structurels
- Support facile à adapter
1/ Simulation d'un séisme

Fréquence max : 5,8 Hz
Fréquence min : 1,7 Hz
4
I. Présentation du système
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
- Mise en place des plaques d'acier sur la maquette du pont Flaubert
- Modélisation du bâtiment de part la disposition de plaques en bois
- Fixation des amortisseurs
2/ Modélisation d'un bâtiment
25 cm
27 cm
Protocole
5

Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
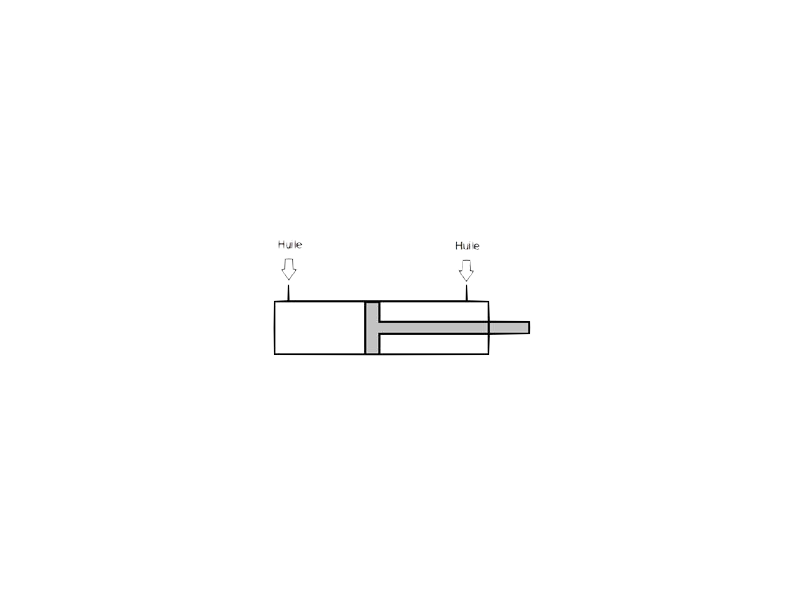
Amortisseurs réglables

120mm
Possibilité de changer l'huile de l'amortisseur
-> Il n'y a pas de ressort
6



Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
1 1cP = 1 mPa s


3/ Acquisition des informations
Accéléromètre étage
Accéléromètre tablier
Carte arduino
7





Acquérir
Traiter
Communiquer
Chaîne d'information
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Mesure des accélérations sur une plage de +3g
Mesure des accélérations de pesanteur
Mesure l'accélération dynamique résultant de vibrations

- Accéléromètre (x2)
8
- Programmes python
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Réception des données
Fonction lissage
9
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Détermination du module
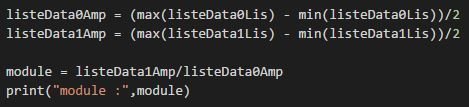
Détermination de la période

Détermination du retard
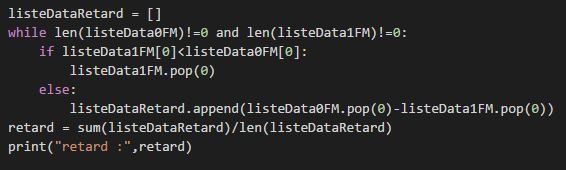

- Programmes python
II/ Etude théorique
kθ
-λv
O
x
θ
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
10
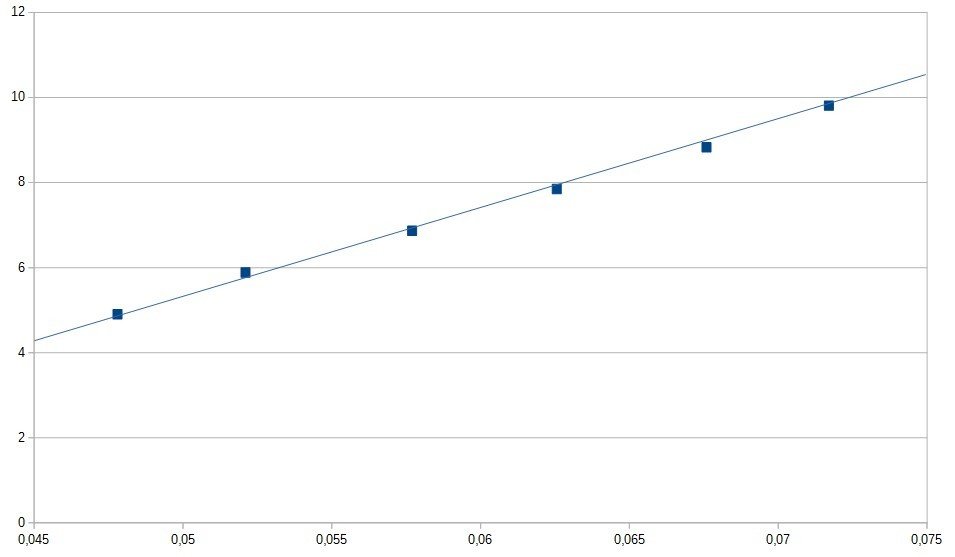
1/ Détermination du coefficient de rigidité de l'acier

Protocole :
Application d'une force au niveau du 2ème étage
Calcul de l'angle de déformation
11
θ
F=
kθ

Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
2
k/2 = 204 + 11 N/rad
12
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
F(N)
θ(rad)
2/ Détermination du coefficient de viscosité d'amortissement de l'amortisseur

Experience
amortisseur
masse
Logiciel de pointage Tracker
13
F=-λx
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Protocole :
Application d'une force sur l'amortisseur
Calcul de la vitesse de compression
X
400 cP
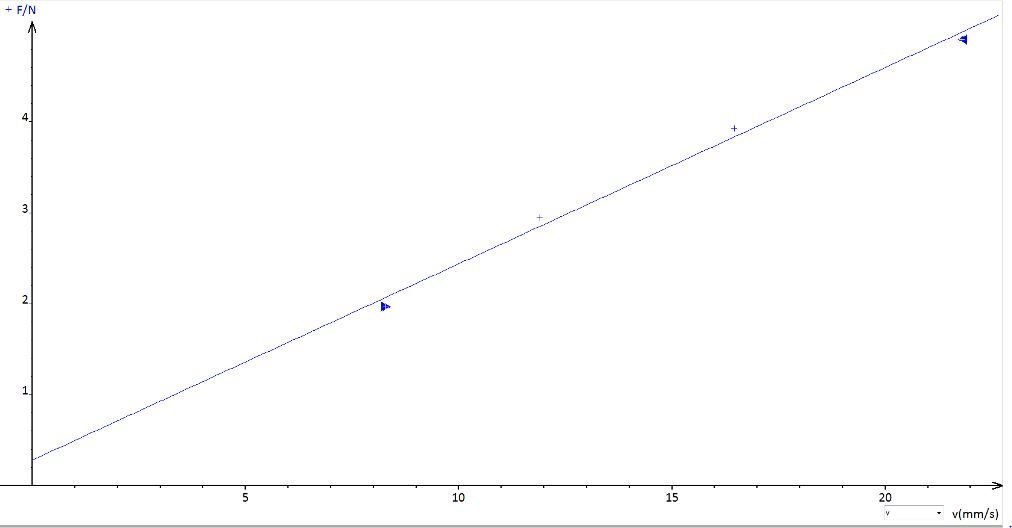
λ = 216 N.m.s
0.0083
200g
300g
400g
500g
0.0119
0.0165
0.0218
v(m/s)
F(N)
1.962
2.943
3.924
4.905
masse (g)
Même expérience pour chaque huile :
| 200 | 400 | 600 | |
|---|---|---|---|
| 58 | 216 | 354 |
14
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Viscosité
λ (N.m.s)
-1
-1
3/ Dynamique
15
Système : {Plaque à l'étage}
Bilan des forces :
P = -mgz
Fp =

kθ
-λx
O
x
θ
z
Équation résultante du Principe fondamental de la dynamique projetée sur x :
mx + + = 0
L
Fa
P
Fp
x
2
λx
kx
L
x
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
kθ
Fa=-λ(cos(α)xx+sin(α)zz)
α
λxx
4L
16
ω
k
Lm
ζ =
λ L
4 km
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Identification
Applications numériques :
200 cP :
ζ = 0,37
400 cP :
ζ = 1,39
600 cP :
ζ = 2,28
=
0
ω
0
=
38.9 + 8,6 rad/s
III/ Etude fréquentielle
17
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Text
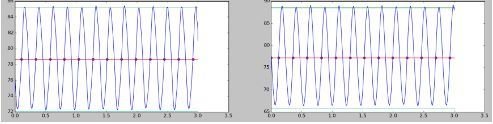
A vide
module : 1.57
période : 0.35 s
retard : -0.37 s
module : 7.45
période : 0.20 s
retard : -1.13 s
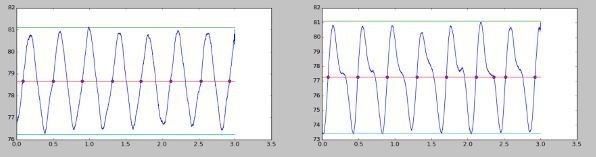
Effet de la variation de la fréquence sur le système
200 tr/min
350 tr/min
III/ Etude fréquentielle
18
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
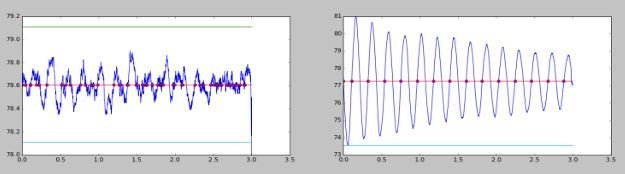
Text
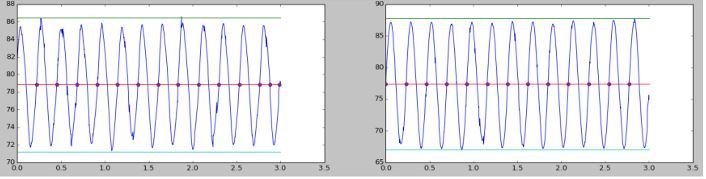
200 cP
module : 0.99
période : 0.40 s
retard : -0.39 s
module : 1.72
période : 0.22 s
retard : -0.01 s

Effet de la variation de la fréquence sur le système
200 tr/min
350 tr/min
III/ Etude fréquentielle
19
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Text
400 cP
module : 1.03
période : 0.25 s
retard : -0.20 s
module : 1.35
période : 0.23 s
retard : -0.01 s
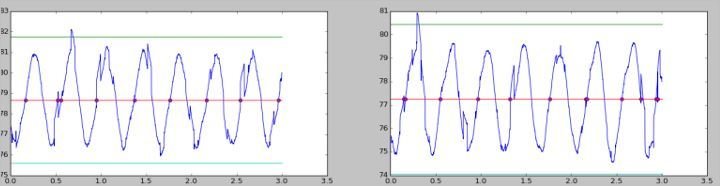
Effet de la variation de la fréquence sur le système
200 tr/min
350 tr/min
III/ Etude fréquentielle
20
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Quand f :
Vs : Amplitude de déformation de l'étage
Ve : Amplitude de déformation de la plaque
De plus on remarque que l'augmentation de la viscosité du fluide au sein de l'amortisseur permet de mieux amortir les variations d'amplitude
T
Vs
Ve
Tr
T
Effet de la variation de la fréquence sur le système
III/ Etude fréquentielle
21
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
Diagramme de Bode en gain (dB)
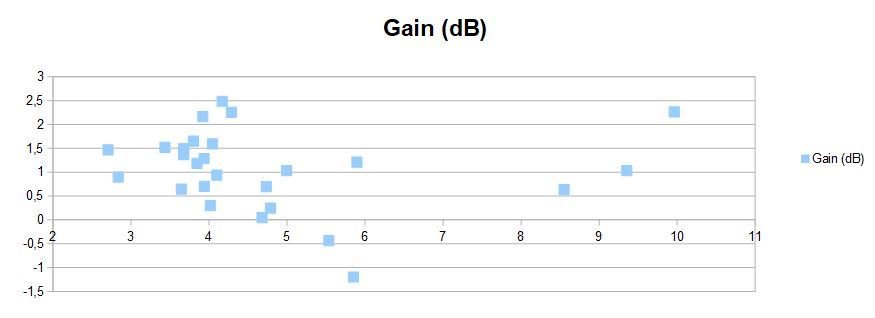
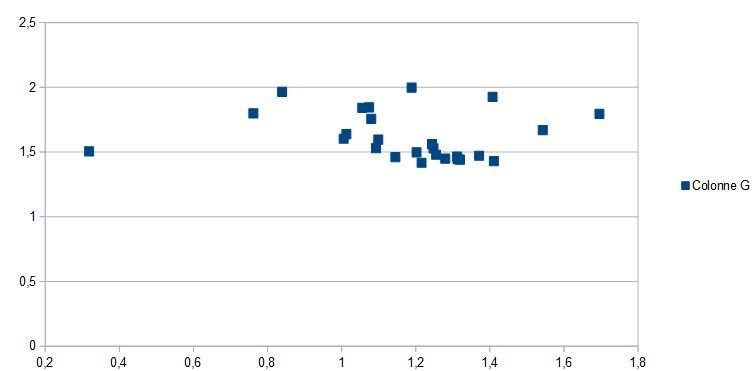
Remarque: Pour deux mêmes mesures les accéléromètres renvoyaient des modules différents, de plus la plage de fréquence proposée par le Pont Flaubert n'est pas suffisante, c'est pourquoi le tracé du diagramme de Bode n'est pas satisfaisant
L'augmentation de la viscosité permet d'atténuer les variations d'amplitude
Tracé du diagramme de Bode
22
Présentation du système
Etude théorique
Etude expérimentale
Séisme
Bâtiment
Informations
λ
k
Dynamique
Etude fréquentielle
CONCLUSION
|
|
|---|
ζ
D'après l'étude théorique :
Plus λ augmente plus ζ augmente
Régime privilégié :
apériodique ( ζ > )
1
2
200CP :
400CP :
600CP :
ζ = 0,37
ζ =1,39
ζ=2.28
ω
D'après l'étude théorique :
ω =38,9 + 8,6 rad/s
D'après l'étude expérimentale :
ω =32,4 rad/s
0
0
0