Método Secante

Análisis Numerico

8 Sep, 2015

¿ Que es una secante ?

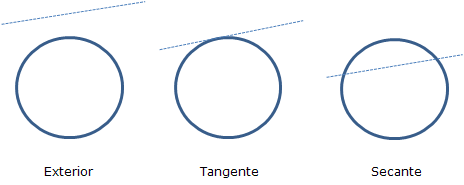
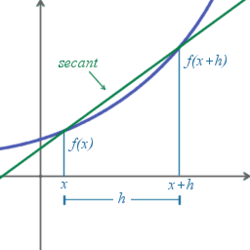
Método secante

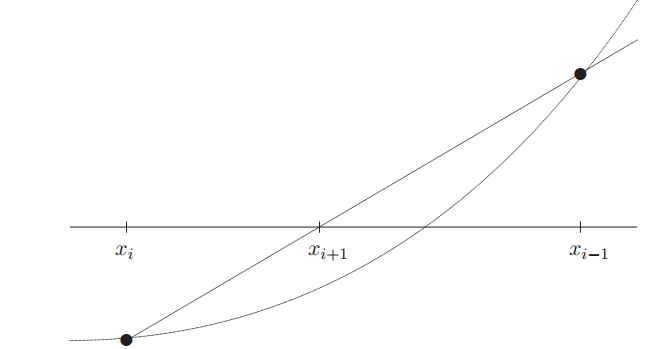
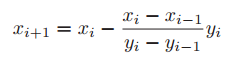
El método de la secante requiere dos aproximaciones iniciales x0 y x1

Se continua haciendo iteraciones con cada uno de los puntos

Algoritmo

1. Seleccionar 2 puntos iniciales
2. Calcular recta que pasa por esos 2 puntos
3. El corte con el eje de las abscisas sera el nuevo punto
4. Volver a calcular la recta
5. Detenerse hasta hallar mínimo error o aprox a 0.

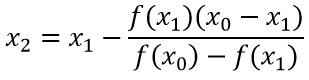
Calculo del nuevo punto

% Metodo secante
clear, clc
cf = input('Funcion:');
f = inline(cf);
x0 = input('Valor x0:');
x1 = input('Valor x1:');
lim = 0.000;
e = 100;
n = 0;
fprintf('n    x0    x1       x2      Error\n');

while(e > lim)
    
    x2 = x1 - (x1-x0)*f(x1)/(f(x1)-f(x0));
    e = abs(f(x2));
    fprintf('%i  %4.4f  %4.4f  %4.4f  %4.4f\n',n, x0,x1,x2,e);
    x0 = x1;
    x1 = x2;
    n = n+1;
  
end

Demo 2

Preguntas ?