資結囉
先來點簡單的
前綴(和)
- 定義 \(p_i\)為前\(i\)個東西的和。即$$p_i = \sum_{j = 0}^{i} a_j$$
- 任何一個區間都可以用兩個區間相減表示(區間本身是前綴例外)$$[i, j] = p_j - p_{i - 1}$$
差分
- 定義\(d_i\)代表第\(i\)項和第\(i - 1\)項的差,即$$d_i = a_i - a_{i - 1}$$,且\(d_0 = a_0\)
- 差分後,可得\(a_i = \sum_{j = 0}^i d_j\)
- 差分跟前綴互為逆運算(差分的前綴或前綴的差分會得到原序列
那可以用在哪裡呢?
其實隨時都可以用
Good Subarrays
給你一個長度\(n\)的序列,求出有多少對\(i \leq j\),使得\(a_i + ... + a_j = j - i + 1\)。
\(n \leq 10^5\)
Non-zero Segments
給你一個長度\(n\)的序列,求出最少需要插入幾個數字(任意數值)才能使序列中沒有區間和為\(0\)的子區間。
\(n \leq 2*10^5, a_i \neq 0\)
給你一個長度\(n\)的序列,有\(m\)筆操作,每次選定一個區間,將奇數項(由該區間開始編號)加上\(x\)和將偶數項扣掉\(x\),問最後序列的長相
\(n, m \leq 10^6\)
基本線段樹
Segment Tree
麻煩的問題
給你一個序列,支援兩種操作:
-
改變一個元素的值
-
求出某個區間的總和
好像沒有什麼好方法維護?
如果我們可以維護一些區間的答案
給你一個序列,支援兩種操作:
-
改變一個元素的值
-
求出某個區間的總和
好像沒有什麼好方法維護?(其實有啦w
把一個區間的和拆成好幾塊
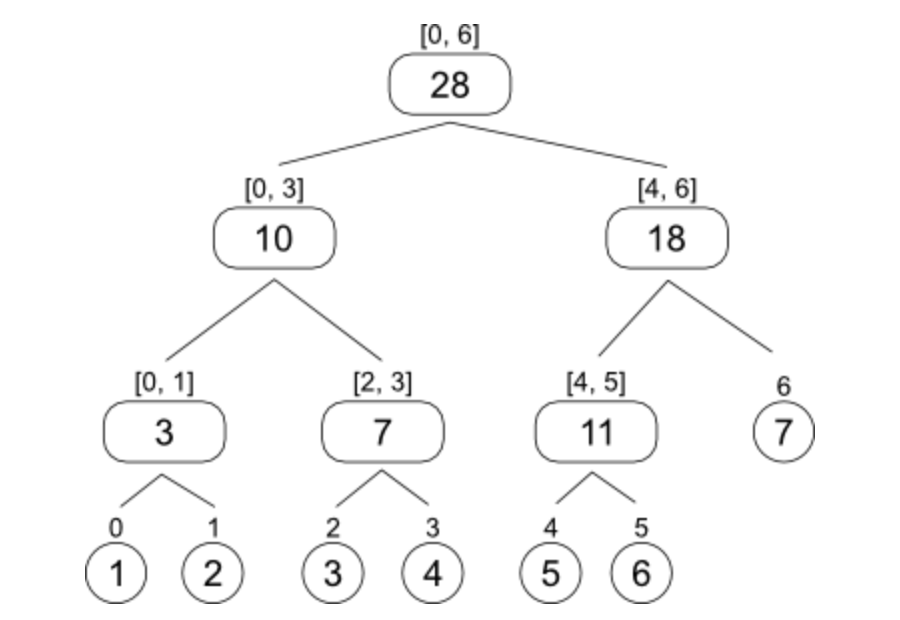
假設我們要找\([2, 6]\)的話...
線段樹—每個節點存區間的樹

- 線段樹是一顆二元樹,每個節點維護著某區間的答案。
- 兩個子節點維護的區間是原區間切一半之後的左右兩邊。
- 由於將長度為 \(n\)的區間一直切一半可以切\(logn\)次,故深度為\(O(logn)\)
實作方式
-
陣列型(最好寫、空間小)
-
指標型(算好寫、可以處理持久化和動態開點、空間肥)
-
偽指標型(只有 \(Wiwihorz\)會寫的毒瘤)
#include <iostream>
#include <algorithm>
#define ll long long
#define maxn 100005
using namespace std;
int seg[4 * maxn];
int main() {
}cur
2*cur
2*cur + 1
陣列型線段樹:
根節點編號\(1\),對大小為\(n\)的序列需要\(4 \times hbit(n)\)個節點位置
單點修改操作

每次往下走一層,複雜度\(O(logn)\)
0. 如果該節點區間為空,直接 return 掉
- 如果該節點紀錄的區間只有那個點,更新完該點答案後 return
- 否則判斷要修改的點是在左邊還是右邊遞迴下去,最後更新原節點答案
int seg[4 * maxn];
void modify(int cur, int l, int r, int ind, int val) {
if (r <= l) return;
if (r - l == 1 && l == ind) {
seg[cur] += val;
return;
}
int mid = (l + r) / 2;
if (ind < mid) modify(cur * 2, l, mid, ind, val);
else modify(cur * 2 + 1, mid, r, ind, val);
seg[cur] = seg[cur * 2] + seg[cur * 2 + 1];
}區間查詢操作

0. 如果該節點區間為空或是不包含詢問區間,直接 return 掉
- 如果查詢區間包含當前節點的整個區間,回傳該節點紀錄的答案
- 否則回傳左右子節點的合併結果
int query(int cur, int l, int r, int ql, int qr) {
if (r <= l || ql >= r || qr <= l) return 0;
if (ql <= l && qr >= r) {
return seg[cur];
}
int mid = (l + r) / 2;
return query(cur * 2, l, mid, ql, qr) + \
query(cur * 2 + 1, mid, r, ql, qr);
}每次查詢只會查到\(logn\)塊?

度
線段樹也可以拿來存
各種東西的答案
-
ex. 最大值,最小值
- 最大區間連續和
- 矩陣
- ...
基本進階線段樹
Basic Lazy Tag on Segment Tree
假設我要區間加值又區間求和呢?
總不能分成一堆單點加值來弄吧?
有沒有辦法懶一點
我懶
對每個節點多紀錄一個「懶惰標記 Lazy tag」,代表目前加到那裡的答案。
在修改時只動到修改的區間,查詢時順帶資訊
cur
2*cur
2*cur + 1
話說懶標其實有兩種
- 不用下推操作的
(\(seg[cur]\)代表當前節點經過子節點修改後的答案
- 需要下推操作的
該節點的懶標對\(seg[cur]\)做事,遇到的時候再處理。
這份講義會先討論第一種
設定懶標的流程(區間修改)
跟區間查詢的程式碼類似
0. 如果該節點區間為空或是不包含修改區間,直接 return 掉
- 如果查詢區間包含當前節點的整個區間,在這個區間的懶標上做修改操作
- 否則對左右子節點遞迴修改並且更新當前的答案
3
3
3
[1, 2)
[2, 3)
[3, 5)
6
3
6
12
操作:
把[1, 5)的每一項東西加上 3
稍微整理一下
-
剛剛的懶標\(lazy[cur]\)紀錄的是「這個區間的每個東西被加到多少」
-
\(seg[cur]\)在更新時要記得把子節點的長度考慮進去
#include <iostream>
#include <algorithm>
#define maxn 100005
using namespace std;
int seg[4 * maxn], lazy[4 * maxn];
void modify(int cur, int l, int r, int ql, int qr, int val) {
if (r <= l || ql >= r || qr <= l) return;
if (ql <= l && qr >= r) {
lazy[cur] += val;
return;
}
int mid = (l + r) / 2;
modify(cur * 2, l, mid, ql, qr, val);
modify(cur * 2 + 1, mid, r, ql, qr, val);
seg[cur] = seg[cur * 2] + (mid - l) * lazy[cur * 2] + \
seg[cur * 2 + 1] + (r - mid) * lazy[cur * 2 + 1];
}區間查詢現在要怎麼做呢
0. 如果該節點區間為空或是不包含修改區間,直接 return 掉
- 如果查詢區間包含當前節點的整個區間,回傳該節點紀錄的值加上懶標
- 否則對左右子節點遞迴查詢,並且加上當前節點懶標且合併答案
0 + 3
3
3
[3, 4)
[2, 3)
[3, 5)
6
3
6
12
操作:
查詢[2, 4)的
總和
+3
int query(int cur, int l, int r, int ql, int qr) {
if (r <= l || ql >= r || qr <= l) return 0;
if (ql <= l && qr >= r) {
return seg[cur] + (r - l) * lazy[cur];
}
int mid = (l + r) / 2;
return query(cur * 2, l, mid, ql, qr) + query(cur * 2 + 1, mid, r, ql, qr) \
+ (min(qr, r) - max(ql, l)) * lazy[cur];
}給你一堆矩形,找出他們覆蓋範圍的總面積
\(n \leq 10^5, 矩形範圍 \leq 10^6\)
稀疏表
Sparse Table
問題又來了!
給你一個序列,每次詢問一個區間,輸出區間內數字的最小值(無修改)
\(n \leq 10^5, q \leq 2 * 10^6\)
用線段樹做?\(O((n + q)logn)\)
介紹倍增表><
令 \(sp[i][j]\) 為區間 \([j, j + 2^i - 1]的最小值\)
| 2 | 3 | 4 | 2 | 3 | 6 | 1 | 3 |
|---|
| 2 | 3 | 2 | 2 | 3 | 1 | 1 | x |
|---|
| 2 | 2 | 2 | 1 | 1 | x | x | x |
|---|
| 1 | x | x | x | x | x | x | x |
|---|
倍增表建立的方法
-
從小的\(i\)開始做,\(i = 0\)時,\(sp[i][j] = a[j]\)
-
對於 \([j, j + 2^i - 1]\)的最小值,可以將它拆成$$min([j, j + 2^{i - 1} - 1], [j + 2^{i - 1}, j + 2^i - 1])$$
-
記得 \(j\) 只能跑到 \(n - 2^i\)
#include <iostream>
#include <algorithm>
#define maxn 100005
using namespace std;
int sp[18][maxn], a[maxn];
int n;
int main() {
for (int i = 0;i < 18;i++) {
for (int j = 0;j < n - (1<<i) + 1;j++) {
if (i == 0) sp[i][j] = a[j];
else sp[i][j] = min(sp[i - 1][j], \
sp[i - 1][j + (1<<(i - 1))]);
}
}
}那這樣怎麼求區間最小?
Sparse Table 最強的是在當支援的函式
\(f\) 可以有\(f(i, i) = f(i)\)。
| 1 | 2 | 4 | 2 | 5 | 3 | 7 | 2 |
|---|
選定一個\(x\),使得兩個區間聯集會是整個區間