基本組合
aka 數(ㄕㄨˇ)數(ㄕㄨˋ)課
建國中學 賴昭勳
什麼是組合數學?
組合數學 (Combinatorics)
「組合數學是一門研究可數或離散對象的科學。」 -Wikipedia
離散: 非連續,可數的 (ex. 圖論)
不是離散的數學 (ex. 實數)
簡單來說,就是研究如何數能一個一個數的東西。
為什麼要學?
- 競程大部分的東西都是離散的
- 一半以上的「數學」題都會用到
- 可以會數數
符號
\(\sum\) : 求和符號 (Sigma)
\(\Pi\) : 求積符號 (Product)
\(\cap\) : 集合的交集
\(\cup\) : 集合的聯集
\(|A|\) : 集合\(A\)的大小
基本計數原則
加法原理
假設有 \(k\)個集合 \(A_1, A_2, ..., A_k\),任兩個集合皆互斥,則
\[|\cup_{i=1}^k A_i | = \sum_{i=1}^k |A_i|\]
當你要數符合某個條件的東西時,可以試著把它分成一些互斥的情況,把每種情況的方法數加起來得到答案。
乘法原理
假設有 \(k\)個集合 \(A_1, A_2, ..., A_k\),定義他們的笛卡爾積(Cartesian Product) 為集合
則
也就是說,假設每個集合都有\(c_i\)個東西可以選,那從每個集合各選一個東西有\(\Pi c_i\)種選法
來看例題吧
請問 2940 有幾個因數?
答:
36個
對於任意正整數\(n\),假設他的質因數分解為
\(n = \Pi p_i^{m_i}\)
則\(n\)有\(\Pi (m_i + 1)\)個因數
認識階乘
\(n\) 個相異的東西排成一列,有多少種方法?
第一個東西有\(n\)個位置可以選,第二個東西有\(n-1\)個位置,第\(i\)個東西有\(n-i+1\)個位置...
\(n\) 個相異的東西排成一列,有多少種方法?
答: \(n!\)
總共 \(n * (n-1) * ... * 1 = \Pi_{i=1}^n i \) 種
定義這個數字為 \(n! = \Pi_{i=1}^n i\)
額外定義 \(0! = 1\)
簡單例題
有\(n > 2\)個人(編號\(1, 2, ..., n\))圍著一桌圓桌坐,若\(1\)和\(n\)兩個人不相鄰,且兩種坐法若旋轉後一樣則視為同一種,那有多少種方法?
\(Ans: (n-1)! - 2(n-2)!\)
排列數 \(P_k^n\)
把剛剛的問題再延伸...
\(n\) 個相異的東西,選\(k\)個排成一列,有多少種方法?
用同樣的邏輯,第一個東西有\(n\)個位置可以選,第二個東西有\(n-1\)個位置,第\(k\)個東西有\(n-k+1\)個位置...
\(n\) 個相異的東西,選\(k\)個排成一列,有多少種方法? 答: \(P_k^n\)
定義 \(P_k^n = n * (n - 1) * ... * (n-k+1) = \frac{n!}{n-k!} \)
由此可以注意到,\(P_n^n = \frac{n!}{0!} = n!\)
與前面\(0! = 1\)的定義相符
重複排列問題
有\(n\)顆球被塗成\(k\)個不同顏色,其中塗成第\(i\)個顏色的有\(c_i\)顆球,將這\(n\)顆球排成一列有幾種方法? (同樣顏色的球視為同一種)
假設每個球都不一樣,那有\(n!\)種方法。
重複排列問題
考慮一種排法: RGGBRRB
對於每一種排法,把顏色相同的球再任意順序編號,則可以對應到\(\Pi c_i!\)種排列。
那麼方法數為 種。
再看一題
有\(n\)個男生和\(m\)個女生 (\(n \geq m\)) 要排成一列,有多少種排法使得任兩個女生不相鄰?
\(Ans: n!P_m^{n+1}\)
組合數 \(\binom{n}{k}\)
新的問題
從大小為\(n\)的集合中選出大小為\(m\)的子集有多少種選法?
Hint: 先排成一列,再處理順序問題
考慮順序的話,那有 \(P_m^n\) 種選法。
每個集合都有\(m!\)種排法。
從大小為\(n\)的集合中選出大小為\(m\)的子集有多少種選法? \(Ans: \binom{n}{m} \)
定義 \[C_m^n = \binom{n}{m} = P_m^n / m! = \frac{n!}{m!(n-m)!}\]
註: 先假設 \(n, m\)為非負整數且\(m \leq n\)
若\(m>n\)則定義\(\binom{n}{m} = 0\)
重複排列問題 (Part 2?)
有\(a+b\)顆球,\(a\)顆紅色\(b\)顆藍色排成一列,有多少種方法?
\(Ans: \binom{a+b}{a} = \binom{a+b}{b}\)
走格子問題
A
B
A到B,只往右或往下走有幾種走法?
卡特蘭數
一路領先問題: 求有多少個長度為\(2n\)的01字串,有\(n\)個\(0\)和\(n\)個\(1\),並且對於任意前綴,\(0\)的個數都比\(1\)多。
ex. 001011, 010011 為 \(n=3\)的合法字串
二項式定理與應用
組合數的規律
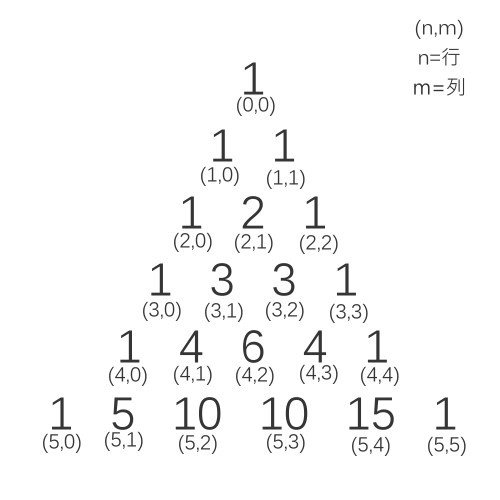
把各\(\binom{n}{m}\)的值寫成一個表格...
| n\m | 0 | 1 | 2 | 3 | 4 |
| 0 | 1 | ||||
| 1 | 1 | 1 | |||
| 2 | 1 | 2 | 1 | ||
| 3 | 1 | 3 | 3 | 1 | |
| 4 | 1 | 4 | 6 | 4 | 1 |
有什麼樣的規律?
組合恆等式
\(\binom{n}{m} = \binom{n-1}{m} + \binom{n-1}{m-1}\)
組合(Combinatorial) 證明: 從\(n\)個相異物品選出\(m\)個,如果選\(1\)號物品,剩下有\(\binom{n-1}{m-1}\)種方法;
不選的話,剩下有\(\binom{n-1}{m}\)種。
上一頁的表格又稱為巴斯卡三角形
二項式定理
若\(n\)為非負整數,\((x + y)^n\)的展開式為
\(x^n + \binom{n}{1}x^{n-1}y + ... + \binom{n}{1}xy^{n-1} + y^n \\ = \sum_{i=0}^n \binom{n}{i} x^iy^{n-i}\)
各係數可由巴斯卡三角形第\(n\)行求出
注意到,這代表巴斯卡三角形第\(n\)行的數字和,也就是 \(\sum_{i=0}^n \binom{n}{i} = 2^n\)
酷酷定理
Hockey Stick Identity:
\(\sum_{i=0}^m \binom{n+i}{i} = \sum_{i=0}^m \binom{n+i}{n} = \binom{n+m+1}{m}\)
Vandermonde's Identity (證明?)
\(\sum_{i=0}^n \binom{n}{i}\binom{m}{k-i} = \binom{n+m}{k}\)
小練習
有一個大小為\(n\)的集合\(A\),證明\(A\)每一個子集合的子集合總數為\(3^n\)。
給定\(x\),請輸出一個合法的巴斯卡路徑使其數字總和為\(x\)。
一個巴斯卡路徑由起點\((0, 0)\)開始,沿途經過相鄰格子(必須在三角形內),且同一格子最多經過一遍。格子\((i, j)\)上面的數字為\(\binom{i}{j}\)
排容原理
回顧加法原理
假設有 \(k\)個集合 \(A_1, A_2, ..., A_k\),任兩個集合皆互斥,則
\[|\cup_{i=1}^k A_i | = \sum_{i=1}^k |A_i|\]
那麼兩個集合不互斥怎麼辦?
需要想辦法扣掉多餘的情況...
簡單一點的情況
只有三個集合
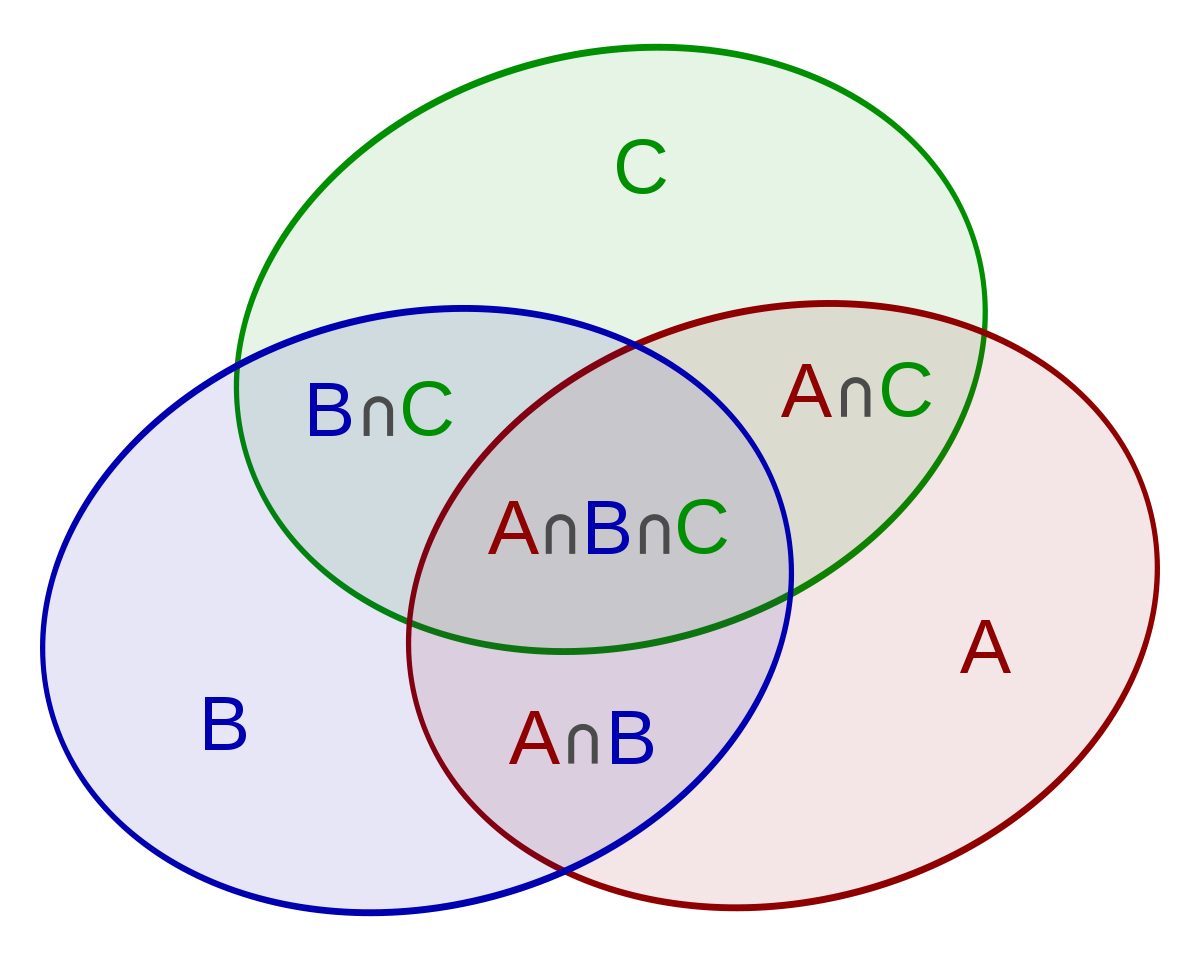
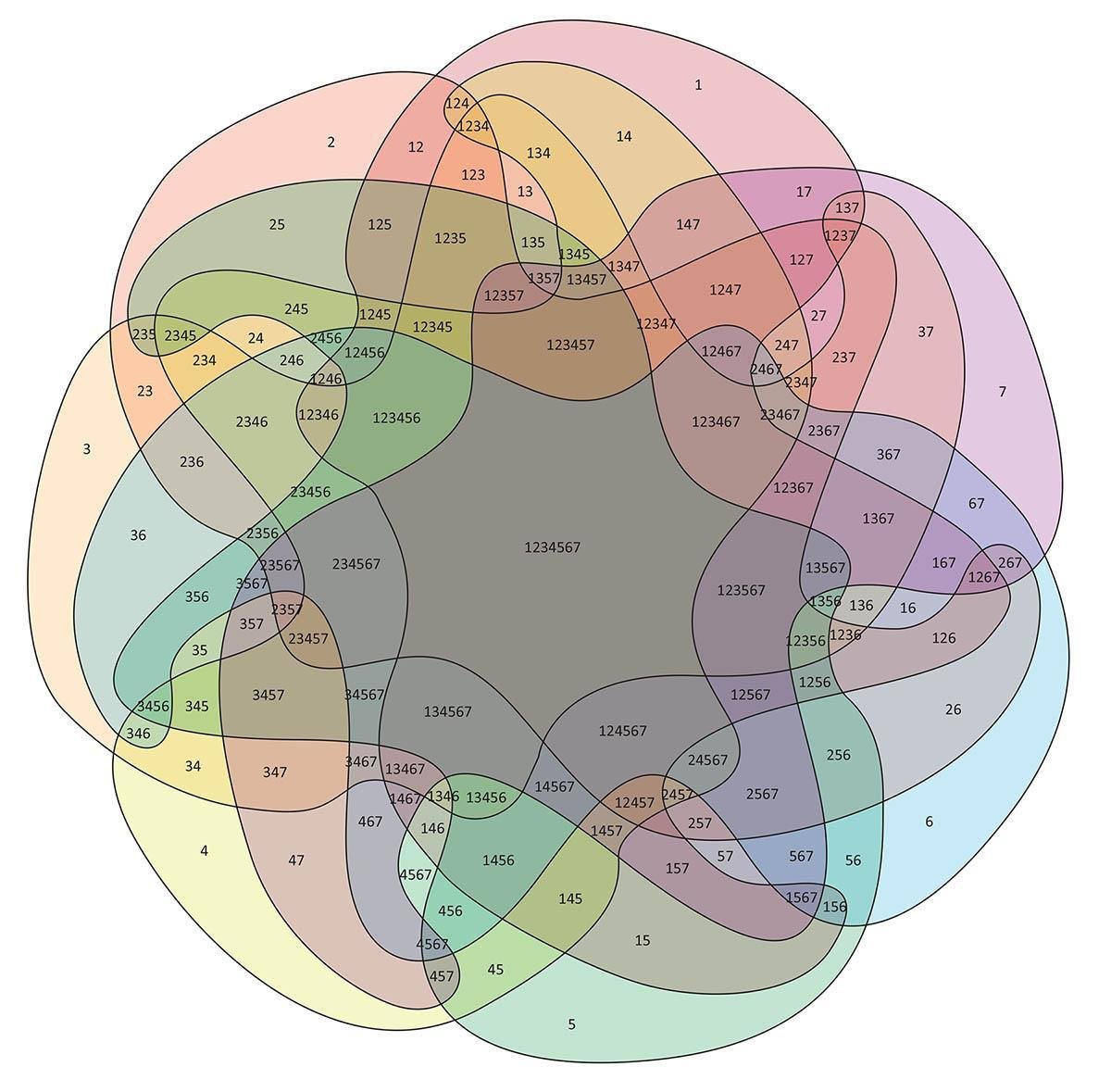
一般化?
排容原理
假設有 \(k\)個集合 \(A_1, A_2, ..., A_k\),則
\[|\cup_{i=1}^k A_i | = \sum_{i=1}^k (-1)^{i+1} \sum_{p_1 < p_2 < ... < p_i} |A_{p_1} \cap A_{p_2} \cap ... \cap A_{p_i}|\]
錯排問題
歐拉\(\phi\)函數
想不到吧
第二類斯特林數 \(S(n, m)\)
排容原理的精神
把多的東西扣掉
把多扣的東西加回來
把多加的東西扣掉
...