AI初體驗:挑戰2048
建國高中 1年23班 賴昭勳
前言
在2014年,一個簡單的網頁小遊戲(2048)在網路上爆紅。
基本的規則為:在4x4的方格上散佈著數字方塊,依照鍵盤移動至方形的四邊,兩塊數字相同的方塊遇到時就會相加且合併,無法移動時遊戲結束。玩家需嘗試由2和4的方塊經過上述過程組成數字2048。
對此遊戲深感好奇的我,開始思考著有沒有可能用電腦算出最佳的步驟?而完美的「2048 人工智慧」是否存在?
Step 1: 架設背景環境
-
模擬真正的2048遊戲
-
有方便觀察的介面
Step 1-1 在本機做出2048
-將盤面狀態存成一個4*4的二維矩陣 (board.b)
-定義移動運算。將四種移動(上、下、左、右)存放為「檢查索引格的移動方向」的資料(x, y):左 (1, 0)、 右(-1, 0)、上(0, -1)、下(0, 1)。
def move(self, x, y, obj, *args, **kwargs):
global score
# left=(1, 0), right=(-1, 0), up=(0, 1), down=(0, -1)
if (x, y == 1, 0 or x, y == 0, 1):
self.c = [0, 0]
ind = 0
if (x == -1 and y == 0):
self.c = [3, 0]
ind = 3
if (x == 0 and y == -1):
self.c = [0, 3]
ind = 3
for i in range(4):
if x > 0 or y > 0:
ind = 0
else:
ind = 3
for j in range(4):
if x != 0:
cpos = obj[i][self.c[0] + x * j]
if cpos != 0:
if self.c[0] + x * j != ind:
obj[i][self.c[0] + x * j] = 0
if cpos == obj[i][ind] and self.c[0] + x * j != ind:
obj[i][ind] *= 2
countscore = kwargs.get('countscore', None)
if countscore != False:
score += obj[i][ind]
obj[i][self.c[0] + x * j] = 0
ind += x
elif cpos != obj[i][ind] and obj[i][ind] != 0:
ind += x
obj[i][ind] = cpos
else:
obj[i][ind] = cpos
elif y != 0:
cpos = obj[self.c[1] + y * j][i]
if cpos != 0:
if self.c[1] + y * j != ind:
obj[self.c[1] + y * j][i] = 0
if cpos == obj[ind][i] and self.c[1] + y * j != ind: # combine
obj[ind][i] *= 2
countscore = kwargs.get('countscore', None)
if countscore != False:
score += obj[ind][i]
obj[self.c[1] + y * j][i] = 0
ind += y
elif cpos != obj[ind][i] and obj[ind][i] != 0: # move to numbered block
ind += y
obj[ind][i] = cpos
else:
obj[ind][i] = cposStep 1-2 接到螢幕上!

使用pygame模組,以2048遊戲板為背景,一個個把board.b的物件blit在螢幕上。
for i in range (17):
numbers.append(pygame.transform.scale(pygame.image.load("assets/" + str(2 ** (i + 1)) + ".png"), (90, 90)))
while (running) {
display = GameEngine.game.b
for i in range(4):
for j in range(4):
if display[i][j] != 0:
try:
screen.blit(numbers[int(math.log(display[i][j], 2)) - 1], (215 + 105*j, 215 +105*i))
except ValueError:
pass
pygame.display.update()
}問題:
一次怎麼同時跑好幾段程式?
A:使用Threading 模組
import threading
engine = threading.Thread(target=GameEngine.run)
engine.daemon = True
engine.start()紀錄遊戲的工具
利用檔案讀寫,以時間為檔名
第一行為每一步的動作(wasd)
第二行為隨機產生方塊的位置與類型
(a~p, A~P)
第三行為總分
Step 2: AI的雛形
-
做出可以自行判斷的機器
-
建立計算的架構
目標:從一個遊戲狀態中推導出下一個最好的步驟

2-1 初版設計
先讓他隨機跑很多次,看哪一個分數最高
Step 2-2:判斷高分條件


Step 2-2:判斷高分條件


Step 2-2:判斷高分條件

Step 2-2:判斷高分條件
剩下空格數多寡
大的方塊在角落
大小相近的方塊在附近
其他的東西 (?)
價值函數(Value Function)
越高越好
Step 2-3:搜尋之後的狀態
- 2048有隨機產生因素,也要把所有可能的方塊考慮進去嗎?
- 如果要的話,複雜度肯定爆?
使用深度優先搜尋(DFS),並指定一個預設深度
Expectimax 演算法
有點像minimax, 但是對手的動作是有機率權重的
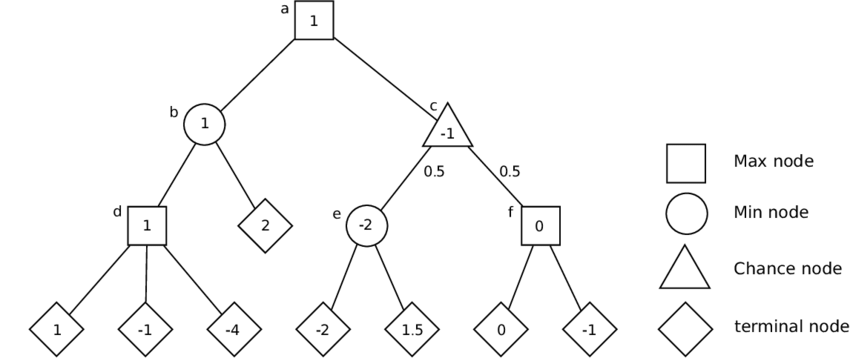
Expectimax 是啥?能剪枝嗎?
因為必須考慮到對方動作之後價值函數的期望值,所以沒有剪枝方法!
2048 的 Expectimax 實作
def best_move(test, depth, isGameState):
global output, checkdepth, boardval
if depth >= checkdepth:
return val(test)
if isGameState: #Player's Turn
save = list(test[i].copy() for i in range(4))
best = -1000.0
bm = ()
for p in possible_moves(test):
test = list(save[i].copy() for i in range(4))
GameEngine.board.move(GameEngine.board, p[0], p[1], test, countscore=False)
###
v = best_move(test, depth + 1, False)
###
best = max(best, v)
if best > v and depth == 0:
bm = p
if depth == 0:
output = movetostr(bm)
return best
else: #Adding new tile
total = 0.0
fours = 0.0
moves = 0
for o in empty_pieces_list(test):
newboard = list(test[i].copy() for i in range(4))
addpos(newboard, o, 2)
###
v = best_move(newboard, depth + 1, True)
###
total += v
newboard = list(test[i].copy() for i in range(4))
addpos (newboard, o, 4)
v = best_move(newboard, depth + 3, True)
fours += v / 9
moves += 1
if moves == 0:
return 0
return total / moves + fours / moves目前成果
最多到1024/512, 到不了2048,而且常常在256的時候就掛了qq
Step 3: 效率優化
-
加速計算
-
做更多計算
Step 3-1: 動態改變搜尋深度
因為空著很多塊的時候,隨機層會出現一堆可能,但是空著越多塊,活下去的難度其實越低


Step 3-1: 動態改變搜尋深度
很多步其實是重複算到
(而且Expectimax好像深度不用那麼深)
if depth == 0:
if checkdepth <= 3 or len(empty_pieces_list(test)) < 3:
checkdepth = min(8, int(2 * int(math.sqrt(16 - sum(empty_pieces(test[i]) for i in range(4))))))
else:
checkdepth -= 2Step 3-2: 改變移動規則...
原本是用一格一格慢慢動,要多跑一個while迴圈。
改成:
迭代每排的物件,把所有格子加到list上面,然後再貼回去。
| 遊戲開始時跑depth=7的搜尋一步: | 時間 |
|---|---|
| 原本 | 11.2秒 |
| 改良後 | 2.6秒 |
Step 3-3: 減少重複搜尋
2048的Expectimax其實是可以更快的! 因為會有重複的遊戲狀態。可以用dfs先找到某狀態的價值分數,存起來,之後重複就直接用。
那要怎麼儲存遊戲狀態?
Step 3-3: 減少重複搜尋
Python 的字典 (Dictionary):
-有key(索引值)和value(對應值)
-好像跟c++的map一樣?
其實2048裡的每一個數字都可以寫成
所以只要把x記下來就好(然後空白時令x=0)。
x不太會超過16
Step 3-3: 用bitset存
變成一個64bit二進位數字 (long long?!)
def bitset(obj):
output = 1
for i in range(16):
if obj[i // 4][i % 4] != 0:
output += pow(16, i) * math.log2(obj[i // 4][i % 4])
return output
def best_move(test, depth, isGameState):
global output, checkdepth, boardval
if depth == 0:
boardval = dict()
#略
if isGameState:
#略
for p in possible_moves(test):
tempbm = p
test = list(save[i].copy() for i in range(4))
GameEngine.board.move(GameEngine.board, p[0], p[1], test, countscore=False)
s = best
if bitset(test) not in boardval:
v = best_move(test, depth + 1, False)
boardval[bitset(test)] = v
else:
v = boardval[bitset(test)]
best = max(best, v)
if s != best and depth == 0:
bm = p
#略
return best
else:
#略
return total / moves + fours / movesStep 4: 做出好一點的AI
-
一直改參數
-
做到快瘋了qq
Step 4-1:崩潰中...
經過數週的掙扎,實在想不到更好的辦法,只能到程式設計師最愛的網站找答案了...



Step 4-2:單調性
簡單來說,就是一排有沒有由小到大。


def dif_values(l):
#count = 0
mono = 1
for i in range(4):
monox, monoy = 0, 0
pmx, pmy = 0, 0
for j in range(3):
mx = math.log2(max(1, l[i][j + 1]) / max(1, l[i][j]))
my = math.log2(max(1, l[j + 1][i]) / max(1, l[j][i]))
#count += abs(mx) + abs(my)
monox += mx
pmx += abs(mx)
monoy += my
pmy += abs(my)
mono += ((pmx - abs(monox))**3 + (pmy - abs(monoy))**3)
return mono遇到的問題
只靠單調性到不了2048
因為他沒有合併應該合併的

Step 4-3:空格數
將分數乘以(空格數 + 0.5)
Step 4-4:鼓勵合併
定義門檻變數為最大方塊/8 (低三個階級)
比門檻大的方塊我們希望合併越多越好
找出現在的合併情形,與完美的情形
psum = 1
total = 0
penalty = maxpiece / 8
for x in range(4):
for y in range(4):
if test[y][x] >= min(16, penalty):
psum *= math.sqrt(math.log(test[y][x], 2))
total += test[y][x]
def LTM(a): # Least Tile Multiple
opt = 1
while a:
x = int(math.log2(a))
a -= 2**x
opt *= math.sqrt(x)
return opt
Step 4-5:想辦法結合各函數
沒什麼方法(吧?),就一直試。
return (total + total * LTM(total) / psum) * (tiles + 0.5) / math.sqrt(position_buff)
- position_buff: 單調性(數字越大越糟)
- tiles: 空格數
- psum: 合併函數
- total:重要方塊總和
- LTM(total): 最佳合併函數
Step 4-6:其他想法
目前最大的缺點有:
- 在最後會莫名其妙死
- Expectimax 個例影響結果?
- 只會靠某幾邊(DFS有問題?)
成果!
跑十場:
平均分數:13746.8
最高分:~26000
最少達到:512+256