演算法與排列組合

建國中學 賴昭勳

提問/回答的網站: slido

#68610

暖身大水題

從一個有6顆不同的球的袋子中任意取3顆球，有幾種取法？

今天的主題：動態規劃

(Dynamic Programming)

DP是什麼？

當一個問題可以被分成很多個問題合併起來的時候（遞迴關係），則可以將小問題的結果存起來，去往後推大問題的答案。

經典範例

求費氏數列的第n項

時間複雜度 O(n)

遞迴表示方法？

f(1) = 1, f(2) = 1

f(n) = f(n - 1) + f(n - 2)

直接寫遞迴

int fib(int n) {
	if (n == 1 || n == 2) return 1;
    else return fib(n - 1) + fib(n - 2);
}

感覺有點沒效率？

DP: 存取小問題的答案

int f[1000];
int fib(int n) {
	f[1] = f[2] = 1;
    for (int i = 3;i <= n;i++) {
    	f[i] = f[i - 1] + f[i - 2];
    }
    return f[n];
}

當問到的數字已經被算過了，就直接拿來用。

時間複雜度：線性 O(n)

這聽起來有點廢話...?

（也是很經典的）例題

有個 n=8 階的樓梯，每次可以往上走1, 2, 3階，共有幾種走完8階的方法？

可在slido 回答！

概念和費氏數列一樣！

dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

int dp[n + 1];
dp[0] = 0, dp[1] = 1, dp[2] = 2;
for (int i = 3;i <= n;i++) {
	dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}

DP 三要素

  1. 定義

  2. 狀態轉移方式

  3. 初始狀態（邊界條件）

小結論

DP 是一個解題手法。對於一個有遞迴關係的題目，先將小問題的答案存下來，再去解決大問題。

與排列組合的關聯

有一些題目，直接排組下去太難了！

例如：https://tioj.ck.tp.edu.tw/problems/1354​

題：有一隻青蛙在A, B, C, D四個石頭之間跳。青蛙從A開始，每次跳到不同的石頭，問跳n次之後停在A的方法有幾種？

ex. N = 5

DP 可以維護好幾種東西

  1. 定義：令 dp[i][0] 代表跳了 i 次之後，不在 A 的方法數，dp[i][1] 代表跳了 i 次回到A的方法。
  2. 轉移方式：dp[i][1] = dp[i - 1][0],                                    dp[i][0] = 3 * (dp[i - 1][1] + 2 * dp[i - 1][0])
  3. 初始條件：dp[0][1] = 1, dp[0][0] = 0

再一個例題

有 n=10 個排成一排的座位。

定義一種坐法是「尷尬」為：原本坐的人兩兩不相鄰，但是再加一個人就一定會出現相鄰的狀況。

有幾種「尷尬」的坐的方法？

思考的方向

考慮「增加一個位置時」可以出現哪些情況，因為這很可能是dp（遞迴）會用到的。

參考做法

  1. 定義：dp[i][0] 代表長度為 i 且最後一項是空的時候有幾種方法。dp[i][1] 代表長度為 i 且最後一項有坐人的方法數。

  2. 轉移：考慮以下情況。

 

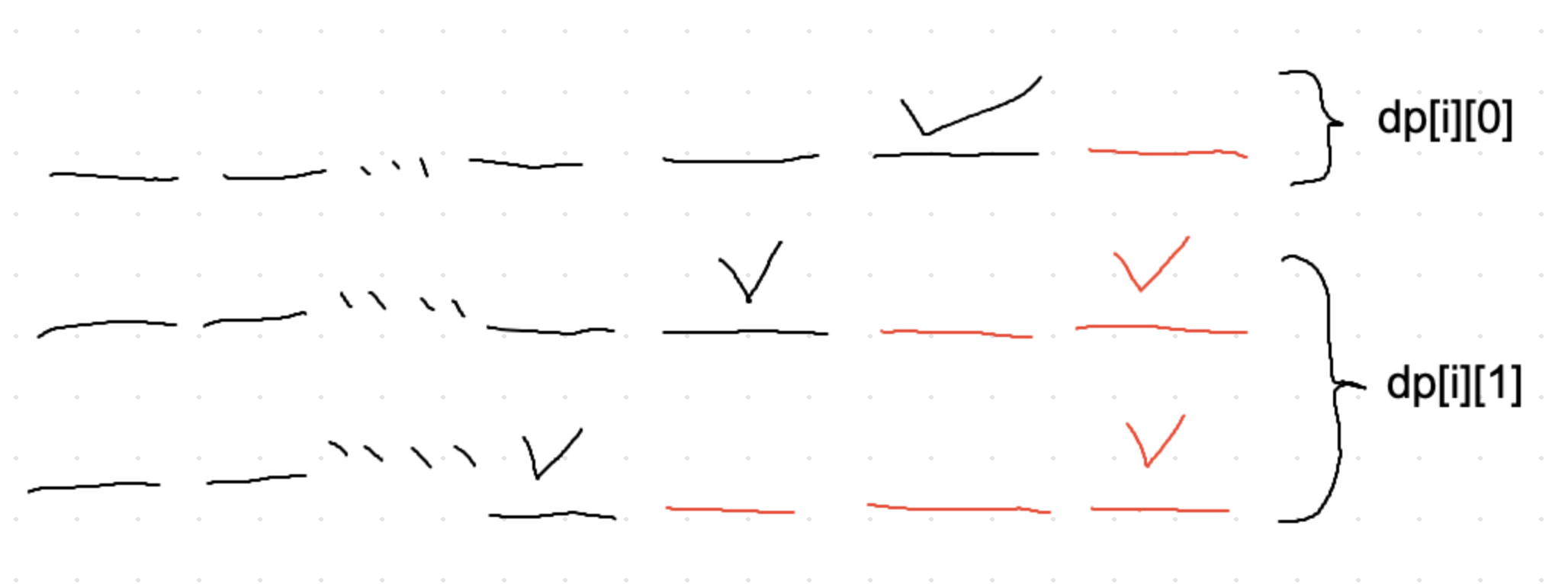
因此可以得到：

dp[i][0] = dp[i - 1][1]

dp[i][1] = dp[i - 2][1] + dp[i - 3][1]

參考做法

3. 打表，寫好初始條件

i =  1 2 3 4 5 6 7 8 9
dp[i][0] 0 1 1 1 2 2 3 4 5
dp[i][1] 1 1 1 2 2 3 4 5 7

答案：dp[n][0] + dp[n][1]!

其實，dp 不一定要是一維的。

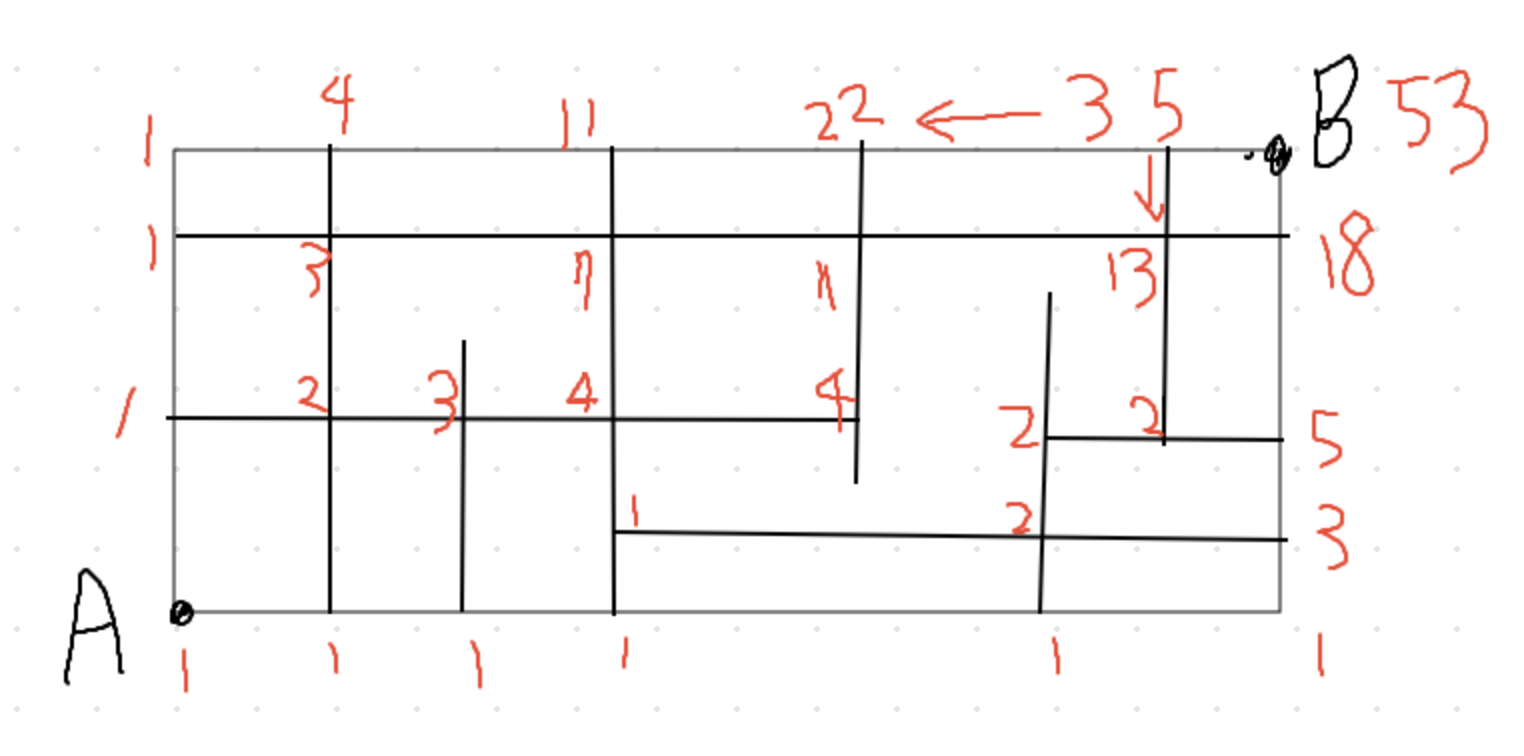
原來這也是dp

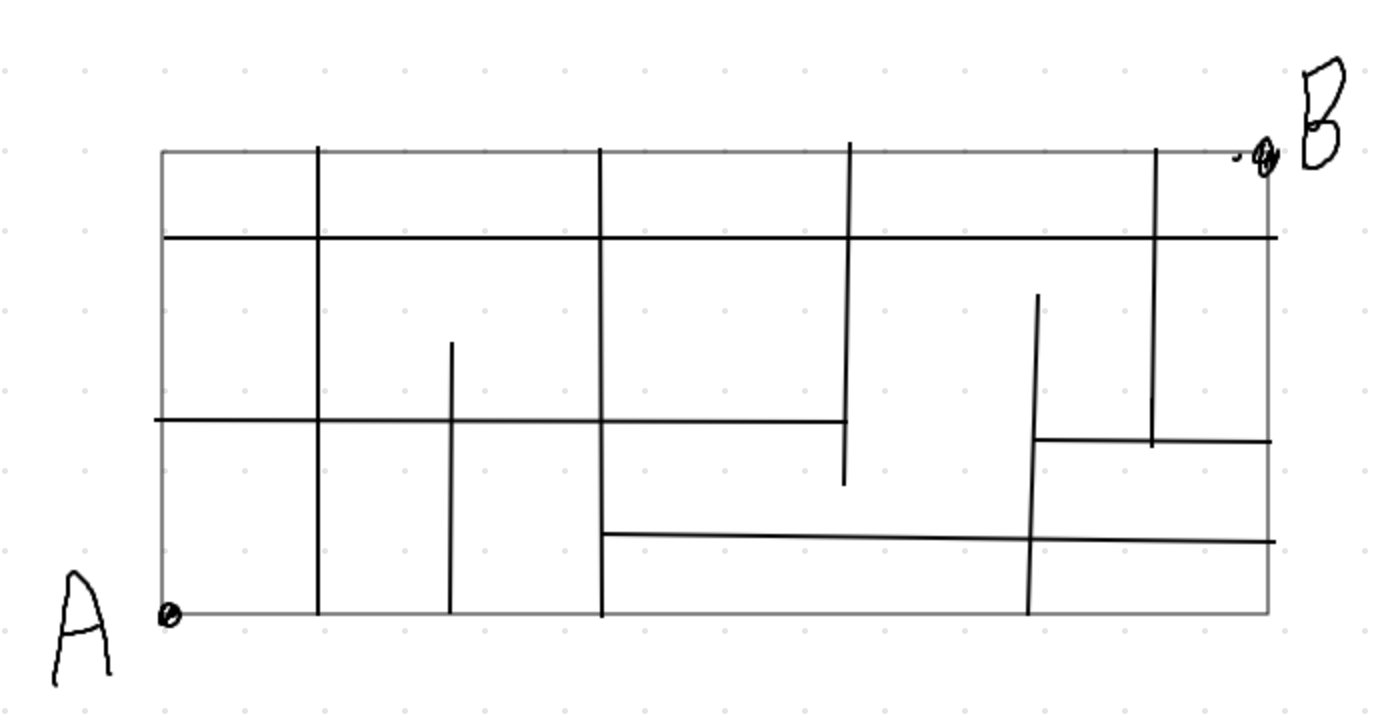
從A到B，只往右或往上，有幾種走法？

狀態轉移->把兩個路徑的方法數加起來

例題： https://tioj.ck.tp.edu.tw/problems/1291

將n個相同的箱子放入m顆不同的球，有幾種方法？ (n, m <= 200)

 

ex. n = 3, m = 5

把dp 的定義想的活一點

      dp[i][j] 代表，有n個箱子和m顆球，且每個箱子至少有一顆的方法數。

 

這樣子答案就會變成：

 

那轉移呢？

\Sigma_{i = 1}^{n} dp[i][m]

把dp 的定義想的活一點

若 j < i (球數小於箱子數），dp[i][j] = 0

否則，有兩種方法達到dp[i][j]:

從dp[i - 1][j - 1] 多一個箱子跟球，球在那個新的箱子裡。

從dp[i][j - 1] 中加一個球進去，有 i 個位置可以加。

 

因此：dp[i][j] = dp[i - 1][j - 1] + i * dp[i][j - 1]

i\j 1 2 3 4 5
1 1 1 1 1 1
2 0 1 3 7 15
3 0 0 1 6 25

最後一題！

https://tioj.ck.tp.edu.tw/problems/1296

有一個2xn 的表格，現在要將1~2n放進去，必須符合：左邊格子<右邊格子且

上面格子<下面格子。 有幾種方法？

 

 

 

 

ex: n = 4

 

註：這題討論的是O(n^2)的解

1 2 5
3 4 6
1 3 4
2 5 6
2 3 4
1 5 6

解決dp問題的重點

轉換問題！

假設我們已經知道一個橫排要選哪些數

(ex. 1 3 4 5), 那麼那些數只有一種排法！

此問題等價於：將1~2n的數字標示 n 個 A 和n 個B，代表那個數字要寫在上面還是下面。則有幾種作法讓任一前綴中 A的個數>=B的個數？

AAABBB, ABAABB (O)

AABBBB, ABBABB (X)

看似一維的題目也可以用二維dp

dp [i][j] 代表，長度為 i，

A的個數 - B的個數 = j 的方法數

這樣的話，答案就是 dp[n][0]

轉移：dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]

j\i 1 2 3 4 5 6 7 8
8 1
7 1
6 1 7
5 1 6
4 1 5 20
3 1 4 14
2 1 3 9 28
1 1 2 5 14
0 1 2 5 14

什麼時候該用？

可以有「遞迴」關係的問題！

一般的排列組合還是用正常方法寫吧！

所以DP到底在幹嘛？

聽起來只是一種遞迴的另一個稱呼...

DP 的應用

LIS, LCS, Edit Distance

無法Greedy的最佳解問題

Bitset DP 

單調隊列、四邊形優化、Aliens DP...

從很簡單到超級難的題目，

從APCS（第四題） 到 IOI，

DP無所不在。

更多DP跟排組的東西

  • 卡特蘭數

  • 錯排

  • 如何計算C(n, k)...

  • H(n, k)

 

謝謝各位的聆聽

Made with Slides.com