DFS
BFS
&
Motivation
There are several strategies to search for data or detect specific conditions.
We can organize our data in many ways. Sometimes the data structures can be complex tress or graphs.
We are going to talk about:
DFS and BFS
DFS(Depth First Search)
Involves searching a node and all its children before proceeding to its siblings.
1
2
3
4
BFS(Breadth First Search)
Involves searching a node and its siblings before going on to any children.
1
2
3
4
Examples
Examples
Amazing visualizations site:
Implementation
DFS
javascript (recursive)
function depthFirstSearch(nodeName, tree) {
if (tree.name === nodeName) {
return tree; //Node found
} else {
var children = tree.children;
if (children !== null) {
var result;
for (var i = 0; i < children.length; i++) {
result = depthFirstSearch(nodeName, children[i]);
if (result !== undefined) {
return result; //Return the node
}
}
}
}
}Implementation
DFS
javascript (iterative) uses a Stack
function depthFirstSearchIterative(nodeName, tree) {
var stack = new Stack(),
currentNode,
children,
found = false;
stack.push(new Node(tree));
while ((!stack.empty()) && (!found)) {
currentNode = stack.pop().value();
children = currentNode.children;
if (currentNode.name === nodeName) {
found = true;
} else if(children !== null) {
var childrenCount = children.length;
for (var i = childrenCount - 1; i >= 0; i--) {
stack.push(new Node(children[i]));
}
}
}
}Implementation
BFS
javascript (iterative) uses a Queue
function breadthFirstSearch(nodeName, tree) {
var queue = new Queue(),
currentNode,
children,
found = false;
queue.add(new Node(tree));
while (!queue.empty()) {
currentNode = queue.remove().value();
if (currentNode.name === nodeName) { //Node found
found = true;
return currentNode;
} else {
children = currentNode.children;
if (children !== null) {
for (var i = 0; i < children.length; i++) {
queue.add(new Node(children[i]));
}
}
}
}
}Time complexity
DFS
O (V+E)
Time Complexity of DFS is not O(V+E). Actually it depends on the data structure you are using to represent your graph. If you represent your graph using adjacency list then only it will be O(V+E).
BFS
So for V number of vertices time complexity becomes O(V*N) = O(E) , where E is the total number of edges in the graph. Since removing and adding a vertex from/to Queue is O(1) , why it is added to the overalltime complexity of BFS as O(V+E)
Space
BFS consume much more space than DFS because it requires to store all the child pointers at every level.
Uses
DFS
- Is there a path from A to B
- Is an undirected graph conected
- Is a directed graph strongly connected (if every vertex is reachable from every other vertex)
- To output the contents (e.g., the vertices) of a graph
- To find the connected components of a graph
- To find out if a graph contains cycles and report cycles.
Uses
BFS
- Is there a path from A to B
- What is the shortest path from node A to node B in and unweighted graph (for weighted graph we use Dijkstra's Algorithm)
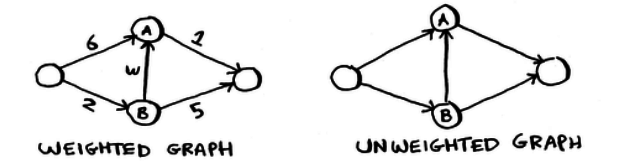
What can BFS do and DFS can’t?
- Finding shortest paths (in unweighted graphs)
if we have a very large tree and want to be prepared to quit when we get too far from the original node, DFS can be problematic; we might search thousands of ancestors of the node, but never even search all of the node's children. In these cases, BFS is typically preferred.
What can DFS do and BFS can’t?
- Finding out if a connected undirected graph is biconnected ( if there are no vertices whose removal disconnects the rest of the graph)
- Application in computer networks: ensuring that a network is still connected when a router/link fails.
Not biconnected
Extra example
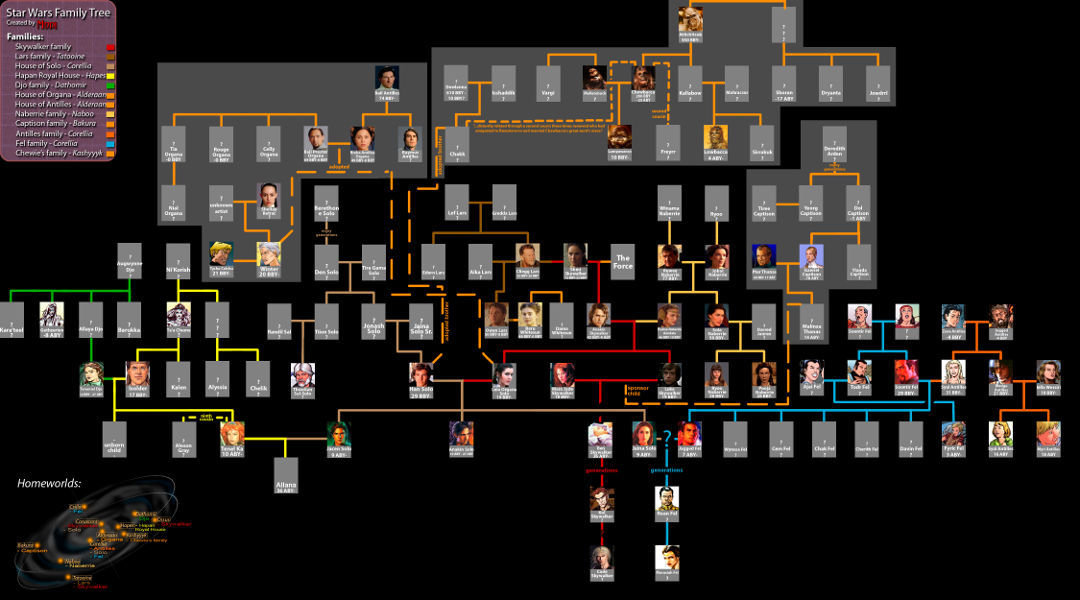
Given a family tree if one were looking for someone on the tree who’s still alive, then it would be safe to assume that person would be on the bottom of the tree.
- BFS would take a very long time to reach that last level
- DFS, however, would find the goal faster
However, if one were looking for a family member who died a very long time ago, then that person would be closer to the top of the tree.
- BFS would be better