Stacks

Definition

Abstract *linear data structure represented by a real physical stack or pile

(*) only one element can be reached directly

LIFO

(last in first out)

Basic Operations

Top

Time Complexity

Push	O ( 1 )
Pop	O ( 1 )
Top	O ( 1 )
Search	O ( n )

Implementation

class Node(object):
    def __init__(self, value):
        self.next = None
        self.data = value

class Stack:
    def __init__(self):
        self.top = None

    def pop(self):
        if (self.top):
            temp_data = self.top.data
            self.top = self.top.next
            return temp_data;

    def push(self, value):
        new_node = Node(value)
        new_node.next = self.top
        self.top = new_node

Linked list

Uses

Undo / Redo operations
Expression evaluation and syntax parsing
Backtracking
Call stack

Call Stack

If we call:

def greet(name):
    print "hi!"
    whatsup(name)
    print "getting ready to say bye..."
    bye()

def whatsup(name):
    print "whatsup, " + name + "?"

def bye():
    print "ok bye!"

greet("Triceracop")

def greet(name):
    print "hi!"
    whatsup(name)
    print "getting ready to say bye..."
    bye()

def whatsup(name):
    print "whatsup, " + name + "?"

def bye():
    print "ok bye!"

name:	"Triceracop"

If we call:

greet("Triceracop")

greet

name:	"Triceracop"

Print "hi!"

greet

name:	"Triceracop"

whatsup

name:	"Triceracop"

Print "whatsup Triceracop?"

greet

name:	"Triceracop"

greet

name:	"Triceracop"

bye

Print "ok bye!"

greet

name:	"Triceracop"

name:	"Triceracop"

Be aware of recursion

There is a cost: saving all that info can take up a lot of memory. Each of those function calls take up some memory, and when your stack is too tall, that means your computer is saving information for a lot of function calls.

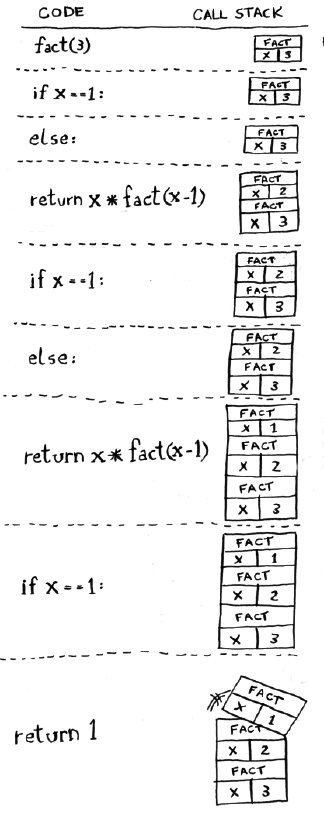
def fact(x):
if x == 1:
return 1
else:
return x * fact(x-1)

name:	"Triceracop"

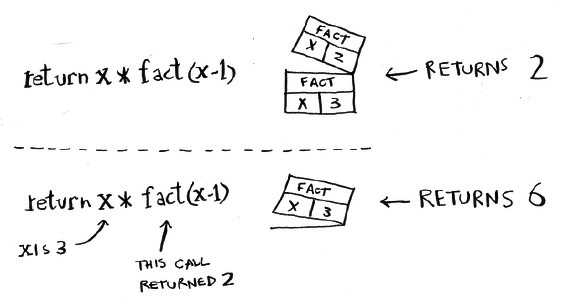
Be aware of recursion

Exercises

Describe how you could use a single array to implement three stacks

Exercises

How would you design a stack which, in addition to push and pop, also has a function min which returns the minimum element? Push, pop and min should all operate in O(1) time

Exercises

Implement a MyQueue class which implements a queue using two stacks

class MyQueue:
    def __init__(self):
        self.stackNewest = Stack()
        self.stackOldest = Stack()

    def add(value):
      self.stackNewest(value)

    def shiftStacks():
      if (stackOldest.isEmpty()):
        while !self.stackNewest.isEmpty():
          self.stackOldest.push(stackNewest.pop())

    def peek():
      self.shiftStacks()
      return self.stackOldest.peek()

    def remove():
      self.shiftStacks()
      return self.stackOldest.pop()

Exercises

In the classic problem of the Towers of Hanoi, you have 3 rods and N disks of different sizes which can slide onto any tower. The puzzle starts with disks sorted in ascending order of size from top to bottom (e.g., each disk sits on top of an even larger one). You have the following constraints:

(A) Only one disk can be moved at a time.
(B) A disk is slid off the top of one rod onto the next rod.
(C) A disk can only be placed on top of a larger disk.
Write a program to move the disks from the first rod to the last using Stacks.

http://haubergs.com/hanoi

http://www.softschools.com/games/logic_games/tower_of_hanoi/

THANKS

References

Grokking algorithms
Cracking the coding interview