Bijective Rotations on Hexagonal Lattice

by K. Pluta, T. Roussillon, D. Cœurjolly,

P. Romon, Y. Kenmochi, V. Ostromoukhov

Image from page 339 of "The natural history of British insects"

21/06/2018, JIG 2018, Lyon

Motivations

Digitized rotations on the square grid are burdened with an incompatibility between rotations and the geometry of the grid.

Agenda

Introduction to the Bees' Point of View
Quick Introduction to Rigid Motions
Bijective Digitized Rotations
Contributions
Conclusions & Perspectives

The beehive figure's source and author unknown (if you recognize it, please let me know). The image of the bee comes from http://karenswhimsy.com/public-domain-images (public domain)

Contributions in Short

Characterization of bijective digitized rotations on the regular hexagonal lattice
Comparison of frequencies of such rotations on the square and the regular hexagonal lattices

Pure, extracted honey

Related Studies

Pluta, K., Romon, P., Kenmochi, Y., Passat, N.: Bijective Digitized Rigid Motions on Subsets of the Plane. Journal of Mathematical Imaging and Vision (2017)
Pluta, K., Romon, P., Kenmochi, Y., Passat, N.: Bijectivity Certification of 3D Digitized Rotations. CTIC (2016)
Roussillon, T., Cœurjolly, D.: Characterization of Bijective Discretized Rotations by Gaussian Integers. Research report, LIRIS UMR CNRS 5205 (2016). URL: https://hal.archives-ouvertes.fr/hal-01259826

Introduction to the Bees' Point of View

The figure comes from http://thegraphicsfairy.com/vintage-clip-art-bees-with-honeycomb

The Lattices

\mathbb{Z}[\omega] = \mathbb{Z} \oplus \mathbb{Z}\omega, \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i

\mathbb{Z}[i] = \mathbb{Z} \oplus \mathbb{Z}i

Eisenstein:

and Gaussian:

integers

Properties

Property	Gaussian integers	Eisenstein integers
conjugate
squared modulus
units

\bar{\mathbf{x}} = a - b i

\bar{\mathbf{x}} = (a - b) - b \omega

| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 + b^2

| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 - a b + b^2

\Upsilon = \{ \pm 1, \pm i \}

\Upsilon = \{ \pm 1, \pm \omega, \pm \bar{\omega} \}

divisibility

\mathbf{y} | \mathbf{x} \text{ if } \exists \mathbf{z} \in \mathbb{Z}[\varkappa] \text{ such that } \mathbf{x} = \mathbf{y} \cdot \mathbf{z} \text{ and } \mathbf{y} \in \mathbb{Z}[\varkappa]

greatest common divisor

\gcd(\mathbf{x}, \mathbf{y}) = \mathbf{z} \in \mathbb{Z}[\varkappa]\text{ is defined as a largest }

\mathbf{z} \in \mathbb{Z}[\varkappa]\text{ (up to multiplications by units) which }

\text{divides both } \mathbf{x}\text{ and }\mathbf{y}

\text{Giving } a, b \in \mathbb{Z}\text{ and }\mathbf{x},\mathbf{y}, \in \mathbb{Z}[\varkappa], \varkappa \in \{i, \omega\}

Digitization Model

A hexagonal cell of

\kappa

denoted by

\mathcal{C}_{\zeta}(\kappa),

\kappa\in \mathbb{Z}[\omega], \zeta \in \mathbb{C}.

\kappa

Digitization Model

The digitization operator is defined as

\mathcal{D}: \mathbb{C} \rightarrow \mathbb{Z}[\omega]

such that

\forall \mathbf{x} \in \mathbb{C}, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}[\omega]

\mathbf{x} \in \mathcal{C}_1(\mathcal{D}(\mathbf{x})).

and

\mathcal{D}(\mathbf{x})

Quick Lesson on Rigid Motions

Or how to become a beekeeper. Part I - Equipment

The figure comes from Wikimedia. Original source The New Student's Reference Work (public domain)

\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{C} & \to & \mathbb{C} \\ & & \mathbf{x} & \mapsto & \mathbf{a} \cdot \mathbf{x} \end{array} \right.

Rotations on

\mathbb{C}

Properties

Do preserve distances
Bijective

\mathbf{a}

– a unit modulus complex number

\theta = \arg(\mathbf{a})

– a rotation angle

U = \mathcal{D}\ \circ \mathcal{U}_{|\mathbb{Z}[\omega]}

\mathbb{Z}[\omega]

Properties

- Non-injective

- Non-surjective

- Do not preserve distances

\mathcal{U}(\mathbb{Z}[\omega])

Rigid Motions on

A digitized rotation is bijective if and only if

\forall \mathbf{p} \in \mathbb{Z}[\omega] \; \exists ! \mathbf{q} \in \mathbb{Z}[\omega]

such that

\mathcal{U}(\mathbf{q}) \in \mathcal{C}_1(\mathbf{p}).

\mathcal{U}

- a continuous rotation

\mathcal{C}_{\mathbf{a}}(\mathbf{p})

- a digitization cell centered at

\mathbf{p}

\mathbb{Z}[\omega]

- the hexagonal lattice

Conditions for Bijectivity

and multiplied by

\mathbf{a}

Bijective Digitized Rotations on Hexagonal Lattice

The figure comes from Wikimedia. The original source The honey bee: a manual of instruction in apiculture (public domain)

The figure of bumble bee comes from http://www.ase.org.uk (public domain), The bee figure by Pearson Scott Foresman, Wikimedia.

Set of Remainders

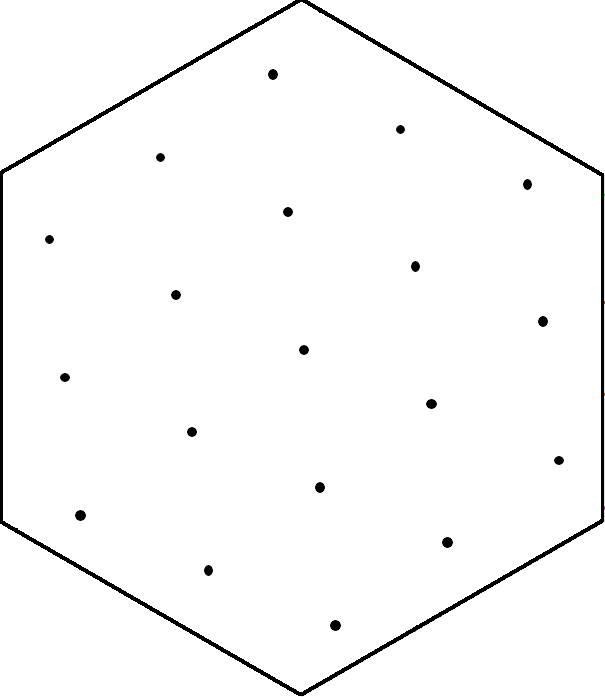
\forall \mathbf{p} \in \mathbb{Z}[\omega]\ \exists! \mathbf{q} \in \mathbb{Z}[\omega], S_{\mathbf{a}}(\mathbf{p},\mathbf{q}) \in \mathcal{C}_1(0)

A 2D digitized rotation is then bijective when

Double Surjectivity

The double surjectivity condition is then

provided that

S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_1(0) = S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(0).

Primitive Eisenstein Integers

s, t \in \mathbb{Z}

0 < s < t

and

t - s

not being divisible by 3.

a = s^2 + 2 s t, b = t^2 + 2 s t

and

c = s^2 + t^2 + s t,

such that

Set of Remainders

The double surjectivity condition is then

provided that

\check{S}_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\mathbf{a}}(0) = \check{S}_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{|\mathbf{a}|}(0).

Primitive Eisenstein Integers

A bunch of facts

Set of Remainders

The double surjectivity condition is then

provided that

Proving Bijectivity

For which s and t,

are in the green but not in the

black hexagonal cell?

Proving Bijectivity

From the equation of the line passing through the vertices of the green line-segment we obtain:

Proving Bijectivity

Then, we substitute t with s + e to arrive at

which are violated when s = 1 or when s > 1 and e = 1.

From the equation of the line passing through the vertices of the green line-segment we obtain:

Proving Bijectivity

At the end we have to check if

\bar{\gamma}+ \omega

\bar{\gamma}-1

are members

of the lattice that spans the values of

S'_{\mathbf{a}}.

Proving Bijectivity

Step 2: Check if for s = 1 or s > 1 and e = 1, the uncommon space of the hexagonal cells does not contain Eisenstein integers.

s = 1

s > 1, t = s + 1

Proving Bijectivity

The Square Grid

The Hexagonal Grid

Conclusion & Perspectives

Or extracting the pure, organic honey

The figure comes from Wikimedia. The original comes from A practical treatise on the hive and honey-bee (public domain)

Characterization of bijective digitized rotations on the regular hexagonal lattice
Comparison of frequencies of such rotations on the square and the regular hexagonal lattices

Conclusion

Perspectives

Investigate bijectivity of digitized rigid motions on finite subsets of Eisenstein integers.

Thank you for your attention and see you again!