Rigid Motions on Discrete Spaces

by Kacper Pluta

Image from page 252 of "Coloured illustrations of British birds, and their eggs" (1842) and Image from page 339 of "The natural history of British insects"

Show me a Rigid Motion

Solar System Animation: https://youtu.be/gvSUPFZp7Yo

\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{C} & \to & \mathbb{C} \\ & & \mathbf{x} & \mapsto & \mathbf{a} \cdot \mathbf{x} + \mathbf{t} \end{array} \right.
∣U:C→Cx↦a⋅x+t\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{C} & \to & \mathbb{C} \\ & & \mathbf{x} & \mapsto & \mathbf{a} \cdot \mathbf{x} + \mathbf{t} \end{array} \right.

Rigid Motions on

\mathbb{C}
C\mathbb{C}

Properties

  • Do preserve distances
  • Bijective
\mathbf{a}
a\mathbf{a}

- a unit modulus complex number

\mathbf{t}
t\mathbf{t}

- a complex number

\theta = \arg(\mathbf{a})
θ=arg⁡(a)\theta = \arg(\mathbf{a})

- a rotation angle

\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{R}^2 & \to & \mathbb{R}^2 \\ & & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t} \end{array} \right.
∣U:R2→R2x↦Rx+t\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{R}^2 & \to & \mathbb{R}^2 \\ & & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t} \end{array} \right.

Rigid Motions on

\mathbb{R}^2
R2\mathbb{R}^2
\mathbf{R}
R\mathbf{R}

- a rotation matrix

\mathbf{t}
t\mathbf{t}

- a translation vector

Properties

  • Isometry

  • Bijective

Show me a Discrete Object

Show me a Digitized Rigid Motion

U = \mathcal{D}\ \circ \mathcal{U}
U=D ∘UU = \mathcal{D}\ \circ \mathcal{U}

Properties

  • Non-injective
  • Non-surjective
  • Do not preserve distances
\mathcal{U}
U\mathcal{U}

Digitized Rigid Motions

where

\mathcal{D}
D\mathcal{D}

is a digitization operator

U = \mathcal{D}\ \circ \mathcal{U}
U=D ∘UU = \mathcal{D}\ \circ \mathcal{U}

Properties

  • Non-injective
  • Non-surjective
  • Do not preserve distances
\mathcal{U}
U\mathcal{U}

Digitized Rigid Motions

where

\mathcal{D}
D\mathcal{D}

is a digitization operator

Agenda

Part I: 2D Discrete Spaces

  • Introduction to 2D Regular Grids
  • Neighborhood Motion Maps
  • Digitized Rigid Motions on Square vs. Hexagonal Grids
  • Bijective Digitized Rotations on Square Grid

Part II: 3D Digital Space

  • Introduction to Cubic Grid
  • Quick Introduction to 3D Rigid Motions
  • Spatial Rotations and Quaternions
  • Bijectivity of 3D Digitized Rotations

Conclusion & Perspectives

Part I:

2D Discrete Spaces

Contributions in Short

  • A general framework to study digitized rigid motions
  • Comparison of the digitized rigid motions defined on the square and hexagonal grids
  • Characterization of bijective digitized:
    • rigid motions on the square grid
    • rotations on the hexagonal grid
  • Three algorithms to characterize if a digitized rigid motion is bijective when restricted to a finite set

I Am Going to Talk About

  • A general framework to study digitized rigid motions
  • Comparison of the digitized rigid motions defined on the square and hexagonal lattices
  • Characterization of bijective digitized rigid motions on the square grid

Introduction to 2D Regular Grids

Coloured illustrations of British birds, and their eggs (1842)

The Lattices

\mathbb{Z}[\omega] = \mathbb{Z} \oplus \mathbb{Z}\omega, \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i
Z[ω]=Z⊕Zω,ω=−12+32i\mathbb{Z}[\omega] = \mathbb{Z} \oplus \mathbb{Z}\omega, \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i

The grids are then denoted by

\mathcal{H}
H\mathcal{H}
\mathbb{Z}[i] = \mathbb{Z} \oplus \mathbb{Z}i
Z[i]=Z⊕Zi\mathbb{Z}[i] = \mathbb{Z} \oplus \mathbb{Z}i

Eisenstein:

and Gaussian:

integers

Properties

Property Gaussian integers Eisenstein integers
conjugate
squared modulus
units
\bar{\mathbf{x}} = a - b i
x¯=a−bi\bar{\mathbf{x}} = a - b i
\bar{\mathbf{x}} = (a - b) - b \omega
x¯=(a−b)−bω\bar{\mathbf{x}} = (a - b) - b \omega
| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 + b^2
∣x∣=x⋅x¯=a2+b2| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 + b^2
| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 - a b + b^2
∣x∣=x⋅x¯=a2−ab+b2| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 - a b + b^2
\Upsilon = \{ \pm 1, \pm i \}
Υ={±1,±i}\Upsilon = \{ \pm 1, \pm i \}
\Upsilon = \{ \pm 1, \pm \omega, \pm \bar{\omega} \}
Υ={±1,±ω,±ω¯}\Upsilon = \{ \pm 1, \pm \omega, \pm \bar{\omega} \}
divisibility
\mathbf{y} | \mathbf{x} \text{ if } \exists \mathbf{z} \in \mathbb{Z}[\varkappa] \text{ such that } \mathbf{x} = \mathbf{y} \cdot \mathbf{z} \text{ and } \mathbf{y} \in \mathbb{Z}[\varkappa]
y∣x if ∃z∈Z[ϰ] such that x=y⋅z and y∈Z[ϰ]\mathbf{y} | \mathbf{x} \text{ if } \exists \mathbf{z} \in \mathbb{Z}[\varkappa] \text{ such that } \mathbf{x} = \mathbf{y} \cdot \mathbf{z} \text{ and } \mathbf{y} \in \mathbb{Z}[\varkappa]
greatest common divisor


 
\gcd(\mathbf{x}, \mathbf{y}) = \mathbf{z} \in \mathbb{Z}[\varkappa]\text{ is defined as a largest }
gcd(x,y)=z∈Z[ϰ] is defined as a largest \gcd(\mathbf{x}, \mathbf{y}) = \mathbf{z} \in \mathbb{Z}[\varkappa]\text{ is defined as a largest }
\mathbf{z} \in \mathbb{Z}[\varkappa]\text{ (up to multiplications by units) which }
z∈Z[ϰ] (up to multiplications by units) which \mathbf{z} \in \mathbb{Z}[\varkappa]\text{ (up to multiplications by units) which }
\text{divides both } \mathbf{x}\text{ and }\mathbf{y}
divides both x and y\text{divides both } \mathbf{x}\text{ and }\mathbf{y}
\text{Giving } a, b \in \mathbb{Z}\text{ and }\mathbf{x},\mathbf{y}, \in \mathbb{Z}[\varkappa], \varkappa \in \{i, \omega\}
Giving a,b∈Z and x,y,∈Z[ϰ],ϰ∈{i,ω}\text{Giving } a, b \in \mathbb{Z}\text{ and }\mathbf{x},\mathbf{y}, \in \mathbb{Z}[\varkappa], \varkappa \in \{i, \omega\}

Square grid

+ Memory addressing

+ Sampling is easy to define

Hexagonal grid

+ Uniform connectivity

+ Equidistant neighbors

+ Sampling is optimal

- Sampling is not optimal (ask bees)

- Neighbors are not equidistant

- Connectivity paradox

- Memory addressing is not trivial

- Sampling is difficult to define

Pros and Cons

Square grid

+ Memory addressing

+ Sampling is easy to define

Hexagonal grid

+ Uniform connectivity

+ Equidistant neighbors

+ Sampling is optimal

~ Memory addressing is not trivial

~ Sampling is difficult to define

Pros and Cons

- Sampling is not optimal (ask bees)

- Neighbors are not equidistant

~ Connectivity paradox

Digitization Model

A digitization cell of

0
00

denoted by

\mathcal{C}(0).
C(0).\mathcal{C}(0).

Digitization Model

The digitization operator is defined as

\mathcal{D}: \mathbb{C} \rightarrow \mathbb{Z}[\varkappa]
D:C→Z[ϰ]\mathcal{D}: \mathbb{C} \rightarrow \mathbb{Z}[\varkappa]

such that

\forall \mathbf{x} \in \mathbb{C}, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}[\varkappa]
∀x∈C,∃!D(x)∈Z[ϰ]\forall \mathbf{x} \in \mathbb{C}, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}[\varkappa]
\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).
x∈C(D(x)).\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).

and

\mathbf{p}
p\mathbf{p}
\mathbf{k}
k\mathbf{k}

From Continuous to Discrete

Neighborhood Motion Maps

Image from page 114 of "Coloured illustrations of British birds, and their eggs" (1842)

Bijective Digitized Rotations on Hexagonal Lattice

Image from page 339 of "The natural history of British insects"

Conditions for Bijectivity

Conditions for Bijectivity

A digitized rotation is bijective if and only if

\forall \mathbf{p} \in \mathbb{Z}[\omega] \; \exists ! \mathbf{q} \in \mathbb{Z}[\omega]
∀p∈Z[ω]∃!q∈Z[ω]\forall \mathbf{p} \in \mathbb{Z}[\omega] \; \exists ! \mathbf{q} \in \mathbb{Z}[\omega]

such that

\mathcal{U}(\mathbf{q}) \in \mathcal{C}(\mathbf{p}).
U(q)∈C(p).\mathcal{U}(\mathbf{q}) \in \mathcal{C}(\mathbf{p}).
\mathcal{U}
U\mathcal{U}

- a continuous rotation

\mathcal{C}(\mathbf{p})
C(p)\mathcal{C}(\mathbf{p})

- a digitization cell centered at

\mathbf{p}
p\mathbf{p}
\mathbb{Z}[\omega]
Z[ω]\mathbb{Z}[\omega]

- the hexagonal lattice

Conditions for Bijectivity

"Double" Surjectivity Condition for Bijectivity

\mathbf{a} \in \mathbb{C}
a∈C\mathbf{a} \in \mathbb{C}
\mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(\mathcal{U}(\mathbf{q}))
Ca∣a∣(U(q))\mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(\mathcal{U}(\mathbf{q}))

- a complex number

- a rotated digitization cell

Set of Remainders

The "double" surjectivity condition is then

provided that

S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_1(0) = S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(0).
Sa(Z[ω],Z[ω])∩C1(0)=Sa(Z[ω],Z[ω])∩Ca∣a∣(0).S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_1(0) = S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(0).

Set of Remainders

The "double" surjectivity condition is then

provided that

S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\mathbf{a}}(0) = S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{|\mathbf{a}|}(0).
Sa(Z[ω],Z[ω])∩Ca(0)=Sa(Z[ω],Z[ω])∩C∣a∣(0).S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\mathbf{a}}(0) = S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{|\mathbf{a}|}(0).

Factorization of Primitive Eisenstein Integers

s, t \in \mathbb{Z}
s,t∈Zs, t \in \mathbb{Z}
0 < s < t
0<s<t0 < s < t

and

t - s
t−st - s

not being divisible by 3.

a = s^2 + 2 s t, b = t^2 + 2 s t
a=s2+2st,b=t2+2sta = s^2 + 2 s t, b = t^2 + 2 s t

and

c = s^2 + t^2 + s t,
c=s2+t2+st,c = s^2 + t^2 + s t,

such that

Factorization of Primitive Eisenstein Integers

A bunch of facts

Set of Remainders

The "double" surjectivity condition is then

provided that

Proving Bijectivity

Proving Bijectivity

Step 1: For which s and t,

or

are in the green but not in

the black hexagonal cell.

Proving Bijectivity

Proving Bijectivity

From the equation of the green line we obtain:

Proving Bijectivity

From the equation of the green line we obtain:

Then, we substitute t with s + e to arrive at

which are violated when s = 1 or when s > 1 and e = 1.

Proving Bijectivity

There are few more things to check in this step. See the manuscript (Lemma 5.3)/article (Lemma 7).

Proving Bijectivity

Step 2: Check if for s = 1 or s > 1 and e = 1, the uncommon space of the hexagonal cells does not contain Eisenstein integers.

s = 1
s=1s = 1
s > 1, t = s + 1
s>1,t=s+1s > 1, t = s + 1

Proving Bijectivity

The Square Grid

The Hexagonal Grid

Neighborhood

The neighborhood of

\mathbf{p} \in \mathbb{Z}[\varkappa]
p∈Z[ϰ]\mathbf{p} \in \mathbb{Z}[\varkappa]

(of squared radius

r \in \mathbb{R}_+
r∈R+r \in \mathbb{R}_+

):

\mathcal{N}_r(\mathbf{p}) = \big\{ \mathbf{p} + \mathbf{d} \in \mathbb{Z}[\varkappa] \mid |\mathbf{d} |^2 \leq r \big\}
Nr(p)={p+d∈Z[ϰ]∣∣d∣2≤r}\mathcal{N}_r(\mathbf{p}) = \big\{ \mathbf{p} + \mathbf{d} \in \mathbb{Z}[\varkappa] \mid |\mathbf{d} |^2 \leq r \big\}

Neighborhood Motion Maps

r \in \mathbb{R}_+
r∈R+r \in \mathbb{R}_+
U
UU

and

\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
∣GrU:Nr(0)→Nr′(0)d↦U(p+d)−U(p).\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
\mathbf{p}
p\mathbf{p}
\mathbf{p}
p\mathbf{p}

The neighborhood motion map of

\mathbf{p} \in \mathbb{Z}[\varkappa]
p∈Z[ϰ]\mathbf{p} \in \mathbb{Z}[\varkappa]

for a given rigid motion

Neighborhood Motion Maps

r \in \mathbb{R}_+
r∈R+r \in \mathbb{R}_+
U
UU

and

\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
∣GrU:Nr(0)→Nr′(0)d↦U(p+d)−U(p).\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
\mathbf{p}
p\mathbf{p}
\mathbf{p}
p\mathbf{p}

The neighborhood motion map of

\mathbf{p} \in \mathbb{Z}[\varkappa]
p∈Z[ϰ]\mathbf{p} \in \mathbb{Z}[\varkappa]

for a given rigid motion

Neighborhood Motion Maps

The neighborhood motion map of

\mathbf{p} \in \mathbb{Z}[\varkappa]
p∈Z[ϰ]\mathbf{p} \in \mathbb{Z}[\varkappa]

for a given rigid motion

r \in \mathbb{R}_+
r∈R+r \in \mathbb{R}_+
U
UU

and

\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
∣GrU:Nr(0)→Nr′(0)d↦U(p+d)−U(p).\left| \begin{array}{lllll} \mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\ & & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}). \end{array} \right.
\mathbf{p}
p\mathbf{p}
\mathbf{p}
p\mathbf{p}

Remainder Map Step-by-Step

\mathbf{p}
p\mathbf{p}

Remainder Map step-by-step

\mathbf{p}
p\mathbf{p}

Remainder Map Step-by-Step

\mathcal{U}(\mathbf{p} + \mathbf{d}) =
U(p+d)=\mathcal{U}(\mathbf{p} + \mathbf{d}) =
\mathbf{a} \cdot \mathbf{d}
a⋅d\mathbf{a} \cdot \mathbf{d}
+\ \mathcal{U}(\mathbf{p})
+ U(p)+\ \mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p} + \mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p} + \mathbf{d})

Remainder Map Step-by-Step

\mathcal{U}(\mathbf{p} + \mathbf{d}) =
U(p+d)=\mathcal{U}(\mathbf{p} + \mathbf{d}) =
\mathbf{a} \cdot \mathbf{d}
a⋅d\mathbf{a} \cdot \mathbf{d}
+\ \mathcal{U}(\mathbf{p})
+ U(p)+\ \mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p} + \mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p} + \mathbf{d})
U(\mathbf{p})
U(p)U(\mathbf{p})
\mathcal{U}(\mathbf{p})
U(p)\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p}+\mathbf{d})

Remainder Map Step-by-Step

Without loss of generality,

U(\mathbf{p})
U(p)U(\mathbf{p})

is the origin, and then

\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(d)=a⋅d+U(p)−U(p)\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
\mathbf{a} \cdot \mathbf{d}
a⋅d\mathbf{a} \cdot \mathbf{d}
\mathbf{d}
d\mathbf{d}
\mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(p)−U(p)\mathcal{U}(\mathbf{p}) - U(\mathbf{p})

Remainder Map Step-by-Step

Without loss of generality,

U(\mathbf{p})
U(p)U(\mathbf{p})

is the origin, and then

\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(d)=a⋅d+U(p)−U(p)\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
\mathbf{a} \cdot \mathbf{d}
a⋅d\mathbf{a} \cdot \mathbf{d}
\mathbf{d}
d\mathbf{d}
\mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(p)−U(p)\mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(\mathbf{p})
U(p)U(\mathbf{p})
\mathcal{U}(\mathbf{p})
U(p)\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p}+\mathbf{d})

Remainder Map Step-by-Step

The remainder map defined as

\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})
F(p)=U(p)−U(p)∈C(0)\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})

 where the range

\mathcal{C}(\mathbf{0})
C(0)\mathcal{C}(\mathbf{0})

is called the remainder range.

\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
F(p)=U(p)−U(p)\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})

Remainder Map Step-by-Step

The remainder map defined as

\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})
F(p)=U(p)−U(p)∈C(0)\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})

 where the range

\mathcal{C}(\mathbf{0})
C(0)\mathcal{C}(\mathbf{0})

is called the remainder range.

\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
F(p)=U(p)−U(p)\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(\mathbf{p})
U(p)U(\mathbf{p})
\mathcal{U}(\mathbf{p})
U(p)\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p}+\mathbf{d})

Remainder Map and Critical Rigid Motions

Remainder Map and Critical Rigid Motions

U(\mathbf{p})
U(p)U(\mathbf{p})
\mathcal{U}(\mathbf{p})
U(p)\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
U(p+d)\mathcal{U}(\mathbf{p}+\mathbf{d})

Such critical cases can be observed via the relative positions of         ,

\mathcal{F}(\mathbf{p})
F(p)\mathcal{F}(\mathbf{p})
\mathcal{H} - \mathbf{a} \cdot \mathbf{d}
H−a⋅d\mathcal{H} - \mathbf{a} \cdot \mathbf{d}

That is to say

\mathcal{C}(\mathbf{0}) \cap (\mathcal{H} - \mathbf{a} \cdot \mathbf{d}).
C(0)∩(H−a⋅d).\mathcal{C}(\mathbf{0}) \cap (\mathcal{H} - \mathbf{a} \cdot \mathbf{d}).

and are formulated as the translations                .

Remainder Map and Critical Rigid Motions

\mathcal{H} - \mathbf{a} \cdot \mathbf{d}
H−a⋅d\mathcal{H} - \mathbf{a} \cdot \mathbf{d}

Critical Lines

\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
H=⋃d∈Nr(0)(H−a⋅d)∩C(0)\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)

Critical Lines

\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
H=⋃d∈Nr(0)(H−a⋅d)∩C(0)\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)

Critical Line Segments

\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
H=⋃d∈Nr(0)(H−a⋅d)∩C(0)\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)

Frames

Each region bounded by the critical line segments is called a frame.

Frames

Each region bounded by the critical line segments is called a frame.

Frames

Each region bounded by the critical line segments is called a frame.

Frames

For any

\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})
p,q∈Z[ϰ],GrU(p)=GrU(q)\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})

if and only if

\mathcal{F}(\mathbf{p})
F(p)\mathcal{F}(\mathbf{p})

and

\mathcal{F}(\mathbf{q})
F(q)\mathcal{F}(\mathbf{q})

the same frame.

Proposition

are in

Frames

For any

\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})
p,q∈Z[ϰ],GrU(p)=GrU(q)\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})

if and only if

\mathcal{F}(\mathbf{p})
F(p)\mathcal{F}(\mathbf{p})

and

\mathcal{F}(\mathbf{q})
F(q)\mathcal{F}(\mathbf{q})

the same frame.

Proposition

are in

Remainder Range Partitioning

At most 25 frames per partitioning.

Remainder Range Partitioning

At most 81 frames per partitioning.

Remainder Range Partitioning

At most 49 frames per partitioning.

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Neighborhood Motion Maps Graph

Preservation of Information

Image taken from page 371 of 'Lahore to Yārkand. Incidents of the route and natural history of the countries traversed by the expedition of 1870, under T. D. Forsyth, etc'

Non-injective and Non-surjective Digitized Rigid Motions

Non-injective and Non-surjective Digitized Rigid Motions

Non-injective and Non-surjective Digitized Rigid Motions

Loss of Information

\mathcal{F}(\mathbb{Z}[i])
F(Z[i])\mathcal{F}(\mathbb{Z}[i])

Pythagorean Rotations

If

\cos\theta
cosθ\cos\theta

and

\sin\theta
sinθ\sin\theta

are rational numbers, then the remainder map has

a finite number of images.

\mathcal{F}(\mathbb{Z}[i])
F(Z[i])\mathcal{F}(\mathbb{Z}[i])

Pythagorean Rotations

There exists a one-to-one relation between primitive Pythagorean

Lemma

triples:

(a,b,c) \in \mathbb{Z}^3, a < b < c \text{ and } \gcd(a,b,c) = 1
(a,b,c)∈Z3,a<b<c and gcd(a,b,c)=1(a,b,c) \in \mathbb{Z}^3, a < b < c \text{ and } \gcd(a,b,c) = 1

and rational

rotations.

\mathcal{F}(\mathbb{Z}[i])
F(Z[i])\mathcal{F}(\mathbb{Z}[i])

Pythagorean Rotations

Such primitive Pythagorean triples can be generated from:

p, q \in \mathbb{Z}
p,q∈Zp, q \in \mathbb{Z}

such that

0 < q < p
0<q<p0 < q < p

and

p - q
p−qp - q

being odd.

Finally,

a = p^2 - q^2, b = 2 p q
a=p2−q2,b=2pqa = p^2 - q^2, b = 2 p q

and

c = p^2 + q^2.
c=p2+q2.c = p^2 + q^2.
\mathcal{F}(\mathbb{Z}[i])
F(Z[i])\mathcal{F}(\mathbb{Z}[i])

Pythagorean Rotations

The number of images of the remainder map is equal to

Corollary

c\text{.}
c.c\text{.}
\mathcal{F}(\mathbb{Z}[\omega])
F(Z[ω])\mathcal{F}(\mathbb{Z}[\omega])

For what kinds of parameters has the remainder map a finite number of images? 

Eisenstein Rational Rotations

Eisenstein Rational Rotations

If

\cos\theta = \frac{2a -b}{2 c}
cosθ=2a−b2c\cos\theta = \frac{2a -b}{2 c}

and

\sin\theta = \frac{\sqrt{3}b}{2 c}
sinθ=3b2c\sin\theta = \frac{\sqrt{3}b}{2 c}

where

(a,b,c)\in \mathbb{Z}^3, \gcd(a,b,c) = 1
(a,b,c)∈Z3,gcd(a,b,c)=1(a,b,c)\in \mathbb{Z}^3, \gcd(a,b,c) = 1

and

0 < a < c < b,
0<a<c<b,0 < a < c < b,

Proposition

then the remainder map has a finite number

of images equal to

\mathcal{F}(\mathbb{Z}[\omega])
F(Z[ω])\mathcal{F}(\mathbb{Z}[\omega])
c\text{.}
c.c\text{.}

Eisenstein Rational Rotations

\mathcal{F}(\mathbb{Z}[\omega])
F(Z[ω])\mathcal{F}(\mathbb{Z}[\omega])

is a primitive Eisenstein triple which can be

s, t \in \mathbb{Z}
s,t∈Zs, t \in \mathbb{Z}

such that

0 < s < t
0<s<t0 < s < t

and

t - s
t−st - s

not being

divisible by 3. Finally,

a = s^2 + 2 s t, b = t^2 + 2 s t
a=s2+2st,b=t2+2sta = s^2 + 2 s t, b = t^2 + 2 s t

and

c = s^2 + t^2 + s t.
c=s2+t2+st.c = s^2 + t^2 + s t.
(a,b,c) \in \mathbb{Z}^3
(a,b,c)∈Z3(a,b,c) \in \mathbb{Z}^3

Such

generated from:

Loss of Information

Bijective Digitized Rigid Motions on Square Grid

Image from page 209 of "Coloured illustrations of British birds, and their eggs" (1842)

Which Digitized Rigid Motions are Bijective?

Question 1: Can non-rational rigid motions be bijective?

Question 1: Can non-rational rigid motions be bijective?

Question 2: Can a non-bijective rational rotation followed by a translation be bijective?

Globally Bijective Digitized Rigid Motions

Globally Bijective Digitized Rigid Motions

Question 3: What are the possible translations which can be applied with a bijective digitized rotation?

f_\downarrow^0
f↓0f_\downarrow^0
c
cc
s
ss
r
rr
w
ww

What are the possible translations which can follow a bijective digitized rotation?

What are the possible translations which can follow a bijective digitized rotation?

\phi
ϕ\phi
\psi
ψ\psi

What are the possible translations which can follow a bijective digitized rotation?

c
cc
s
ss
r
rr
w
ww

A digitized rigid motion is bijective if and only if it is composed of a rotation by an angle defined by a twin Pythagorean triple (a, b, c) and a translation

\mathbf{t} = \mathbf{t}' + \mathbb{Z}\psi + \mathbb{Z}\phi,
t=t′+Zψ+Zϕ,\mathbf{t} = \mathbf{t}' + \mathbb{Z}\psi + \mathbb{Z}\phi,
\phi
ϕ\phi
\psi
ψ\psi

where

\mathbf{t}' \in \left(-\frac{1}{2c}, \frac{1}{2c}\right) \oplus \left(-\frac{1}{2c}, \frac{1}{2c} \right) i.
t′∈(−12c,12c)⊕(−12c,12c)i.\mathbf{t}' \in \left(-\frac{1}{2c}, \frac{1}{2c}\right) \oplus \left(-\frac{1}{2c}, \frac{1}{2c} \right) i.

Proposition

Bijective Digitized Rigid Motions of Finite Subsets of The Square Grid

Image from page 126 of "Coloured illustrations of British birds, and their eggs" (1842)

\mathbb{Z}[i]
Z[i]\mathbb{Z}[i]

Is a given digitized rigid motion bijective when restricted to a finite subset of

?

Bijective Digitized Rigid Motions Are Not Dense

\mathcal{F}(S)
F(S)\mathcal{F}(S)

Forward Algorithm

\mathcal{F}(S)
F(S)\mathcal{F}(S)

Forward Algorithm

\text{Complexity: } \mathcal{O}(|S|)
Complexity: O(∣S∣)\text{Complexity: } \mathcal{O}(|S|)

Backward Algorithm - Step 1

Backward Algorithm - Step 1

\phi
ϕ\phi
\psi
ψ\psi
(-1,3)
(−1,3)(-1,3)
(-1,3)
(−1,3)(-1,3)

Backward Algorithm - Step 2

Backward Algorithm - Step 2

Backward Algorithm - Step 3

Backward Algorithm - Step 3

\text{Complexity: } \mathcal{O}(q) + \mathcal{O}(\log \min(a,b)) + \mathcal{O}(\sqrt{|S|})
Complexity: O(q)+O(logmin(a,b))+O(∣S∣)\text{Complexity: } \mathcal{O}(q) + \mathcal{O}(\log \min(a,b)) + \mathcal{O}(\sqrt{|S|})

Step 1

Step 2

Step 3

Forward

Depends on the size of the finite set

Backward

Depends on the square root of the finite set size and the parameters of the rational rotations

Backward vs. Forward Algorithm

Backward vs. Forward Algorithm

When the size of the finite set is relatively low and the number of elements in the non-injective zones is relatively high, the forward algorithm is usually a better choice than the backward algorithm and vice versa.

Finding Local Bijectivity Angle Interval

Finding Local Bijectivity Angle Interval

\mathcal{F}(S)
F(S)\mathcal{F}(S)

Finding Local Bijectivity Angle Interval

U(S)
U(S)U(S)

What are the intervals of the parameters around the initial ones such that the corresponding transformations remain bijective when restricted to the set?

Our strategy in short: Fix the translation and then find a rotation angles interval using the notion of "hinge angles".

Finding Local Bijectivity Angle Interval

Finding Local Bijectivity Angle Interval

\cos \alpha = \frac{p_1 \lambda + p_2 \left(k + \frac{1}{2} \right)}{p_1^2 + p_2^2}
cosα=p1λ+p2(k+12)p12+p22\cos \alpha = \frac{p_1 \lambda + p_2 \left(k + \frac{1}{2} \right)}{p_1^2 + p_2^2}
\lambda = \sqrt{p_1^2 + p_2^2 - \left(k + \frac{1}{2} \right)^2}
λ=p12+p22−(k+12)2\lambda = \sqrt{p_1^2 + p_2^2 - \left(k + \frac{1}{2} \right)^2}

Finding Local Bijectivity Angle Interval

Finding Local Bijectivity Angle Interval

\cos \alpha = \frac{p_1 \lambda + p_2 \left(k - t_2 + \frac{1}{2} \right)}{p_1^2 + p_2^2}
cosα=p1λ+p2(k−t2+12)p12+p22\cos \alpha = \frac{p_1 \lambda + p_2 \left(k - t_2 + \frac{1}{2} \right)}{p_1^2 + p_2^2}
\lambda = \sqrt{p_1^2 + p_2^2 - \left(k - t_2 + \frac{1}{2} \right)^2}
λ=p12+p22−(k−t2+12)2\lambda = \sqrt{p_1^2 + p_2^2 - \left(k - t_2 + \frac{1}{2} \right)^2}

Finding Local Bijectivity Angle Interval

Finding Local Bijectivity Angle Interval

Finding Local Bijectivity Angle Interval

Part II:

3D Discrete Spaces

Introduction to 3D Digital Geometry

Image from page 27 of "A history of British birds. By the Rev. F.O. Morris .." (1862)

The Cubic Grid

The cubic lattice is then:

Digitization Model

A digitization cell of

\mathbf{x}
x\mathbf{x}

denoted by

\mathcal{C}(\mathbf{x}).
C(x).\mathcal{C}(\mathbf{x}).

Digitization Model

The digitization operator is defined as

\mathcal{D}: \mathbb{R}^3 \rightarrow \mathbb{Z}^3
D:R3→Z3\mathcal{D}: \mathbb{R}^3 \rightarrow \mathbb{Z}^3

such that

\forall \mathbf{x} \in \mathbb{R}^3, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}^3
∀x∈R3,∃!D(x)∈Z3\forall \mathbf{x} \in \mathbb{R}^3, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}^3
\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).
x∈C(D(x)).\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).

and

Quick Introduction to 3D Rigid Motions

Image from page 358 of "A general history of birds" (1821)

\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{R}^3 & \to & \mathbb{R}^3 \\ & & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t} \end{array} \right.
∣U:R3→R3x↦Rx+t\left| \begin{array}{lllll} \mathcal{U} & : & \mathbb{R}^3 & \to & \mathbb{R}^3 \\ & & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t} \end{array} \right.

Rigid Motions on

\mathbb{R}^3
R3\mathbb{R}^3

Properties

  • Do preserve distances

  • Bijective

\mathbf{R}
R\mathbf{R}

- rotation matrix

\mathbf{t}
t\mathbf{t}

- translation vector

U = \mathcal{D}\ \circ \mathcal{U}_{|\mathbb{Z}^3}
U=D ∘U∣Z3U = \mathcal{D}\ \circ \mathcal{U}_{|\mathbb{Z}^3}

Properties

  • Non-injective
  • Non-surjective
  • Do not preserve distances
\mathcal{U}(\mathbb{Z}^3)
U(Z3)\mathcal{U}(\mathbb{Z}^3)

Digitized Rigid Motions

Contributions in Short

  • An algorithm to characterize bijective digitized rotations
     
  • An algorithm to compute all possible images of a finite digital set under digitized rigid motions

I am Going to Talk About

An algorithm to characterize bijective digitized rotations

Spatial Rotations and Quaternions

Image from page 618 of "The Ibis" (1859)

Spatial Rotations and Quaternions

\mathbb{H} = \{a + b i + c j + d k | a,b,c,d \in \mathbb{R} \}
H={a+bi+cj+dk∣a,b,c,d∈R}\mathbb{H} = \{a + b i + c j + d k | a,b,c,d \in \mathbb{R} \}

with

i^2 = j^2 = k^2 = i j k = {-1}
i2=j2=k2=ijk=−1i^2 = j^2 = k^2 = i j k = {-1}

Properties:

  • Hamilton product is not commutative
     
  • Any rotation can be written as
\mathcal{U} : \mathbf{x} \mapsto q \mathbf{x} q^{-1}
U:x↦qxq−1\mathcal{U} : \mathbf{x} \mapsto q \mathbf{x} q^{-1}

where

q \in \mathbb{H}, \mathbf{x} \in \mathbb{R}^3
q∈H,x∈R3q \in \mathbb{H}, \mathbf{x} \in \mathbb{R}^3
  • We can derive a rotation matrix

where

K = a^2 + b^2 + c^2 + d^2
K=a2+b2+c2+d2K = a^2 + b^2 + c^2 + d^2

The figure source: http://www.3dgep.com/understanding-quaternions/

Bijectivity of 3D Digitized Rotations

Image from A history of the birds of Europe, not observed in the British Isles

Bijectivity of 3D Digitized Rotations

Remainders

3D digitized rotation is then
bijective when

\forall \mathbf{y} \in \mathbb{Z}^3\ \exists! \mathbf{x} \in \mathbb{Z}^3, S_q(\mathbf{x},\mathbf{y}) \in \mathcal{C}(\mathbf{0})
∀y∈Z3 ∃!x∈Z3,Sq(x,y)∈C(0)\forall \mathbf{y} \in \mathbb{Z}^3\ \exists! \mathbf{x} \in \mathbb{Z}^3, S_q(\mathbf{x},\mathbf{y}) \in \mathcal{C}(\mathbf{0})

Remainders

Equivalently and more computationally friendly (we will see later)

such that

S_{q}(\mathbb{Z}^3,\mathbb{Z}^3) \cap ((\mathcal{C}(\mathbf{0}) \cup q \mathcal{C}(\mathbf{0}) q^{-1}) \setminus (\mathcal{C}(\mathbf{0}) \cap q \mathcal{C}(\mathbf{0}) q^{-1})) = \varnothing
Sq(Z3,Z3)∩((C(0)∪qC(0)q−1)∖(C(0)∩qC(0)q−1))=∅ S_{q}(\mathbb{Z}^3,\mathbb{Z}^3) \cap ((\mathcal{C}(\mathbf{0}) \cup q \mathcal{C}(\mathbf{0}) q^{-1}) \setminus (\mathcal{C}(\mathbf{0}) \cap q \mathcal{C}(\mathbf{0}) q^{-1})) = \varnothing

Group Spanned by Values of

S_q
SqS_q

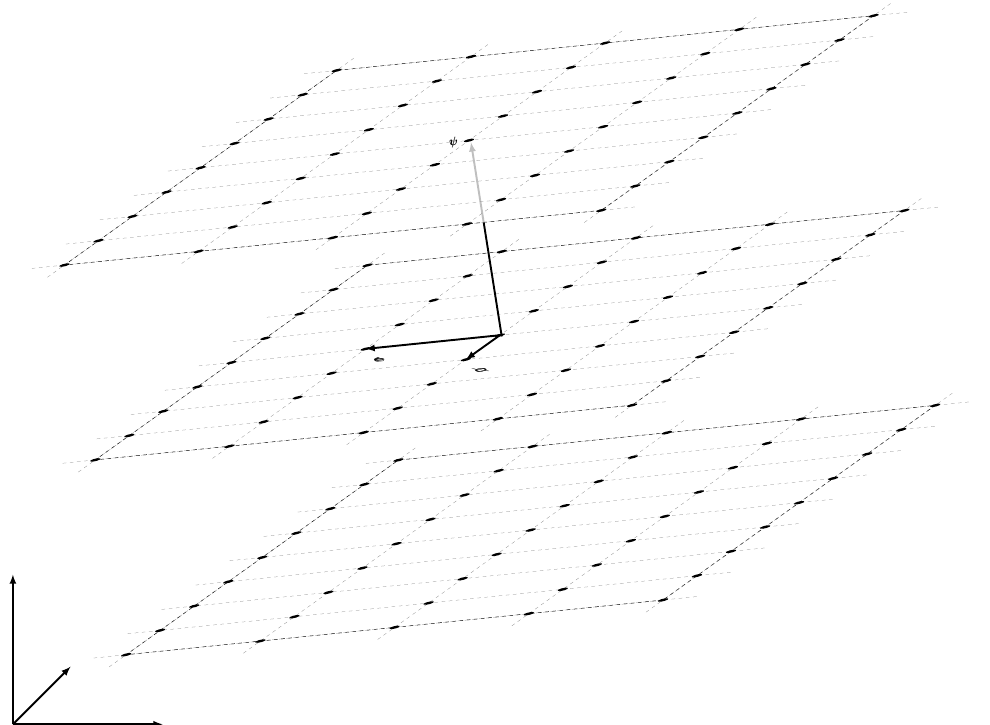
Proposition

If all the generators of

\mathcal{G}_q
Gq\mathcal{G}_q

have only rational terms, then there exist vectors

which are the

minimal generators of

\mathcal{G}_q.
Gq.\mathcal{G}_q.

Group Spanned by Values of

S_q
SqS_q

Lemma

If

\mathcal{G}_q
Gq\mathcal{G}_q

is dense, then the

corresponding 3D digitized rotation is not bijective.

Group Spanned by Values of

S_q
SqS_q

Conjecture

If

\mathcal{G}_q
Gq\mathcal{G}_q

has a dense factor,

the corresponding digitized rotation is not bijective.

Lipschitz Quaternions and Rational Rotations

Proposition

There is a two-to-one correspondence between the set of Lipschitz quaternions

\mathbb{L} = \{ a+ b i + c j + d k | a,b,c,d \in \mathbb{Z}\}
L={a+bi+cj+dk∣a,b,c,d∈Z}\mathbb{L} = \{ a+ b i + c j + d k | a,b,c,d \in \mathbb{Z}\}

such that the

\gcd(a,b,c,d) = 1,
gcd(a,b,c,d)=1,\gcd(a,b,c,d) = 1,

and the set of rational rotations.

where

K = a^2 + b^2 + c^2 + d^2.
K=a2+b2+c2+d2.K = a^2 + b^2 + c^2 + d^2.
\mathbf{R} =
R=\mathbf{R} =

Bijectivity Characterization Algorithm

Image from page 187 of "Coloured illustrations of British birds, and their eggs" (1842)

Turning into Integers

Since we have

q \cdot \mathbf{x} \cdot q^{-1}
q⋅x⋅q−1q \cdot \mathbf{x} \cdot q^{-1}

where

q^{-1} = \frac{\bar{q}}{|q|^2}
q−1=q¯∣q∣2q^{-1} = \frac{\bar{q}}{|q|^2}

and

\mathcal{G}_q
Gq\mathcal{G}_q

is rational, we can

multiply by

|q|^2
∣q∣2|q|^2

and obtain an integer lattice.

Reducing the Left Factor

We are allowed to divide on the left by q while keeping integer valued functions.

Characterization Algorithm Step 1

To check if

\mathbf{w} \in \mathbb{Z}^4
w∈Z4\mathbf{w} \in \mathbb{Z}^4

belongs to values

of

S'_{q},
Sq′,S'_{q},

first verify whether

a w_1 - b w_2 - c w_3 - d w_4 = 0
aw1−bw2−cw3−dw4=0a w_1 - b w_2 - c w_3 - d w_4 = 0

Characterization Algorithm Step 2

Then we solve the following Diophantine system:

\mathbf{Az} = \mathbf{w}
Az=w\mathbf{Az} = \mathbf{w}

where

\mathbf{z}^t = (\mathbf{x}, \mathbf{y}) \in \mathbb{Z}^6
zt=(x,y)∈Z6\mathbf{z}^t = (\mathbf{x}, \mathbf{y}) \in \mathbb{Z}^6

and

The complexity of reducing

\mathbf{A} \text{ is } \mathcal{O}(\log^2N(\mathbf{A})).
A is O(log2N(A)).\mathbf{A} \text{ is } \mathcal{O}(\log^2N(\mathbf{A})).

The final complexity is

\mathcal{O}(|q|^3 + \log^2N(\mathbf{A})).
O(∣q∣3+log2N(A)).\mathcal{O}(|q|^3 + \log^2N(\mathbf{A})).

Some Experimental Results

Image from page 45 of "The natural history of British birds, or, A selection of the most rare, beautiful and interesting birds which inhabit this country

For more see: https://perso.esiee.fr/~plutak/projects/2017-06-06-3d-bij

Conclusion and Perspectives

  • A general framework to study 2D digitized rigid motions
  • Comparison of the digitized rigid motions defined on square and hexagonal lattices
  • Characterization of bijective digitized:
    • rigid motions on the square grid
    • rotations on the hexagonal grid
    • 3D rotations on the cubic grid
  • Algorithms to characterize if a digitized rigid motion is bijective when restricted to a finite set
  • An algorithm to compute, under 3D digitized rigid motions, all possible images of a finite digital set

Conclusion

Conclusion and Perspectives

  • Analytical characterization of 3D bijective rigid motions
  • Extension of the study to the triangular grid

  • Identification of minimal 3D sets that break 6-connectivity under digitized rigid motions

Perspectives

Made with Slides.com