What is
functional programming about?
first class functions?
immutable data?
referential transparency?
composition!
A => C
A => B
B => C
g • f : A => C
g : B =>C
f : A =>B
def compose( f: A =>B, g: B=>C ) : A =>C
(a: A) => g(f(a))
It's trivial, isn't it?
Why is this not used all the time?
Scenario 1: f returns null
val v = f(a)
if( v != null) g(v)
Scenario 2: f throws exceptions
try {
val v = f(a)
g(v)
} catch e {
print( "(╯°□°)╯︵ ┻━┻ " )
}
Scenario 3: f is asynchronous
f(a, callback = { b => g(b)
})
So, is it impractical to model programs as function compositions?
Of course not.
First, let's use types to make things explicit.
Scenario 1: f returns null
f: A => Option[B]
Option[T] : Some(t) | None
Scenario 2: f throws exceptions
f: A => Either[E, B]
Either[E, T]: Left(e) | Right[T]
Scenario 3: f is asynchronous
f: A => Future[B]
Future(b).callback(f: B => C)
In all these scenarios, f returns a "container" of B
f: A => F[B]
Noticed the pattern?
A => F[C]
g : B =>C
f : A =>F[B]
?
So, the problem generalizes to:
def composeF( f: A =>F[B], g: B=>C ) : A =>F[C]
(a: A) =>
val fb : F[B] = f(a)
val fg: F[B] => F[C] = ???(g)
fg(fb)
def lift(g: A => R) : F[A] => F[R]
A => F[C]
g : B =>C
f : A =>F[B]
lift(f: A =>R): F[A] => F[R]
So, for whatever F, if we can define a lift, we can compose (likely)!
def lift (f: A => B) : Option[A] => Option[B] =
(oa: Option[A]) => oa match {
case Some(a) => Some(f(a))
case None => None
}
lift for Option
def lift (f: A => B) : Either[E, A] => Either[E, B] =
(oa: Either[A]) => oa match {
case Right(a) => Right(f(a))
case Left(e) => Left(e)
}
lift for Either
def map(fa: F[A], f: A => B) : F[B]
In fact, there's a familiar
form of lift:
List(1, 2, 3).map(i => i + 1)
//returns List(2, 3, 4)
def lift(f: A => B) : F[A] => F[B] =
(fa: F[A]) => map(fa, f)
lift can be implemented with map and vice versa
Would any lift work?
No. Here are some counter examples:
-
a lift of Option that flips Some and None.
-
a lift of List that shrinks the list size.
I.E. would any lift enable the composition?
So, to enable composition, lift must preserve the "structure" of F.
How do we formally describe this rule? Can we describe it without referring to the actual structure of F?
Category Theory
A branch of mathematics that studies the relationships between objects and the composition of them without looking into the objects.
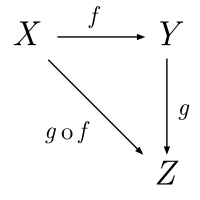
g • f : A => C
g : B =>C
f : A =>B
( A =>B ) => ( F[A] => F[B] )
A F with a lift proper for composition is
Functor
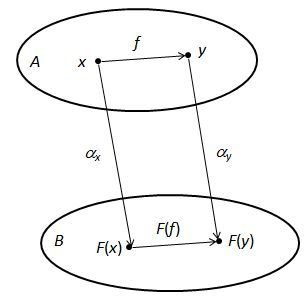
Functor Laws
lift(g) • lift(f) == lift(g•f)
Category theory provides a set of laws for a proper lift of a functor, which are all about the functions rather than the structure.
-
Identity -
Composition
A => F[C]
g : B =>C
f : A =>F[B]
?
g : B =>F[C]
def composeM(f: A =>M[B], g: B=>M[C]): A =>M[C]
(a: A) =>
val mb : M[B] = f(a)
val mg : M[B] => M[M[C]] = lift(g)
val mmc : M[M[C]] = fg(mb)
def flatten(mma: M[M[A]]) : M[A]
???(mmc)
A => M[C]
g : B =>M[C]
f : A =>M[B]
lift(f: A =>B): M[A] => M[B]
So, for whatever M, if we can define a lift and a flatten, we can compose (likely)!
flatten(mma: M[M[A]]) : M[A]
def flatten(ooa: Option[Option[A]]) : Option[A] =
(oa: Option[Option[A]]) => oa match {
case Some(Some(a)) => Some(a)
case _ => None
}
flatten for Option
def flatMap(fa: M[A], f: A => M[B]) : M[B]
In fact there's also a familiar
form of flatten:
List(1, 2, 3).flatMap(i => List(1*i, 2*i))
// List(1, 2, 2, 4, 3, 6)
flatten can be implemented with flatMap and vice versa
def flatten(fa: M[M[A]]) : M[A] =
flatMap(fa, t => t)
Would any flatten work?
No, like lift, flatten also needs to preserve the structure of M.
How do we describe this rule for flatten?
A => M[A]
Monad
Is there a thing in category theory that defines a flatten on top of a Functor?
Monad requires one more operation pure:
Monad
And you guessed it, category theory provides a set of Monad laws for proper flatten and pure implementations.
-
Left Identity -
Right Identity -
Associativity
Monadic composition in practice
f: A => M[B], g: B => M[C], e: C => M[D]
composed: A => M[D] = f andThen g andThen e
composed(a)
f(a).flatMap(g).flatMap(e)
f(a).flatMap( b => g(b).flatMap(c => e(c)))
flatMap: (M[A], A => M[B]) => M[B]
Monadic composition in practice
f: A => M[B], g: B => M[C], e: (B, C) => M[D]
f(a).flatMap( b => g(b).flatMap(c => e(b, c)))
for {
b <- f(a)
c <- g(b)
d <- e(b, c)
} yield d
Syntax sugar from language (scala, haskell)
Real world Monadic composition
def create(abtest: Abtest): Result[Entity[Abtest]] = for {
validated <- validate(abtest)
checked <- checkConflict(validated)
r <- dao.insert(checked)
} yield r
Asynchronous operations with proper error handling composed by simply laying down the happy path
Conclusion
Functional programming is about applying category theory to help enable composition.
Next Steps
To learn category theory, Bartosz Milewski offers a great series of video lectures of category theory for programers. https://www.youtube.com/playlist?list=PLbgaMIhjbmEnaH_LTkxLI7FMa2HsnawM_ It's the main inspiration of this talk.
To learn functional programming in scala, cats is a library providing FP structures like Functor and Monad. http://github.com/typelevel/cats Here is a book about it: Advanced Scala with Cats http://underscore.io/books/advanced-scala/
Questions?