GPUs, Graphics, and Rays

Kai Ninomiya
for DSC IZTECH

slides.com/kainino/ggr

Me

  • Currently: Chrome WebGPU/WebGL Team, Google
    • Focusing on standardization and implementation of WebGPU
      • ​An upcoming Web standard API (like WebGL) for modern GPU acceleration
    • (This is a personal presentation; I don't speak for Google)
slides.com/kainino/ggr

Me

  • Past: University of Pennsylvania 2011-2016
    • BSE+MSE Computer Science (graphics focus, physics minor)
    • Co-instructor for courses on Linux/Unix Skills and Rust and teaching assistant for several courses including CIS 565, GPU Programming and Architecture
      • ​Which is where I learned most of this stuff! Go look up their slides!
    • Sysadmin for a residential program
  • ​Originally from the U.S. east coast
slides.com/kainino/ggr

This Presentation

Follow along: slides.com/kainino/ggr

  • GPUs: Extremely basic hardware architecture
  • ​Graphics:
    • ​Virtual representations of physical space
    • Rasterization and shading
  • Rays: Raycasting, raytracing, and raymarching
    • ​Shiny Shadertoy demos!
      • ​Note: These don't work on iOS right now
  • Lots of borrowed content!
slides.com/kainino/ggr

Shadertoy Teaser

"Snail"

by iq (Inigo Quilez)

(not a video - this is rendering live in the web browser!)

GPUs

slides.com/kainino/ggr

GPU Hardware

  • A GPU is a chunk of silicon designed for 3D rendering
  • Modern GPUs are generalized parallel computing chips
    • But still retain lots of graphics-specialized subsystems
  • Extremely complicated; I won't pretend to know details
slides.com/kainino/ggr

Discrete

  • Separate silicon chip from the CPU
  • Has its own board, RAM, fans, etc.
  • Communicates with the CPU over a hardware bus
    • In a desktop PC, slots into the PC motherboard via PCIe

Integrated

  • A chunk of silicon inside a CPU die or SoC (system-on-a-chip)
  • Usually uses system RAM
  • Found in every phone
    and laptop (some laptops
    also have discrete GPUs)

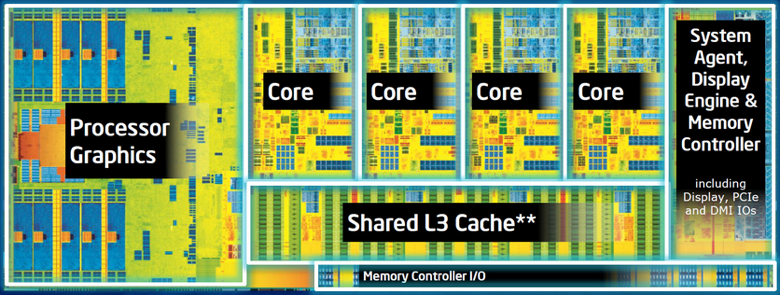
from nvidia.com   from intel.com

slides.com/kainino/ggr

CPU Hardware

  • A CPU is a chunk of silicon designed for doing all sorts of things
    • Operating systems, applications, computations
  • Also incredibly complicated

from intel.com

slides.com/kainino/ggr

CPU vs. GPU

  • GPUs have a gazillion "cores" or "threads":
    • NVIDIA GTX 1080: 2560 "single-precision CUDA Cores"
    • AMD RX 5700 XT: 2560 "Stream Processors"
    • Intel Iris Pro 580: 72 "Execution Units"
    • Qualcomm Adreno 640: 2 "Cores" x 384 "ALUs"
    • ...
  • Compare this with a CPU: Intel i9-9900K: "8 Cores, 16 Threads"
slides.com/kainino/ggr

CPU vs. GPU

  • CPU ≠ GPU: Completely different architectures
  • GPU: Good at parallel arithmetic and parallel memory access
    • Spends most silicon budget on more parallelism!
  • CPU: Good at branches, functions, loops, random memory access
    • Spends silicon budget on better branch prediction, speculative execution, instruction re-ordering, pipelining, smarter/bigger caches (for lower latency memory access)...
slides.com/kainino/ggr

GPUs as specialized computing devices

  • Lots of "fixed-function" hardware to perform graphics-specific tasks:
    • Fetching vertex data from memory
    • Fetching vertex data from memory and smoothing/interpolating it
    • Assembling primitives (quads, triangles, lines)
    • Rasterizing primitives (triangles, lines, points)
    • Maybe some kind of hardware for raytracing (e.g. in NVIDIA RTX)
  • And sometimes specialized hardware for non-graphics:
    • E.g. NVIDIA Volta "Tensor Cores" for machine learning
  • Will be thoroughly ignored by this presentation
slides.com/kainino/ggr

GPUs as general computing devices

  • Also lots of hardware for doing arithmetic and memory access
    • Hundreds or thousands in parallel!
slides.com/kainino/ggr

GPUs as general computing devices

NVIDIA GPU ≠ AMD GPU ≠ Intel GPU ≠ Qualcomm GPU ≠ ARM GPU ≠ Imagination GPU ≠ ...

 

Still very different architectures despite commonalities

slides.com/kainino/ggr

GPUs as general computing devices

  • We can pretend they're comparable on theoretical (or benchmarked) FLOPS
    • fp32 FLOPS: 32-bit floating-point operations per second
      • GFLOPS = Giga FLOPS
    • That's the number of elementary operations the hardware can do on 32-bit single-precision floating point numbers (e.g. x + y or x * y)
      • Note typically a hardware unit can do one add and one mul per cycle
slides.com/kainino/ggr

GPUs as general computing devices

  • What are the theoretical fp32 maximums?
    • NVIDIA GTX 1080: 8873 GFLOPS
      2560 single-precision SIMD (mul+add) "CUDA Cores" @ 1733 MHz (boost)
    • AMD RX 5700 XT: 9754 GFLOPS
      2560 single-precision SIMD (mul+add) "Stream Processors" @ 1905 MHz (boost)
    • Intel Iris Pro 580: 1152 GFLOPS
      576 single-precision SIMD (mul+add) units @ 1000 MHz (boost)
    • Qualcomm Adreno 640: 899 GFLOPS
      768 single-precision SIMD (mul+add) units (I think) @ 585 MHz
  • ​Intel i9-9900K: too different to compare, but can look at
    the highest benchmark measurement 550 GFLOPS     
slides.com/kainino/ggr

GPUs as general computing devices

  • Note: FLOPS does not translate directly into performance!
  • Most workloads are bound by something else
    • Memory access! or graphics-specific processing, etc.
slides.com/kainino/ggr

Hierarchical architecture (NVIDIA Pascal)

1 per GPU

Few per GPU

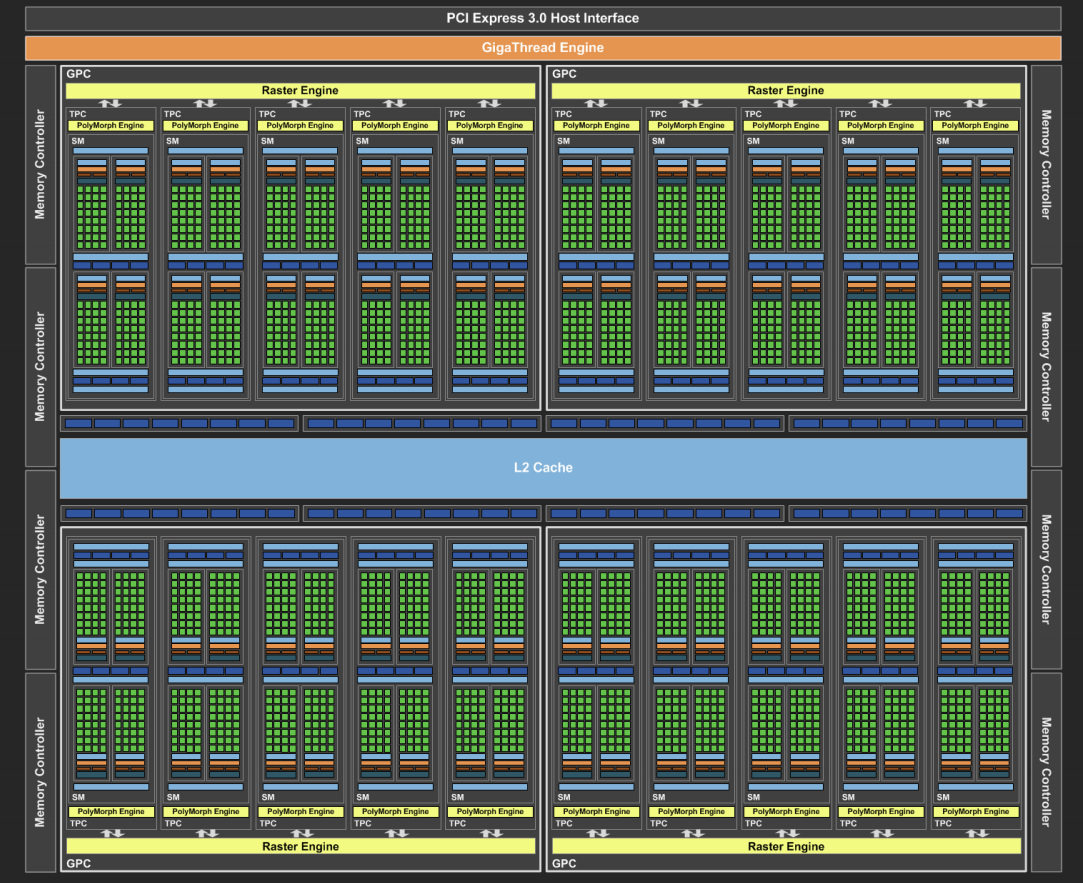
Graphics Processing Cluster

Streaming Multiprocessor

slides.com/kainino/ggr

Hierarchical architecture
(NVIDIA Pascal)

Streaming Multiprocessor

1 per SM

Few per SM

slides.com/kainino/ggr

Hierarchical architecture

slides.com/kainino/ggr

Programming for GPUs

  • CPU parallelism: N separate big cores running in parallel
    • Just create a few OS threads and go
    • (Each core also has SIMD units for data-parallel work)
  • GPU parallelism: N small SIMD cores running 16~64 threads in lock-step
    • Each thread has to be doing approximately the same thing!
    • NVIDIA calls their version "SIMT"
slides.com/kainino/ggr

SIMD (Single-Instruction, Multiple-Data)

  • Executes a single instruction (e.g. ADD) on multiple pieces of data at once:
    • SIMD_ADD [a0, a1, a2, a3], [b0, b1, b2, b3] -> [a0+b0, a1+b1, a2+b2, a3+b3]
    • 4x speed (FLOP/instruction) in this example!
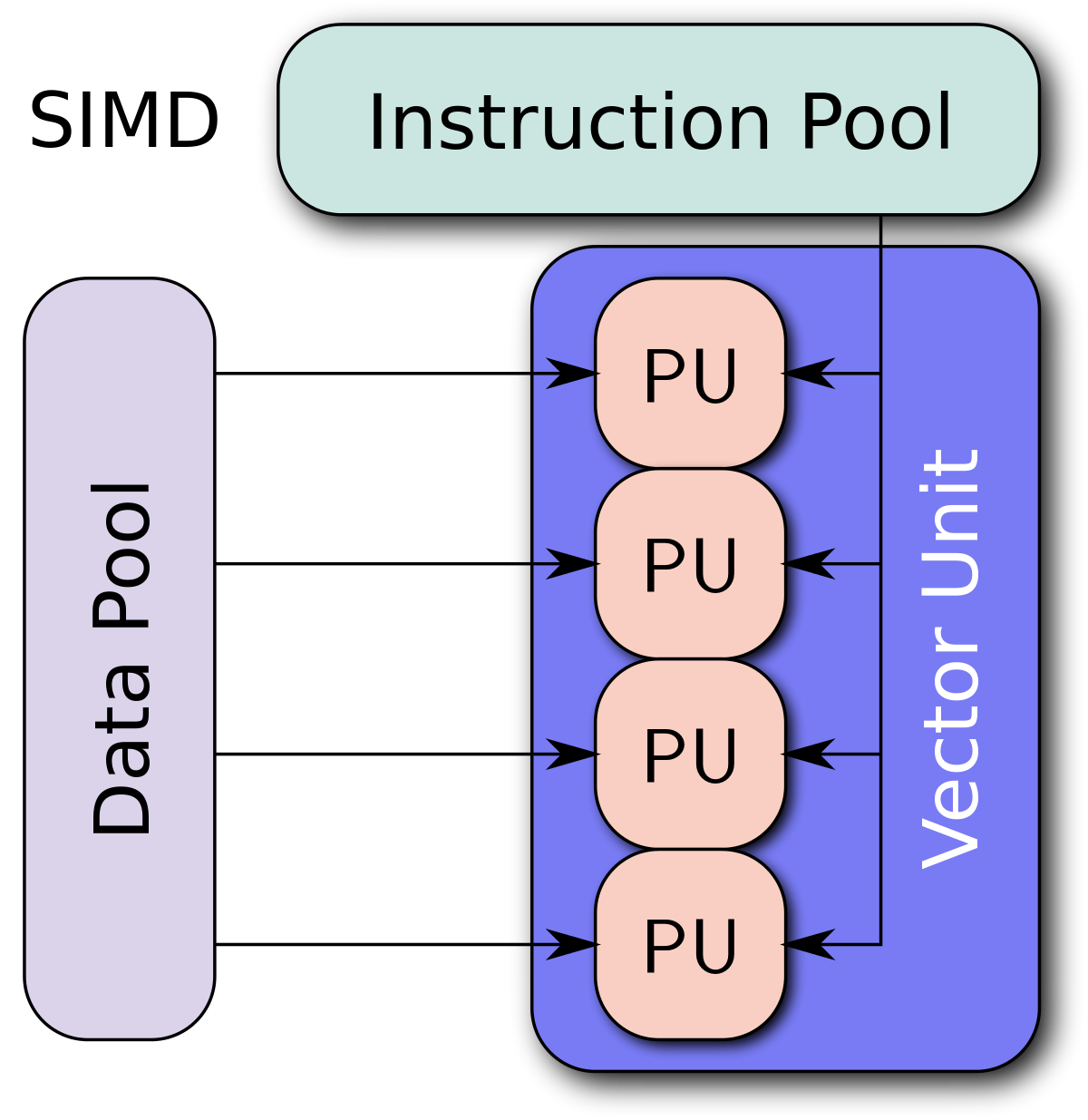
slides.com/kainino/ggr

SIMT (Single-Instruction, Multiple-Thread)

  • Maintain a separate thread state for each SIMD lane
  • Use one SIMD instruction to run the arithmetic for multiple threads
  • Something like this is used by most GPU architectures (but details vary)

from nvidia.com

All SIMD lanes are still operating here, but
the result is just discarded
("wasted" computation)

slides.com/kainino/ggr

GPU architecture and Graphics

  • GPUs are designed this way because it works well for graphics workloads
    • Lots of triangles (Stanford dragon: ~725k triangles)
    • Lots of pixels (2560x1440: 3,686,400 pixels)
  • Each vertex shader thread or fragment shader thread runs in parallel
    • Each point can be positioned on the screen independently
    • Each pixel can compute its color value independently

Computer Graphics

slides.com/kainino/ggr

Computer Graphics

"studies methods for digitally synthesizing and manipulating visual content"

(Wikipedia)

slides.com/kainino/ggr

3D Computer Graphics

That, but 3D

slides.com/kainino/ggr

Problem: How do we represent reality with numbers?

slides.com/kainino/ggr

Representing physical space

  • A point in 3D physical space can be represented as a 3-vector:

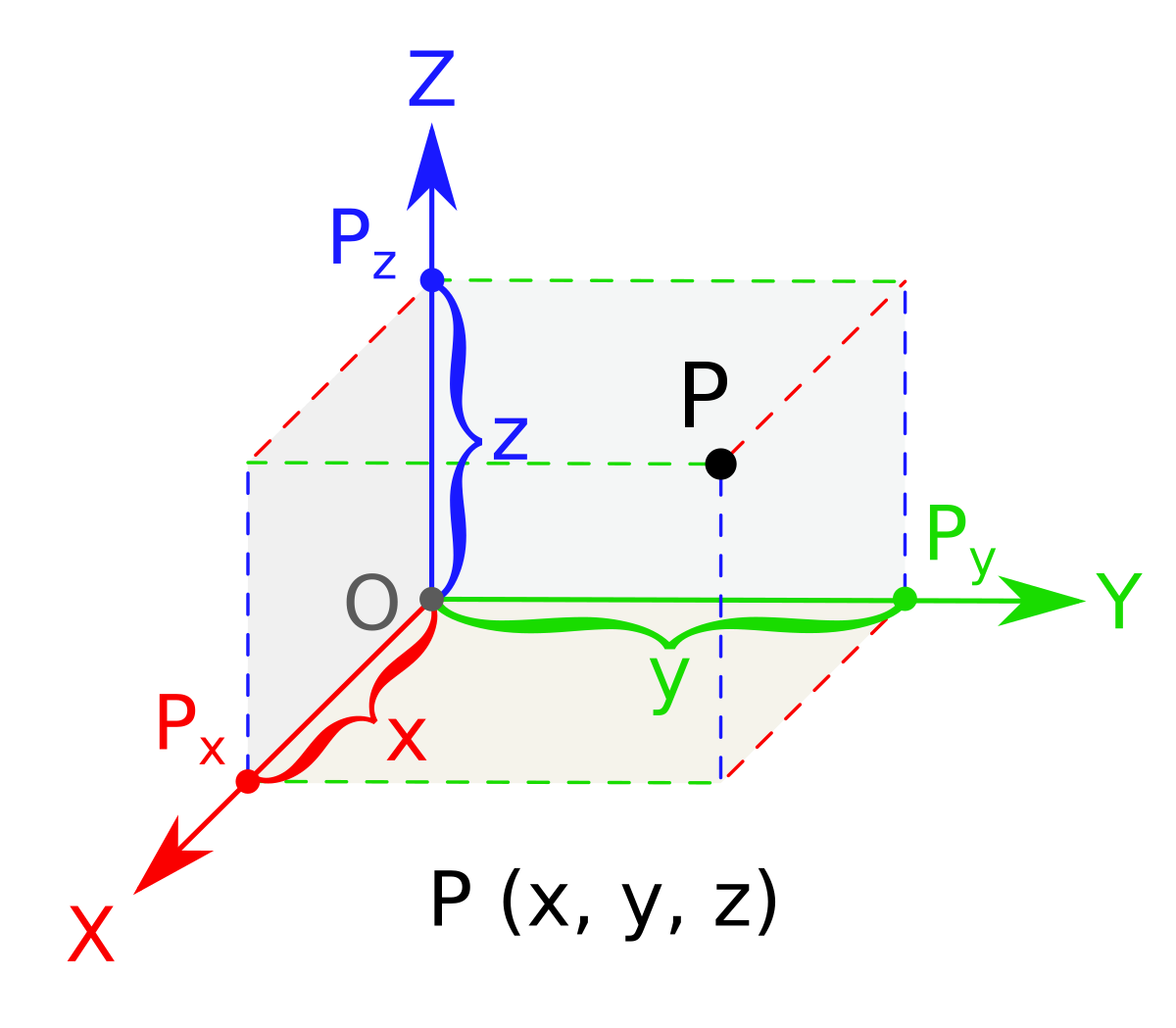
from wikipedia.org

\langle p_x, p_y, p_z \rangle
slides.com/kainino/ggr

Representing physical space

  • A line segment (or line or ray) is represented by 2 points




     
    • (or by a point and a direction)

from wikipedia.org

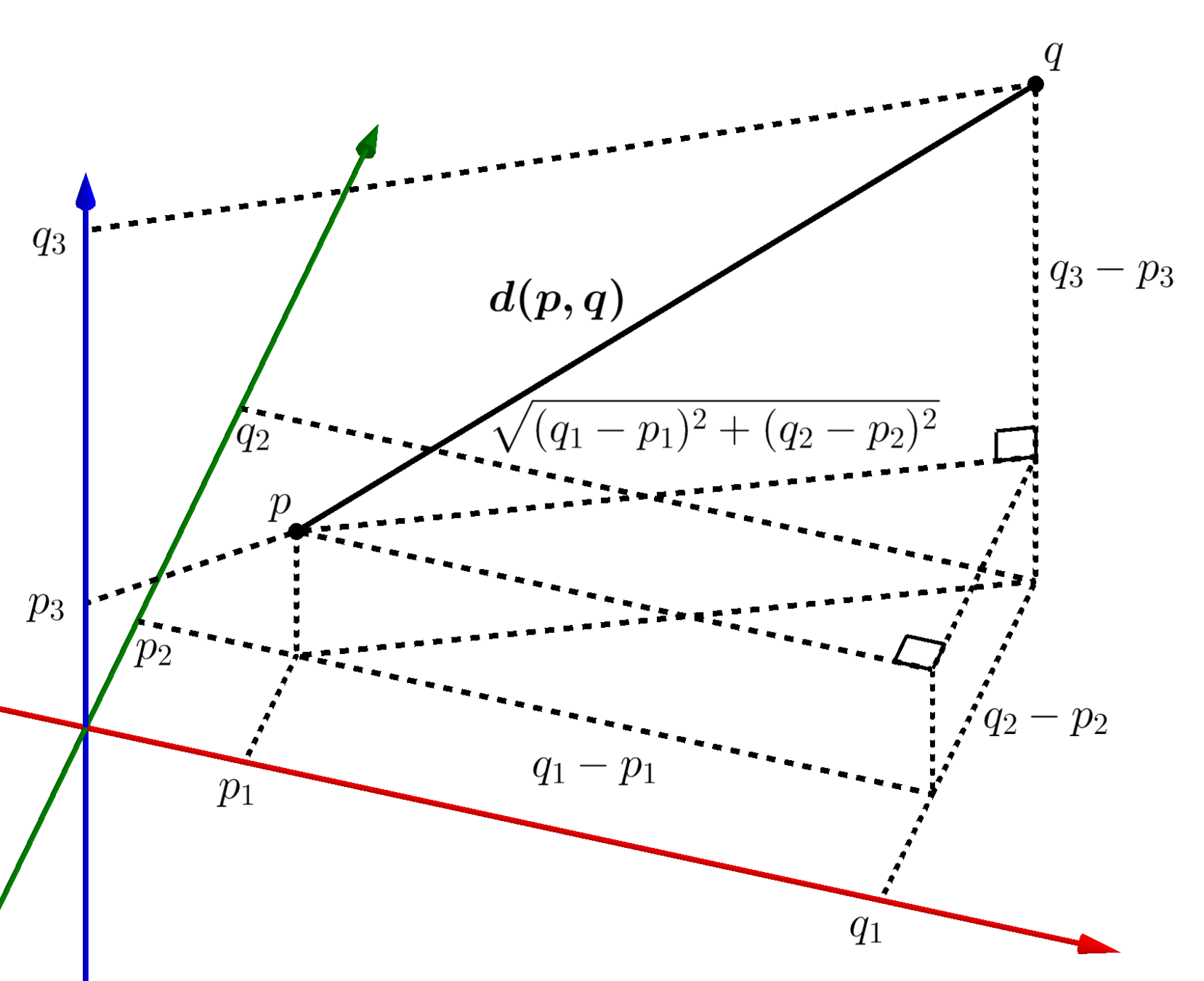
\mathbf p = \langle p_x, p_y, p_z \rangle \\ \mathbf q = \langle q_x, q_y, q_z \rangle
\mathbf p = \langle p_x, p_y, p_z \rangle \\ \mathbf d = \mathbf q - \mathbf p = \langle d_x, d_y, d_z \rangle
slides.com/kainino/ggr

Representing physical space

  • A triangle is represented with 3 points
slides.com/kainino/ggr

Problem: How do we represent real shapes?

slides.com/kainino/ggr

Mesh representation

  • A bunch of triangles together can make a solid object

from wikipedia.org

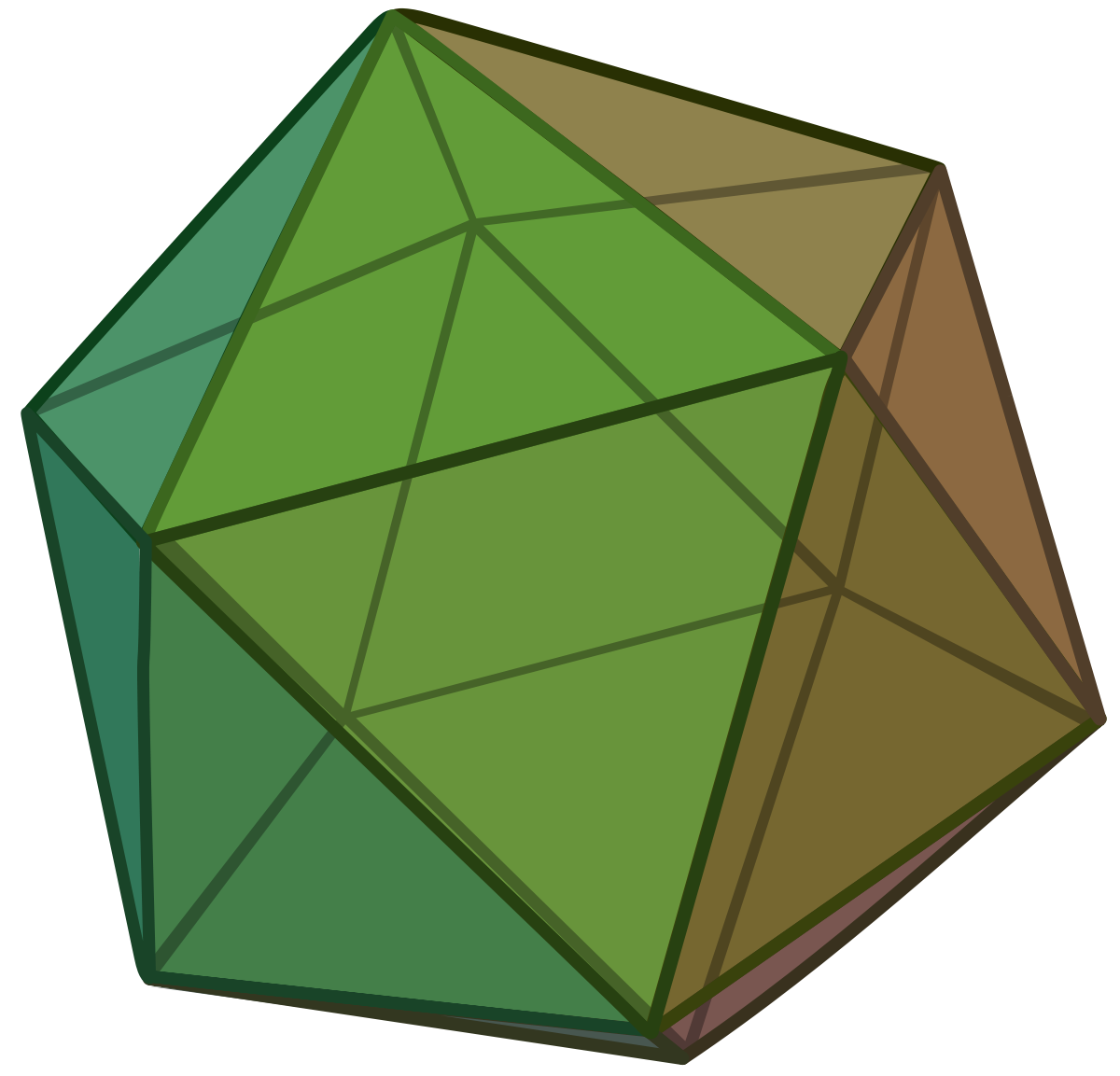
slides.com/kainino/ggr

Mesh representation

  • Real life objects aren't made of triangles...
    • But we can approximate the shape if we use enough triangles

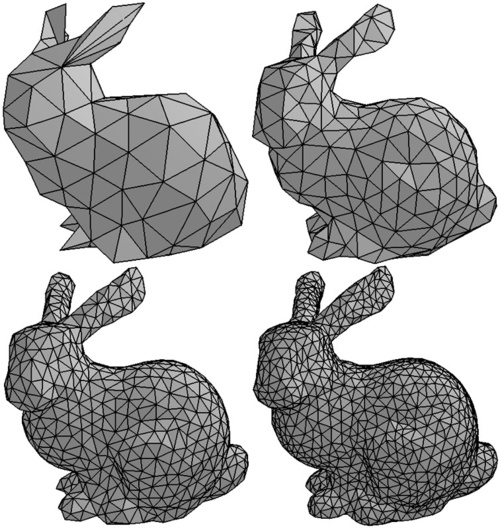
from CMU 15294

slides.com/kainino/ggr

But how do we turn meshes into images?

slides.com/kainino/ggr

Problem: Screens are 2D

  • And eyes see a 2D image
  • So we need to flatten that 3D data to view it
slides.com/kainino/ggr

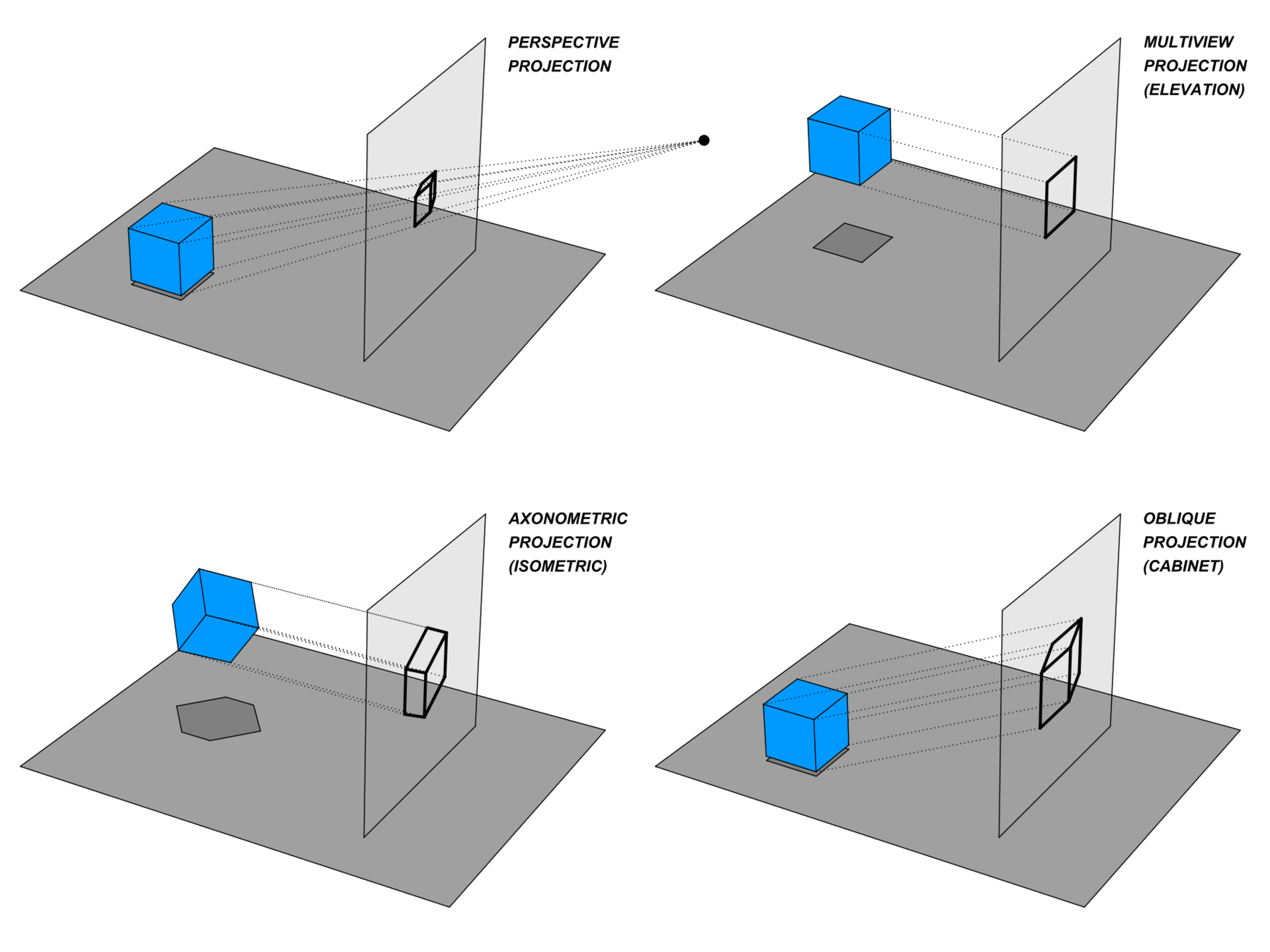
Projection

  • Mapping 3D vectors onto a 2D plane
  • One way: simply "flatten" in some axis (orthographic)
    • Project each point onto the closest point on a plane

from wikipedia.org

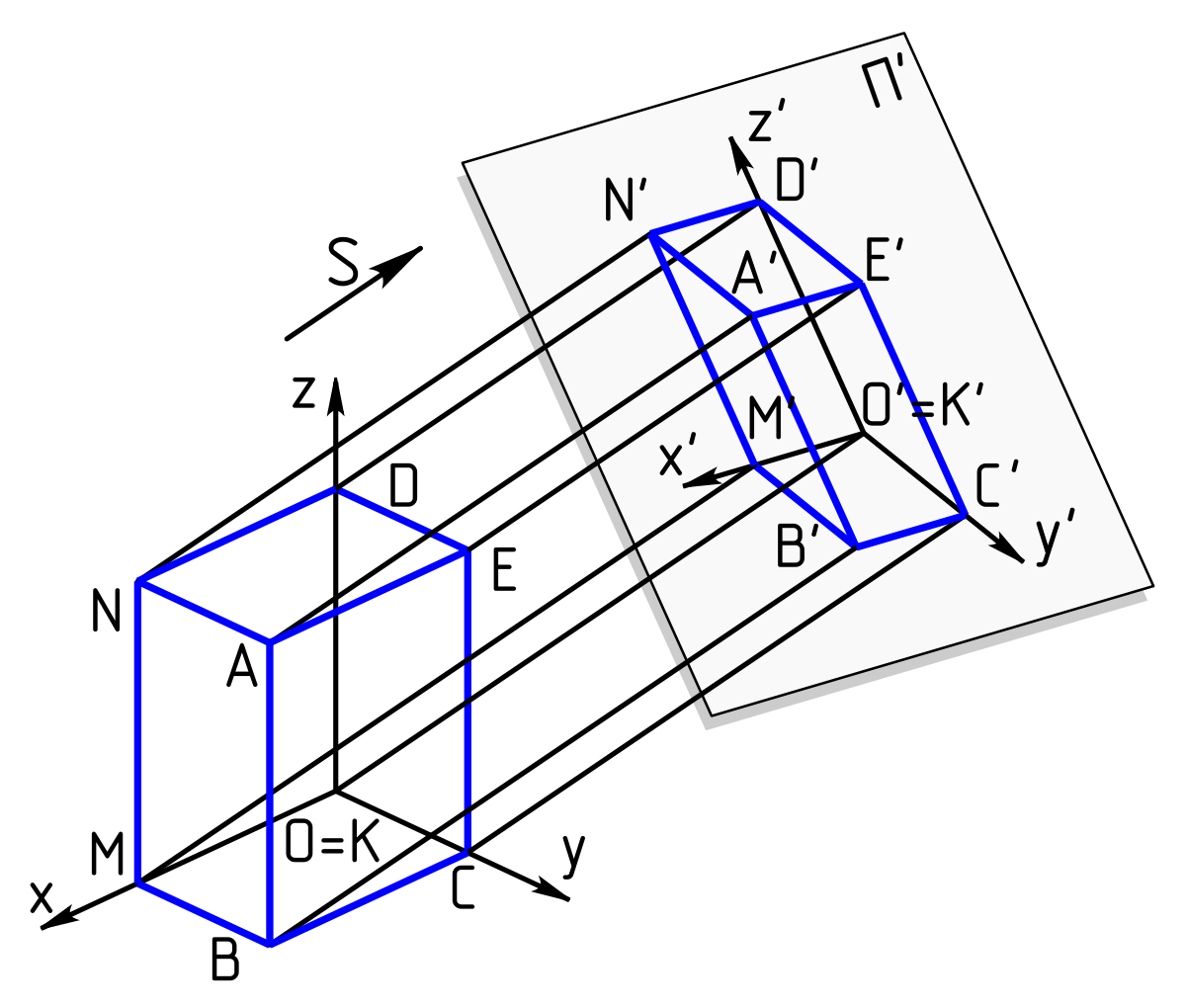
slides.com/kainino/ggr

Projection

  • More physical: perspective projection
  • Project each point along the ray to the "eye"/"camera" location
    • We'll come back to rays....

from wikipedia.org

slides.com/kainino/ggr

Problem: Screens are made of pixels

  • Projection just gives us a bunch of <x, y> points on a plane
    • (and we know how they're connected)
slides.com/kainino/ggr

Rasterization

  • Points are easy...
  • See what pixel it falls in, and fill it in
slides.com/kainino/ggr

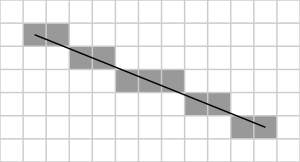
Rasterization

  • Lines are trickier: need to make sure it's always about the right thickness
    • e.g. Bresenham's line algorithm
    • We get to not care: GPU implements this for us (in specialized hardware)!

from wikipedia.org

slides.com/kainino/ggr

Rasterization

  • Triangles: for each line, fill in the space from the left edge to the right edge
    • Scanline-based algorithms
    • GPUs also implement this in hardware
      • Nicely parallelizes (each line is independent)!

from SimmPole on imgur

slides.com/kainino/ggr

... and more

from OpenGL Insights

slides.com/kainino/ggr

OK, so that's complicated

  • And it requires a lot more that I haven't talked about
  • Important: this is how most 3D applications work in practice
    • Computationally efficient
    • Adapts to slow hardware: "just" reduce the number of triangles
  • Let's talk about something less efficient (... but easier)
slides.com/kainino/ggr

Let's backtrack.

slides.com/kainino/ggr

How do we represent real shapes?

  • Meshes are not the only way...
slides.com/kainino/ggr

Analytic representations

  • Some shapes are easy to represent mathematically

Plane

Sphere

Line/ray

\mathbf x = \mathbf o + d \mathbf l ~~~~~~~ d \in \mathbb R
\left( \mathbf p - \mathbf p_0 \right) \cdot \mathbf n = 0
\left\Vert \mathbf x - \mathbf c \right\Vert ^2 = r^2
slides.com/kainino/ggr

Analytic representations

  • And some shapes can be represented by combining other shapes
    • Constructive Solid Geometry

from wikipedia.org

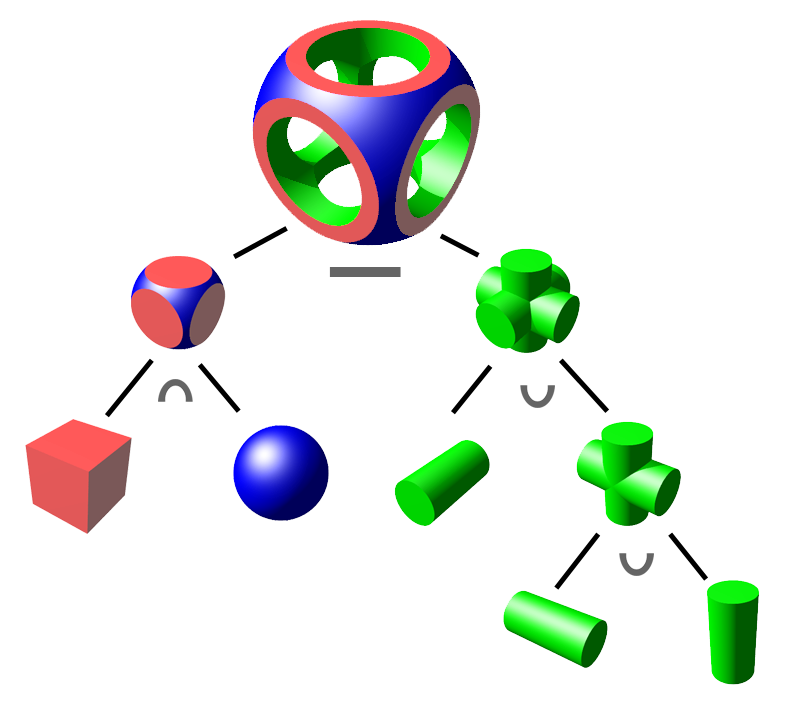
slides.com/kainino/ggr

Signed distance fields (SDF)

  • (Shown in 2D, but same in 3D)
  • At each point in space, defines the distance to the closest point on the surface of the solid
    • Negative "distance" if the point is inside the solid
  • If you trace out the line (2D) or surface (3D) where the SDF is zero, that's the solid!

James Kuffner

slides.com/kainino/ggr

Signed distance fields (SDF)

  • Can compute these mathematically for some shapes

Circle

Triangle

float sdCircle( vec2 p, float r ) {
  return length(p) - r;
}

by Inigo Quilez

slides.com/kainino/ggr

Aside: SDF text

  • 2D SDF is a commonly used representation of text for 3D applications

lambdacube3d.wordpress.com

slides.com/kainino/ggr

But how do we turn those things into images?

slides.com/kainino/ggr

Rays

slides.com/kainino/ggr

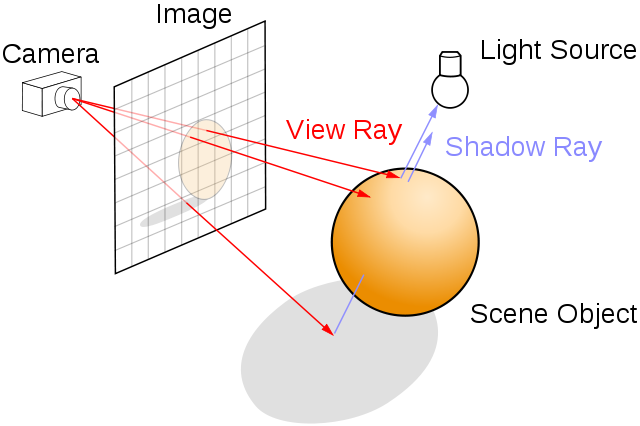
Ray-based rendering

  • From some virtual "camera" position looking at the screen, shoot a ray through each pixel


     
    • l₀: location of the pixel in 3D
    • d: distance along the ray
    • l: direction of the ray = ||l₀ - c||
    • c: location of the camera in 3D
    • x(d): point on the ray
\mathbf x(d) = \mathbf{l_0} + d \mathbf l ~~~~~~~~ d \ge 0
slides.com/kainino/ggr

Raytracing

  • Check for intersections between the ray and the objects in the scene
slides.com/kainino/ggr

Raytracing analytic shapes

  • With analytic representations, ray intersections can be done... analytically!
    • Solve for d, the distance from the screen

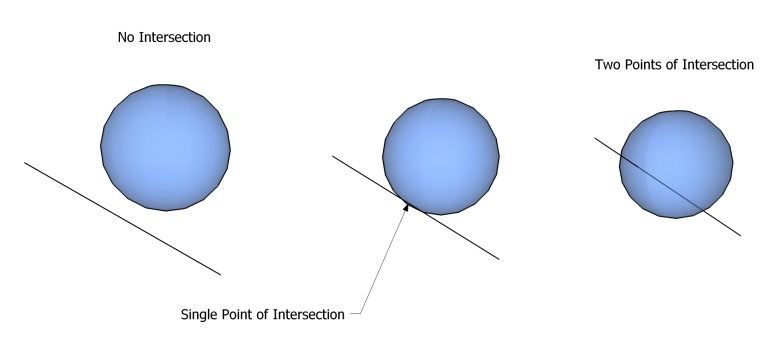
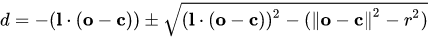
Plane

Sphere

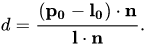
from wikipedia.org

slides.com/kainino/ggr

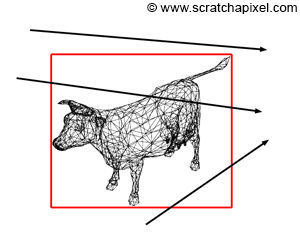
Raytracing meshes

  • Meshes (made of triangles) can also be analytic:
    • Just represent every triangle as a little section of a plane :)
  • But that's a lot of triangles.
    • Have to test ~million rays against ~million triangles
    • Requires tons of work to make it fast enough (spatial acceleration data structures)
slides.com/kainino/ggr

Raytracing some basic objects

^ Go here for code

slides.com/kainino/ggr

Raytracing a plane

float distToPlane( in vec3 pointInPlane, in vec3 planeNormal, in vec3 ro, in vec3 rd ) {
    float divisor = dot(rd, planeNormal);
    
    if (abs(divisor) < 0.001) { // Ray is approximately parallel to the plane
    	return NO_HIT;
    }
    
    float d = dot(pointInPlane - ro, planeNormal) / divisor;
    // d < 0 means the intersection was behind the camera, so don't count it
    return d < 0.0 ? NO_HIT : d;
}

slides.com/kainino/ggr

Raytracing a sphere

float distToSphere( in vec3 sphereCenter, in float sphereRadius, in vec3 ro, in vec3 rd ) {
    vec3 roRelativeToSphere = ro - sphereCenter;
    float discriminant = pow(dot(rd, roRelativeToSphere), 2.0) -
        (dot(roRelativeToSphere, roRelativeToSphere) - pow(sphereRadius, 2.0));
    
    if (discriminant < 0.0) {  // The ray does not intersect the sphere
        return NO_HIT;
    }
    
    // Math says there are two intersections with the sphere:
    //   (...) +/- sqrt(discriminant)
    // But we are only interested in the closer intersection.
    float d = -dot(rd, roRelativeToSphere) - sqrt(discriminant);
    return d < 0.0 ? NO_HIT : d;
}

slides.com/kainino/ggr

Raytracing all that together

float distToClosestObjectInScene( in vec3 ro, in vec3 rd ) {
    float d = NO_HIT;
    
    d = min(d, distToSphere(/*center*/ vec3(0, 0, 0), /*radius*/ 0.5, ro, rd));
    d = min(d, distToSphere(/*center*/ vec3(1, 0.5, -0.5), /*radius*/ 0.5, ro, rd));
    d = min(d, distToSphere(/*center*/ vec3(-1, 0, -0.5), /*radius*/ 0.5, ro, rd));
    d = min(d, distToPlane(/*pointInPlane*/ vec3(0, -1, 0), /*normal*/ vec3(0, 1, 0), ro, rd));

    return d;
}

vec3 render( in vec3 ro, in vec3 rd ) {
    float d = distToClosestObjectInScene(ro, rd);
    return vec3(d * 0.02);  // Visualize the distance as a color
}

slides.com/kainino/ggr

Raymarching

  • Can be used with any representation where you can ask the question:
    "Is this point inside the object?"
slides.com/kainino/ggr

Raymarching (fixed step)

  • Step along the ray in fixed increments
    • Will eventually slightly overshoot the nearest surface
    • Call that the intersection point?

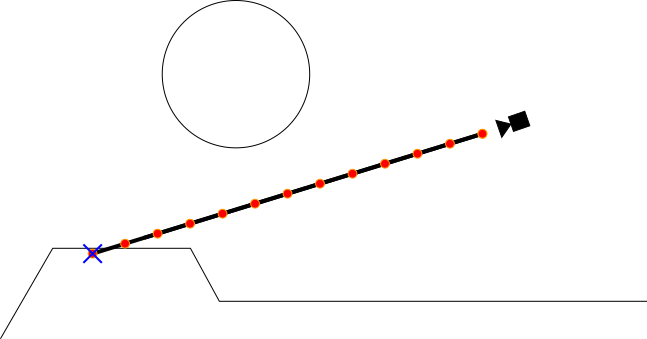
from flafla2.github.io

slides.com/kainino/ggr

Raymarching

  • Takes many steps
    • ​(slow)
  • And can jump past thin objects!
slides.com/kainino/ggr

Sphere tracing

  • Variant on raymarching
  • Fewer steps
    • (less slow)
  • Uses the SDF!
slides.com/kainino/ggr

Sphere tracing

  • Use the SDF to check the distance to the closest surface
  • Jump that distance, knowing your ray can't miss a surface
  • Repeat

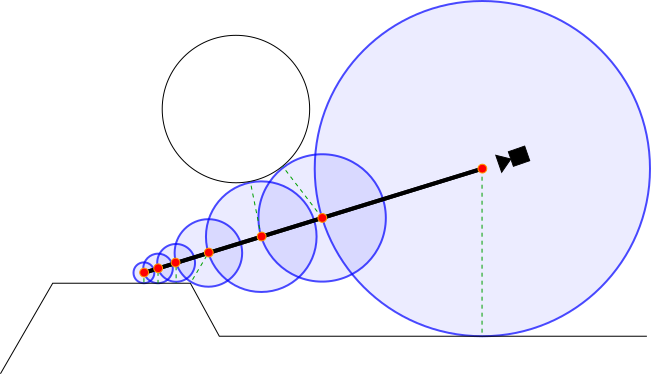
from flafla2.github.io

slides.com/kainino/ggr

Raymarching some basic objects

slides.com/kainino/ggr

Debug view: raymarch step count

slides.com/kainino/ggr

Defining the SDF for the scene

float sdPlane( vec3 probe, vec3 planeScaledNormal ) {
    return (probe - planeScaledNormal).y;
}
float sdSphere( vec3 probe, vec3 sphereCenter, float sphereRadius ){
    return length(probe - sphereCenter) - sphereRadius;
}
float sdUnion(float a, float b){
    return min(a, b);
}
float map( in vec3 pos ){
    float res = 1e10;
    res = sdUnion( res, sdPlane(  pos, vec3( 0.0, -1.0, 0.0) ) );
    res = sdUnion( res, sdSphere( pos, vec3( 0.0,  0.0, 0.0), 0.5 ) );
    res = sdUnion( res, sdSphere( pos, vec3( 1.5,  0.5, -0.5), 0.25 ) );
    return res;
}

slides.com/kainino/ggr

Raymarching the scene with sphere tracing

#define MAX_ITERATIONS 150
float castRay( in vec3 ro, in vec3 rd ) {
    // raymarch primitives
    float distAlongRay = 0.0;
    for( int i=0; i < MAX_ITERATIONS; i++ ) {
        // Probe the SDF map
        float sdValue = map( ro + rd * distAlongRay );
        if( abs(sdValue) < (0.0001 * distAlongRay) )
        {
            return distAlongRay;
        }
        distAlongRay += sdValue;  // <- sphere tracing!
    }
    return -1.0;  // nothing found
}


// (and then we visualize distAlongRay as a color, like before.)
slides.com/kainino/ggr

Raymarching parallelism

  • Each pixel does the same loop, but with a different ray
  • One "SIMT" thread per pixel
  • Same computations on each thread:
    • Loop over:
      • Compute the SDF
      • Check whether to continue
  • In a SIMT group, thread A takes more iterations than thread B...
    • Thread B's lane just goes idle for a bit
slides.com/kainino/ggr

Graphics

(again)

slides.com/kainino/ggr

Materials and lighting lightning talk

  • Super fast intro to materials, lighting, and shading
slides.com/kainino/ggr

Light scattering

  • When light hits a surface, it scatters according to some distribution function
    • Bidirectional scattering distribution function
    • A property of the surface

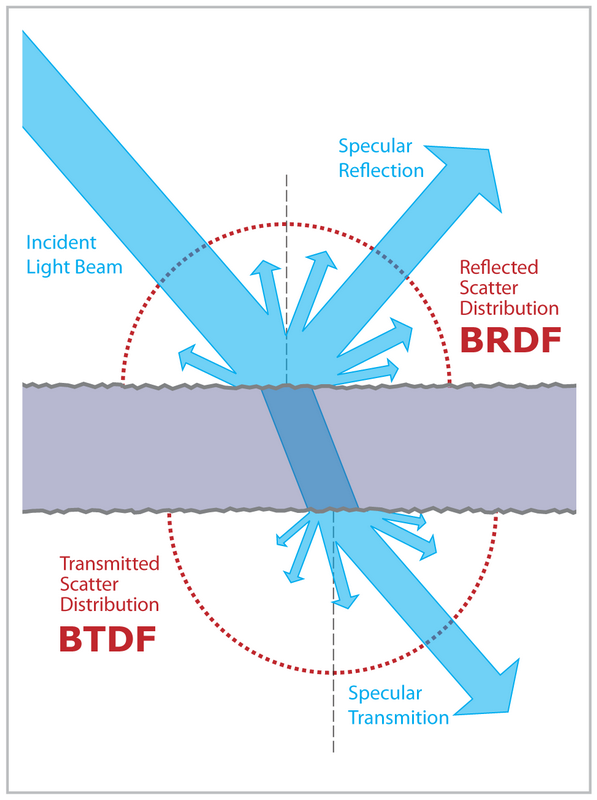
from wikipedia.org

slides.com/kainino/ggr

Diffuse & specular

  • A common (and fast) approximation is that there are just two scattering components
    • Diffuse light that scatters randomly (like clay or wood)
    • Specular light that reflects (like a glaze on ceramic, or a metal)

from wikipedia.org

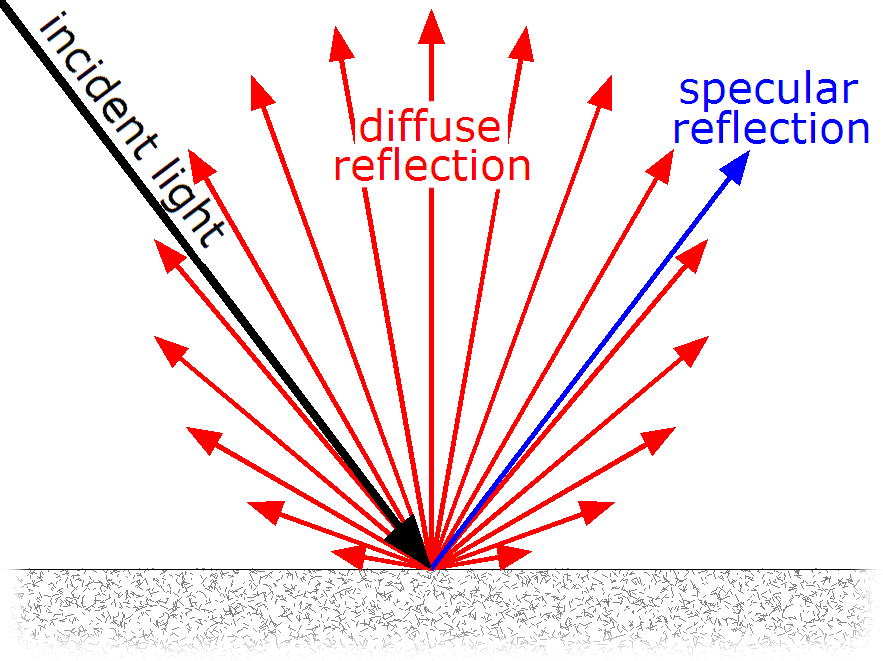
slides.com/kainino/ggr

Refraction

  • Light lenses and bounces around inside transparent materials like glass

from wikipedia.org

slides.com/kainino/ggr

Subsurface scattering

  • Light can also scatter inside a material
    • Like skin, milk, most food

from wikipedia.org

slides.com/kainino/ggr

Shadows

  • Shadows don't occur naturally with these approximations
    • Have to add them in ourselves
    • Tons of ways to do this
slides.com/kainino/ggr

Shadows

  • A point is in shadow if it can't see the light source
    • We can check by just shooting a ray toward the light
    • Gives a yes/no answer
    • Which produces a shadow with a hard edge

from wikipedia.org

slides.com/kainino/ggr

Shadows

  • But in real life, shadows are soft
    • Because light sources aren't infinitely small points

from wikipedia.org

slides.com/kainino/ggr

Shadows

  • Could take the average of multiple rays toward random points on the light source
  • Or multiple rays in random directions!
  • And then keep bouncing until you find a light!
  • This is called pathtracing, and, more than just soft shadows, can fully simulate light bouncing around the entire scene (global illumination) to generate physically correct images

from wikipedia.org

slides.com/kainino/ggr

Shadows with raymarching

  • Recall: when raymarching we see the distance to the closest object at every point along the ray 
slides.com/kainino/ggr

(alternating physically accurate shadows (grainy) with approximated shadows (smooth))

Shadows with raymarching

slides.com/kainino/ggr

Raymarching, lighting, and shadows

Check out iq's Raymarching - Primitives for a nice demo of all of these together

slides.com/kainino/ggr

Combining all that

  • With clever approximations of all of the phenomena we just talked about...
slides.com/kainino/ggr

"Snail"

by iq (Inigo Quilez)

Making of Inigo Quilez's "Snail"

Fun Shadertoy demos

slides.com/kainino/ggr

[SIG15] Mario World 1-1

by knarkowicz

(All video in one shader - and every pixel is completely independent!
Audio is also generated by a shader run on the GPU.)

[SH16C] Contra

... also by knarkowicz

(4 stages + one for audio)

Thanks!

Questions?

Made with Slides.com