week 06

Representation Learning on Graphs

Social Network Analysis

Network Embeddings

Graphs representation

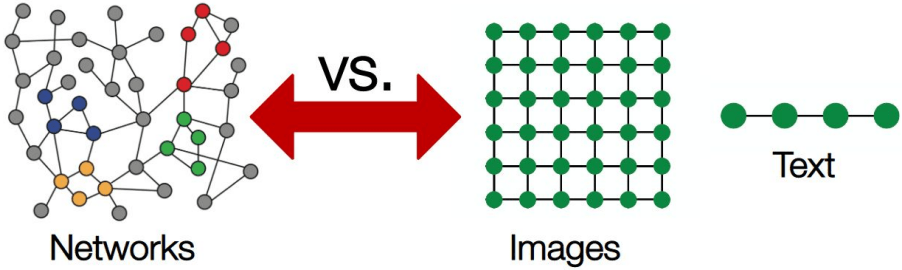
In many fields the data have a graph structure

  • social: friendship graph in social networks, graph of scientific citations
  • man-made: internet, web, road networks, air communication networks
  • In biology: protein interactions, complex molecules.

Graph representation

  • supervised, semi-supervised
    • node classification
      • Is the account a bot
      • Predicting user age, gender, profession in a social network
      • Predicting the function of a new protein based on its interaction with others
      • article topic prediction on the basis of citations
    • link prediction
      • content recommendation in an online platform
      • forecasting drug side effects
    • community detection
      • searching for users with similar interests
      • Revealing functional groups of proteins

Objective: extract features from the graph in a form suitable for machine learning algorithms

Machine learning tasks on graphs and their applications

Approaches to learning graph representations

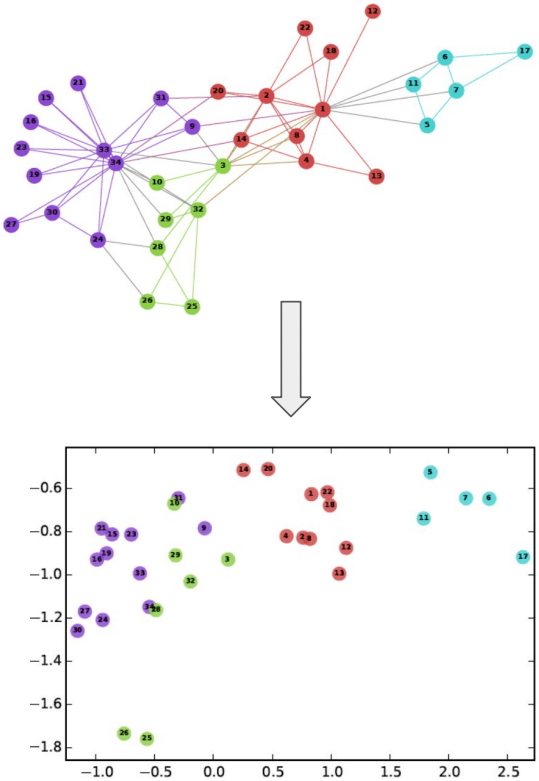
Task: find a representation of graph vertices as vectors of (low-dimensional) space that preserve useful information. Normally, vectors are close in space if the vertices are close in the graph

graph embedding ~ representation learning

Approaches:

  1. Naive methods;
  2. Based on matrix decompositions;
  3. Based on random walks;
  4. Graph neural networks.
  5. Other (edge probability)

Naive Approaches

Simple graph representations

  • Graphlets

  • Centralities

  • Layout Based

Matrix Decomposition

Node representation as a dimensionality reduction problem with information preservation.

General idea: represent the graph as a matrix and decompose it.

SVD example

Notation:

  • \( G(V,E) \) - graph with vertices \( V \) and edges \( E \)
  • \( W \) - adjacency matrix with weights
  • \( D \) - diagonal degree matrix
  • \( L = D - W \) - Laplacian of the graph
  • \( Y_i \) is the vector representation of a vertex \( i \) of dimension \( d \ll |V| \)
  • \( I \) is a unary matrix
  • \( \phi(Y) \) - loss function

≈

d

d

|V|

|V|

\( d \ll|V| \)

Locally Linear Embedding

Y_i \approx \sum_j W_{i j} Y j
\phi(Y)=\sum_i\left\|Y_i-\sum W i j Y j\right\|^2

is reduced to finding the smallest eigenvectors of the sparse matrix \( (I-W)^T(I-W) \)

K. Saul, T. Roweis: An Introduction to Locally Linear Embedding (2000) [pdf]

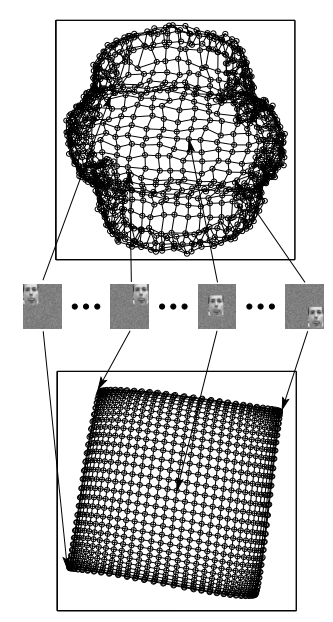
Laplacian Eigenmaps

M. Belkin, P. Niyogi: Laplacian Eigenmaps for Dimensionality Reduction and Data Representation (NIPS, 2002) [pdf]

is reduced to finding the smallest eigenvectors of the normalized Laplassian

Y^T D Y=I

Idea: vertex representation is close if the vertices are connected

\phi(Y)=\frac{1}{2} \sum_{i, j}\left\|Y_i-Y j\right\|_2^2 W_{i j}=\operatorname{Tr}\left(Y^T L Y\right)
L_{n o r m}=D^{-1 / 2} L D^{-1 / 2}

 Cauchy Graph Embeddings

Another distance function \( distance = \frac{|Y_i - Y_j|^2}{|Y_i - Y_j|^2+\sigma^2} \)

\phi(Y)=\frac{1}{2} \sum_{i, j} \frac{W_{i, j}}{\left|Y_i-Y_j\right|^2+\sigma^2}

D. Luo, C. Ding, F. Nie, H. Huang: Cauchy Graph Embedding (ICML 2011) [pdf]

Matrix Decomposition

Naive method problems

The main problem is maintaining only 1st order proximity

Definitions:
First-order proximity between vertices \( i \) and \( j \) = edge weight \( W_{ij} \)
Let  be the \(k\)-order closeness. Then the \( (k+1) \) order closeness between vertices \( i \) and \( j \) = the similarity measure of vectors \( s_i \) and \( s_j \) .

≈

d

d

|V|

|V|

\( d \ll|V| \)

GraRep (CIKM, 2015)

The representations for all k are concatenated. The disadvantage is the complexity of the algorithm \( O(|V|^3) \).

Normalized transition matrix \( X^k_{i,j}=log\frac{A^k_i,j}{\sum\limits_iA^k_{i,j}}-\log\beta \)

\phi(Y)=\left\|X^k-Y_s^k Y_t^{k T}\right\|_F^2

S. Cao, W. Lu, Q. Xu: GraRep (CIKM, 2015) [link]

HOPE

Take S proximity matrix instead of adjacency matrix (Katz Index, Rooted Page Rank, Common Neighbors, Adamic-Adar score)

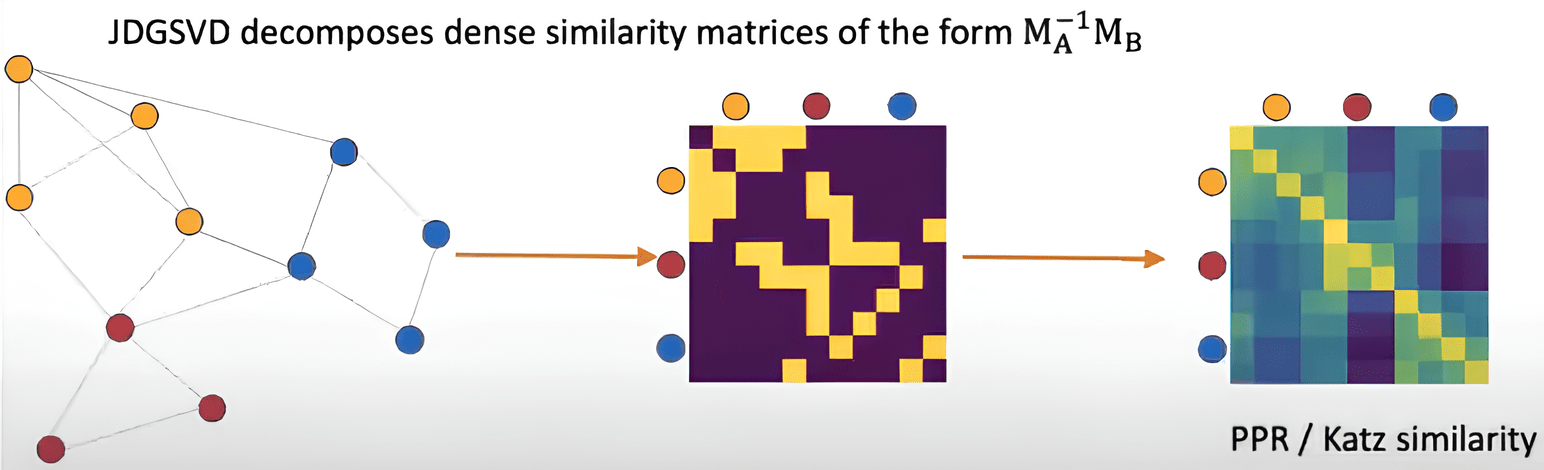
\phi(Y)=\left\|S-Y_s Y_t^T\right\|_F^2, \text { comp. complexity } O\left(|E| d^2\right)\phi(Y)=\left\|X^k-Y_s^k Y_t^{k T}\right\|_F^2

The main disadvantages of matrix decomposition algorithms: only the 1st order closeness and/or high complexity of the algorithm

D. Zhu, et all: High-order Proximity Preserved Embedding For Dynamic Networks , KDD 2016

AROPE

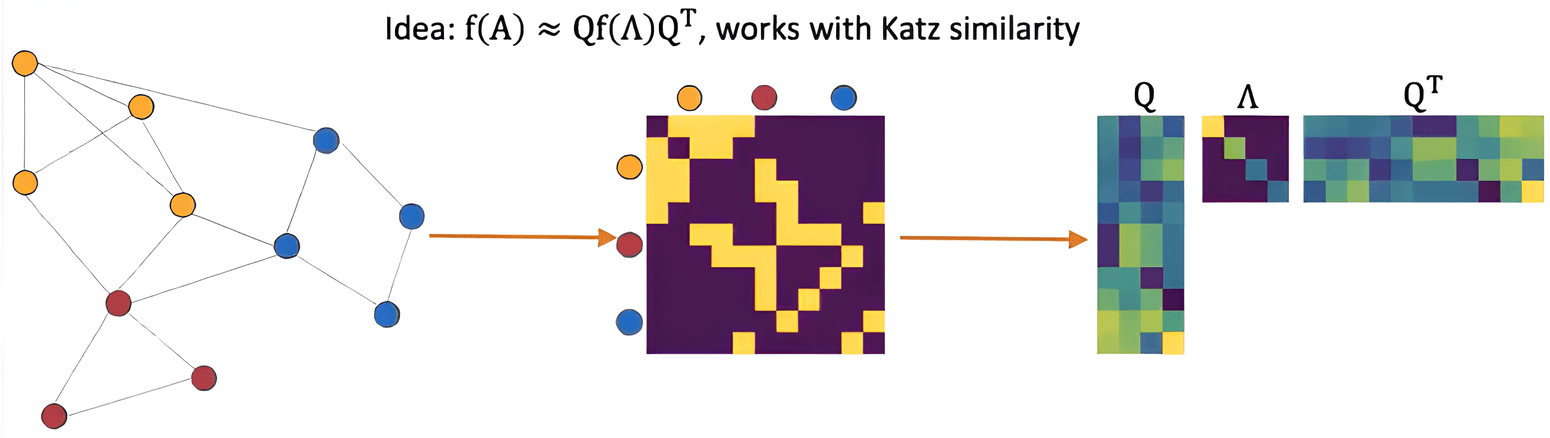
M. Ou, P. Cui, J. Pei, Z. Zhang, W. Zhu: Asymmetric Transitivity Preserving Graph Embedding [pdf]

authors’ code (MATLAB) [link]

Z. Zhang, P. Cui, X. Wang, J. Pei, X. Yao, W. Zhu: Arbitrary-Order Proximity Preserved Network Embedding [pdf]

authors’ code (MATLAB + Python) [link]

HOPE

AROPE

Random Walk

Word2vec

 

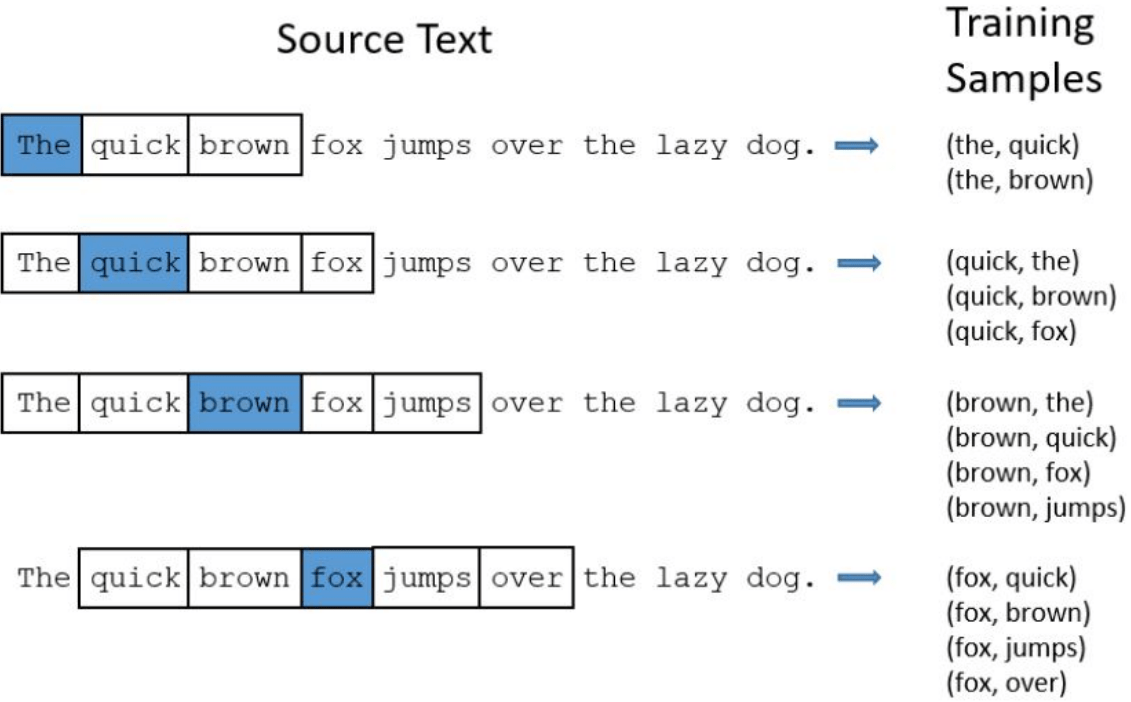
word2vec learns vector representations of words, useful in application tasks. Vectors show interesting semantic properties. For example:

  • king: male = queen: female ⇒
  • king - man + woman = queen

Word2vec

 

word2vec explanation

 

word2vec seminar

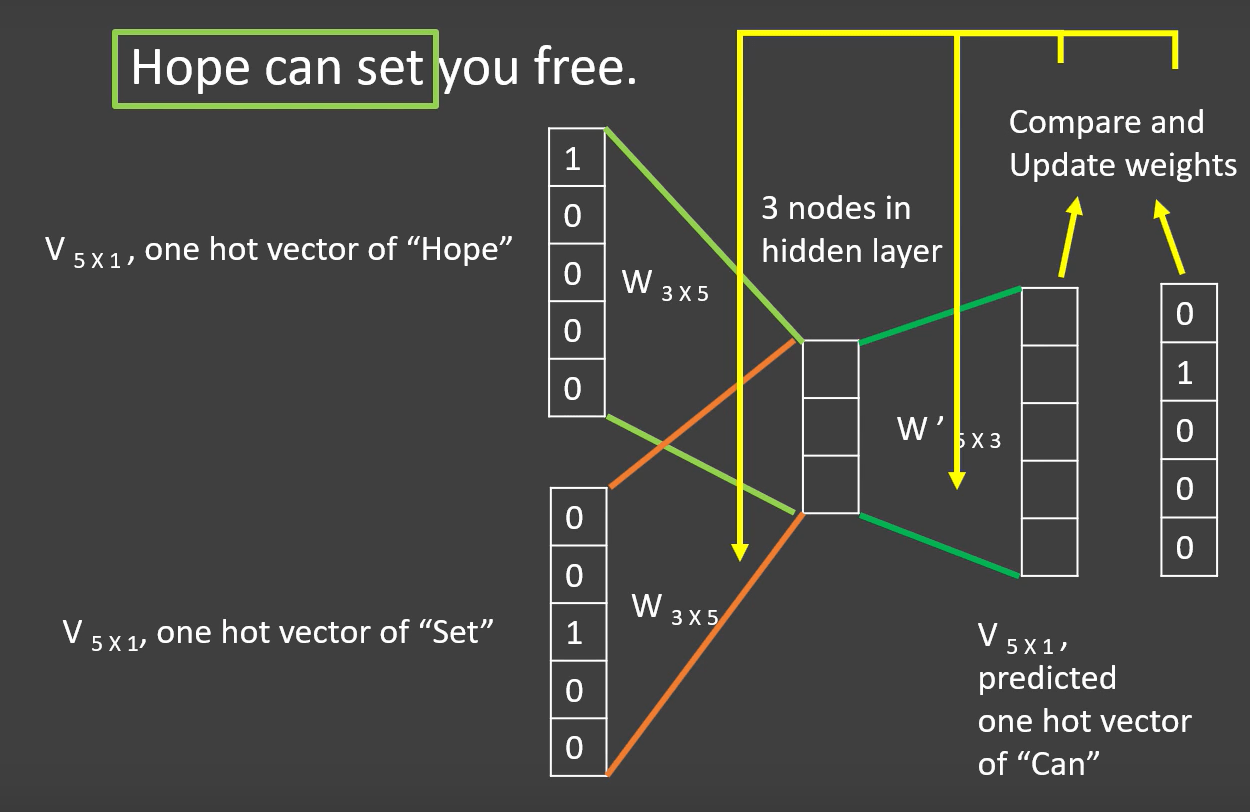
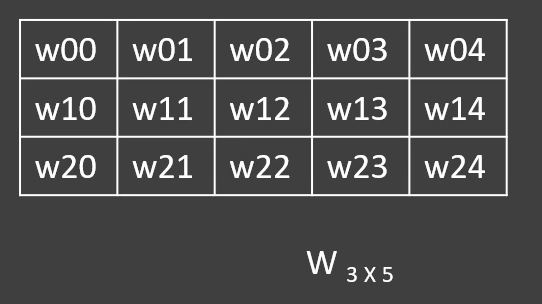
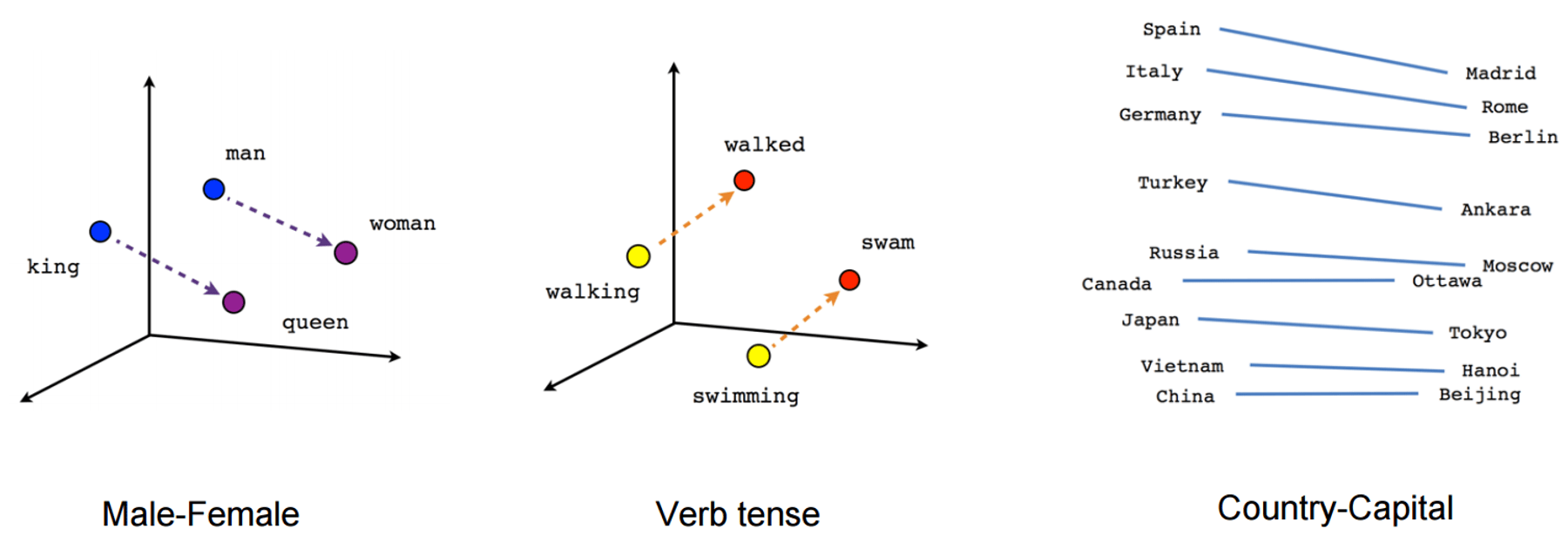
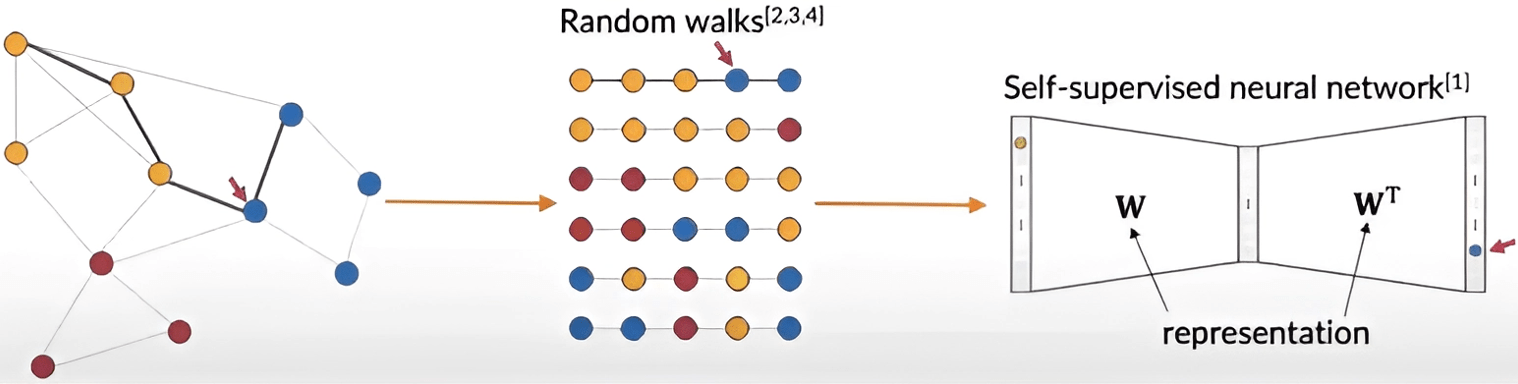
Random walks

 

Key Idea: Nodes in random walks \( \approx \) words in  sentences -> use word2vec.

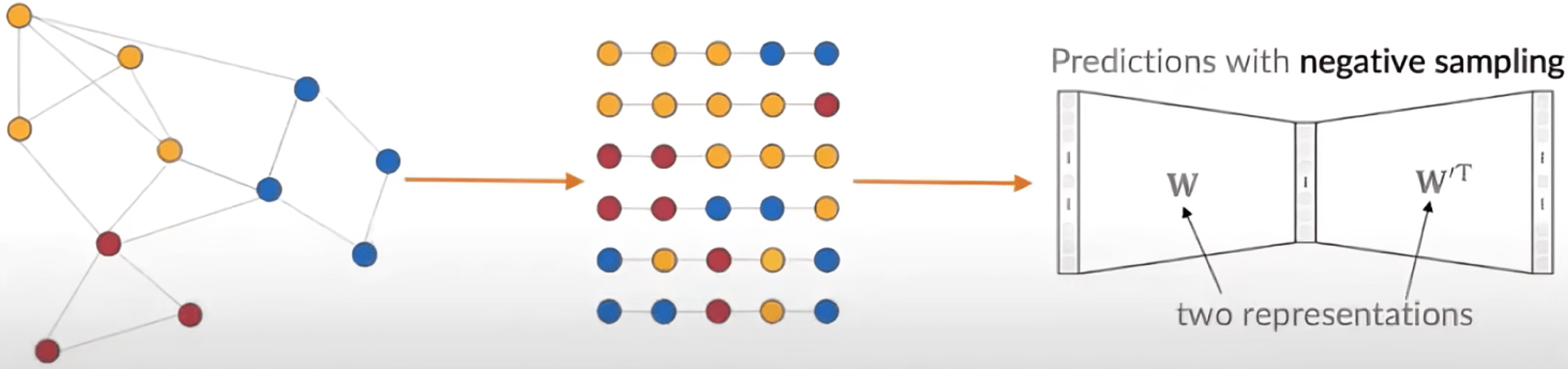
Deepwalk

 

  • Parameters
    • In practical tasks \( w = 10 \), \( \gamma=80 \), \( t=80 \)
    • newer change \( w \)
    • If you lower \( w \), increase \( \gamma \), \( t \)

 

B. Perozzi, R. Al-Rfou, S. Skiena: DeepWalk: Online Learning of Social Representations​ (KDD, 2014) [pdf]

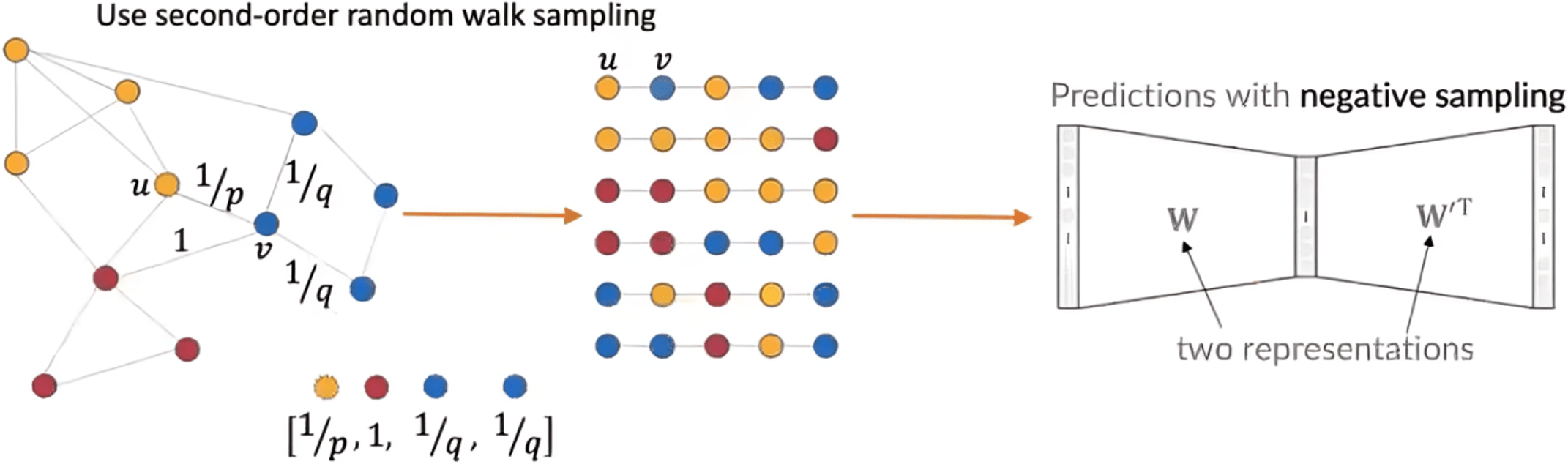
authors’ code (Python) [link], C++ code [link]

Node2vec

 

Low q - explore intra-cluster information
High q - explore inter-cluster information

A. Grover, J. Leskovec: Scalable Feature Learning for Networks [pdf], authors’ code (Python) [link] C++ code [link]

Large-scale Information Network Embedding (LINE)

Key Idea: - don't generate random walks

J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, Q. Mei: LINE: Large-scale Information Network Embedding, WWW, 2015 [pdf]

code (C++) [link]

p_1(v_i, v_j ) = \dfrac{1}{1 + \exp(−u^T_i u_j)}
p_2(v_i| v_j ) = \dfrac{\exp(−u^{'T}_i u_j)}{\sum^{|V|}_{k=1}\exp(−u^{'T}_k u_i)}
O_1 = - \sum_{(i,j) \in E} w_{ij} \log{p_1(v_i,v_j)}
O_2 = - \sum_{(i,j) \in E} w_{ij} \log{p_2(v_i|v_j)}
\hat{p_1}(i, j ) = \dfrac{w_{ij}}{\sum_{(i,j)\in E^{w_ij}}}
\hat{p_1}(v_j| v_i ) = \dfrac{w_{ij}}{d_i}
d_i = \sum_{k \in N(i)}w_{ik}

VERSE

A. Tsitsulin, D. Mottin, P. Karras, E. Müller: Versatile Graph Embeddings from Similarity Measures, WWW, 2018 [pdf], authors’ code (C++) [link]

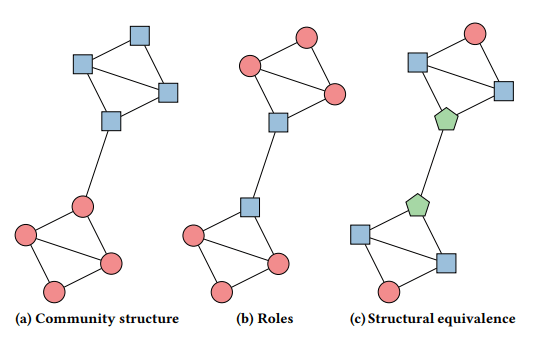
Useful Links

 

I. Makarov​, D. Kiselev​1, N. Nikitinsky, L. Subelj: Survey on graph embeddings and their applications to machine learning problems on graphs [link]

J. Qiu, Y. Dong, H. Ma, J. Li, K. Wang, J. Tang: Unifying DeepWalk, LINE, PTE, and node2vec [pdf]

authors’ code (Python) [link]

  • NetMF

Z. Zhang, P. Cui, H. Li, X. Wang, W. Zhu: Billion-scale Network Embedding with Iterative Random Projection [pdf]

 

authors’ code (Python) [link]

  • RandNE

H. Chen, S. Fahad Sultan, Y. Tian, M. Chen, S. Skiena: Fast and Accurate Network Embeddings via Very Sparse Random Projection [pdf]


authors’ code (Python) [link]

  • FastRP

D. Yang, P. Rosso1, B. Li and P. Cudre-Mauroux: Highly Efficient Graph Embeddings via Recursive Sketching [pdf]

 

authors’ code (C++ & Python) [link]

  • NodeSketch
Made with Slides.com