week 05

Network Models

Social Network Analysis

Network Models

Empirical network features:

Power-law (heavy-tailed) degree distribution
Small average distance (graph diameter)
Large clustering coefficient (transitivity)

Generative models:

Random graph model (Erdos & Renyi, 1959)
Preferential attachment model (Barabasi & Albert, 1999)
Small world model (Watts & Strogatz, 1998)

04-1

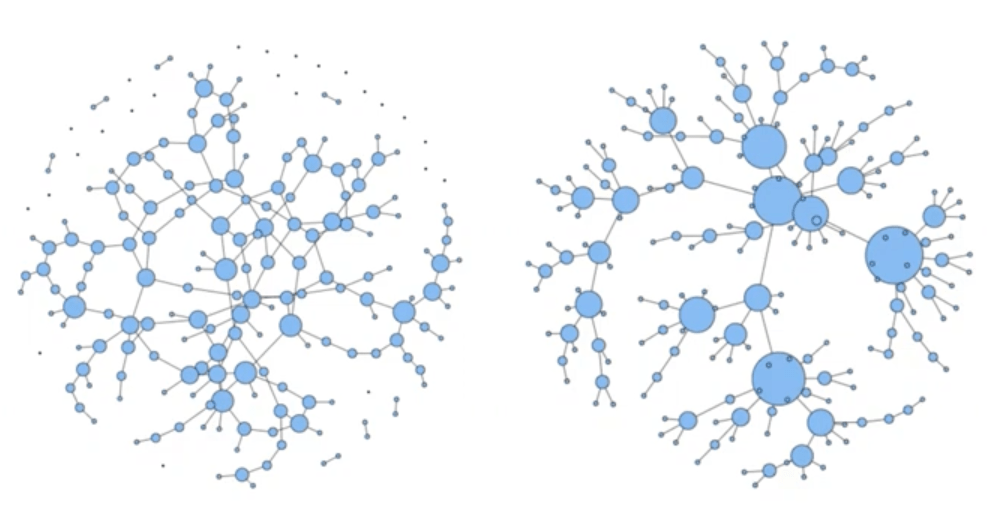
Prefferential Attachment

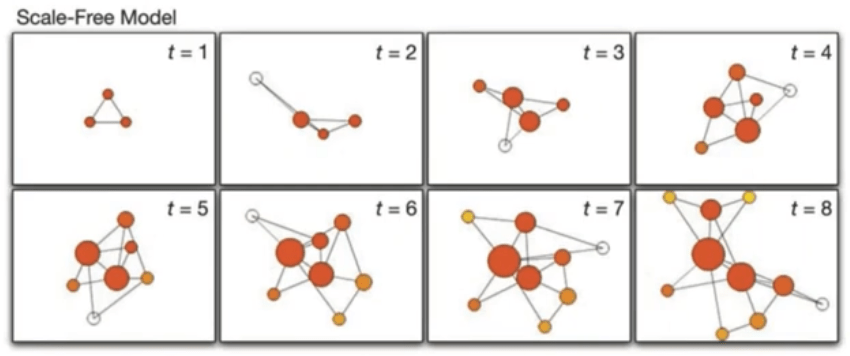
Preferential attachment model

Barabasi and Albert, 1999
Dynamic growth: start at \( t \) = 0 with по nodes and \( m_0 \geq n_0 \) edges

At each time step add a new node with \( m \) edges \( (m \leq n_0) \),
connecting to \( m \) nodes already in netwrok \( k_i(i) = m \)

The probability of linking to existing node i is proportional to
the node degree \( k_i \)

after \( t \) timesteps: \( t + n_0 \) nodes, \( mt + m_0 \) edges

1. Growth

2. Preferential attachment

П(k_i) = \frac{k_i}{\sum_ik_i}

Preferential attachment model

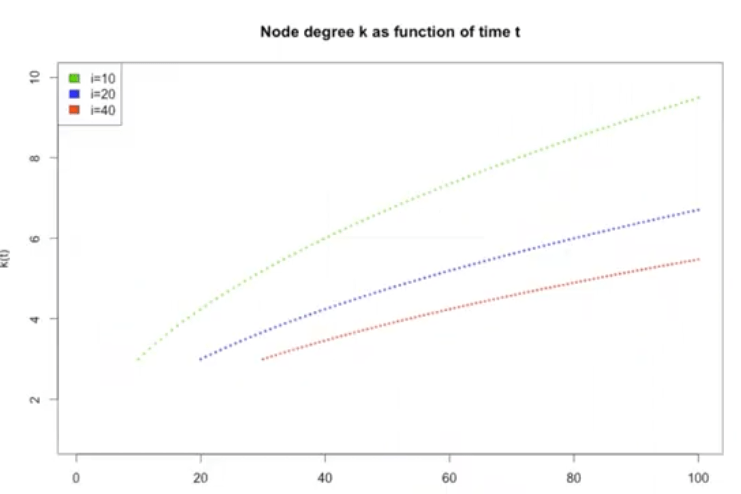
Continues approximation: continues time, real variable node degree \( \langle k_j(t) \rangle \) - expected value over multiple realizations

node \( i \) is added at time \( t_i \) : \( k_i (t_i) = m \)

Solution:

\frac{dk_i(t)}{dt} = m П(k_i) = m \frac{k_i}{\sum_ik_i}=\frac{mk_i}{2mt}=\frac{k_i}{2t}

k_i(t + \delta t) = k_i(t) + m П(k_i)\delta t

\int_m^{k_i(t)} \frac{dk_i}{k_i} = \int_{t_i}^t \frac{dt}{2t}

k_i(t) = m ( \frac{t}{t_i})^{1/2}

Preferential attachment model

k_i(t) = m ( \frac{t}{t_i})^{1/2}

\frac{d k_i(t)}{dt} = \frac{m}{2}\frac{1}{\sqrt{tt_i})}

Preferential attachment model

Time evolution of a node degree

Cumulative function:

Distribution function:

m \Bigl ( \frac{t}{t_i} \Bigr )^{1/2} \leq k

P(k) = \frac{d F(k)}{dk} = \frac {2m^2}{k^3}

F(k) = P(k' \leq k) = \frac{n_0 + t - m^2t/k^2}{n_0 + t} \approx 1 - \frac{m^2}{k^2}

k_i(t) = m \Bigl ( \frac{t}{t_i} \Bigr )^{1/2}

Find probability \( P(k' \leq К) \) of a randomly selected node to have \( k \leq k \) at time \( t \) (fraction of nodes with \( k’ < k \) ). Nodes with \( k_i(t) \leq l \) :

t_i \geq \frac{m^2}{k^2} t

\longrightarrow

Preferential attachment model

m = 1

m = 2

m = 3

Preferential attachment model

1. Growth

Node degree distribution function:

k_i(t) = m (1 + log(\frac{t}{i}))

P(k) = \frac{e}{m}exp(-\frac{k}{m})

П(k_i) =\frac{1}{n_0 + t + 1}

Node degree growth:

At each time step add a new node with \( m \) edges \( (m \leq n_0) \) ,
connecting to т nodes already in network \(k_i(i) = m \)

2. Attachment uniformly at random

The probability of linking to existing node \( i \) is

Preferential attachment model

Power law distribution function:

Clustering coefficient (numerical result):

< L > \sim \frac{log(N)}{log(log(N))}

P(k) = \frac {2m^2}{k^3}

Average path length (analytical result) :

C \sim N^{-0.75}

Preferential attachment model

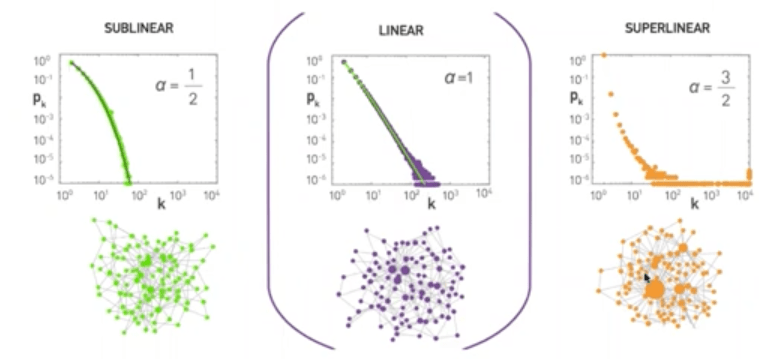
Non-linear preferential attachment models:

П(k) \sim k^{\alpha}

\( \alpha = 0 \) , no hubs, exponential dsitribution
\( 0 < \alpha < 1 \), sublinear, smaller hubs, stretched exponential
\( \alpha = 1 \) , scale-free, hubs, power law
\( \alpha > 1 \), superlinear, super hubs, hubs-and-spoke

Historical note

Polya urn model, George Polya, 1923
Yule process, Udny Yule, 1925
Distribution of wealth, Herbert Simon, 1955
Evolution of citation networks, cumulative advantage, Derek de Solla Price, 1976
Preferential attachment network model, Barabasi and Albert, 1999

Local random models vs global optimization models

Network models

Empirical Network Features

Power-law (heavy-tailed) degree destribution
Small average distance (graph diameter)
Large clustering coefficient (transitivity)
Giant connected component, hierachical structure,etc

Generative models

Random graph model (Erdos & Renyi, 1959)
Preferential attachement model (Barabasi & Albert, 1999)
Small world model (Watts & Strogatz, 1998)

Empirical Network Features

Power-law (heavy-tailed) degree destribution
Small average distance (graph diameter)
Large clustering coefficient (transitivity)
Giant connected component, hierachical structure,etc

Generative models

Random graph model (Erdos & Renyi, 1959)
Preferential attachement model (Barabasi & Albert, 1999)
Small world model (Watts & Strogatz, 1998)

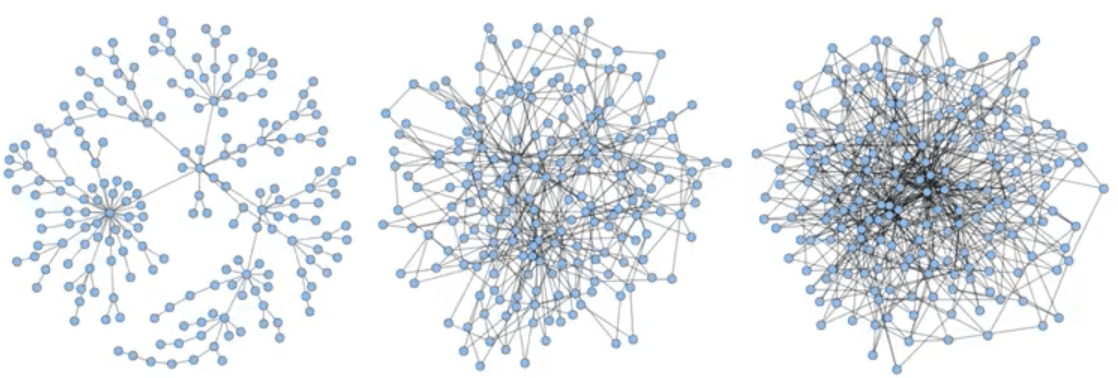
G(n, p) Model

In the \( G(n, p) \) model, a graph is constructed by connecting nodes randomly. Each edge is included in the graph with probability \( p \) independent from every other edge. Equivalently, all graphs with \( n \) nodes and \( m \) edges have equal probability of \( p^m(1-p)^{(\frac{n}{2}-m)} \)

Erdos and Renyi, 1959.

\langle m \rangle = p \frac{n(n − 1)}{2}

\( G_{n,p} \) , each pair out of \( n(n − 1)/2 \) pairs of nodes is connected with probability \( p \), \( m \) - random number, \( \langle k \rangle \) - average node degree

\langle k \rangle = \frac{1}{n} \sum_i{k_i}=\frac{2 m }{n}=p(n-1) \approx pn

G(n, p) Model

Probability that \( i \) -th node has a degree \( k_i = k \)

(Bernoulli distribution)

\( p^k \) - probability that connects to k nodes (has k-edges)
\( (1 − p)^{n−k−1} \) - probability that does not connect to any other node
\( C^k_{n-1} \) - number of ways to select k nodes out of all to connect to

P(k_i = k) = P(k) = C^k_{n-1}p^k(1-p)^{n-1-k}

Limiting case of Bernoulli distribution, when \( n → ∞ \) at fixed \( \langle k \rangle = pn = λ \) (see upper formula)

P(k) = \frac{\langle k \rangle^ke^{-\langle k \rangle}}{k!}=\frac{λ^ke^{-λ}}{k!}

G(n, p) Model

Poisson distribution

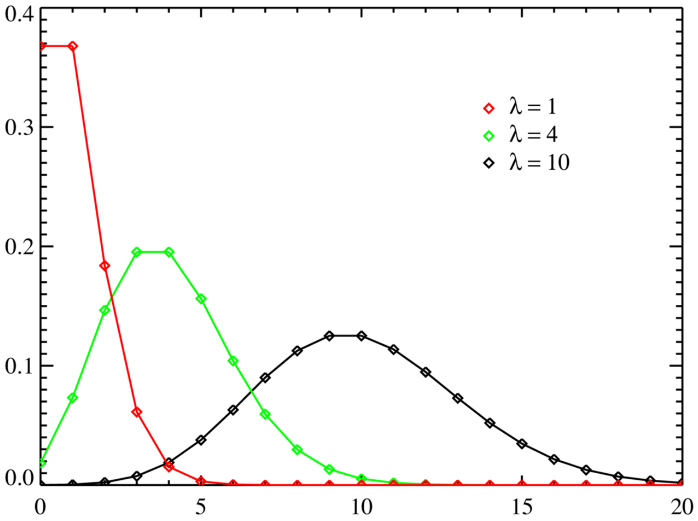
Phase Transition

Consider \( G_{n,p} \) as a function of \( p \)

\( p = 0 \), empty graph
\( p = 1 \), complete (full) graph
There are exist critical \( p_c \) , structural changes from \( p < p_c \) to \( p > p_c \)
Gigantic connected component appears at \( p > p_c \)

Let \( u \) - fraction of nodes that do not belong to GCC. The probability that a node does not belong to GCC

u = p(k=1)•u + P(k=2)•u^2 + P(k=3)•u^3 ... =

= \sum_{k=0}^∞{P(k)u^k} = \sum_{k=0}^∞ \frac{λ^ke^-λ}{k!}= e^{-λ}e^{λu} = e^{λ(u-1)}

Phase Transition

Let \( s \) -fraction of nodes belonging to GCC (size of GCC)

when \( λ \rightarrow ∞, s \rightarrow 1 \)
when \( λ \rightarrow 0, s \rightarrow 0 \)
\( λ=pn \)

s = 1 — u

1-s=e^{-λs}

\( λ_c = p_cn = 1 \)
\( p_c = \frac{1}{n} \)

Small world model

Threshold probabilities when different subgraphs of g-nodes appear in a random graph

\( p_c \sim n^{-g/(g-1)} \) having a tree of order \( g \)
\( p_c \sim n^{-1} \), having a cycle of order \( g \)
\( p_c \sim n^{-2/(g-1)} \) complete subgraph of order \( g \)

s = 1 — u

1-s=e^{-λs}

\( λ_c = p_cn = 1 \)
\( p_c = \frac{1}{n} \)

03-2

Small world

Small world model

Motivation: keep high clustering, get small diameter

Clustering coefficient С = 1/2
Graph diameterd = 8

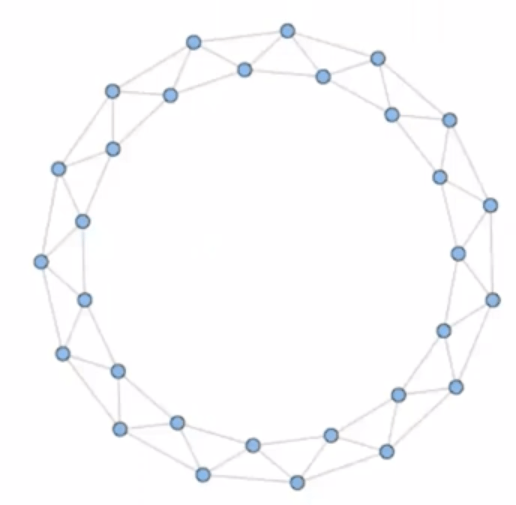
Small world model

Single parameter model, interpolation between regular lattice and random graph

start with regular lattice with п nodes, К edges per vertex (node degree), \( k << n \)
randomly connect with other nodes with probability р, forms \( pnk/2 \) "long distance” connections from total of \( nk/2 \) edges
\( р = 0 \) regular lattice, \( р = 1 \) random graph

Watts and Strogatz, 1998

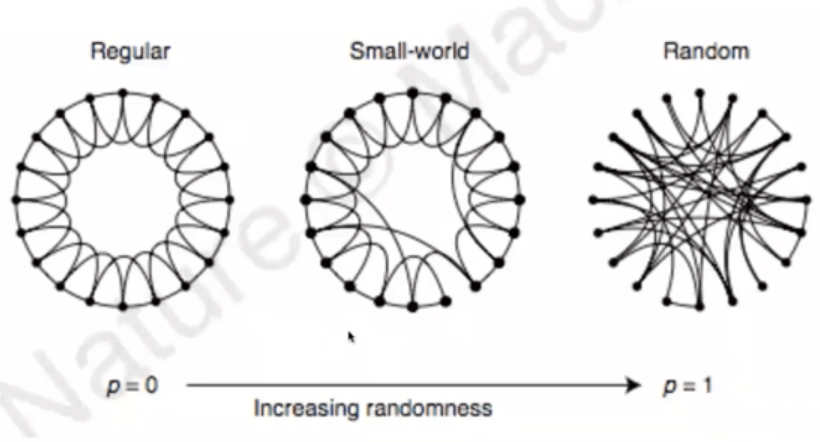
Small world model

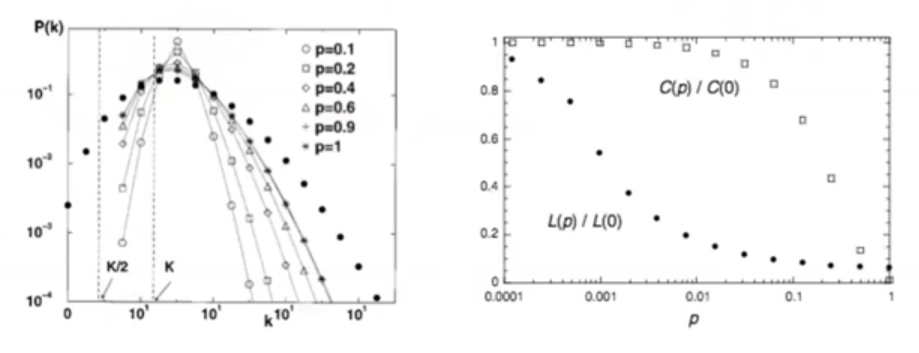
Node degree distribution:
Poisson like

Ave. path length \( \langle L(p) \rangle \) :
\( р \longrightarrow 0 \) , ring lattice, \( \langle L(p) \rangle = n/2k \)
\( р \longrightarrow 1 \) , random graph, \( \langle L(p) \rangle = log(n)/log(k) \)

Clustering coefficient C(p) :
\( р \longrightarrow 0 \) , ring lattice, C(0) = 3/4 = const
\( р \longrightarrow 1 \) , random graph, С(1) = k/n

Small world model

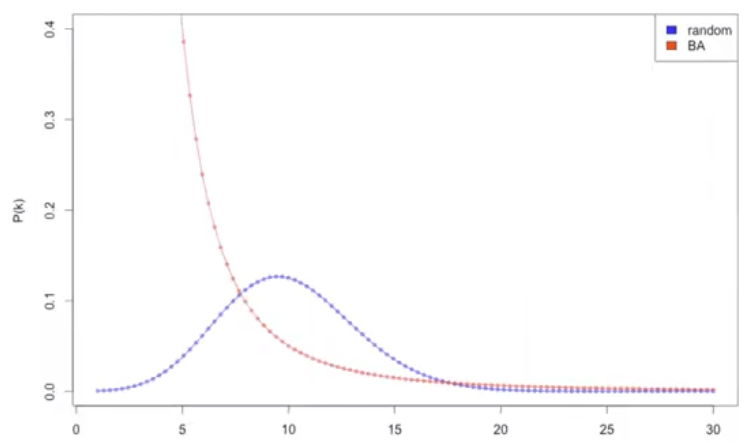
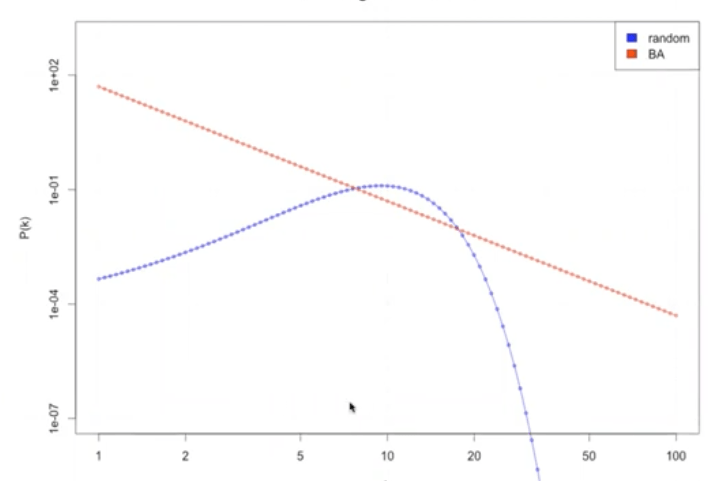
Model comparison

	Random	BA	WS	Empiracal nets
			poisson like	power law
			const	large
				small

\frac{\lambda^k e^{-\lambda}}{k!}

\langle k \rangle / N

\frac{log(N)}{log(\langle k \rangle)}

\frac{log(N)}{log(log(\langle k \rangle))}

log(N)

k^{-3}

N^{-0.75}

P(k)

\langle L \rangle