Knapsack Problem
(背包問題)

How to be a smart thief?

Carrying capacity is limited

Of course, the thief will try his best to take out the maximum value in his backpack

A thief, An apartment (no one is there)

radio	laptop	guitar
$30,000	$20,000	$15,000
4kg	3kg	1kg

Capacity: 4 kg

Grokking Algorithms: An illustrated guide for programmers and other curious people. Ch9 p161

A simple way...

Put 📻 into 📦

or
Don't put 📻 into 📦

Put 💻 into 📦

or
Don't put 💻 into 📦

Put 🎸 into 📦

or
Don't put 🎸 into 📦

Grokking Algorithms: An illustrated guide for programmers and other curious people. Ch9 p161

A simple way...

Put 📻 into 📦

or
Don't put 📻 into 📦

Put 💻 into 📦

or
Don't put 💻 into 📦

Put 🎸 into 📦

or
Don't put 🎸 into 📦

2 x 2 x 2 = 8

Your bag	empty = $0	📻 = $30,000
💻 = $20,000	🎸 = $15,000	📻 💻 = $50,000
💻 🎸 = $35,000	📻 🎸 = $45,000	💻 📻 🎸 = $65,000

If there were one more extra item ...

the thief need to calculate of possiblities

2^n

If there were 10 items, the thief would calculate of possibilities, which is equal to 1,024

2^{10}

If there were one more extra item ...

stackoverflow : if n^3 has a fast rate of ...

Besides maximum value, the thief hasn't considered the weight yet, coz the bag has a capacity limit.

Your bag	empty = $0	📻 = $30,000
💻 = $20,000	🎸 = $15,000	📻 💻 = $50,000
💻 🎸 = $35,000	📻 🎸 = $45,000	💻 📻 🎸 = $65,000

Besides maximum value, the thief hasn't considered the weight yet, coz the bag has a capacity limit.

x

Your bag capacity : 4 kg	empty = $0 (v) waste to check	📻 = $30,000 4kg (v)
💻 = $20,000 3kg (v)	🎸 = $15,000 1kg (v)	📻 💻 = $50,000 ~~7kg~~ (x)
💻 🎸 = $35,000 4kg (v)	📻 🎸 = $45,000 ~~5kg~~ (x)	💻 📻 🎸 = $65,000 ~~8kg~~(x)

How to be smart?

Let's take out your notebook

Step 1

1. Divide the backpack into a smaller backpack.

If we can solve the max value of 1 kg and 3 kg bag, then we can solve the max value of 4 kg bag.

Capacity: 4 kg

Capacity: 1 kg

Capacity: 3 kg

Step 2

2. Take a note of the max value on every small bags

Then we can store it for future usage, that is to say, we can make a comparison of the max value on each item.

📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg

Your notebook

1. Divide the backpack into a smaller backpack.

2. Calculate the maximum value of each backpack.

3. Record the maximum value on the table

	📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg
🎸 1kg

Your notebook

$15000
🎸

📻	💻	🎸
$30,000	$20,000	$15,000
4kg	3kg	1kg

	📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg
🎸 1kg	$15000 🎸	$15000 🎸	$15000 🎸	$15000 🎸
📻 4kg

Your notebook

📻	💻	🎸
$30,000	$20,000	$15,000
4kg	3kg	1kg

$15000
🎸

$30000
📻

📻 or 👆

	📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg
🎸 1kg	$15000 🎸	$15000 🎸	$15000 🎸	$15000 🎸
📻 4kg	$15000 🎸	$15000 🎸	$15000 🎸	$30000 📻
💻 3kg

Your notebook

📻	💻	🎸
$30,000	$20,000	$15,000
4kg	3kg	1kg

$15000
🎸

💻 or 👆

$20000
💻

💻 + 1 or 👆

$35000
💻 🎸

What if the thief saw an iPhone before he left?

📱 $20,000 /
1kg

Grokking Algorithms: An illustrated guide for programmers and other curious people. Ch9 p171

	📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg
🎸 1kg	$15000 🎸	$15000 🎸	$15000 🎸	$15000 🎸
📻 4kg	$15000 🎸	$15000 🎸	$15000 🎸	$30000 📻
💻 3kg	$15000 🎸	$15000 🎸	$20000 💻	$35000 💻 🎸
📱 1kg

Your notebook

📻	💻	🎸	📱
$30,000	$20,000	$15,000	$20,000
4kg	3kg	1kg	1kg

📱 or 👆

$20000

📱

📱+ 1 or 👆

📱+ 2 or 👆

📱+ 3 or 👆

$35000

📱🎸

$35000

📱🎸

$40000

📱 💻

We made it!

	📦capacity: 1 kg	📦capacity: 2 kg	📦capacity: 3 kg	📦capacity: 4 kg
🎸 1kg	$15000 🎸	$15000 🎸	$15000 🎸	$15000 🎸
📻 4kg	$15000 🎸	$15000 🎸	$15000 🎸	$30000 📻
💻 3kg	$15000 🎸	$15000 🎸	$20000 💻	$35000 💻 🎸
📱 1kg	$20000 📱	$35000 📱🎸	$35000 📱🎸	$40000 📱💻

We made it!

	small bag1 capacity	small bag2 capacity	...	bag W capacity
item 1 weight
item 2 weight
...
item n weight

We made it!

Our calculation time was , but what about now?

is the amount of items

2^n

n

The calculation time is now.

n*W

is the amount of all kinds of backpack

W

Complexity?

	Time	Space
Exhaustive method
Dynamic programming

O(2^n)

O(1)

O(nW)

0-1 Knapsack Problem | DP-10

Complexity?

stackoverflow : if n^3 has a fast rate of ...

Divide a problem into sub-problems.
Solve each sub-problems and store it for future usage

Dynamic Programming

Lovely Rabbits

5

0

1

4

2

3

month	pair
0	1
1	1
2	2
3	3
4	5
5	8

Find out the regular pattern

The number of rabbits will be the same as the previous month at least.
It takes 2 months to give birth since the rabbits are born.

The life of rabbits is eternal.
Every rabbit can only give birth to male and female twins every time.

Assume

Clue

Fibonacci Problem

f(0)=1

f(1)=1

f(n)=f(n-1)+f(n-2)

for n > 1,

function fibonacci(num) {
  if (num <= 1) return 1;
  return fibonacci(num - 1) + fibonacci(num - 2);
}

The number of rabbits will be the same as the previous month at least.
It takes 2 months to give birth since the rabbits are born.

Clue

f(n-1)

f(n-2)

Fibonacci Problem

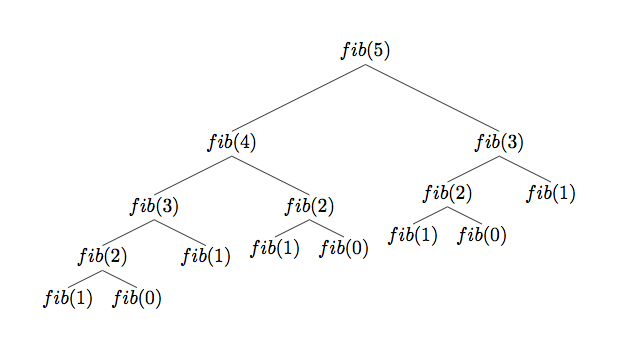
Introduction to Dynamic Programming

Our calculation time is almost about .

2^n

How to be smart?

Let's take out your notebook

How to be smart?

1. Can we divide the program into sub-programs?

2. Can we store something first and use it later?

month	pair
0
1
2
3
4
5

Wrote down the result in your notebook

f(5)

f(4)

f(3)

f(2)

f(1)

f(0)

1

2

3

5

8

month	pair
0	1
1	1
2	2
3	3
4	5
5	8

Wrote down the result in your notebook

f(5)

f(4)

f(3)

f(2)

f(1)

f(0)

month	pair
0	1
1	1
2	2
3	3
4	5
5	8
6
7

Can I know ?

f(7)

f(6)

f(5)

f(4)

f(7)

13

21

f(5)

Complexity?

	Time	Space
Exhaustive method
Dynamic programming

O(2^n)

O(1)

O(n)

0-1 Knapsack Problem | DP-10

almost

Complexity?

stackoverflow : if n^3 has a fast rate of ...

Exercise

What if there were a watch?

⌚
$17,000 /
0.5 kg

Grokking Algorithms: An illustrated guide for programmers and other curious people. Ch9 p171

	📦: 1	📦: 2	📦: 3	📦: 4
🎸
📻
💻
📱

	📦: 0.5	📦: 1	📦: 1.5	📦: 2	📦: 2.5	📦: 3	📦: 3.5	📦: 4
🎸
📻
💻
📱
⌚

Can he steal some of rice if there were a bag of rice?

Grokking Algorithms: An illustrated guide for programmers and other curious people. Ch9 p171

$40,000 /
5 kg

4 kg

Fibonacci Problem

function fibonacci(num) {
  if (num <= 1) return 1;
  return fibonacci(num - 1) + fibonacci(num - 2);
}

Implement in Dynamic Programming way

Reference

Grokking Algorithms: An illustrated guide for programmers and other curious people (Traditional Chinese Edition)
Demystifying Dynamic Programming
JavaScript Algorithms and Data Structures Masterclass
Dynamic Programming - Learn to Solve Algorithmic Problems & Coding Challenges
Fibonacci sequence algorithm in Javascript

Illustration & Material

vectorpocket: Three-story house interior...

Adobe Stock: Thief

Photoplotnikov: Big knotted sack

vexels: Electric guitar

jemastock : Old radio stereo vector image

588ku: Taking Notes Business Style

Creative Fabrica: Laptop Vector Illustration...

Ruslanchik: Empty sack

Dynamic Programming

Knapsack Problem(背包問題)

How to be a smart thief?

A thief, An apartment (no one is there)

A simple way...

A simple way...

2 x 2 x 2 = 8

If there were one more extra item ...

If there were one more extra item ...

How to be smart?

Let's take out your notebook

Step 1

Step 2

Your notebook

Your notebook

Your notebook

Your notebook

What if the thief saw an iPhone before he left?

Your notebook

We made it!

We made it!

We made it!

Complexity?

Complexity?

Dynamic Programming

Lovely Rabbits

Find out the regular pattern

Fibonacci Problem

for n > 1,

Fibonacci Problem

How to be smart?

Let's take out your notebook

How to be smart?

Complexity?

Complexity?

Exercise

What if there were a watch?

Can he steal some of rice if there were a bag of rice?

Fibonacci Problem

Recap

Reference

Illustration & Material

Knapsack Problem
(背包問題)