自我介紹

- 張程凱 (ZCKevin)
- 臺北市立建國高級中學
- 台大資工系 (大一)
- 2021 IOI Silver (rk 39)
- 高一沒進選訓,高二一階,高三三階
Brain Storm
AGC 047E
(此題為 output only)
有個序列 \(a_0, a_1,...a_{N-1}\)。
最一開始的時候 \(a_0 = A, a_1 = B, a_2...a_{N-1} = 0\)。
你希望經由一些操作之後 \(a_3 = A \times B\),以下是你可以進行的操作。
- + i j k:令 \(a_k := a_i + a_j\)
- < i j k:令 \(a_k := [a_i < a_j]\)
而你最多能進行 Q 次操作。
\(N = Q = 200000\)
\(0 \le A, B \le 10^9\)
CF 1086F
有個無限大二維平面
在第 0 秒有 \(N \le 50\) 個格子\((x_0, y_0),...(x_{N-1}, y_{N-1}))\)在燃燒。而在第 \(t \le 10^8\) 秒的時候,所有的格子都會立刻停止燃燒。
假設某個格子在燃燒,過了恰一秒後,它八方位的格子也都會開始燃燒。
定義 \(f(x, y)\) 代表座標 \((x,y)\)起火的時間。
我們想計算 \(\sum f(x, y) \pmod{998244353}\)
次小值的妙用
例題1:
有 \(A_1, A_2...A_N\), \(B_1, B_2...B_N\)
和 \(Q\) 筆操作
- \(\text{A x, y} : A_x := y\)
- \(\text{B x, y} : B_x := y\)
- \(\text{Q l, r, c} :\) 求 \[\max_{l \leq i \leq r, B_i \neq c}(A_i)\]
\(N, Q \leq 10^6\)
\(A_i, B_i \leq 10^{18}\)
其他例題們
cscademy MST and rectangle
tioj 1793
不同的東西
CSA Election Spies
有 \(N\) 個球,其中恰有一個黑球,一個紅球,\(N-2\) 個怪球
你每次可以選一些球,然後看他們的顏色
- 如果你有選到黑球,且沒選到紅球 那你會看到所有球都是黑色的
- 如果你有選到紅球,且沒選到黑球 那你會看到所有球都是紅色的
- 如果你同時選到黑球和紅球,那黑球是黑色的,紅球是紅色的,其他的可能會是黑色也可能是紅色
- 假設你黑球和紅球都沒選到,那你選出來的球都可能會是黑色也可能是紅色。
最多可以做 \(Q\) 次
你想找出黑球和紅球分別是哪顆
\(N \leq 30000, Q = 60\)
其他例題們 :
IZHO 2019 Xoractive
tioj 1793
怪怪環問題
CSA xor cycle
給張帶權無向圖
求最大權的環
而一個環的權重定義為邊的權重 xor 合
\(|V| \leq 10^5, |E| \leq 2 \cdot 10^5\)
其他例題們 :
CF global round 14 pG
觀察力訓練
USACO 2017 R1 Triangles
平面上給定 \(N\) 個點
保證三點不共線
對於 \(1 \leq i \leq N-3\)
請輸出有多少個三角形內部恰有 \(i\) 個點
\(N \leq 300\)
CSA Tree Square
定義一張圖 \(G\) 的平方 \(G^2\) :
如果 \(i, j\) 有連邊若且唯若在 \(G\) 上面
\(distance(i, j) \leq 2\)
給你 \(G^2\),且 \(G\) 保證是一棵樹
請還原一組合法的 \(G\)
\(|V| \leq 333\)
CSA surround the enemy
給 \(N \times M\) 的 grid
在 \(sx, sy\) 上面有寶藏,你想保護它不讓外面的人能走到寶藏的地方
在 \(i, j\) 上面蓋城堡的 cost 為 \(A_{i,j}\)
格子是8連通
就最小cost
\(N, M \leq 150, A_{i,j} \leq 10^9\)
BOI 2009 Triangulation
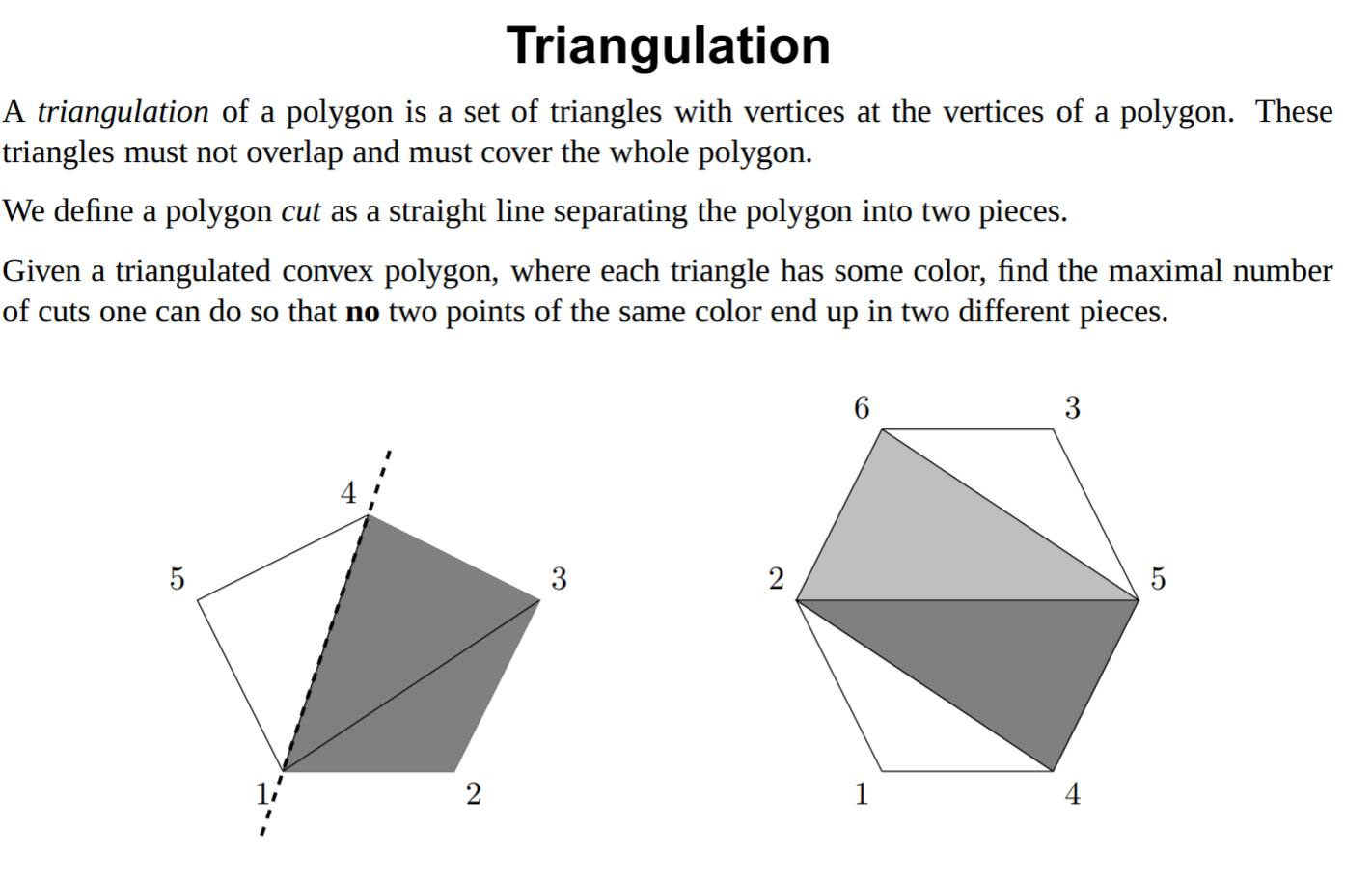
\(N \leq 10^5\)
CSA Binary Swaps
給個 01 序列 \(A_1, A_2...A_N\)
每隔一秒 對於所有 \(i\) 只要 \(A_i = 0, A_{i+1} = 1\)
那 \(A_i, A_{i+1}\) 就會被交換
請問 \(T\) 秒後 序列長怎樣
\(N, T \leq 10^6\)
JOISC 2016 Sandwich
桌上有 個三明治被擺放成 \(R\) 行 \(C\) 列。每個三明治都被沿主對角線或者次對角線分割成兩個小三明治。
一個小三明治僅當以下兩種情況都滿足時才不能被吃掉:
- 與該小三明治在同一個三明治中的另一個三明治還沒被吃掉;
- 與該小三明治兩條直角邊相鄰的另外兩個小三明治中有一個沒有被吃掉。
現在 JOI 君想問你,他吃掉每一個三明治時最少要吃掉多少個小三明治?
\(R, C \leq 400\) 時限 5 s
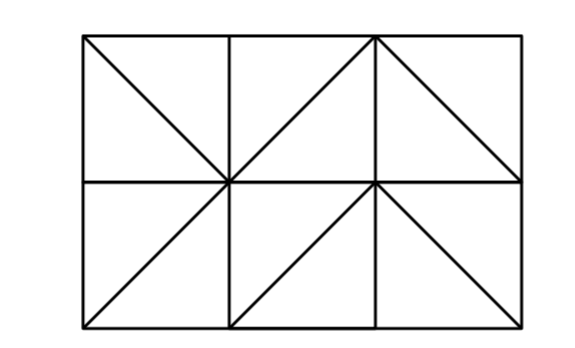
CSA anagram sort
有個隱藏序列,你想還原它
現在給你原始序列的 multiset
每次你可以 query 一種順序,
會回答你至少要做幾次交換相鄰元素,才能讓它變回原序列
可詢問次數 = 序列長度 + 1
AGC 016 pD

joisc 2016 Toilet
在比賽會場有恰一個男廁,女廁有 \(2N\) 個人排成一排要上廁所每次只要有廁所是空的 那:
- queue front 是男生 : 男廁空的話就去上,不然就禮讓後面第一位女生去女廁,並繼續等
- queue front 是女生 : 女廁空的話就去上,不然就去男廁
已知所有人上廁所皆需要一分鐘,你想重新安排隊伍,使得在 \(N\) 分鐘內所有人都能上完廁所。定義一種新的排隊順序 \(P\) 的權重為
\[\max_{1 \leq i \leq 2N} (\sum_{i < j}[P_j < P_i]) \]
求最小的合法排隊順序權重
一個字串 \(S\) 代表一種隊形, B=男生, G=女生
輸入為 \(M\) 個 pair \(S_i, T_i\) 代表字串 \(S_i\) 要重複 \(T_i\)次
\(N \leq 10^{18}, M \leq 10^5, \sum(|S_i|) \leq 2 \cdot 10^5\)
random 題
JOI 20 constellation 3
給很多高樓,以及星星,要拍一張長方形的照片,請問最大價值是多少?
