區間資料結構

（前綴、差分、線段樹、BIT、Sparse Table）

前綴

給一個序列 $A$ 長度為 $N$

有 $Q$ 筆詢問，求 $\sum\limits_{i = l}^r{A_i}$

Naive 作法：

一個迴圈搞定 ?
複雜度 $O(QN)$

$N \leq 10^5, Q \leq 10^5$

定義 $B_i := \sum\limits_{j=1}^{i}A_j$

$\sum\limits_{i=l}^{r}A_i = B_r - B_{l-1}$

時間複雜度 :

預處理 : $O(N)$
查詢 : $O(1)$

Atcoder Regular Contest 93 C

差分

給定序列 $A$

定義序列 $B_i := A_i - A_{i-1}$

為 $A$ 的差分序列

數線上有 $N$ 個線段

第 $i$ 個線段為 $[L_i, R_i]$

並且有 $Q$ 組詢問 $X_i$

回答在座標 $X_i$ 上面是否有線段經過

$N, Q, L_i, R_i, X_i \leq 10^5$

想辦法算出 $C_i := 座標 i 上的線段個數$

對於所有線段只要

在 $C_{L_i}$ 加一,

在 $C_{R_i+1}$ 減一

最後做一次前綴

有 $n$ 個線段起點終點分別為 $L_i, R_i$

並且有 $m$ 組詢問

$ql_i, qr_i$

回答是否存在線段 $L_j, R_j$ 使得

$L_j \leq ql_i , qr_i \leq R_j$

$n, m, L_i, R_i, ql_i, qr_i \leq 10^5$

定義 $right_i := \forall L_j \leq i, max(R_j)$

可透過前綴 max 來取得

Codeforces 1358F

給正整數序列 $A, B$ 長度皆為 $N$

你可以做很多次操作

幫 $A$ 做一次前綴和
把 $A$ reverse

你想要把 $A$ 變成 $B$
如果有解，請輸出一組可行解

$N \leq 10^5$

$A_i, B_i \leq 10^{18}$

sparse table

TIOJ 1603

給一個陣列 $A$
有 $Q$ 筆詢問

求 $(\forall L_i \leq j \leq R_i, max(A_j))$ -

$(\forall L_i \leq j \leq R_i, min(A_j))$

定義 $dp_{i,j}:= \forall i \leq k < i + 2^j, max(a_k)$

我們可得到下列關係式

$dp_{i,j} = max(dp_{i, j-1}, dp_{i+2^{j-1}, j-1})$

$dp_{i, 0} = a_i$

詢問 $[L, R)$

$k = \lfloor log_2 (R-L)\rfloor$

$max(dp_{L, k}, dp_{R-2^k, k})$

線段樹

Title Text

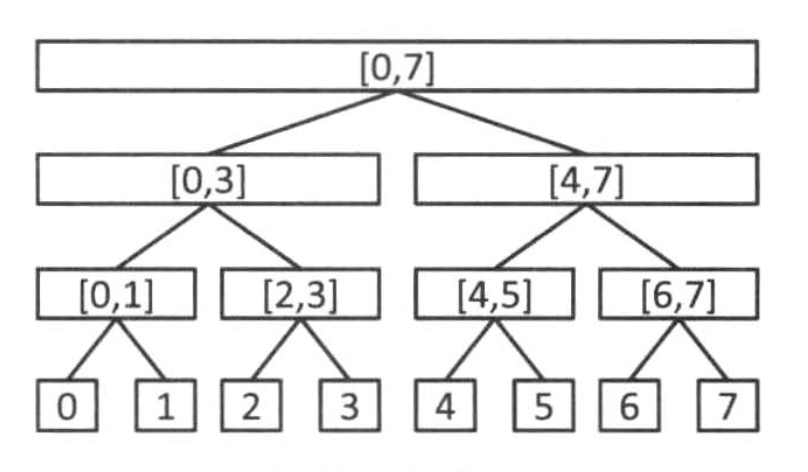
關於線段樹節點

假如一個節點代表了區間 $[L, R]$ 的資訊

而且有左右子樹 $[L, M], [M+1, R]$

當我想要算出 $max[L, R]$

我只要求 $max(leftchild, rightchild)$ 就好了

以指標來記錄左右子樹

struct segment_tree{
    struct node{
        int val;
        node* left = NULL, * right = NULL;
        node(int v):val(v){}
        void update() { val = max(left->val, right->val); }
        node(node* a, node* b){
            val = max(a->val, b->val);
            left = a, right = b;
        }
    };
    node* root;
    node* init(int l, int r, int* v){
        if(l == r)return new node(v[l]);
        int m = l + r >> 1;
        return new node(init(l, m, v), init(m+1, r, v));
    }
    void modify(int pos, int nv, node* now, int l = 1, int r = n){
        if(l == r) return now->val = nv, void();
        if(pos > r || pos < l)return;
        int m = l + r >> 1;
        modify(pos, nv, now->left, l, m);
        modify(pos, nv, now->right, m+1, r);
        now->update();
    }
    int query(int ql, int qr, node* now, int l = 1, int r = n){
        if(ql > r || qr < l) return -(1 << 29);
        if(ql <= l && r <= qr) return now->val;
        int m = l + r >> 1;
        return max(query(ql, qr, now->left, l, m),
                query(ql, qr, now->right, m+1, r));
    }
};

陣列形線段樹

以 1 作為根

對於節點 $i$ 以 $i*2, i*2+1$ 分別作為左右子樹

const int maxn = 1 << 20;
const int inf = 1 << 29;
struct segment_tree{
    int max_val[maxn << 1];
    void modify(int pos, int new_val, int l = 1, int r = n, int i = 1){
        if (l > pos || r < pos) return;
        if (l == r) return max_val[i] = new_val, void();
        int m = l + r >> 1;
        modify(pos, new_val, l, m, i<<1);
        modify(pos, new_val, m+1, r, i<<1|1);
        max_val[i] = max(max_val[i<<1], max_val[i<<1|1]);
    }
    int query_max(int ql, int qr, int l = 1, int r = n, int i = 1) {
        if (ql > r || qr < l) return -inf;
        if (ql <= l && qr >= r) return max_val[i];
        int m = l + r >> 1;
        return max(query_max(ql, qr, l, m, i<<1),
        		query_max(ql, qr, m+1, r, i<<1|1);
    }
};

Binary Indexed Tree

(Fenwick Tree)

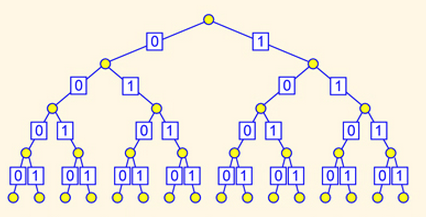
定義 $V_i := \sum\limits_{i - lowbit(i)+1}^{i} a_i$

$lowbit(i) := 2^{least significant bit(i)}$

x : 011010100

lowbit(x) : 000000100

Code

struct bit {
    int v[maxn];
    void add(int i, int val) {
        for (;i <= n;i += i&-i)
            v[i] += val;
    }
    int query(int i) {
        int res = 0;
        for (;i;i ^= i&-i)
            res += v[i];
        return res;
    }
}tree;

codeforces 1191F