分塊

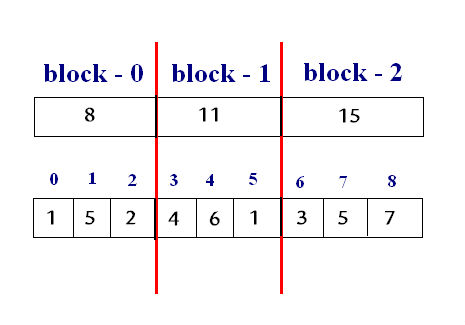
比較快的暴力

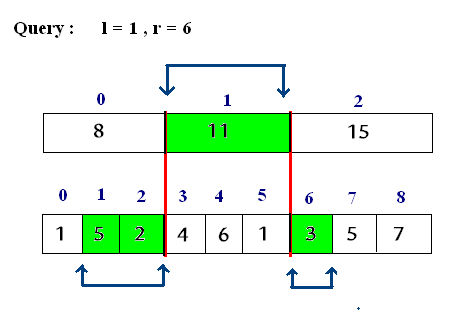
每 \(K\)個數字分為一塊，最多有\(n / K\)塊。

查詢時複雜度為\(\mathcal{O}(n / K + K)\)

修改時複雜度為\(\mathcal{O}(K)\)

整體複雜度\(\mathcal{O}(n / K + K)\)

如果我們想要讓\(n/k + k\)最小

根據算幾不等式 \(k + n/k \geq 2\sqrt {n/k\times k}\)

所以我們發現當\(k = n / k\)時

複雜度最好

中國人插隊問題

有\(n\)個人要排隊，但是因為有關係就沒關係，所以他們會插隊

\(1\ x\ id:\)編號為\(id\)的人直接插隊，排到第\(x\)個位置

\(2\ x:\)排在第\(x\)個位置的人走了

\(3\ x:\)詢問排在第\(x\)個位置的人的編號

有\(n\)筆操作

維護\(\sqrt n \)個 linked_list

每個 linked_list的大小為\(\sqrt n \)

插入時就到那一個 linked_list 暴力重建

並且把後面的 linked_list 都

把第一個元素塞到前一個 linked_list

刪除時亦然

查詢時複雜度為\(\mathcal{O}(\sqrt n)\)

修改時複雜度為\(\mathcal{O}(\sqrt n)\)

整體複雜度\(\mathcal{O}(n\sqrt n)\)

實做小技巧：

linked_list 寫起來很煩，所以既然std::deque 也有同樣的複雜度，那就用吧

題源：資訊之芽2019算法班講義

不那麼直覺的分塊

Codeforces 1207 F

給一個長度為\(n\)的序列，有\(m\)筆操作

\(1\ x\ y:\)把第 \(x\) 個數字加上 \(y\)

\(2\ x\ y: \)詢問 \( \sum_{i\in R(x, y)} a_i \)

定義\(R(x, y) = \{t : x \vert (t - y)\}\)

\(n, m \leq 500000\)

Counting Triangles

給一張圖，\(n\)個點 \(m\)條邊

詢問圖中有多少個三角形

對於三個點 \(a, b, c\) 如果 \(a, b\) 和 \(b, c\) 和 \(c, a\) 有邊，而且 \(a < b < c\) 那 \(a, b, c\) 就是一個三角形

\(n, m \leq 100000\)

假設我們能夠 \(\mathcal{O}(1) \)回答某個給定的 \(pair (x, y)\) 是否為圖上的一條邊
那麼指定任一個點 v，我們能夠

在 \(\mathcal{O}(m)\) 時間內算出圖中有幾個包含 v 的三角形
在 \(\mathcal{O}(d^2)\) 時間內算出圖中有幾個包含 v 的三角形（其中 \(d\) 為 v 的點度）

對於點度\(\leq K\)的點我們花\(\mathcal{O}(K^2)\)的時間做

剩下的點可以花\(\mathcal{O}(m \times c ^ 2)\)的時間做

定義\(c\)為點度\(\geq K\)的點的數量

如果令\(K := \sqrt m\)則

\(C \leq \sqrt m\)

所以每一個小點的時間需要\(\mathcal{O}(K^2)\)

所有大點需要\(\mathcal{O}(m \times c ^ 2)\)
小點最多有\(n\)個

最終複雜度為\(\mathcal{O}(m \sqrt m)\)