Networks and disease

Applications and inspiration from bighorn sheep

Pneumonia in bighorn sheep

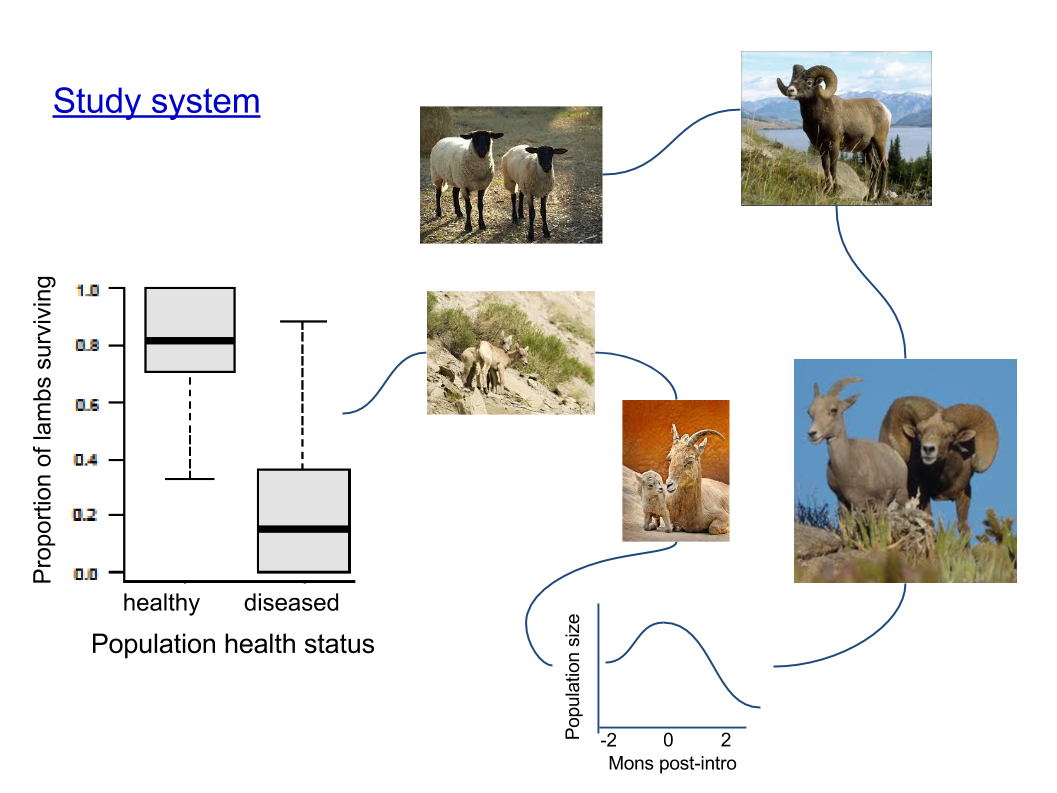
Cassirer et al. 2013, J Anim Ecol

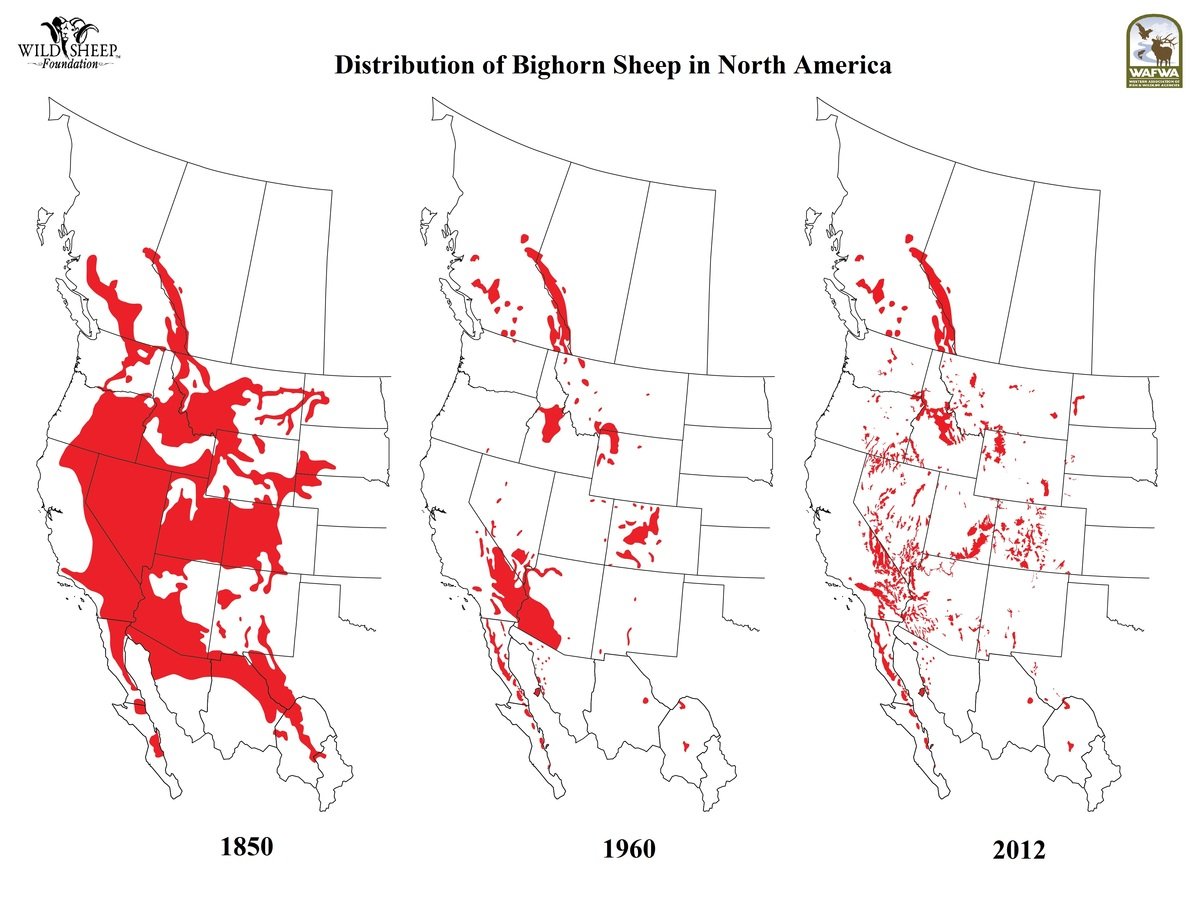
Source: Wild Sheep Foundation

Bighorn Health Consortium

Tom Besser,

Washington State

(vet microbiologist)

Frances Cassirer,

Idaho Dept Fish and Game

(wildlife biologist)

Raina Plowright

Montana State

Paul Cross, USGS

Pete Hudson,

Penn State

Conservation system

 

Challenges

  • Leverage all available information
  • Ask the right questions

 

Opportunities

  • Long-term data
  • Recently-established agent

Ph.D. program goals

 

1. Put forward the "most" urgent disease analyses based on existing data

 

2. Collect additional data on behavior and transmission (for states and funders)

 

3. Academic computing (for fellowship)

 

4. Basic science (for committee)

 

5. Technical support on collaborator projects

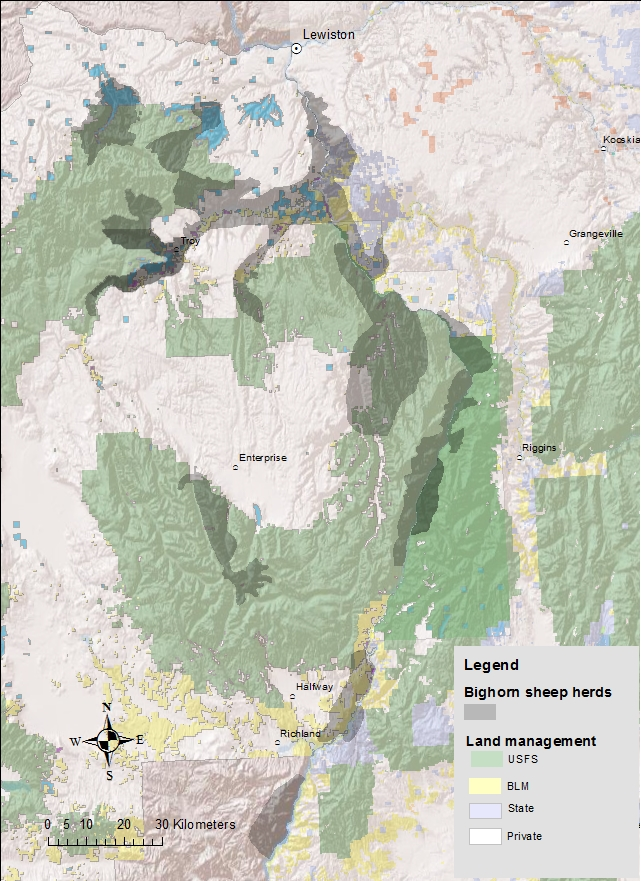
16 populations

Survey data since ~1970

Intensive study since 1996

500+ radiocollared animals

  • mix VHF/GPS
  • biweekly relocation interval (weekly in summer)

Lamb survival on ~700 lambs

Necropsies on

  • >200 adults,
  • >150 lambs

Longitudinal health sampling since 2011 in 3 populations

Pneumonia:

ephemeral or persistent?

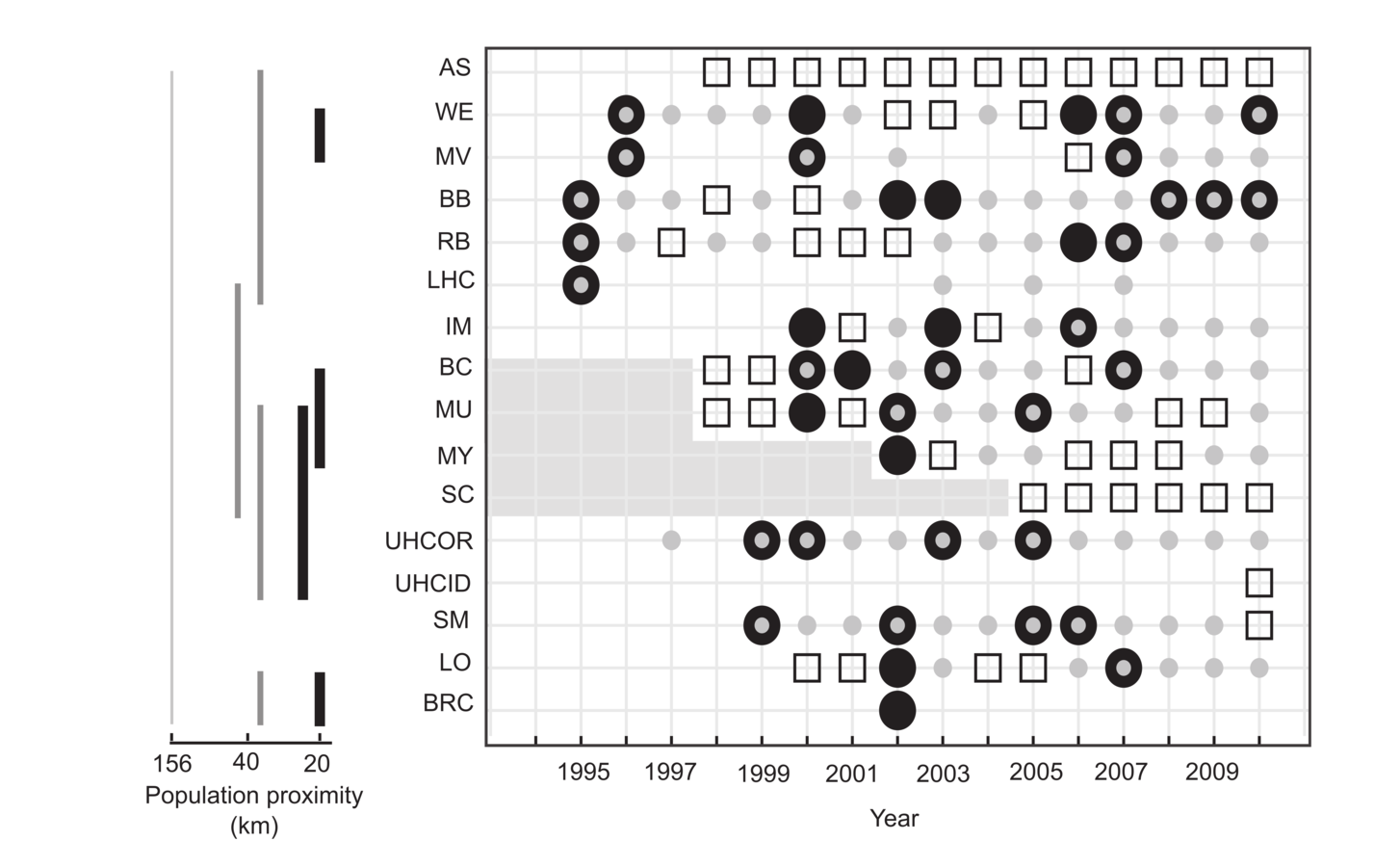
Healthy

Adult disease

Lamb disease

Populations

Cassirer et al. 2013, J Anim Ecol

Pathogen invasion stops population growth

Manlove et al. in review

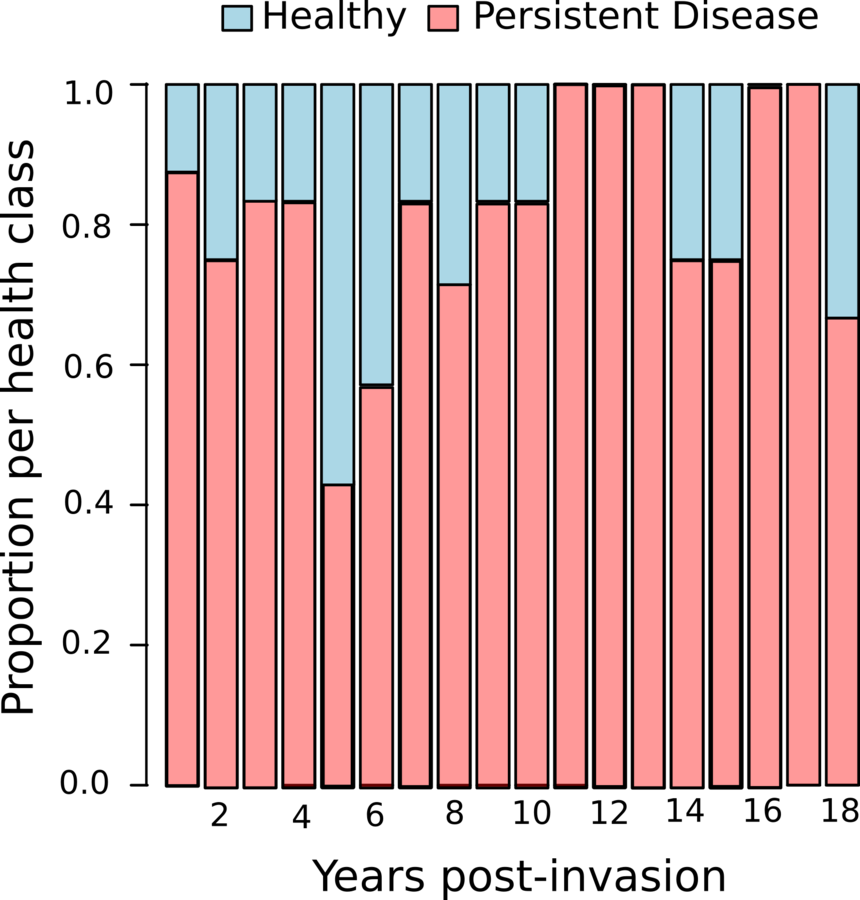
Manlove et al. in review

Years without documented pneumonia

Years with pneumonia

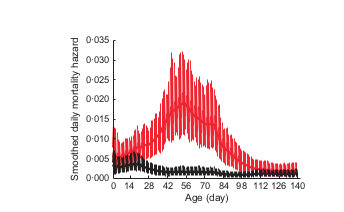
Age (days)

 

Smoothed daily mortality hazard

 

 

 

Cassirer et al. 2013, J Anim Ecol

Summer disease mortality asynchronous with typical ungulate juvenile mortality (over-winter)

Vital rates with and without disease

Objective:

combine multiple datastreams to draw inference to a single set of governing parameters

\mathbf{\sigma_{a}}, \mathbf{\phi_{a}}
σa,ϕa\mathbf{\sigma_{a}}, \mathbf{\phi_{a}}
\mathbf{Y_{1}} = f_{1}(\sigma_{a}, \phi_{a})
Y1=f1(σa,ϕa)\mathbf{Y_{1}} = f_{1}(\sigma_{a}, \phi_{a})
\mathbf{Y_{2}} = f_{2}(\sigma_{a}, \phi_{a})
Y2=f2(σa,ϕa)\mathbf{Y_{2}} = f_{2}(\sigma_{a}, \phi_{a})

(individual-level survival and reproduction)

(age-structured counts)

age-structured

survival

age-structured

P(wean a lamb)

Manlove et al. in review

Manlove et al. in review

What is the scale of transmission?

Are lamb mortalities well-mixed or localized to particular groups?

Well-mixed disease

Localized disease

=> low between-group variance

1) incomplete transmission, many sources

2) heterogeneous outcomes | infection

=> high between-group variance

1) localized infection

2) homogeneous outcomes | infection

Individuals

Sub-

populations

Years

Populations

Manlove et al. 2014 PRSB

Approach

1. Built networks using individual location data

2. ID'd groups (components)

3. Decomposed variance in lamb survival

log\left(\frac{p_{i}}{1 - p_{i}}\right) = subpop_{k[i]} + ewe_{j[i]}
log(pi1−pi)=subpopk[i]+ewej[i]log\left(\frac{p_{i}}{1 - p_{i}}\right) = subpop_{k[i]} + ewe_{j[i]}
subpop_{k} \sim N\left(year_{l[k]}, \tau_{subpop,PN} \times I(PN_{status})_{k} + \tau_{subpop,Healthy} \times (1 - I)PN_{Status})_{k}\right)
subpopk∼N(yearl[k],τsubpop,PN×I(PNstatus)k+τsubpop,Healthy×(1−I)PNStatus)k)subpop_{k} \sim N\left(year_{l[k]}, \tau_{subpop,PN} \times I(PN_{status})_{k} + \tau_{subpop,Healthy} \times (1 - I)PN_{Status})_{k}\right)
year_{l} \sim N\left(pop_{m[l]} + \delta I(PN_{Status})_{l}, \tau_{year,PN} \times I(PN_{status})_{l} + \tau_{year,Healthy} \times (1 - I)PN_{Status})_{l}\right)
yearl∼N(popm[l]+δI(PNStatus)l,τyear,PN×I(PNstatus)l+τyear,Healthy×(1−I)PNStatus)l)year_{l} \sim N\left(pop_{m[l]} + \delta I(PN_{Status})_{l}, \tau_{year,PN} \times I(PN_{status})_{l} + \tau_{year,Healthy} \times (1 - I)PN_{Status})_{l}\right)
pop_{m[l]} \sim N(0, \tau_{Pop})
popm[l]∼N(0,τPop)pop_{m[l]} \sim N(0, \tau_{Pop})
ewe_{j} \sim N(0, \tau_{ewe})
ewej∼N(0,τewe)ewe_{j} \sim N(0, \tau_{ewe})

i = individual lamb

j indexes ewes

k indexes groups in pops in years

l indexes pops in years

m indexes pops

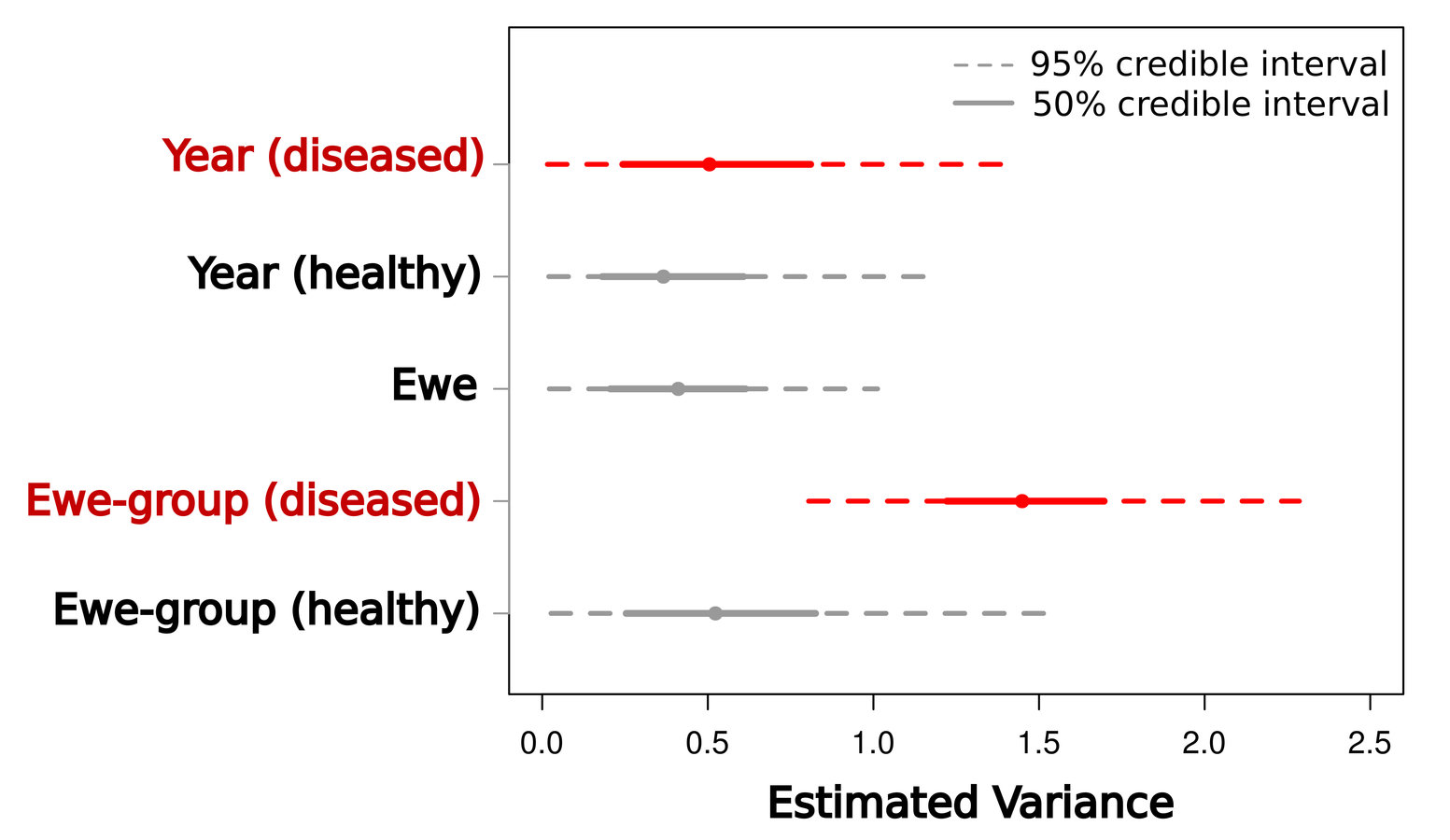
year_{l} \sim N\left(pop_{m[l]} + \delta I(PN_{Status})_{l}, \tau_{year,PN} \times I(PN_{status})_{l} + \tau_{year,Healthy} \times (1 - I)PN_{Status})_{l}\right)
yearl∼N(popm[l]+δI(PNStatus)l,τyear,PN×I(PNstatus)l+τyear,Healthy×(1−I)PNStatus)l)year_{l} \sim N\left(pop_{m[l]} + \delta I(PN_{Status})_{l}, \tau_{year,PN} \times I(PN_{status})_{l} + \tau_{year,Healthy} \times (1 - I)PN_{Status})_{l}\right)

Manlove et al. 2014 PRSB

Evidence that transmission is localized within groups.

Follow-up question:

How does population size relate to group size?

Manlove et al. 2014 PRSB

(components = groups)

# groups increases with pop size...

... while group size remains stable

Disease may behave like it's FD

+

Relatively constant number of potentially infectious contacts

...no (or very low) CCS.

Localized, fairly complete transmission with consistent, severe effects

Behavior and transmission risk

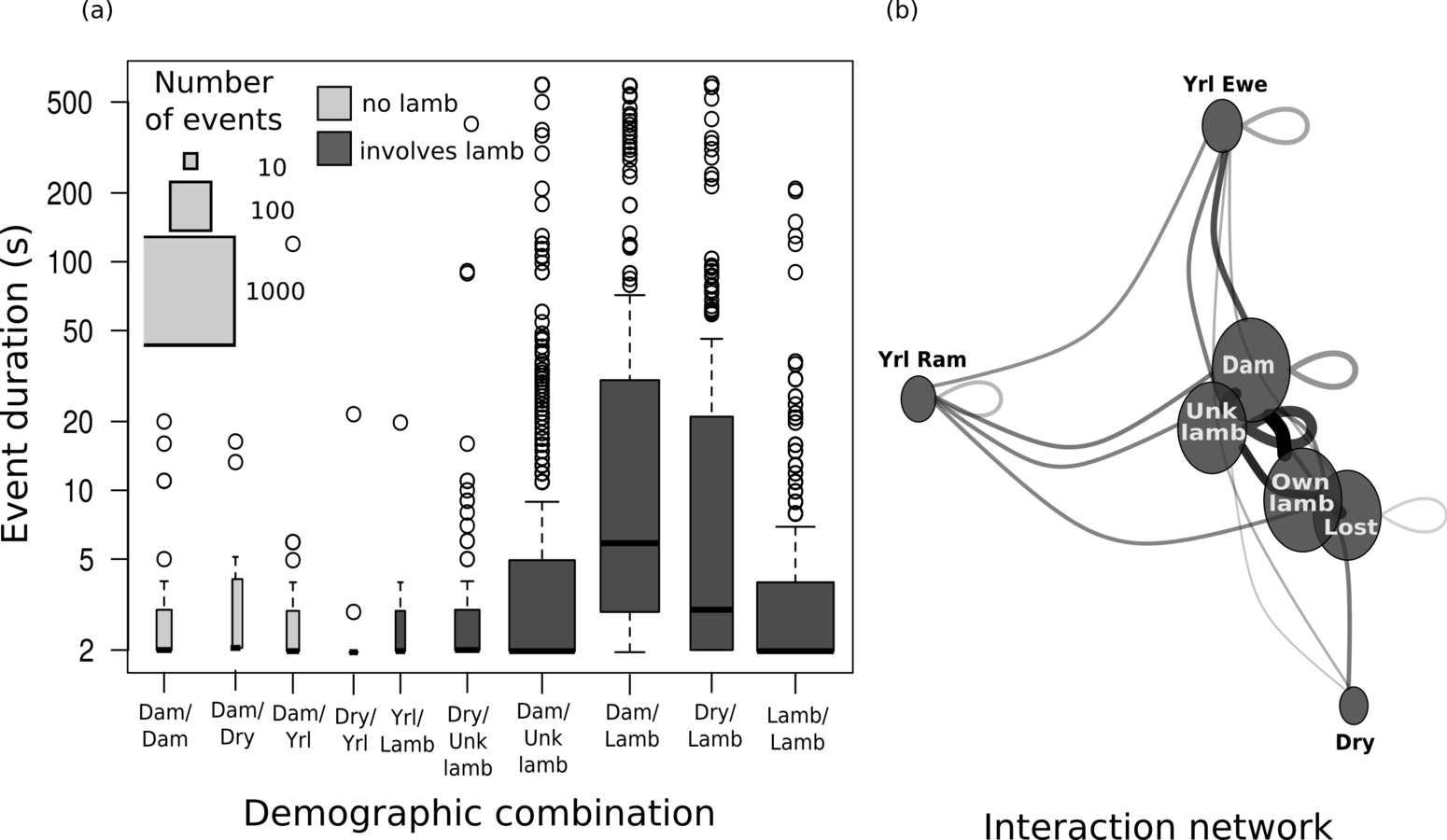
Association network

(Same place / same time)

(Direct touching)

Field data on bighorn behavior

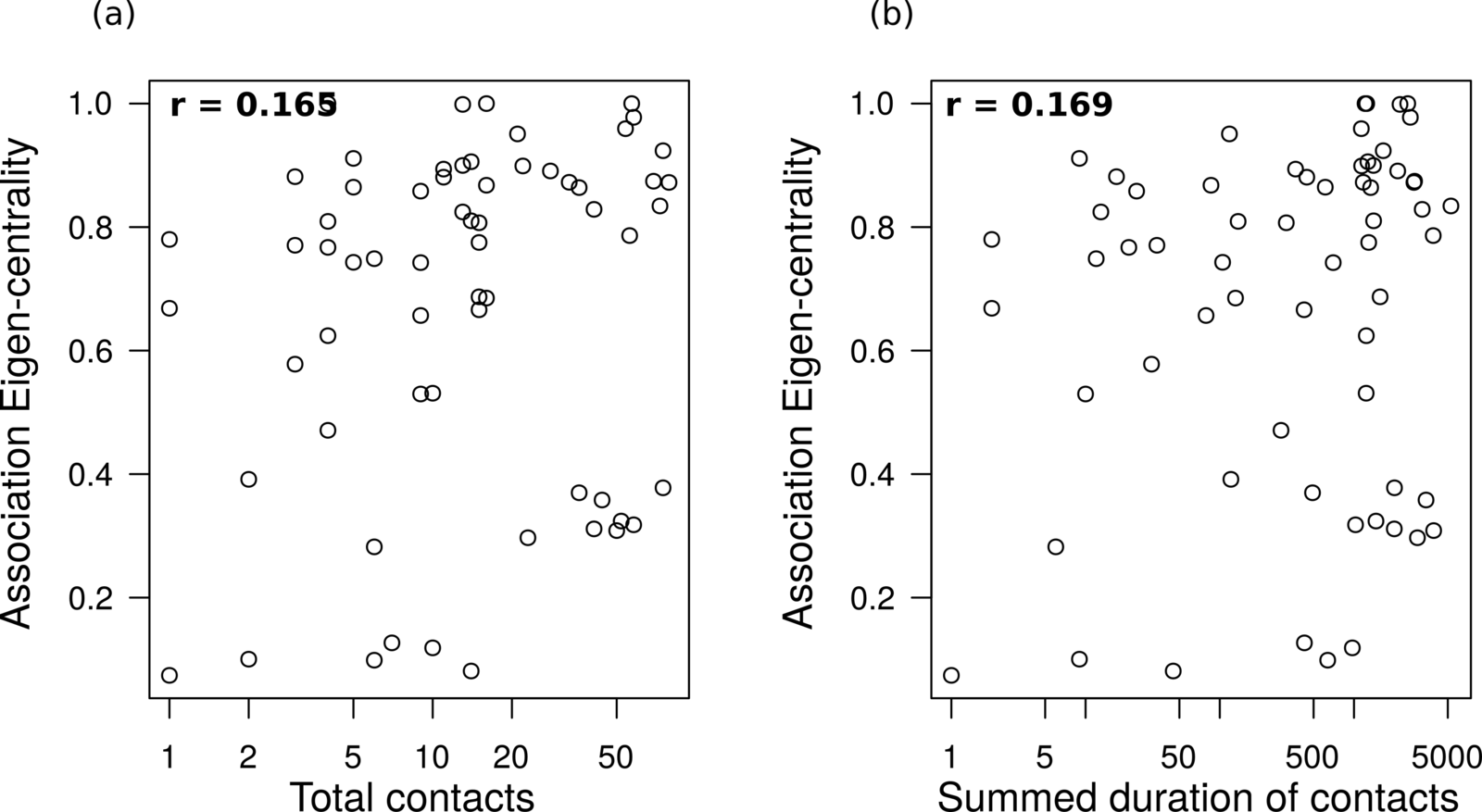
Association centrality and interaction intensities

are not  strongly correlated

 

Not all infecteds transmit.

Observation:

Can we use networks to infer something about P(transmission)?

Question:

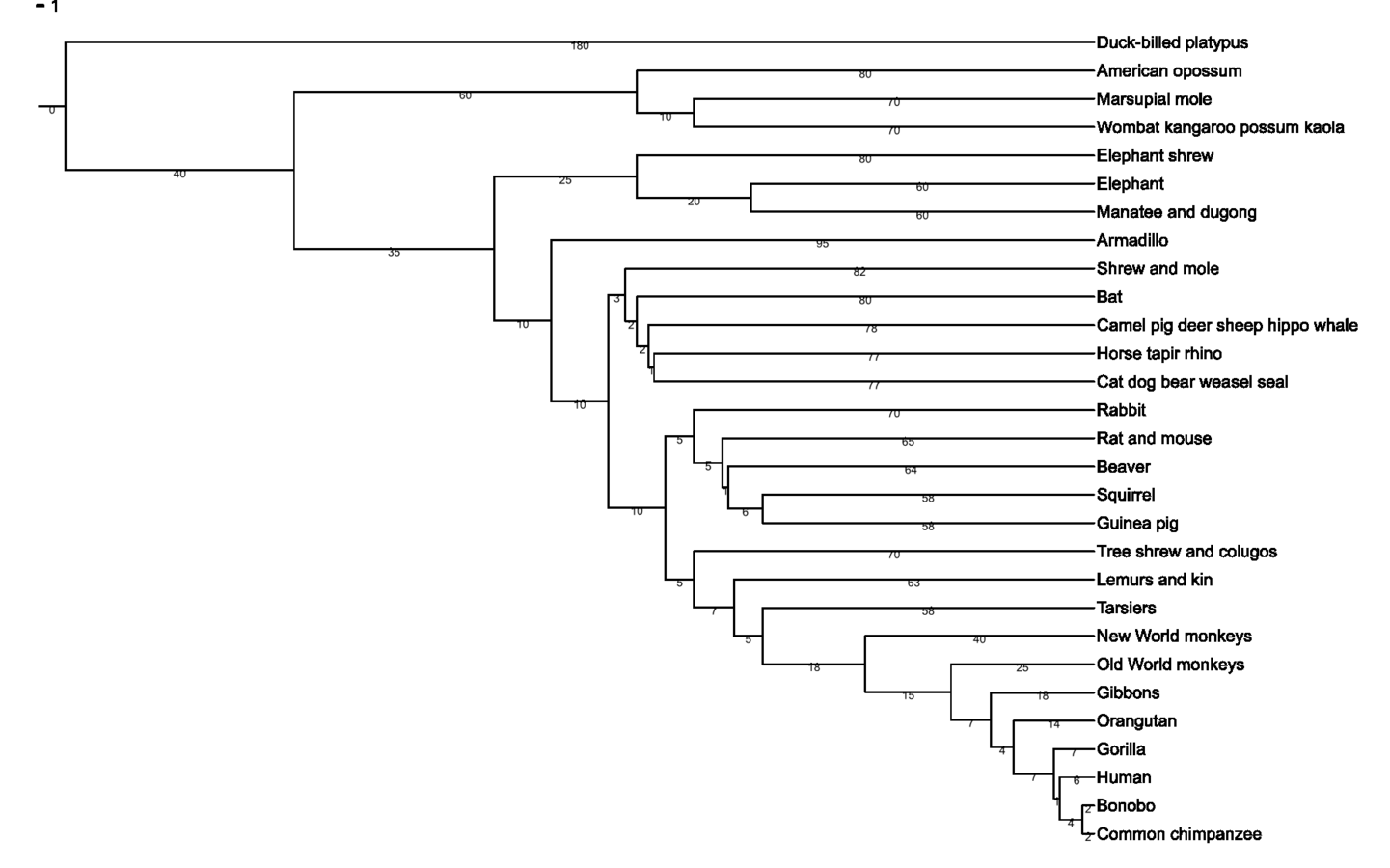
Ideas from adaptive evolution

*Butler and King (2004) Am Nat

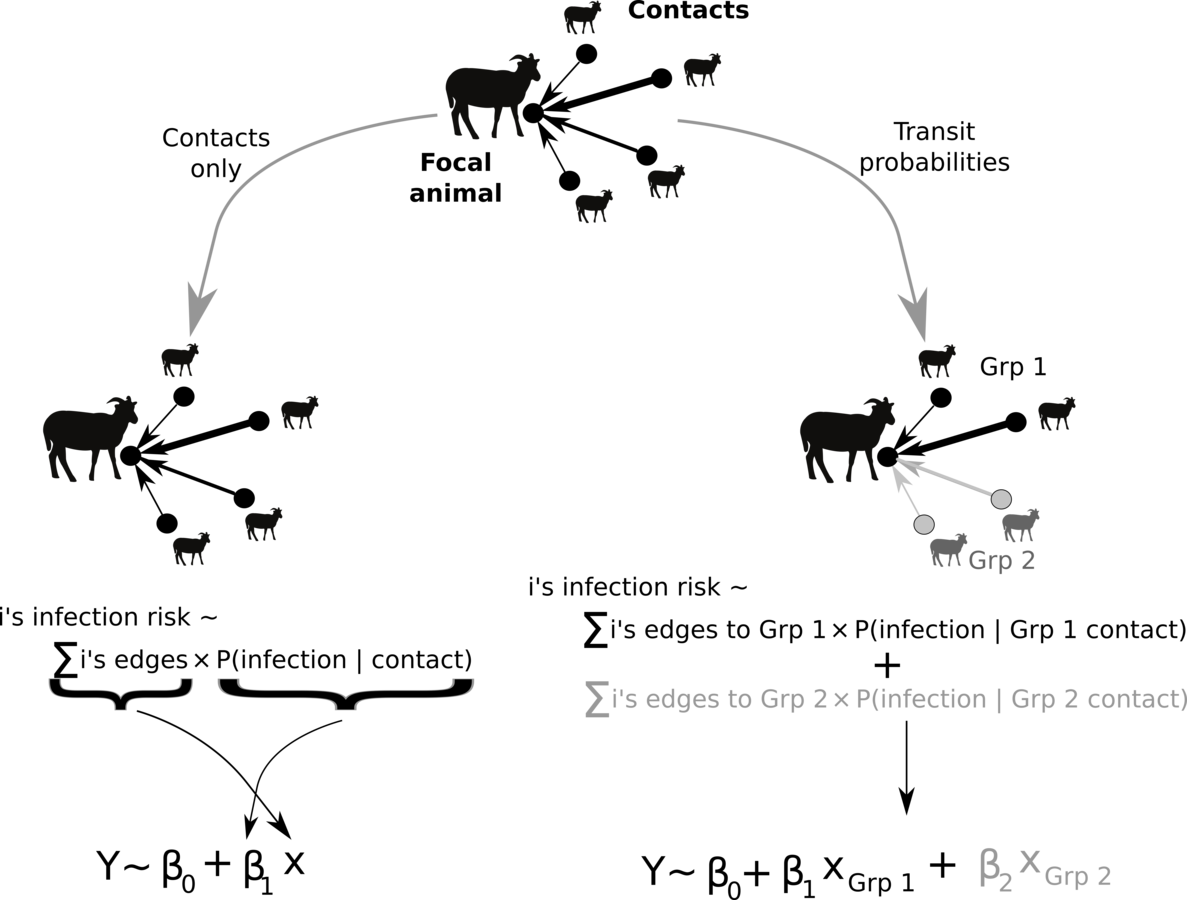
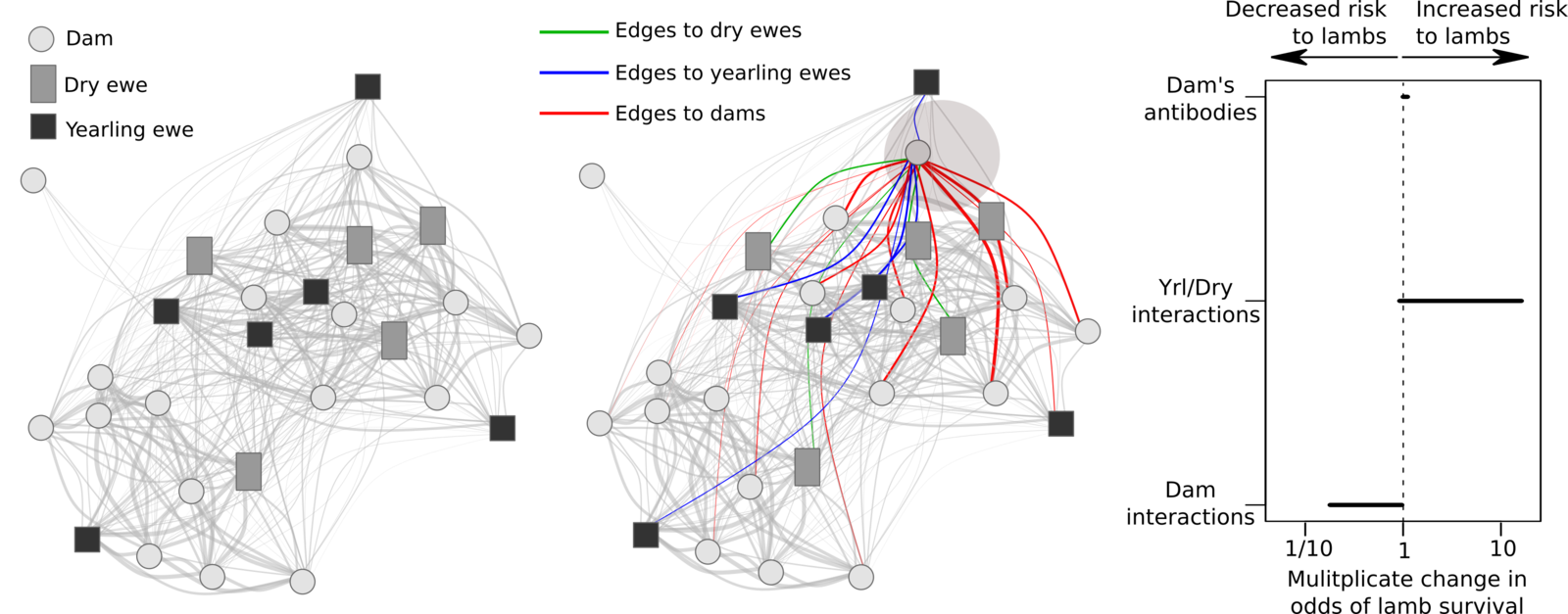
Manlove et al. in prep

Conceptualizing animal transmission networks

How do the constructions relate to one another?

How do we choose between them?

Different approaches produce different network topologies

Framework

Movement paths as triads in

(I, S, T)
(I,S,T)(I, S, T)

Ecological analyses marginalize

(I, S, T)
(I,S,T)(I, S, T)

Contacts occur at intersections in

(S, T)
(S,T)(S, T)

Network construction methods use different projections of

(I, S, T)
(I,S,T)(I, S, T)

Transmission occurs at intersections in some projection of

(I, S, T)
(I,S,T)(I, S, T)

Movement paths as triads in

(I, S, T)
(I,S,T)(I, S, T)
i \in (I^{*}: 1, ..., N)
i∈(I∗:1,...,N)i \in (I^{*}: 1, ..., N)
D_{S^{*}} \subset \mathbb{R}^{d}
DS∗⊂RdD_{S^{*}} \subset \mathbb{R}^{d}
D_{T^{*}} \in \text{animal's lifetime}
DT∗∈animal's lifetimeD_{T^{*}} \in \text{animal's lifetime}
(i, s, t) \sim f_{I^{*}, S^{*}, T^{*}}
(i,s,t)∼fI∗,S∗,T∗(i, s, t) \sim f_{I^{*}, S^{*}, T^{*}}

Ecological analyses marginalize

(I, S, T)
(I,S,T)(I, S, T)
Analysis Marginalized out Density function
Home-range
Spatial spread
Individual survival
Occupancy
T
TT
f_{(I, S)} = \int_{t \in D_ T}f_{(I, S, T)}dt
f(I,S)=∫t∈DTf(I,S,T)dtf_{(I, S)} = \int_{t \in D_ T}f_{(I, S, T)}dt
f_{(S, T)} = \sum_{i \in I}f_{(I, S, T)}
f(S,T)=∑i∈If(I,S,T)f_{(S, T)} = \sum_{i \in I}f_{(I, S, T)}
I
II
f_{I, T} = \int_{s \in D_S} f_{(I, S, T)}ds
fI,T=∫s∈DSf(I,S,T)dsf_{I, T} = \int_{s \in D_S} f_{(I, S, T)}ds
f_{S} = \sum_{i \in I}\int_{t \in D_T} f_{(I, S, T)}dt
fS=∑i∈I∫t∈DTf(I,S,T)dtf_{S} = \sum_{i \in I}\int_{t \in D_T} f_{(I, S, T)}dt
S
SS
I \text{ and } T
I and TI \text{ and } T

Contacts occur when

f_{(S, T)} \geq 2
f(S,T)≥2f_{(S, T)} \geq 2
f_{(S, T)} = \begin{cases} 0 & \text{No animals present at this point in (S, T).}\\ 1 & \text{One animal present.}\\ \geq 2 & \text{Two or more animals present: a contact.} \end{cases}
f(S,T)={0No animals present at this point in (S, T).1One animal present.≥2Two or more animals present: a contact.f_{(S, T)} = \begin{cases} 0 & \text{No animals present at this point in (S, T).}\\ 1 & \text{One animal present.}\\ \geq 2 & \text{Two or more animals present: a contact.} \end{cases}

Individual-specific contacts

I_1
I1I_1

with path

X_1 = \{I = I_1, S, T\}
X1={I=I1,S,T}X_1 = \{I = I_1, S, T\}
I_2
I2I_2

with path

X_2 = \{I = I_2, S, T\}
X2={I=I2,S,T}X_2 = \{I = I_2, S, T\}

Contacts between

occur at

I_1
I1I_1
I_2
I2I_2

and

X_1 \cap X_2 \in (D_S, D_T)
X1∩X2∈(DS,DT)X_1 \cap X_2 \in (D_S, D_T)

Network construction methods use different projections of

(I, S, T)
(I,S,T)(I, S, T)
Construction Nodes Edges Density for intersections
Dynamic social networks I Together in S, T
Static social network I Together in S, T
 
Home-range overlap networks I Overlapping home-ranges
Circuit-like networks S Individual movements between sites
Purely spatial networks S Spatial distance **
(I, S, T)
(I,S,T)(I, S, T)
(I, S)
(I,S)(I, S)
(I)
(I)(I)

** doesn't fit this framework very well....

(I, P)
(I,P)(I, P)

where P = all occupied cells in (S, T)

Application to network choice

Behavior pattern Description Examples Dependence in (I, S, T) Projection(s)
Territorial / spatially structured Non-overlapping home ranges wolves, prairie dogs, gerbils
Migratory Time and space are correlated Wildebeest, waterfowl, monarchs
Fission-fusion (strong bonds) Groups are stable, but mix in space and time Elephants, bison, giraffes
Fission-fusion (weak bonds) Individuals mix in space and time Elk, African buffalo None
(I, S)
(I,S)(I, S)
(S, T) \text{ or } (I, T)
(S,T) or (I,T)(S, T) \text{ or } (I, T)
(S, T)
(S,T)(S, T)
(I, S) \text{ or } (I, T)
(I,S) or (I,T)(I, S) \text{ or } (I, T)
(I, (S, T))
(I,(S,T))(I, (S, T))
I \text{ or } (S, T)
I or (S,T)I \text{ or } (S, T)
(I, S, T)
(I,S,T)(I, S, T)

In progress

Simulating animal movements and epidemics with varying

1. sociality

2. spatial preference

3. diffusion rate

across gradient of environmental : direct transmission

 

Building social, home-range, spatial networks

 

Simulating transmission on constructed networks

 

Measuring bias in predicted epidemic size and realized

          under various network projections

R_{0}
R0R_{0}
Made with Slides.com