Mathematical models of disease transmission

www.slides.com/keziamanlove/epimath

Who studies disease transmission, and how?

www.slides.com/keziamanlove/epimath

Olaf Hajek, nytimes

Contributing Disciplines

Within-host

Vet/Med

Micro/Immunol

"Omics"

Between- Host

Eco/Evo

Demography

Geographers

 

Prediction

Applied math

Statistics

Where do papers on non-linear aspects of disease transmission get published?

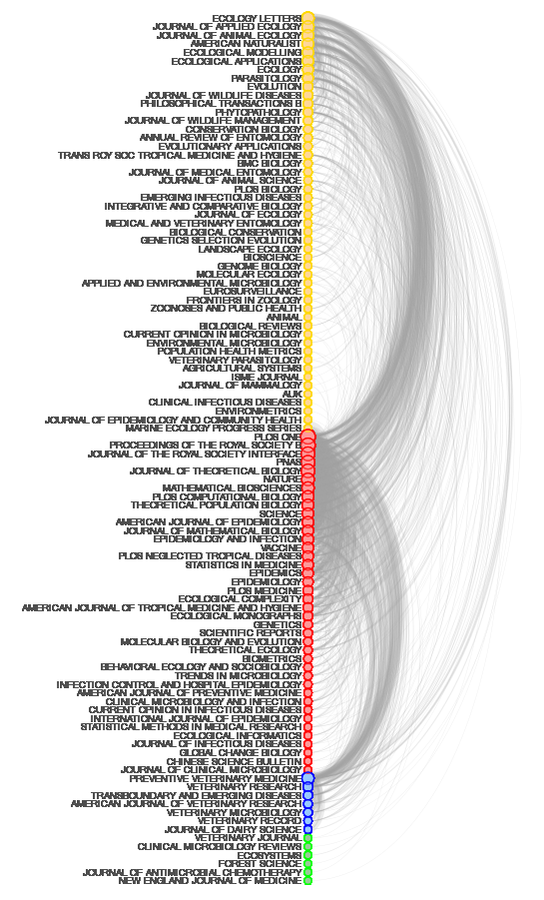
Where do papers on non-linear aspects of disease transmission get published?

K. Manlove et al., in prep

Ecology

Human Epi / Math

Vet

K. Manlove et al., in prep

Math. Biosci

PLoS Comp Biol

J Theor Biol

Theor Pop Biol

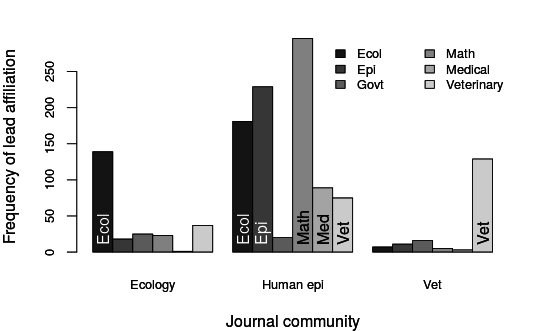
Where do papers on non-linear aspects of disease transmission get published?

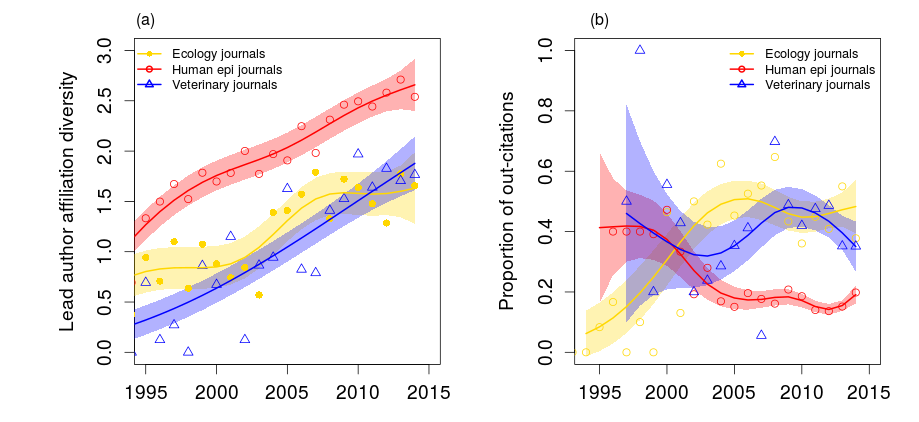
K. Manlove et al., in prep

Math/Epi
 Interface

History

Epi is not physics

Constraint # 1: Experimental ethics

 

Constraint # 2: Stochasticity is non-negligible

Consequences

1. Models remain very simple and general

 

2. Research emphasis on estimation/inference and "natural experiments"

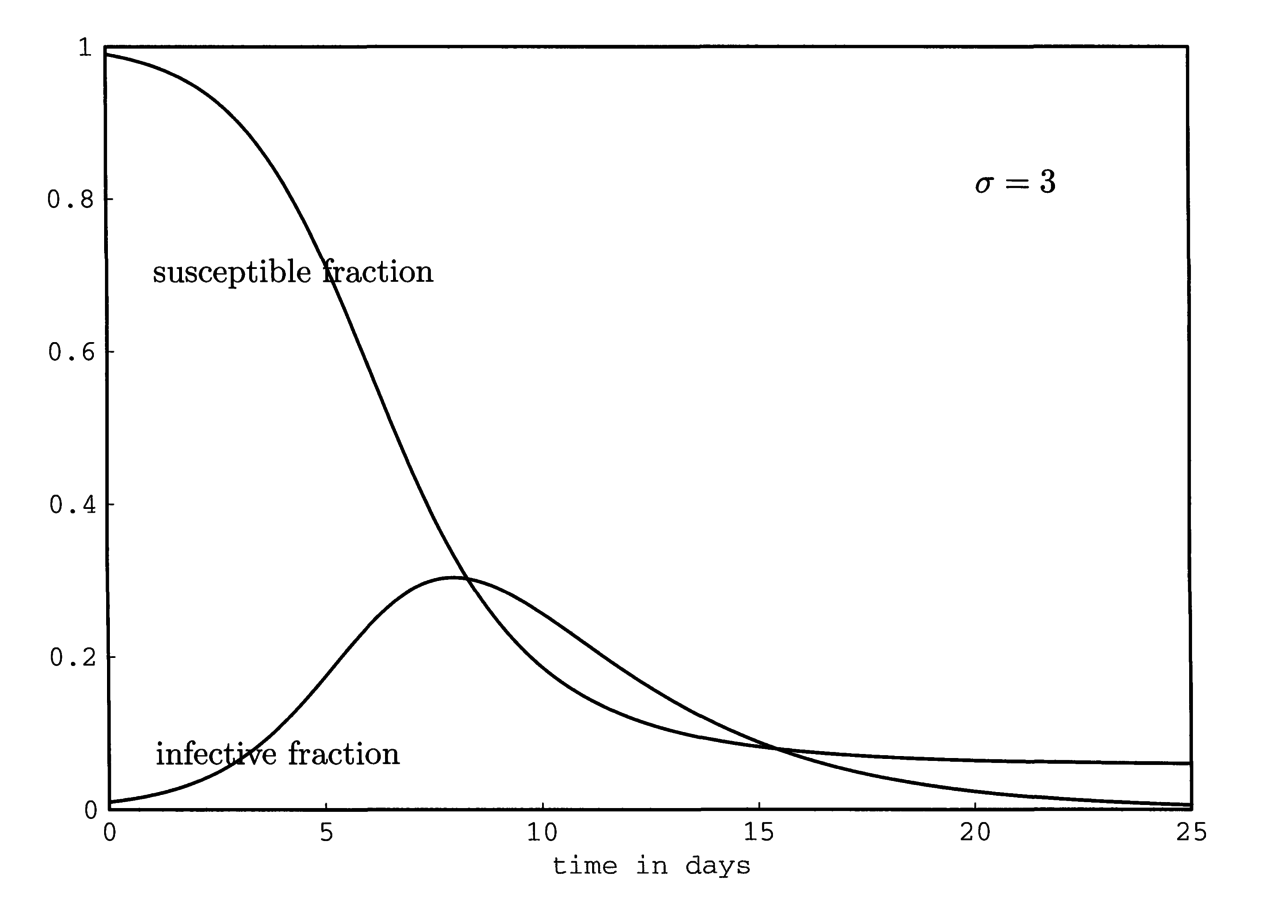
Basic between-host model

Infected/

Infectious (I)

Susceptible (S)

Recovered (R)

States

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\frac{dS}{dt} = -\beta SI - \mu S + \mu N
dSdt=−βSI−μS+μN\frac{dS}{dt} = -\beta SI - \mu S + \mu N
\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
dIdt=βSI−(γ+μ)I\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
\frac{dR}{dt} = \gamma I - \mu R
dRdt=γI−μR\frac{dR}{dt} = \gamma I - \mu R
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}

Framework 1: Differential equations

Framework 2: Stochastic (Markov) process

S I R (D)
S
I
R
(D)
1 - \beta SI - \mu
1−βSI−μ1 - \beta SI - \mu
\beta SI
βSI\beta SI
0
00

State at t + 1

State at t

0
00
1 - \gamma - \mu
1−γ−μ1 - \gamma - \mu
\gamma
γ\gamma
0
00
0
00
1 - \mu
1−μ1 - \mu
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
0
00
0
00
0
00
1
11

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}
\text{Transmission} = \text{(host contact rate)} \times \text{P(contact with infected)}
Transmission=(host contact rate)×P(contact with infected)\text{Transmission} = \text{(host contact rate)} \times \text{P(contact with infected)}
\times \text{P(Infection given contact with I)}
×P(Infection given contact with I)\times \text{P(Infection given contact with I)}

Transmission term,

\beta SI
βSI\beta SI
\kappa
κ\kappa
\propto \frac{I}{N} \text{ or } I
∝IN or I\propto \frac{I}{N} \text{ or } I
1 - c
1−c1 - c
\beta = -\kappa\log(1 - c)
β=−κlog(1−c)\beta = -\kappa\log(1 - c)

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}
R_{0}
R0R_{0}

Basic reproductive ratio,

Expected number of additional "I"s created by a single "I" in an otherwise entirely "S" population

R_{0} = \frac{\beta}{\gamma + \mu}
R0=βγ+μR_{0} = \frac{\beta}{\gamma + \mu}
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}
R_{0}
R0R_{0}

Basic reproductive ratio,

Disease Mode of transmission
Measles airborne 12-18
Pertussis airborne / droplet 12-17
Smallpox Airborne droplet 5-7
HIV Sexual contact 2-5
SARS Airborne droplet 2-5
Influenza (1918) Airborne droplet 2-3
Ebola (2014) Bodily fluids 1.5-2.5
R_{0}
R0R_{0}
R_{0} \leq 1 \Rightarrow \text{Limited transmission and eventual fade-out}
R0≤1⇒Limited transmission and eventual fade-outR_{0} \leq 1 \Rightarrow \text{Limited transmission and eventual fade-out}
R_{0} > 1 \Rightarrow \text{Pathogen persistence}
R0>1⇒Pathogen persistenceR_{0} > 1 \Rightarrow \text{Pathogen persistence}

Transmission and host density

Does transmission scale with population density?

...also depends on spatial scale

Sometimes no.

\beta \frac{SI}{N}
βSIN\beta \frac{SI}{N}
\beta SI
βSI\beta SI

e.g., STDs

Sometimes yes.

"Density-dependent" transmission

"Frequency-dependent" transmission

aerosolized / fomite-driven transmission

Frequency- (FD) vs. Density- (DD) dependent Transmission

FD pathogens can drive the host extinct;

DD cannot.

(transmission eventually limited by too few S's)

I

S

R

Assumptions

1. Directly transmitted microparasites

 

2. Immunizing infections / life-long immunity

 

3. Well-mixed populations

 

4. Limited heterogeneity within compartments

Equilibrium Results

(Endemic disease)

Equilibria

\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
dIdt=βSI−(γ+μ)I\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}
\text{Equilibria at } I\left(\beta S - (\gamma + \mu)\right) = 0
Equilibria at I(βS−(γ+μ))=0\text{Equilibria at } I\left(\beta S - (\gamma + \mu)\right) = 0
I^{*} = 0
I∗=0I^{*} = 0
S^{*} = \frac{\gamma + \mu}{\beta} = \frac{1}{R_{0}}
S∗=γ+μβ=1R0S^{*} = \frac{\gamma + \mu}{\beta} = \frac{1}{R_{0}}

Disease-Free

Endemic

I^{*} = \frac{\mu}{\gamma}\left(1 - \frac{1}{R_{0}}\right) = \frac{\mu}{\beta}\left(R_{0} - 1\right)
I∗=μγ(1−1R0)=μβ(R0−1)I^{*} = \frac{\mu}{\gamma}\left(1 - \frac{1}{R_{0}}\right) = \frac{\mu}{\beta}\left(R_{0} - 1\right)

Herd immunity

System with vaccination rate    and basic reproductive ratio

    is dynamically identical to a system with

p
pp
R_{0}
R0R_{0}
R_{0}^{'} = (1 - p)R_{0}
R0′=(1−p)R0R_{0}^{'} = (1 - p)R_{0}

If high-enough proportion of pop is immune, pathogen will fade-out

Vaccination can manipulate       downward

R_{0}
R0R_{0}

Age-Seroprevalence and

R_{0}
R0R_{0}

Seroprevalence: Proportion of population that has antibodies

to pathogen X (cumulative exposure; R + part of I)

For fully immunizing pathogens, Recovery is an absorbing state

A \approx \frac{1}{\mu(R_{0} - 1)}
A≈1μ(R0−1)A \approx \frac{1}{\mu(R_{0} - 1)}

Age at first infection (A) depends on infectiousness of pathogen (     ), and host life-span (   )

R_0
R0R_0
\mu
μ\mu
A \approx \frac{1}{\mu(R_{0} - 1)}
A≈1μ(R0−1)A \approx \frac{1}{\mu(R_{0} - 1)}

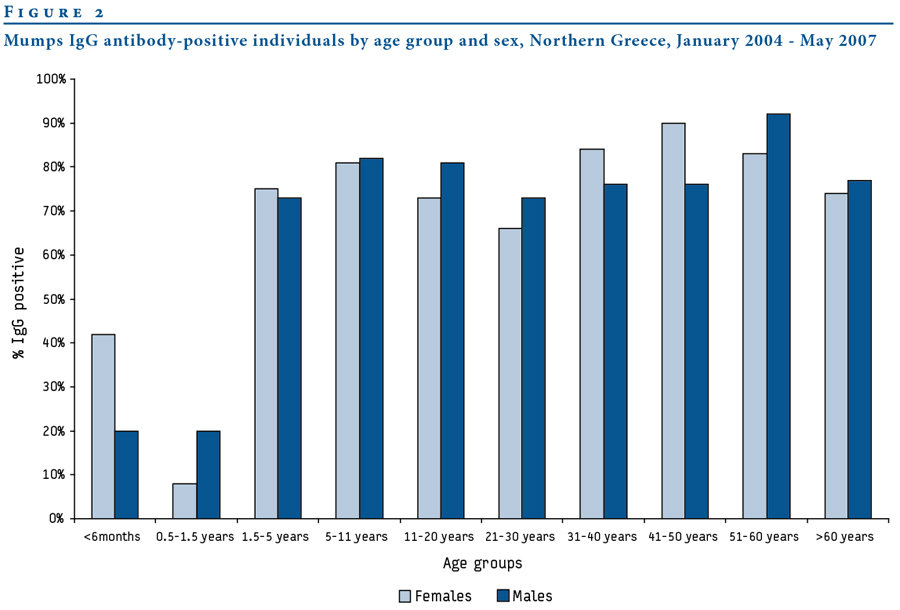
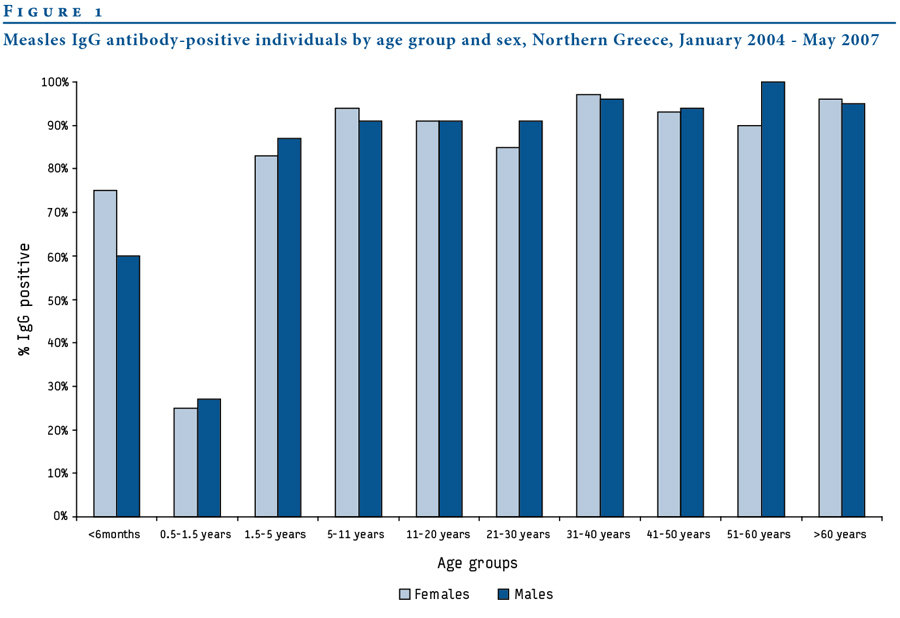
Fylaktou et al., Eurosurveillance, 2008

Measles

Mumps

R_{0}
R0R_{0}
R_{0}
R0R_{0}

12-18

4-7

Measles and Whooping cough

Assume constant pop size

Start with 3-D system

R(t) = N - S(t) - I(t)
R(t)=N−S(t)−I(t)R(t) = N - S(t) - I(t)

So, system reduces to 2-D

\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\lambda = \text{Force of infection}
λ=Force of infection\lambda = \text{Force of infection}
\nu = \text{Recovery rate}
ν=Recovery rate\nu = \text{Recovery rate}
\frac{dS}{dt} = -\beta SI - \mu S + \mu N
dSdt=−βSI−μS+μN\frac{dS}{dt} = -\beta SI - \mu S + \mu N
\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
dIdt=βSI−(γ+μ)I\frac{dI}{dt} = \beta SI - \left(\gamma + \mu\right) I
\frac{dR}{dt} = \gamma I - \mu R
dRdt=γI−μR\frac{dR}{dt} = \gamma I - \mu R
\frac{dS}{dt} = \mu - (\mu + \lambda(t))S(t)
dSdt=μ−(μ+λ(t))S(t)\frac{dS}{dt} = \mu - (\mu + \lambda(t))S(t)
\frac{d\lambda}{dt} = (\nu + \mu)\lambda(t)(R_{0}S(t) - 1)
dλdt=(ν+μ)λ(t)(R0S(t)−1)\frac{d\lambda}{dt} = (\nu + \mu)\lambda(t)(R_{0}S(t) - 1)

Damped Oscillator

\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\lambda = \text{Force of infection}
λ=Force of infection\lambda = \text{Force of infection}
\nu = \text{Recovery rate}
ν=Recovery rate\nu = \text{Recovery rate}
T \approx 2\pi\frac{L(\frac{1}{\nu} + \frac{1}{\sigma})}{R_{0} - 1}^{1/2}
T≈2πL(1ν+1σ)R0−11/2T \approx 2\pi\frac{L(\frac{1}{\nu} + \frac{1}{\sigma})}{R_{0} - 1}^{1/2}
L = \text{Host life expectancy}
L=Host life expectancyL = \text{Host life expectancy}
\sigma = \text{Incubation rate}
σ=Incubation rate\sigma = \text{Incubation rate}

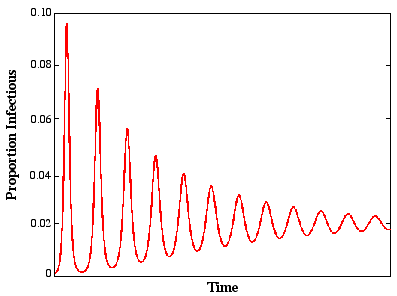
Does this match reality?

Measles Fade-outs and Cycles

1. Critical community size:

Measles will "fade-out" in small pops, but not large ones

Continuous influx of susceptibles through births

2. Correlation between epidemic period and community size

Biennial periods in large communities; waiting time increases in smaller towns

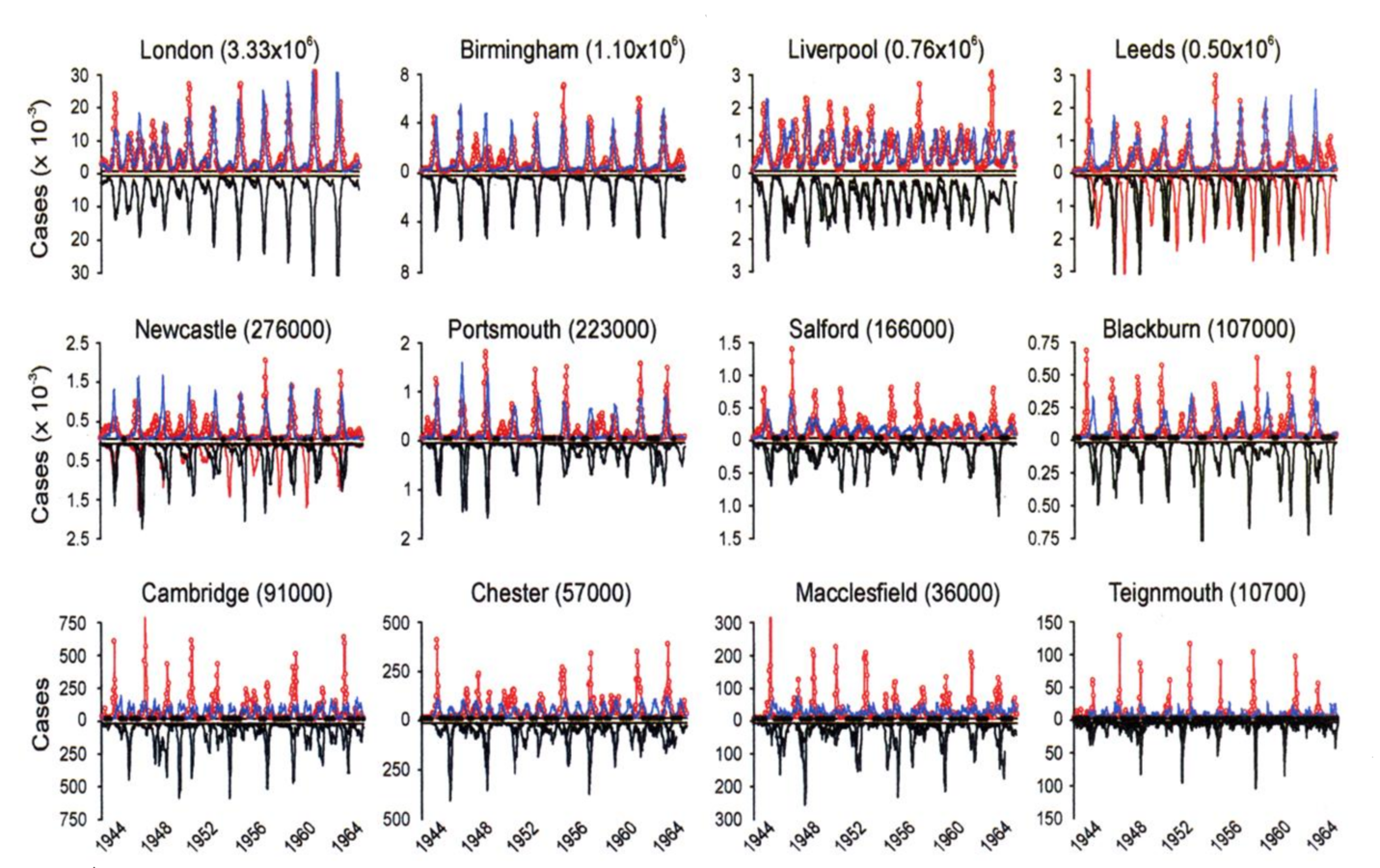
Pre-Vaccination Measles (UK)

Grenfell et al., 2001, Ecol Monogr

Don't look very damped....

How to explain "stable" oscillations?

1. Seasonal forcing from aggregation of school children

Pre-schoolers distinct from school-age peers

Problem: Too much fade-out

2. Realistic age structure

Pre-schoolers provide out-of-school contacts to get measles through trough

Added bonus: Sinusoidal forcing gets you chaos!

How transportable is that model?

1. Does model hold under varied birth pulse?

3. Does model hold for other childhood diseases?

2. Does model hold under vaccination?

Rohani et al., 2002, Am Nat

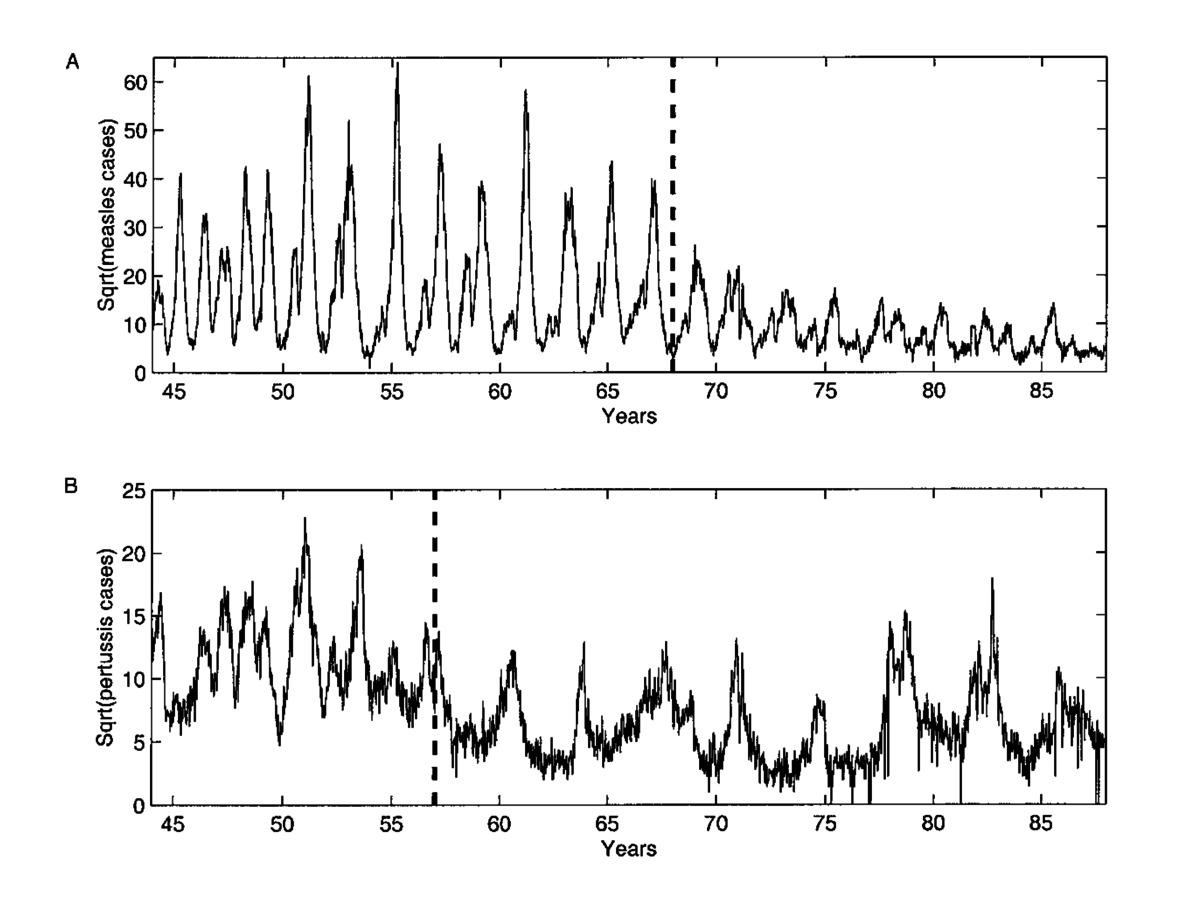
Measles in the UK

Post-WWII baby boom

Classic biennical cycles

Vaccination-era

Keeling, Rohani, Grenfell (2001) Physica D

Baby boom

Model re-creates observed change in measles period

over varied birth pulse and vaccination

Rohani et al., 2002, Am Nat

Measles in the UK

Whooping cough

Annual outbreaks + 2-year epidemics

Post-vaccination 4-year cycles

Measles

Whooping Cough

In simulation, if you shift some S's and I's into R, system barely notices

System responds pretty dramatically if you move some S's and I's into R

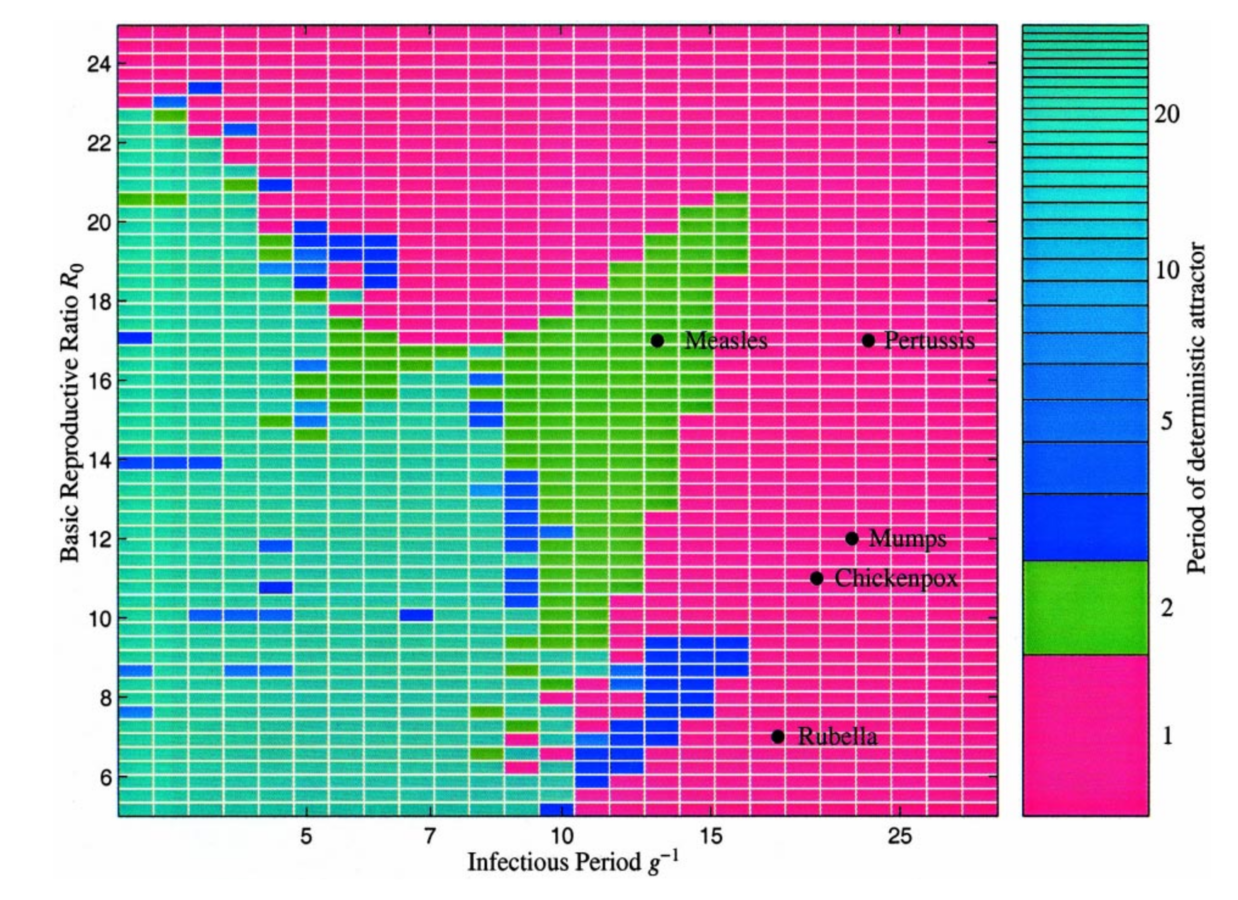
Do measles and whooping cough attractors differ in stability?

SIR models for measles and whooping cough

Do measles and whooping cough attractors differ in stability?

Compared dominant global Lyapunov exponents

Both systems have negative global Lyapunov exponents

=> stable, periodic attractor in both cases

(whooping cough slightly more negative than measles)

Both systems have similar local Lyapunov exponents

"Vaccination-like" perturbations (move some I's to R) have different impacts

Measles: transients return to the biennial attractor (so, robust)

Whooping cough: same magnitude of perturbation move trajectories off the attractor; you get multiyear periods of transient dynamics (so, sensitive)

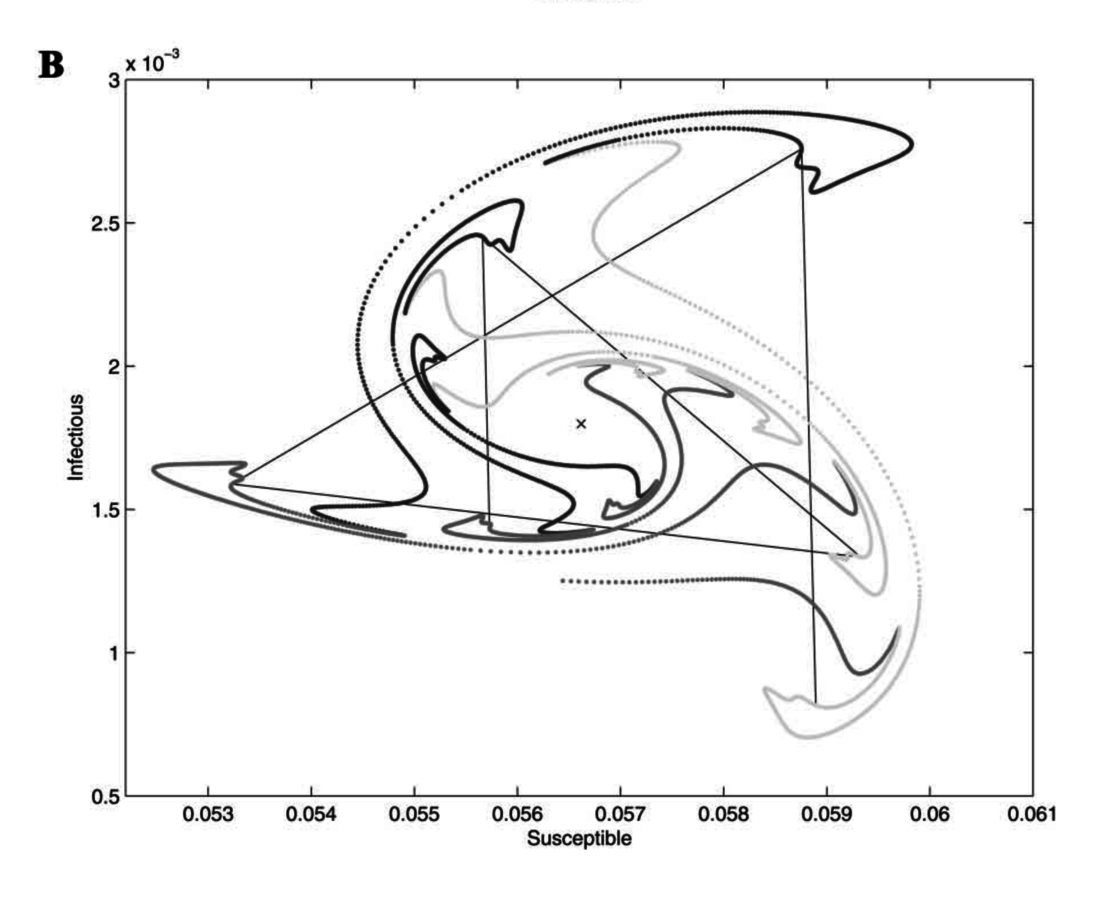
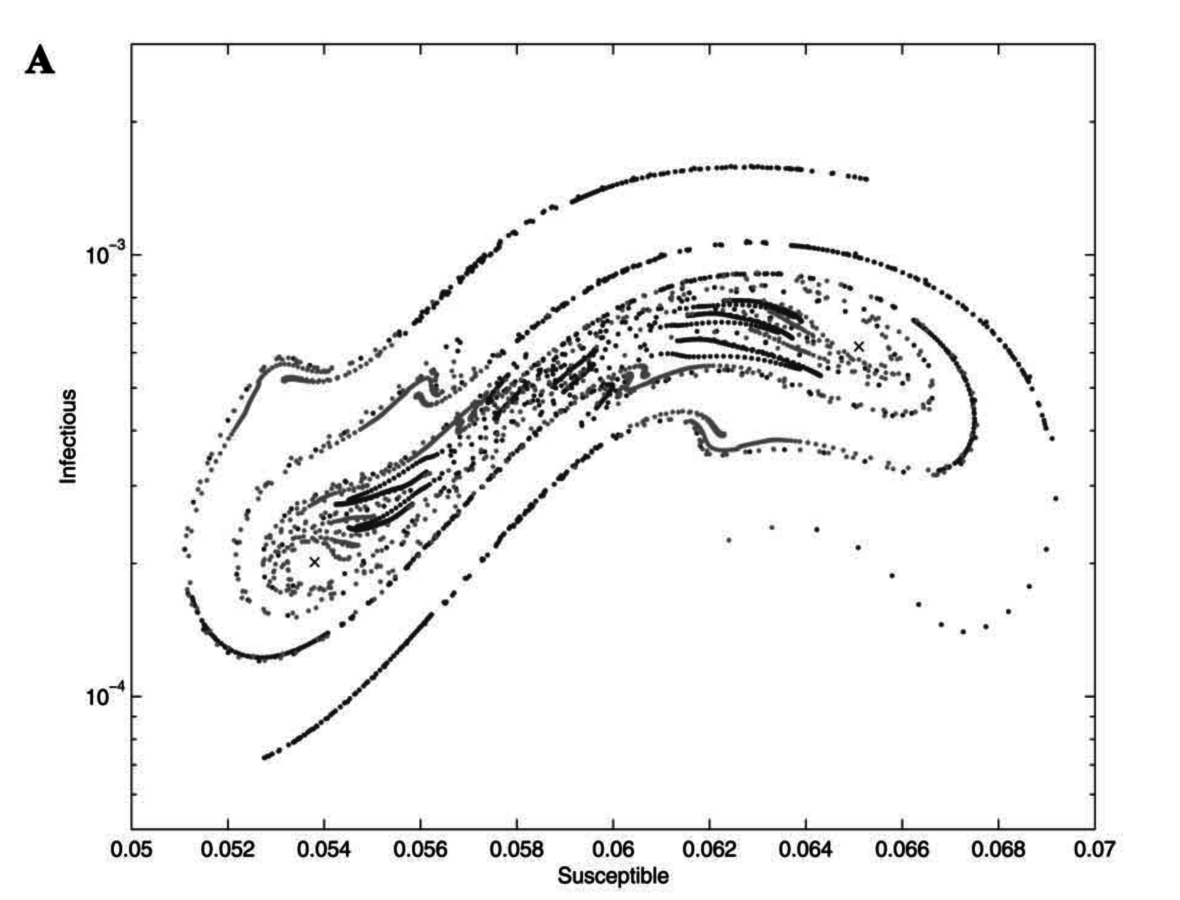
Measles

Whooping cough

Invasion orbits (very small I; almost all S)

Rohani et al., 2002, Am Nat

Whooping cough is really weird.

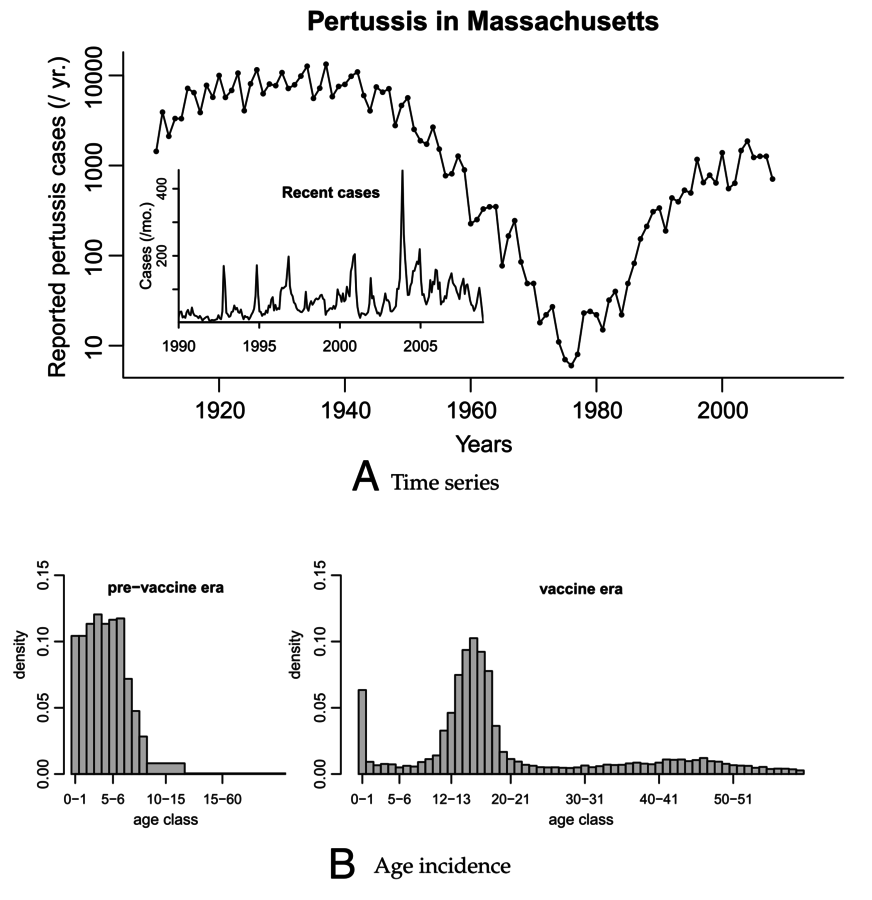
Lavine, King, Bjornstad (2011) PNAS

I

S

R

\beta SI
βSI\beta SI
\gamma
γ\gamma
\mu
μ\mu
\mu
μ\mu
\mu
μ\mu
\mu = \text{Natural mortality}
μ=Natural mortality\mu = \text{Natural mortality}
\beta = \text{Transmission rate}
β=Transmission rate\beta = \text{Transmission rate}
\gamma = \text{Recovery rate}
γ=Recovery rate\gamma = \text{Recovery rate}

W

(R is no longer an absorbing state)

\kappa \times \beta SI
κ×βSI\kappa \times \beta SI
\kappa = \text{Ease of boosting}
κ=Ease of boosting\kappa = \text{Ease of boosting}

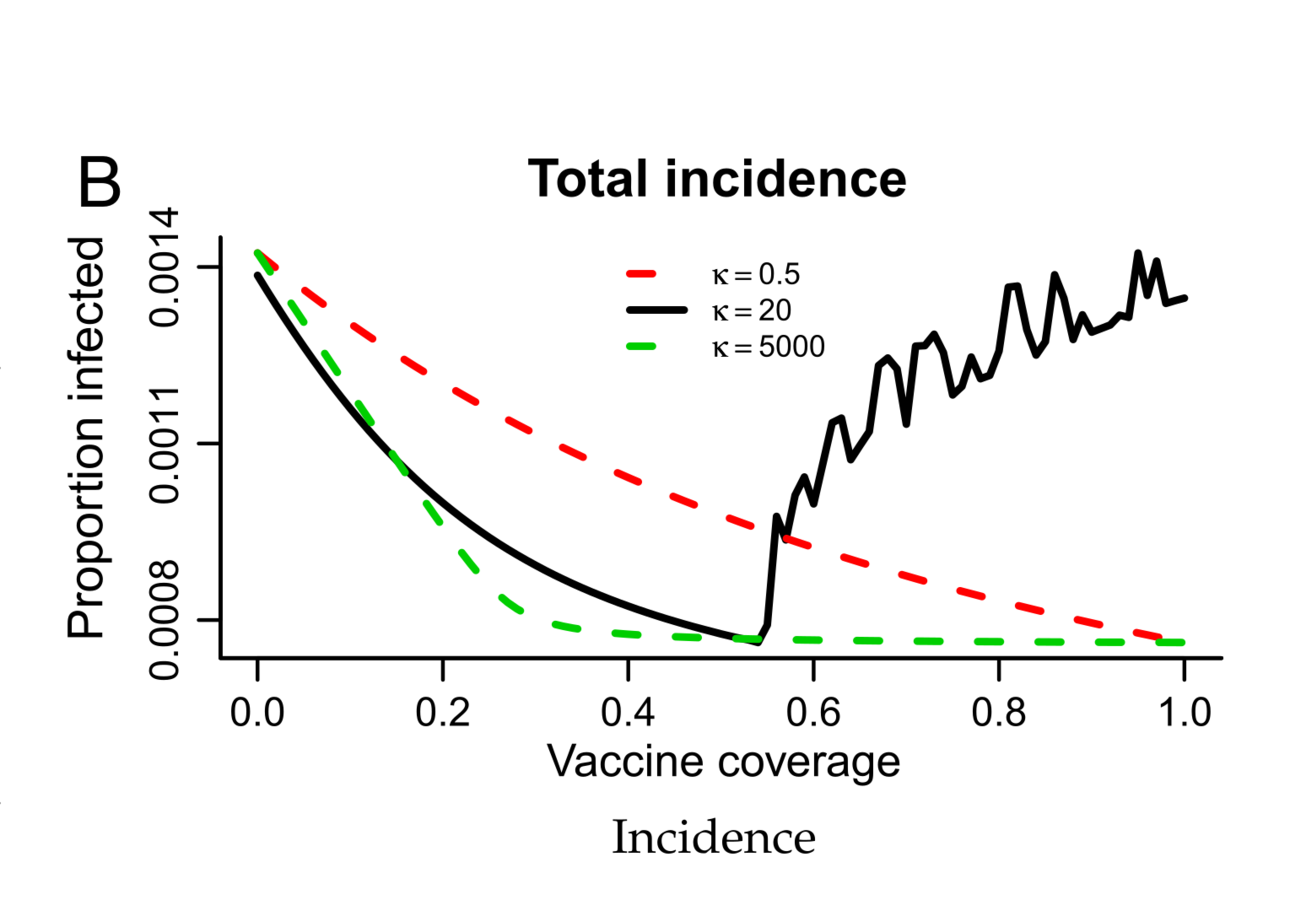
Why is whooping cough such a mess?

Hypothesis: Boosting through re-exposure

Lavine, King, Bjornstad (2011) PNAS

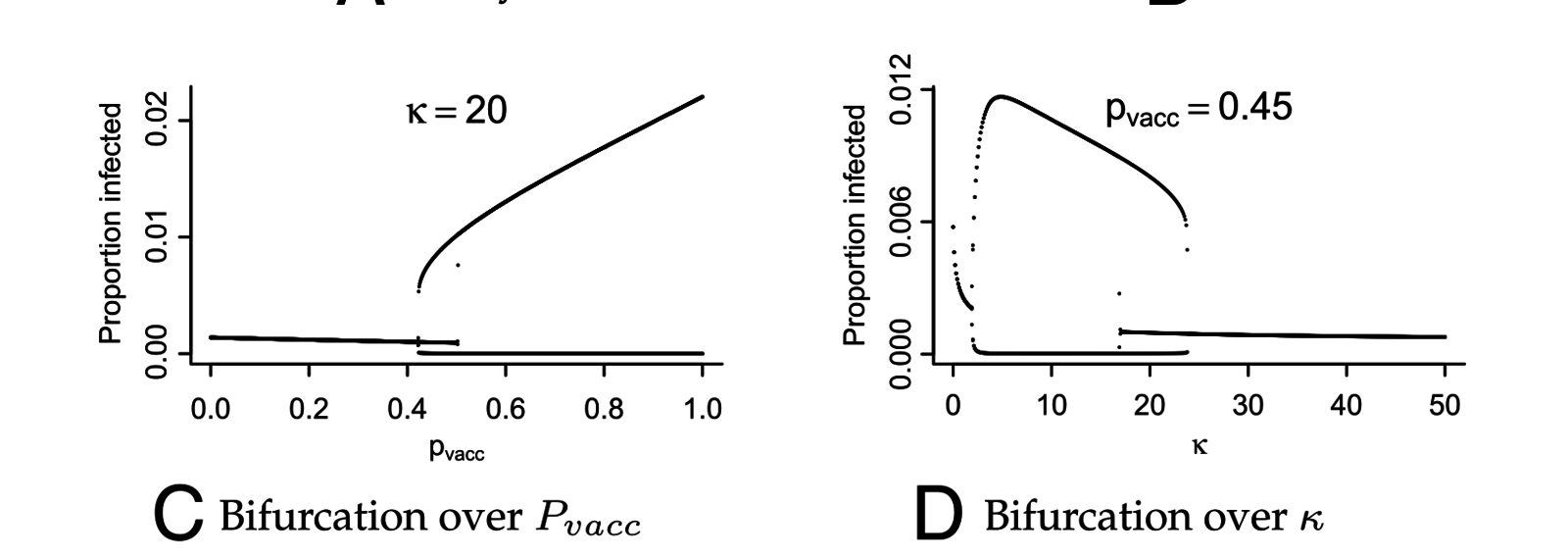
Lavine, King, Bjornstad (2011) PNAS

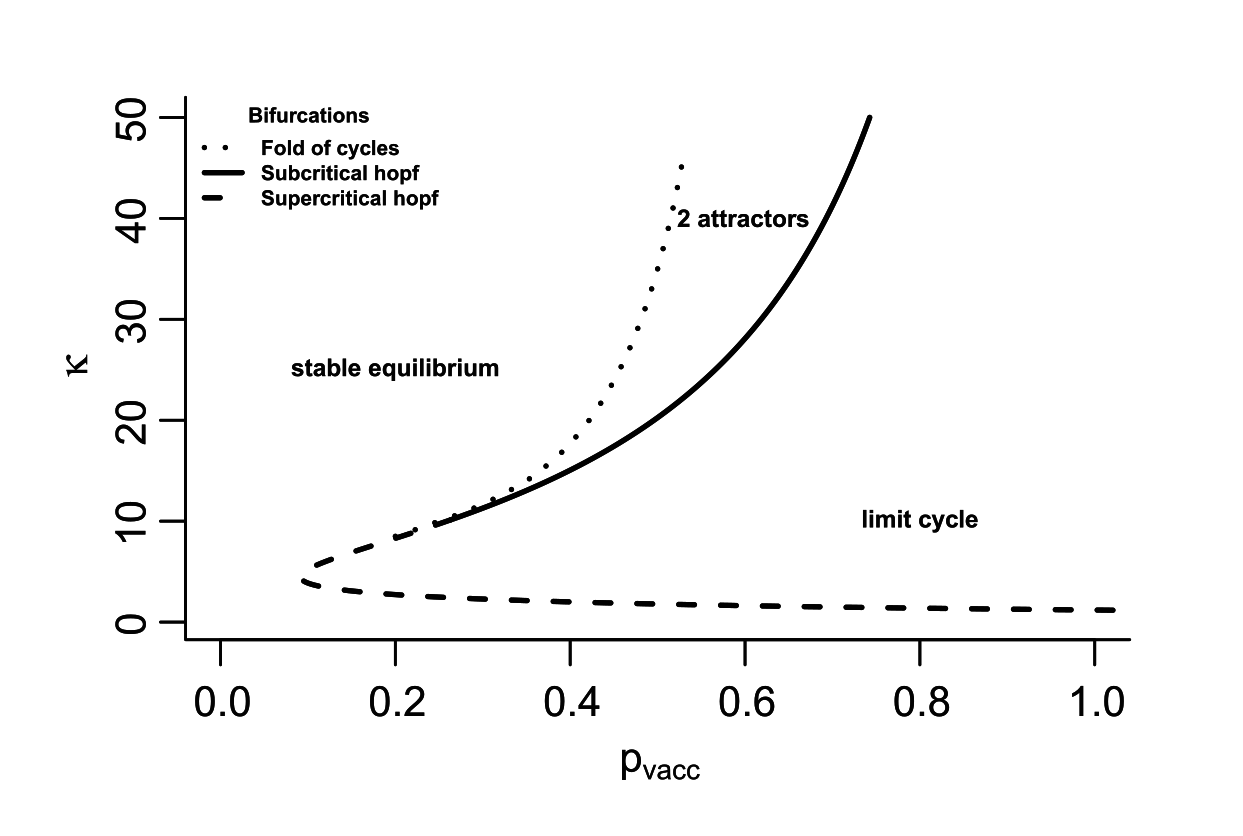
So, whooping cough boosting vaccinations for teenagers

Inference

State-space models

Approximate Bayesian Computation ("ABC")

Partially observed Markov Process Models

Current research foci

Super-spreaders

Basic tenet:

I is not homogeneous

SARS motivated

A few individuals apparently accounted for almost all of the transmission

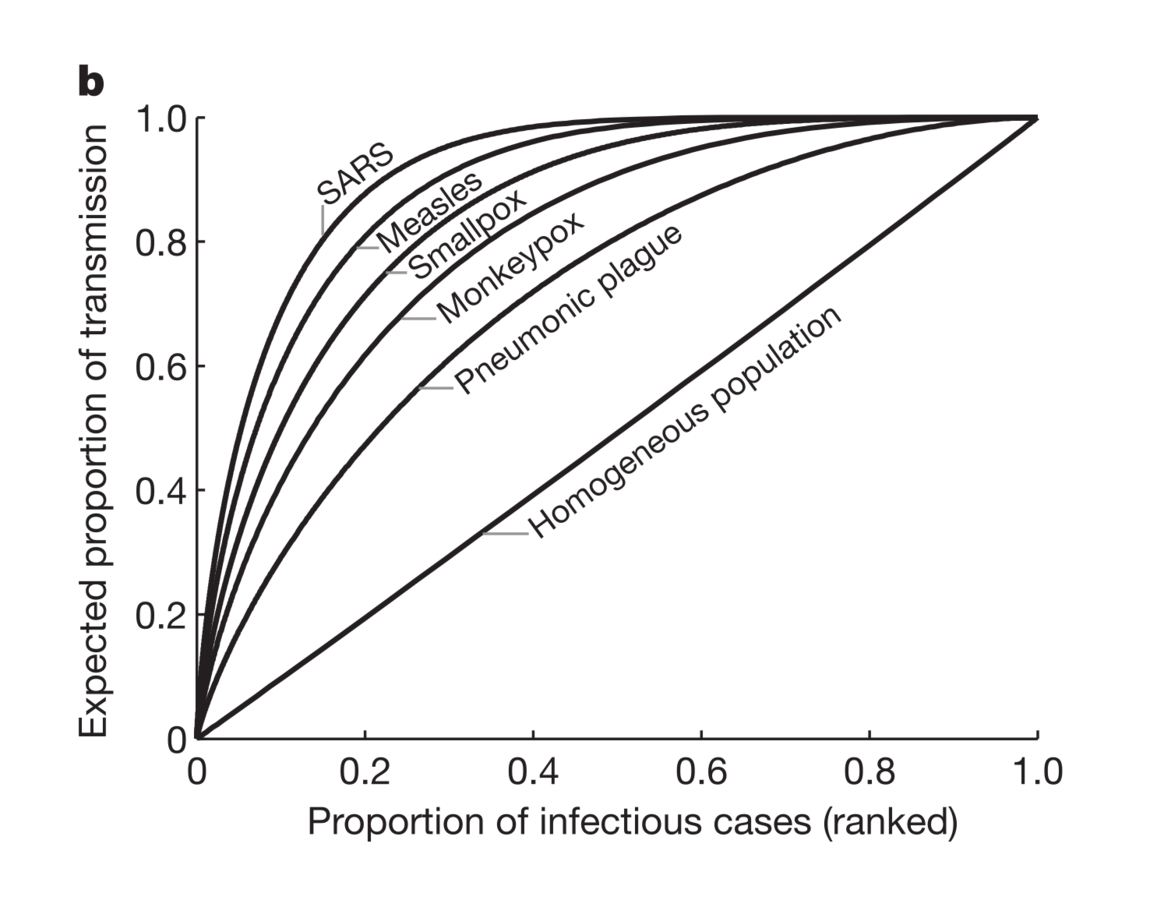
Lloyd-Smith et al., Nature, 2005

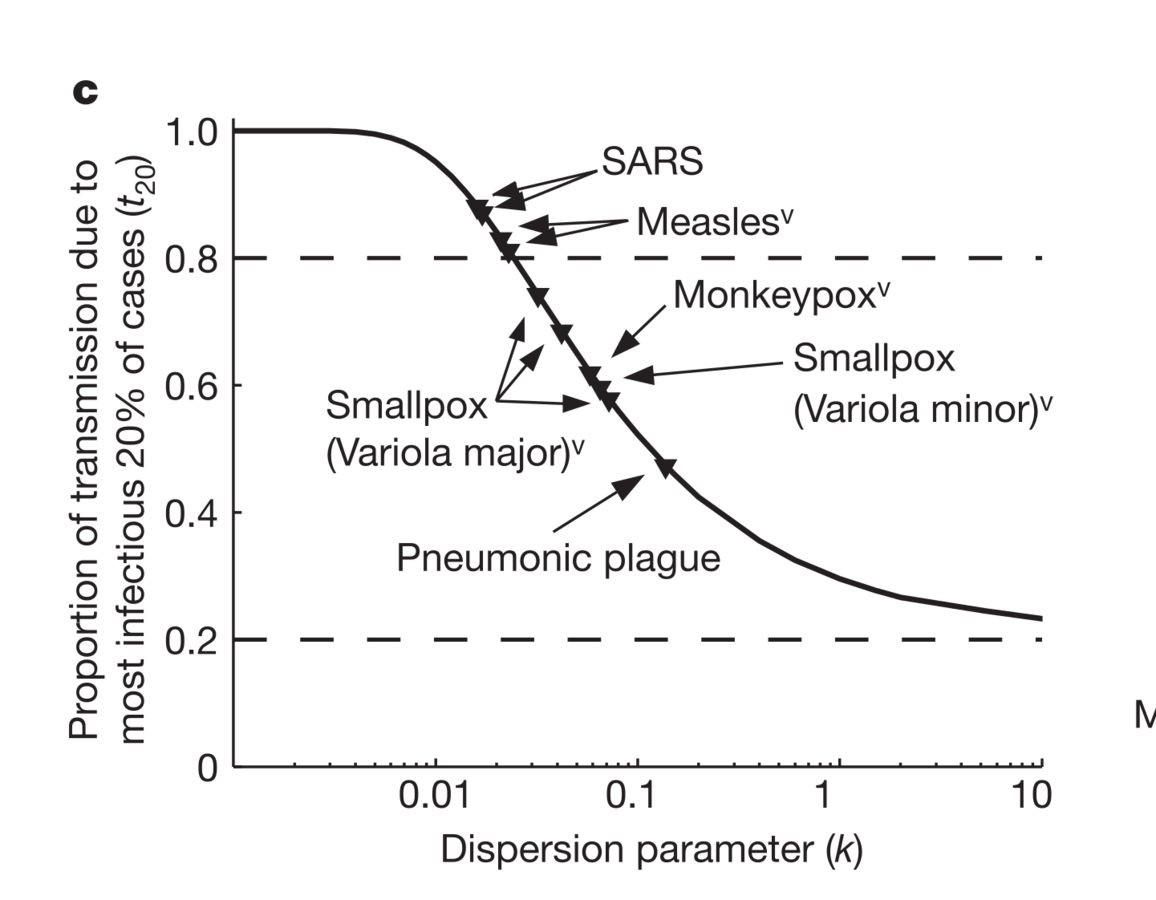
Focus: dispersion in # cases generated

Z = \text{RV representing number of } 2^{0} \text{ cases produced by a particular I}
Z=RV representing number of 20 cases produced by a particular IZ = \text{RV representing number of } 2^{0} \text{ cases produced by a particular I}
\nu = R_{0} \Rightarrow Z \sim Pois(R_{0})
ν=R0⇒Z∼Pois(R0)\nu = R_{0} \Rightarrow Z \sim Pois(R_{0})
\nu \sim Exp() \Rightarrow Z \sim Geometric(R_{0})
ν∼Exp()⇒Z∼Geometric(R0)\nu \sim Exp() \Rightarrow Z \sim Geometric(R_{0})
\nu \sim Gamma\left(R_{0}, \kappa \right) \Rightarrow Z \sim \text{Neg Bin}(R_{0}, \kappa)
ν∼Gamma(R0,κ)⇒Z∼Neg Bin(R0,κ)\nu \sim Gamma\left(R_{0}, \kappa \right) \Rightarrow Z \sim \text{Neg Bin}(R_{0}, \kappa)
\nu = \text{"individual reproductive number"} \sim \left(\mu = R_{0}\right)
ν="individual reproductive number"∼(μ=R0)\nu = \text{"individual reproductive number"} \sim \left(\mu = R_{0}\right)
\text{Var(Z)} = \frac{R_{0}}{1 + \frac{R_{0}}{\kappa}}
Var(Z)=R01+R0κ\text{Var(Z)} = \frac{R_{0}}{1 + \frac{R_{0}}{\kappa}}

Increased dispersion in I led to more explosive, and rarer, epidemics

Cross-scale models

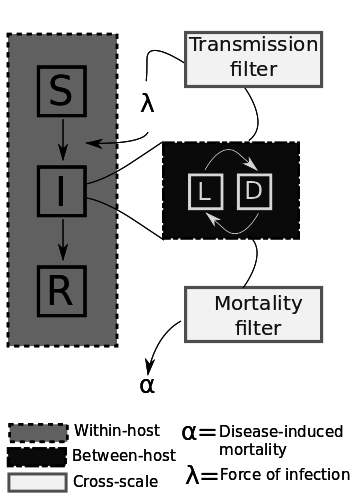
Two Questions

1. What happens in the host?

2. How do we map?

Two (non-mutually-exclusive) within-host models

Antigen-driven dynamics

  • Predator-prey between immune system (D) and pathogen(L)

 

 

Network regulation model

  • Internal feedbacks control host's immune response
\frac{dL(\tau)}{d\tau} = \rho L(\tau) - \frac{\nu L(\tau)^{2}D(\tau)}{\psi^{2} + L(\tau)^{2}}
dL(τ)dτ=ρL(τ)−νL(τ)2D(τ)ψ2+L(τ)2\frac{dL(\tau)}{d\tau} = \rho L(\tau) - \frac{\nu L(\tau)^{2}D(\tau)}{\psi^{2} + L(\tau)^{2}}
\frac{dD(\tau)}{d\tau} = D(\tau)\frac{\phi\nu L(\tau)^{2}}{\psi^{2} + L(\tau)^{2}} - \epsilon D(\tau)
dD(τ)dτ=D(τ)ϕνL(τ)2ψ2+L(τ)2−ϵD(τ)\frac{dD(\tau)}{d\tau} = D(\tau)\frac{\phi\nu L(\tau)^{2}}{\psi^{2} + L(\tau)^{2}} - \epsilon D(\tau)

Holling Type III Functional response

Cross-Scale Considerations

Have to model age-of-infection for all I's

\Rightarrow{PDEs}
⇒PDEs\Rightarrow{PDEs}
\frac{dS(t)}{dt} = \theta - \mu S(t) \int_{0}^{\infty}\beta(a)I(a, t)da
dS(t)dt=θ−μS(t)∫0∞β(a)I(a,t)da\frac{dS(t)}{dt} = \theta - \mu S(t) \int_{0}^{\infty}\beta(a)I(a, t)da
\frac{\partial I(a, t)}{\partial t} = -\frac{\partial I(a, t)}{\partial t} - \alpha(a)I(a, t)
∂I(a,t)∂t=−∂I(a,t)∂t−α(a)I(a,t)\frac{\partial I(a, t)}{\partial t} = -\frac{\partial I(a, t)}{\partial t} - \alpha(a)I(a, t)
I(0, t) = S(t) \int_{0}^{\infty}\beta(a)I(a, t)da
I(0,t)=S(t)∫0∞β(a)I(a,t)daI(0, t) = S(t) \int_{0}^{\infty}\beta(a)I(a, t)da
\theta = \text{birth rate}
θ=birth rate\theta = \text{birth rate}
\mu = \text{host mortality rate}
μ=host mortality rate\mu = \text{host mortality rate}
\alpha = \text{loss rate of individuals from I}
α=loss rate of individuals from I\alpha = \text{loss rate of individuals from I}

Within-host outcomes of pathogen invasion

1. Acute infection, followed by clearance

  • Measles, Mumps, Rubella, Variola (Pox), Influenza

2. Recurrent disease (e.g., repeated growth and decay of pathogen population within the host)

  • Herpes symplex virus, HPV, HIV, Tuberculosis

3. Inapparent / dormant infections (no symptoms; pathogen isn't detectable)

  • Whooping cough (??)

 

4. Subclinical infections (no symptoms; pathogen is detectable)

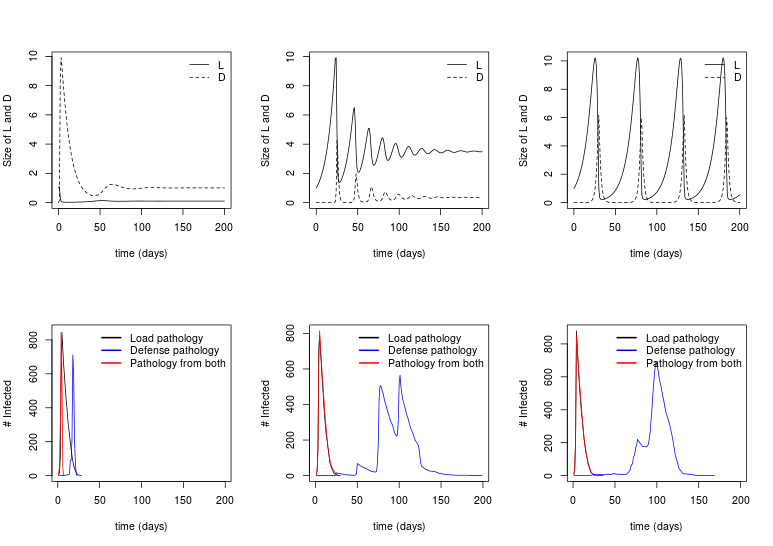
Manlove, Cross, Plowright in prep.

Pathogen clearance

Pathogen persistence

Pathogen cycling

Consider 3 maps from within- to between

1. Transmission / mortality depend only on Load (L)

2. Transmission / mortality depend only on Defense (D)

3. Trans / mort depend on some combination of L and D

Manlove, Cross, Plowright in prep.

Pathogen clearance

Pathogen persistence

Pathogen cycling

Social network theory and contacts

Wrap-up

1. Epidemiological modeling is fundamentally x-disciplinary

2. Historic challenge: identifying deterministic vs. stochastic aspects of system

3. Current mathematical foci:

  • x-scale modeling
  • spatial spread

4. Current statistical foci:

  • Non-linear series data (esp. hierarchical modeling structures)
  • Spatiotemporal data analysis
  • Hierarchical inferential schemes

Questions?

www.slides.com/keziamanlove/epimath

Made with Slides.com